Uniswap V3 中的 TickMath getSqrtRatioAtTick 函数是如何工作的

Tickmath getSqrtRatioAtTick

本文解释了 Uniswap V3 TickMath 库中的 getSqrtRatioAtTick() 函数是如何工作的。getSqrtRatioAtTick() 函数接受一个 tick 索引，并返回该 tick 处的平方根价格，格式为 Q64.96 q-number。该函数计算：

$sqrtPriceX96= \sqrt {1.0001^i}⋅2^{96}$

其中 i 是 tick 索引。以下是该函数的截图：

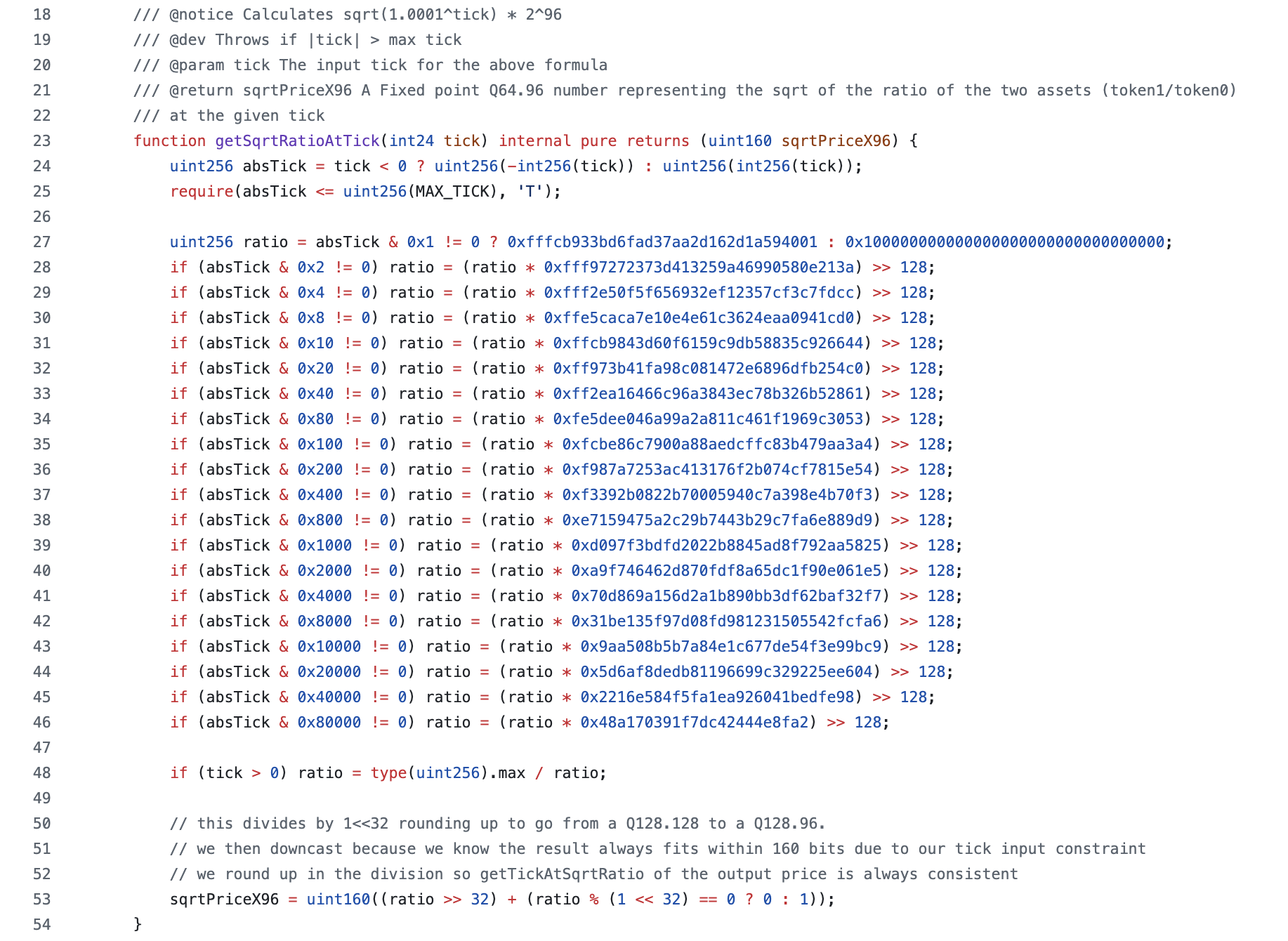
本教程假定读者已经理解了我们对平方和乘算法的处理，getSqrtRatioAtTick() 依赖于该算法。我们在此经常引用该教程中的概念，因此我们建议读者首先阅读该文章。

getSqrtPriceRatioAtTick 概述

该函数执行以下步骤：

1. 使用代码 uint256 absTick = tick < 0 ? uint256(-int256(tick)) : uint256(int256(tick)); 计算 tick 的绝对值。
2. 检查 tick 是否在最小和最大 tick 的范围内，如果超出范围则恢复：require(absTick <= uint256(MAX_TICK), 'T');。
3. 使用平方和乘法计算 $ \sqrt {1.0001^{−|i|}} $ 作为 Q128.128 number。
4. 如果原始 tick 为正，则计算 $ 1/ \sqrt {1.0001^{−|i|}} $
5. 使用 >> 32 将 Q128.128 number 转换为 Q64.96 number

以下是代码中概述的步骤：

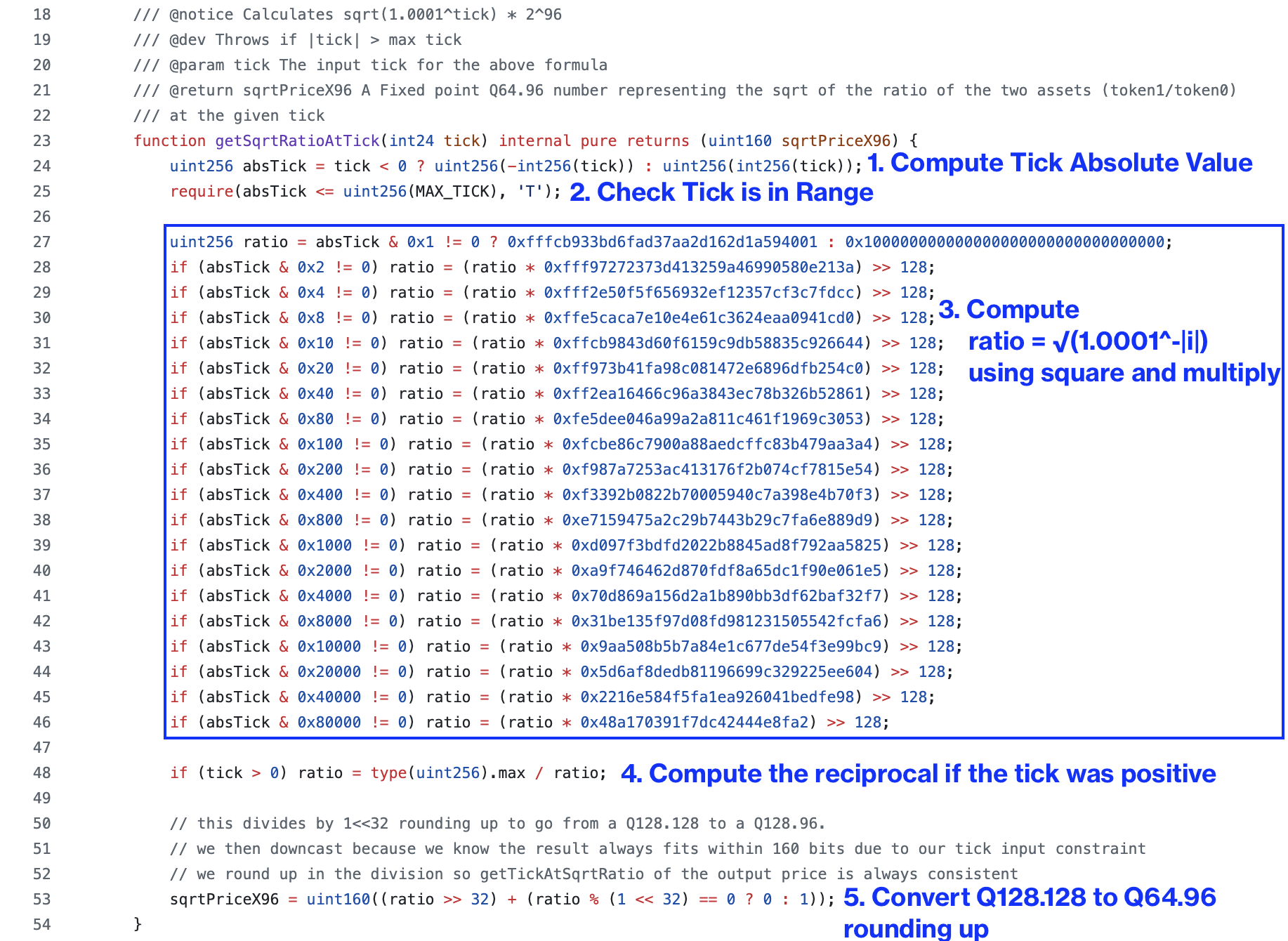
第 1/5 部分：为什么 Uniswap V3 计算绝对值 tick

为什么 Uniswap V3 计算绝对值 tick，，即 $ \sqrt {1.0001^{−|i|}} $, 函数中的第一行代码计算 tick 的绝对值：

uint256 absTick = tick < 0 ? uint256(-int256(tick)) : uint256(int256(tick));

Tick 索引可以是正数也可以是负数。为了避免分别处理这两种情况，getSqrtRatioAtTick() 的平方和乘法部分仅计算负数 tick。如果原始 tick 为正数，则平方和乘法算法的结果计算倒数。

例如，如果原始 tick 为正 5，则该算法计算 -5 的 tick：

$ratio=\sqrt {1.0001^{−5}}$

然后计算倒数：

$ {1 / ratio}$

观察到一般情况下：

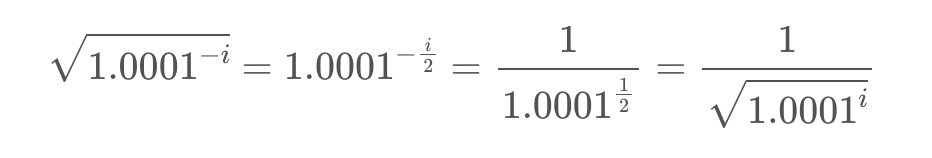因此，该函数首先计算： 然后，如果 tick 最初为正数，它会通过返回倒数来反转答案：

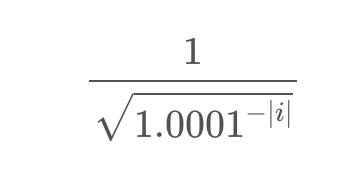
如果 tick 最初为负数，则代码不计算倒数。

第 2/5 部分：检查 tick 是否在范围内

函数中的第二行代码是不言自明的：

require(absTick <= uint256(MAX_TICK), 'T');

Max tick 是文件中的一个常量 887272，我们在关于 Tick 限制的文章中推导出了它。 我们不需要检查 tick 是否小于 MIN_TICK，因为我们计算了 tick 的绝对值，所以 absTick 不可能是负数。

第 3/5 部分：使用平方和乘法计算价格

在本节中，我们将展示该函数如何使用平方和乘算法并推导出函数中的大常量。

用于计算价格的变量是 ratio，但返回的变量是 sqrtPriceX96。

以下是使用平方和乘法的函数的相关部分：

uint256 ratio = absTick & 0x1 != 0 ? 0xfffcb933bd6fad37aa2d162d1a594001 : 0x100000000000000000000000000000000;
if (absTick & 0x2 != 0) ratio = (ratio * 0xfff97272373d413259a46990580e213a) >> 128;
if (absTick & 0x4 != 0) ratio = (ratio * 0xfff2e50f5f656932ef12357cf3c7fdcc) >> 128;
if (absTick & 0x8 != 0) ratio = (ratio * 0xffe5caca7e10e4e61c3624eaa0941cd0) >> 128;
if (absTick & 0x10 != 0) ratio = (ratio * 0xffcb9843d60f6159c9db58835c926644) >> 128;
if (absTick & 0x20 != 0) ratio = (ratio * 0xff973b41fa98c081472e6896dfb254c0) >> 128;
if (absTick & 0x40 != 0) ratio = (ratio * 0xff2ea16466c96a3843ec78b326b52861) >> 128;
if (absTick & 0x80 != 0) ratio = (ratio * 0xfe5dee046a99a2a811c461f1969c3053) >> 128;
if (absTick & 0x100 != 0) ratio = (ratio * 0xfcbe86c7900a88aedcffc83b479aa3a4) >> 128;
if (absTick & 0x200 != 0) ratio = (ratio * 0xf987a7253ac413176f2b074cf7815e54) >> 128;
if (absTick & 0x400 != 0) ratio = (ratio * 0xf3392b0822b70005940c7a398e4b70f3) >> 128;
if (absTick & 0x800 != 0) ratio = (ratio * 0xe7159475a2c29b7443b29c7fa6e889d9) >> 128;
if (absTick & 0x1000 != 0) ratio = (ratio * 0xd097f3bdfd2022b8845ad8f792aa5825) >> 128;
if (absTick & 0x2000 != 0) ratio = (ratio * 0xa9f746462d870fdf8a65dc1f90e061e5) >> 128;
if (absTick & 0x4000 != 0) ratio = (ratio * 0x70d869a156d2a1b890bb3df62baf32f7) >> 128;
if (absTick & 0x8000 != 0) ratio = (ratio * 0x31be135f97d08fd981231505542fcfa6) >> 128;
if (absTick & 0x10000 != 0) ratio = (ratio * 0x9aa508b5b7a84e1c677de54f3e99bc9) >> 128;
if (absTick & 0x20000 != 0) ratio = (ratio * 0x5d6af8dedb81196699c329225ee604) >> 128;
if (absTick & 0x40000 != 0) ratio = (ratio * 0x2216e584f5fa1ea926041bedfe98) >> 128;
if (absTick & 0x80000 != 0) ratio = (ratio * 0x48a170391f7dc42444e8fa2) >> 128;

ratio 是 Q128.128，但 sqrtPriceX96 是 Q64.96

为了最大限度地提高精度，getSqrtRatioAtTick() 在内部使用 Q128.128 numbers 执行平方和乘法算法，但以 Q64.96 的形式返回答案。价格的内部表示是 ratio 变量。

平方和乘法预计算回顾

为了解释 Uniswap V3 如何推导出上面显示的大常量，我们必须首先回顾平方和乘法算法。

平方和乘法算法依赖于预计算底数的幂。我们现在表明，代码中的大常量是从重复平方 1.0001−1/2 派生的。

使用平方和乘法算法，getSqrtRatioAtTick() 预计算

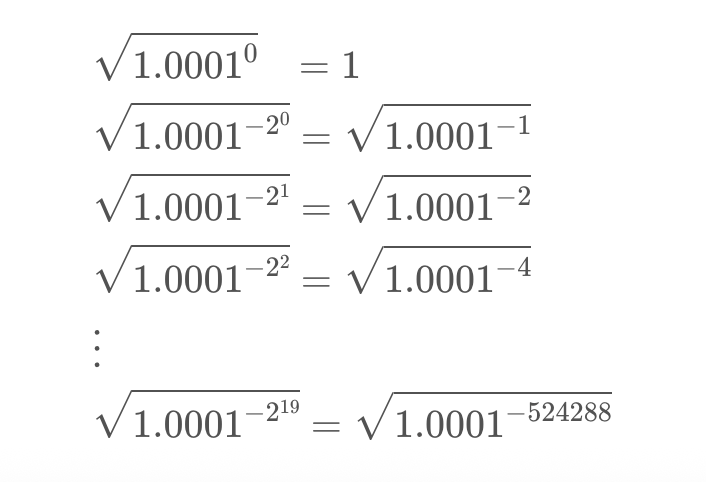
Uniswap V3 中的最小和最大 ticks 分别为 -887,272 和 887,272。但是，由于 getSqrtPriceRatioAtTick 仅直接计算负数部分，并通过倒数计算正数 ticks，因此它只需要计算 ticks [-887,272,0]。编码高达 887,273 的数字（887,272 加 0）所需的位数是 20，因为 ⌈log2⁡887,272⌉=20。这就是预计算值范围从 1.00010, 1.0001−20,…, 1.0001−219 的原因。

例如，假设我们要计算 tick -100 的价格。我们可以将 tick -64、-32 和 -4 的预计算值相乘，如下所示：

将大常量值推导为 Q128.128 numbers

我们现在展示 Uniswap V3 如何推导出大常量。

Tick 0 的平方根价格

大常量 0x100000000000000000000000000000000（紫色框）是 Q128.128 定点数 1（相当于 2 << 128）。

这对应于 tick 0，$ \sqrt {1.0001^0} = 1 $。考虑到如果 tick = 0，那么 absTick & 0x1 != 0 在第 27 行（橙色框）将为假，从而触发三元运算符的第二部分。

如果此 tick 为 0，则没有其他位为 1，因此随后的条件 if (absTick & 0xXX !=0) 都不为真，这意味着 ratio 将等于 0x100000000000000000000000000000000，而无需进一步修改。 这是预期之中的，因为将一个数字的零次幂返回 1。

Tick -1 的平方根价格

如果我们在 Python 中以 Q128.128 计算 tick -1 的价格，我们会得到以下结果：

>>>
0xfffcb933bd6f b0000000000000000000 # 为了清晰起见，添加了间隙

当转换为十六进制时，它接近下面高亮显示的幻数，但很明显，我们上面的估计值末尾有更多的零，这意味着它有精度损失：

这是 Uniswap 的 1.0001−1 常数与我们的估计值相比：

## Uniswap 的常量
>>> hex(0xfffcb933bd6fad37aa2d162d1a594001)
0xfffcb933bd6f ad37aa2d162d1a594001 # 为了清晰起见，添加了间隙

## 我们的常量
>>> hex(int(2**128 * math.sqrt(1.0001**-1)))
0xfffcb933bd6f b0000000000000000000 # 为了清晰起见，添加了间隙

## 请注意，Uniswap 的估计值和我们的估计值在间隙后有所不同

在下一节中，我们将展示如何改进我们的估计以匹配 Uniswap V3 的估计。

通过使用 Decimal 和重新排列除法来改进我们的常量计算

默认情况下，Python 浮点数没有足够的精度来计算具有 128 位精度的数字，但我们通过使用 Decimal 库来解决这个问题，该库为我们提供了我们想要的尽可能多的精度：

from decimal import *
getcontext().prec = 100 # 使用 100 位小数的精度约为 333 位

此外，为了消除涉及小数的不精确性，我们可以计算

作为

这消除了分数 1.0001。

我们可以通过避免负指数（具有隐含的除法）来再次提高精度。观察到我们可以通过翻转分子和分母来消除负指数：

$$ \frac { 1000 \bold1^{−1/2}} {10000^{−1/2}} = \frac { 10000^{1/2}} {1000 \bold1^{1/2} }$$

展望 tick -2，而不是为第二个负数 tick 计算 Decimal(10001)**Decimal(-2/2)（或 $ \sqrt {1.0001^{−2）} } $，我们直接将其简化为 Decimal(10001)**Decimal(-1)，以最大限度地减少在不需要它们的地方引入除法运算。

通过这种改变，我们现在可以更准确地重现 Uniswap V3 预计算的值。以下值乘以 2**128 以将它们转换为定点数：

from decimal import *
getcontext().prec = 100

## tick -1
print(hex(int(Decimal(10000)**Decimal(1/2) * 2**128 / Decimal(10001)**Decimal(1/2))))
## estim: 0xfffcb933bd6fad37aa2d162d1a594001
## uniV3: 0xfffcb933bd6fad37aa2d162d1a594001

## tick -2
print(hex(int(Decimal(10000)**Decimal(1) * 2**128 / Decimal(10001)**Decimal(1))))
## estim: 0xfff97272373d413259a46990580e2139
## uniV3: 0xfff97272373d413259a46990580e213a

## tick -4
print(hex(int(Decimal(10000)**Decimal(2) * 2**128 / Decimal(10001)**Decimal(2))))
## estim: 0xfff2e50f5f656932ef12357cf3c7fdcb
## uniV3: 0xfff2e50f5f656932ef12357cf3c7fdcc

## tick -8
print(hex(int(Decimal(10000)**Decimal(4) * 2**128 / Decimal(10001)**Decimal(4))))
## estim: 0xffe5caca7e10e4e61c3624eaa0941ccf
## uniV3: 0xffe5caca7e10e4e61c3624eaa0941cd0

## tick -16
print(hex(int(Decimal(10000)**Decimal(8) * 2**128 / Decimal(10001)**Decimal(8))))
## estim: 0xffcb9843d60f6159c9db58835c926643
## univ3: 0xffcb9843d60f6159c9db58835c926644

请注意，我们对代码中常量的计算仅比实际代码值少 1，这意味着 Uniswap V3 正在向上舍入十进制数以获得其常量。

总而言之，getSqrtRatioAtTick() 中的每个“幻数”都是以下数字，表示为向上舍入的 128 位定点 number（tick 1 除外）。

第 4/5 部分：使用 Q128.128 numbers 计算倒数

如果原始 tick 为正数，则下面显示的代码行计算倒数。

我们现在解释为什么代码在分子中使用 type(uint256).max。请注意，ratio 是 Q128.128 number 的价格。

当将定点数 x 除以另一个定点数 y 时，我们需要将分子乘以比例因子 S，以防止比例因子取消。

x⋅Sy

Q128.128 中“1”的值为 1 << 128 或 2128。要使用 Q128.128 计算 1 / ratio，我们执行以下操作：

2128ratio

我们需要将分子乘以比例因子，即 2128。这给了我们：

2128×2128ratio=2256ratio

但是，值 2256 无法在 Solidity 中编码，可以编码的最大值是 2256−1 或 type(uint256).max。

这意味着为正数 ticks 计算的价格将略有向下舍入。本文末尾讨论了这一点的含义。

第 5/5 部分：将 ratio 转换为 sqrtPriceX96 并向上舍入

最后一行代码转换 ratio，这是一个 Q128.128 number 到一个 Q64.96 number，同时向上舍入并返回该值。

sqrtPriceX96 = uint160((ratio >> 32) + (ratio % (1 << 32) == 0 ? 0 : 1));

本文未涵盖的重要细节

我们对本文中的代码进行了以下观察：

• 除了 tick -1 之外，常量都向上舍入
• 计算正数 ticks 的倒数会稍微向下舍入，因为代码将 2256 近似为 type(uint256).max。
• 如果将 ratio 除以 1 << 32 不完全（请注意上面的代码片段中的三元运算符，如果 ratio 不能完全除 1 << 32，则加 1），则从 Q128.128 到 Q64.96 的最终转换会向上舍入。

准确性的经验测试

只需将代码复制到 IDE 中即可轻松完成对 Solidity 函数的测试。

我们可以用 Python 创建一个参考实现，如下所示，以获得正确的

2961.0001i

作为价值

from decimal import *
getcontext().prec = 1000 # 将精度设置得很高
## 2**96 * (1.0001)^(tick/2)
math.ceil(Decimal(2**96)*(Decimal(10001)/Decimal(10000))**(Decimal(tick)/2))

（注意：也可以使用在线全精度计算器）。

我们可以比较极端 ticks 的输出：

## tick 887272 (MAX_TICK)
solidity: 1461446703485210103287273052203988822378723970342
python  : 1461446703485210103244672773810124308346321380903

## tick 0
solidity: 79228162514264337593543950336
python  : 79228162514264337593543950336

## tick -887272 (MIN_TICK)
solidity: 4295128739
python  : 4295128739

如果我们检查 MAX_TICK，我们会发现 Solidity 代码高估了真实值：

solidity: 14614467034852101032 87273052203988822378723970342
python  : 14614467034852101032 44672773810124308346321380903

此错误是否严重取决于下游逻辑如何使用此函数。

当流动性提供者添加或删除流动性以及交易者进行跨越 tick 的交换时，会使用 getSqrtRatioAtTick()。由于我们在 Uniswap V3 教程的这个阶段尚未讨论这些机制，因此我们推迟对该函数的错误分析。

总结

为了计算某个 tick 处的平方根价格，getSqrtRatioAtTick() 首先计算 tick (i) 的绝对值，然后循环遍历 i 的 20 个最高有效位以计算 1.0001−i/2。如果原始 tick 为正数，它会将价格重新计算为 1/1.0001−i/2。最后，它将 128 位定点表示形式转换为 96 位表示形式，然后将其作为价格返回。

• 原文链接： rareskills.io/post/unisw...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～