本要被破解但未发生的方法：Koblitz 和 Miller

本来要被破解，但就是没发生：Koblitz 和 Miller

当我与 Christof Paar 交谈时，有一句话让我印象深刻：“许多人认为，一旦研究人员认真研究椭圆曲线方法，最终会被破解”，但是，自 1987 年以来，它们通过 ECDH、ECDSA、EdDSA 和许多其他出色的密码学方法为我们提供了良好的服务。向 Kolitz 和 Miller 致敬。虽然他们花了一段时间才被采纳，但它现在是我们在线安全的核心。但是，可悲的是，量子计算机可能会终结椭圆曲线密码学，但我们应该感谢它至少二十年来提供的出色安全性。

简介

你的在线安全从根本上取决于一条漂亮的小曲线：椭圆曲线。 面对 RSA 不断增加的密钥长度，以及离散对数（如 Diffie-Hellman 密钥交换方法中使用）的弱点，它是网络安全的救星。 对于 RSA，我们正在转向 2,048 位的密钥长度，但对于椭圆曲线方法，我们的私钥长度通常只有 256 位长。 例如，如果你拥有比特币，那么让你拥有加密货币的私钥只有 256 位长。

谁发现了它？ 嗯，Neal I. Koblitz 和 Victor Miller 在 20 世纪 80 年代独立发现了该方法，并且该方法花了大约 20 年的时间才真正被采用。 2021 年，他们在真实世界密码学会议上因其工作而获得 Levchin 奖：

他们俩都应该获得该奖项，因为他们彼此独立地发现了 ECC[1]，这里：

和 [2] 这里：

他们的想法来自 Lenstra 在使用椭圆曲线破解 RSA 方法方面进行的初步工作：

虽然他们在 1985 年至 1987 年间提出了想法，但 ECC 的主要方法直到 2005 年才开始流行。 该方法的一大优点是我们扩展了现有方法（例如 Diffie-Hellman 方法）到 ECDH（椭圆曲线 Diffie-Hellman）的方式，并且几乎是直接替代品。 对于数字签名，ECDSA（椭圆曲线数字签名算法）方法现已被采用为许多应用程序的标准，包括比特币交易。 总体而言，糟糕的实施导致了一些问题，例如通过侧信道分析发现私钥的问题，但这些问题已根据 Peter Montgomery 在微软公司关于乘法过程的工作而得到克服：

Neal I. Koblitz

Neal I. Koblitz 是华盛顿大学的数学教授。 他是椭圆曲线密码学 (ECC) 的共同发明人。 他的原始论文发表于 1987 年，题为“椭圆曲线密码系统”[1]：

总的来说，ECC 是密码学领域最伟大的突破之一，它在很大程度上取代了密钥交换中的离散对数方法，并在许多数字签名应用中取代了 RSA 方法。 事实上，ECDSA 是比特币和以太坊使用的标准签名。

Neal 最近因其在真实世界密码学会议上的工作而获得了 Levchin 奖。 他最近的工作包括格子密码学和随机预言的应用。 Neal 也是几本领先教科书的作者：

• Koblitz, N. (1994). A course in number theory and cryptography (Vol. 114). Springer Science & Business Media.
• Koblitz, N. I. (2012). Introduction to elliptic curves and modular forms (Vol. 97). Springer Science & Business Media.

这就是 Neal：

Victor S Miller

Victor 是 Nexus 实验室的高级研究科学家。 他于 1975 年在哈佛大学获得数学博士学位，并于 1973 年至 1978 年在马萨诸塞大学波士顿分校担任助理教授。此后，Victor 先后在 IBM 研究中心、普林斯顿国防分析研究所、Meta Platforms 和 SRI International 工作。

在他的研究中，Victor 专注于计算数论、数据压缩和密码学领域。 他与 Neal Koblitz 一起是椭圆曲线密码学的共同创建者、Miller 算法的发明者，也是 LZW 数据压缩方法的共同发明者。 由于 LZW 的发明，他获得了 IEEE 千年奖章，由于他在椭圆曲线密码学方面的工作，他获得了 RSA 数学卓越奖、Levchin 奖和 Eduard Rhein 基金会技术奖，并且还是信息系统安全协会名人堂的成员。

椭圆曲线密码学

那么，在互联网上，什么比其他任何东西更能保护你的隐私和安全？ 那就是椭圆曲线，尤其是：

y ² = x ³+a x +b

其中 4a³+27b² ≠ 0（这是避免奇点所必需的）。 最流行的曲线是 Secp256k1（或 Curve 25519），定义为 a=0 和 b=7：

y² = x³+7 [链接]

在此中，通过 ECC（椭圆曲线密码学），我们取一个随机数 (n) 和椭圆曲线上的一个点 (G)，然后将它们相乘得到 P：

P = n G

G 将是 Bob 和 Alice 都会同意的曲线上的一个 (x,y) 点。 n 将是 Bob 的私钥，P 将是他的公钥。 挑战在于，如果 n 是一个 256 位的随机值，即使我们知道 G 和 P，也很难找到该值。

那么让我们看一段 Python 代码来设置椭圆曲线：

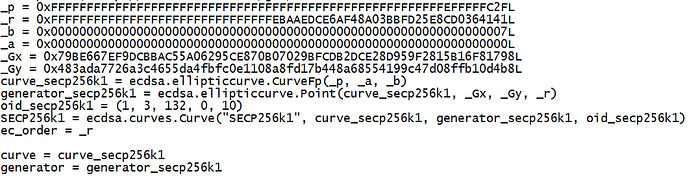
在这种情况下，我们看到 _a 为 0，_b 为 7 (y² = x³+7)，并且我们有一个 _Gx 和一个 _Gy 值。 我们还有 _p，它是一个素数，其中所有运算都使用 (mod _p) 函数执行。 在 Python 中，我们可以使用以下代码创建两个密钥对（一个用于 Alice，一个用于 Bob）：

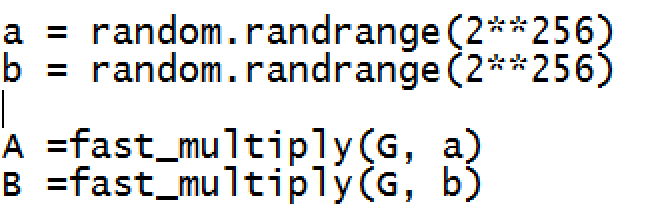
我们为 a 生成一个随机的 256 位值，然后通过将其与 G 相乘来找到公钥 (A)。这将为我们提供椭圆曲线上的一个点。 请注意，所有运算都是使用 (mod _p) 进行的，其中 mod 运算符是整数除法的余数。

分析密钥

当我们使用 OpenSSL 生成密钥对时，我们会看到一个 256 位的私钥（由 32 个字节组成）以及一个 65 字节的公钥。 公钥开头的 04 是一个标识符。 有两个 256 位的点定义了公钥（每个点长 32 个字节）：

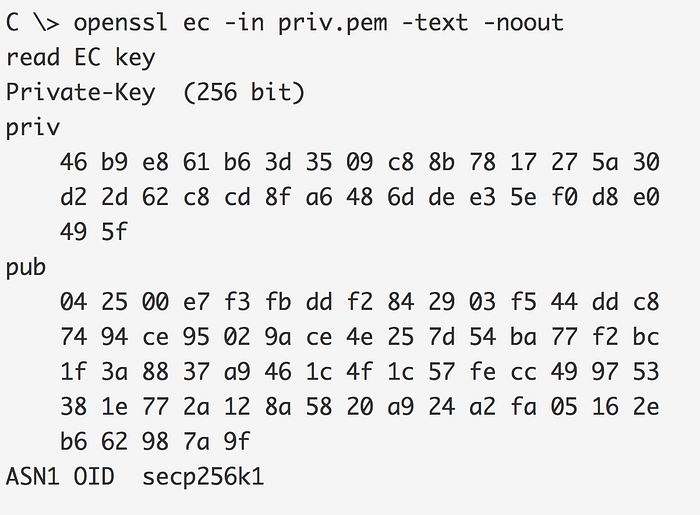
在这种情况下，私钥是：

公钥是：

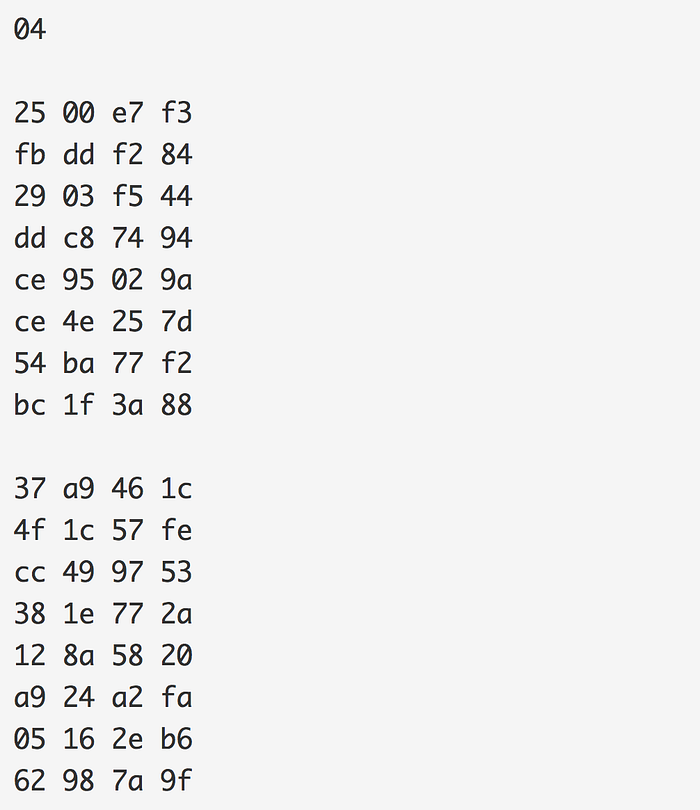
可以使用以下命令查看共享的椭圆曲线参数：

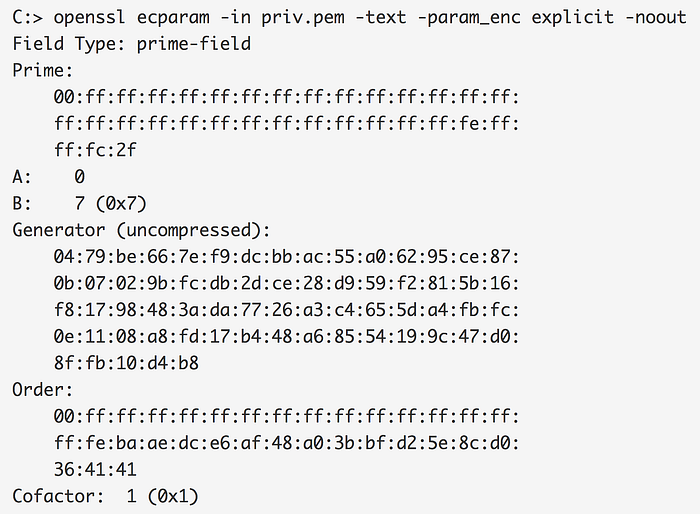
请注意，此处的 Prime、A、B 和 Generator 的值与上面 Python 代码段中的 _p、_a、_b、_Gx 和 _Gx 的值相同，并且对于此曲线标准的任何应用，这些值都可能相同。 如果你有兴趣，可以在此处定义一些曲线参数标准。

ECC 应用 - 数字签名和密钥交换

ECC 的两个主要应用是数字签名和密钥交换。 在密钥交换中，我们可以采用与常见的 Diffie-Hellman 方法类似的方法：ECDH。 通过这种方式，Bob 和 Alice 都生成他们的密钥对，然后交换他们的公钥值。 接下来，将这些值乘以他们自己的私钥，他们最终应该得到相同的点。 该点的 x 值通常用作共享值，它可以用于生成加密密钥 [链接] [真实示例]：

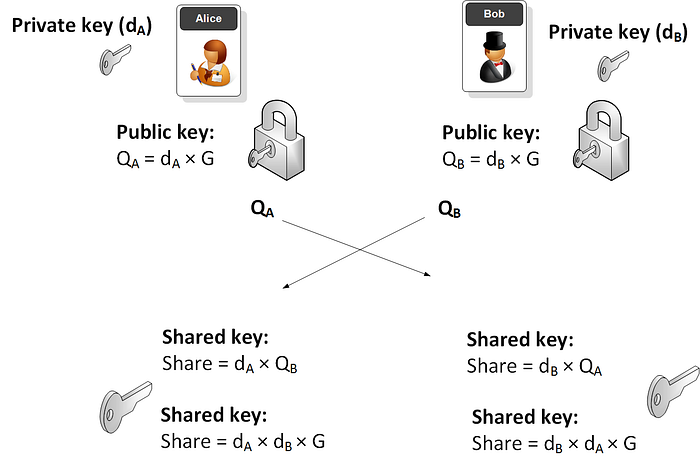
一个简单的例子是 [链接]：

Basepoint: (920 (mod 3851), 303 (mod 3851))
Alice's secret key: 25720
Bob's secret key: 15297
==========================
Alice's public key: (1996 (mod 3851), 3624 (mod 3851))
Bob's public key: (94 (mod 3851), 884 (mod 3851))
==========================
Alice's shared key: (2636 (mod 3851), 3251 (mod 3851))
Bob's shared key: (2636 (mod 3851), 3251 (mod 3851))
==========================
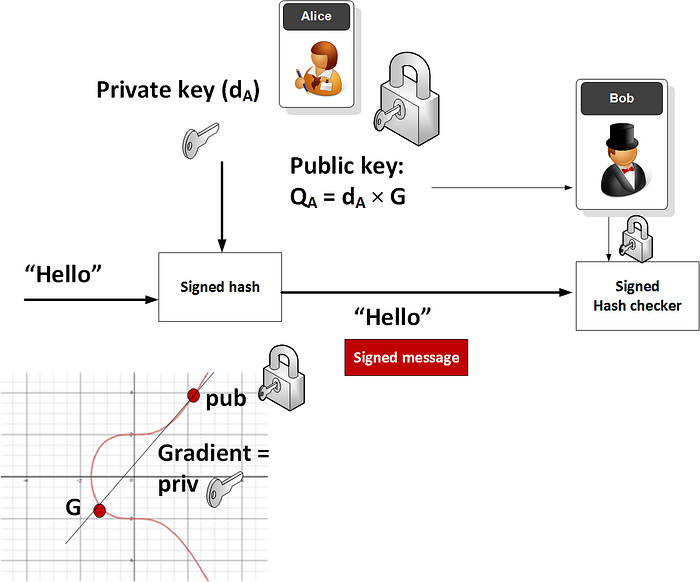
The shared value is the x-value: 2636

ECC 的另一个应用是签名，例如椭圆曲线数字签名算法 [这里]。 通过这种方式，Alice 将生成一个密钥对，然后使用她的私钥加密消息的哈希值。 然后，她将消息和签名后的哈希值发送给 Bob，Bob 获取他自己的消息哈希值，并使用 Alice 的公钥解密 Alice 的哈希版本。 如果哈希值匹配，则他已证明该消息是 Alice 发送的，并且该消息未更改：

在你的收件箱中获取 Prof Bill Buchanan OBE FRSE 的故事

免费加入 Medium，以获取来自这位作者的更新。

缩放图像将显示

比特币地址和签名

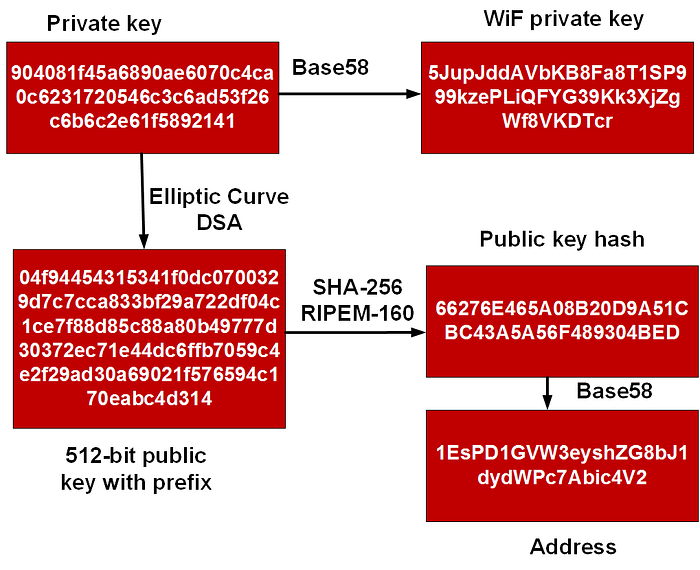
椭圆曲线在互联网、智能卡和物联网应用中随处可见。 你还可以在区块链中看到它，它被用作签署交易的标准方法。 通过这种方式，Bob 有一个钱包，其中包含他的公钥和私钥。 私钥用于签署他的交易，公钥将证明是他签署的交易。 我们还从密钥对生成 Bob 的 ID。

通过这种方式，Bob 最初创建一个 256 位的值，这将是他的私钥。 该密钥被转换为 Base-58 格式（它可以消除难以辨认的字符，例如“O”和“l”[此处]）。 这是他的 WiF（钱包交换格式）私钥。 他不应该向任何人透露这一点，并且如果可能的话，不应该在线存储它。 接下来，他将生成他的 512 位公钥（如上所示）。 之后，使用 SHA-256 和 RIPEM-160 对其进行哈希处理，以生成公钥哈希值。 然后使用 Base-58 将其转换为 Bob 的比特币 ID：

这方面的一个例子是：

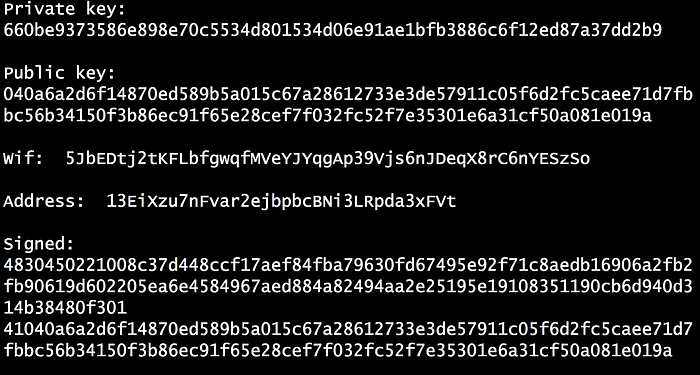
因此，如果我们要向 Bob 发送比特币，我们所需要做的就是获取他的地址，然后使用我们的公钥签署交易。

添加点

我们知道如何将椭圆曲线上的点乘以标量值（我们的私钥），但是我们可以添加我们的点吗？ 如果我们取两个点为：

P1 = n.G

P2 = m.G

如果我们添加这些点，我们会得到：

P1 + P2 = n G + m G = (n + m) G

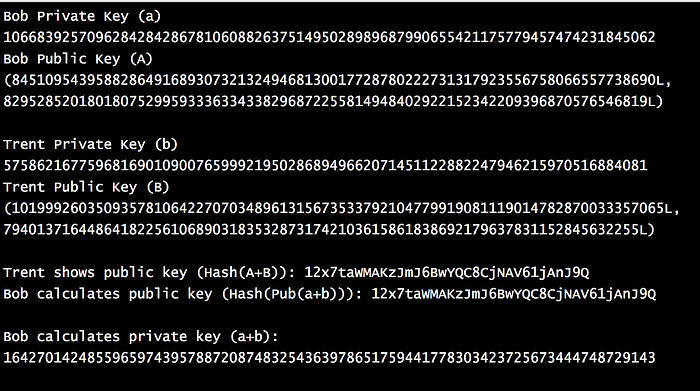
因此，如果我们添加公钥 (P1 + P2 (mod p))，则等效的私钥将是 (n + m (mod p))。 如果 Bob 有一个私钥 (a) 和一个公钥 (A)，然后 Trent 有一个私钥 (b) 和一个公钥 (B)。 那么公钥将是 A+B，私钥将是 a+b。 以下是一个示例 [这里]：

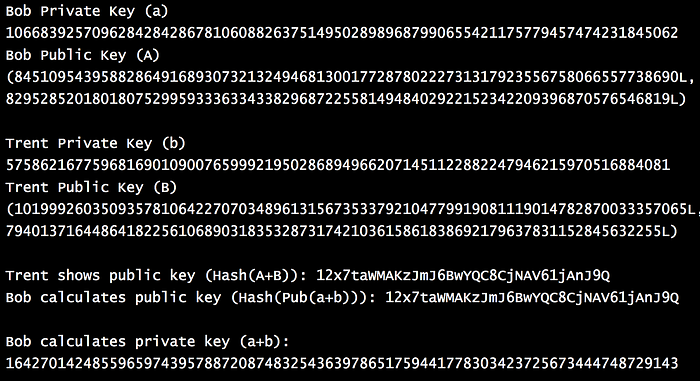
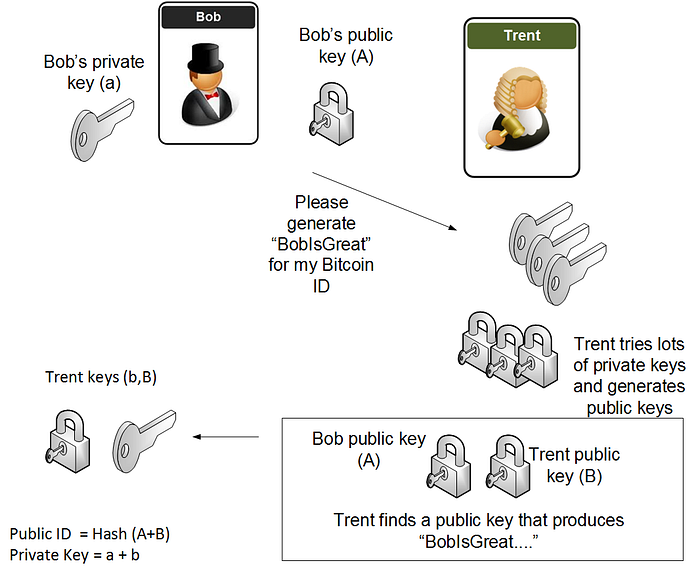
这方面的一个应用是 Trent 生成一个密钥，Bob 可以使用该密钥为生成的公钥生成一个等效密钥：

缩放图像将显示

使用 fast_add() 和 fast_multiply() - 取自 Bitcoin 库 - 我们可以这样实现：

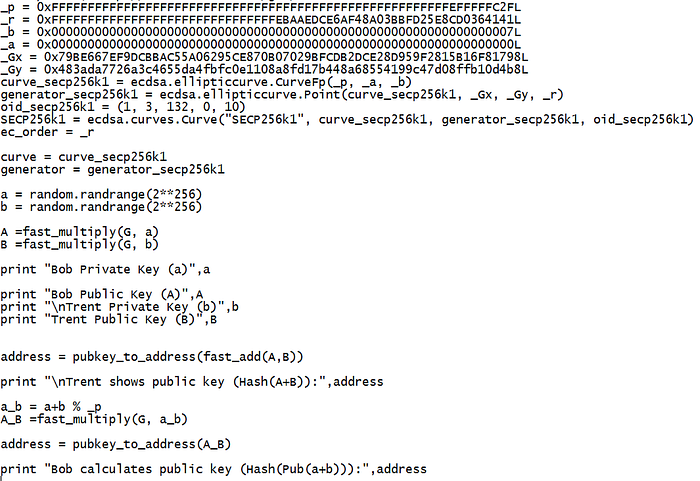
一个示例运行是：

通过 BN 曲线进行密钥配对

椭圆曲线在公钥加密中被广泛使用（例如在比特币和 Tor 中）。 BN 曲线（Barreto-Naehrig 曲线）[论文] 定义了一种椭圆曲线，可用于配对，从而实现高安全性和效率水平。 此页面使用 256 位 BN 曲线上的配对，并推导出消息的签名。 椭圆曲线密钥配对也与 zk-SNARK 和零知识证明一起使用。 它可以用于“加密乘法”。

对于椭圆曲线密码学，我们为私钥 (p) 生成一个 256 位的随机数，然后取椭圆曲线上的一个点 (G) [x,y]，然后将其乘以私钥以获得另一个点 (p×x,p×y)。 通过这种方式，我们得到 P=p×G，其中 G 是椭圆曲线上已知的点，P 是我们的公钥，p 是我们的私钥。

通过配对，我们可以推导出点之间更复杂的关系，例如，如果 P=G×p、Q=G×q 和 R=G×r，我们可以检查是否 r=p×q，但我们只知道 P、Q 和 R（公共值）。 目前，即使我们知道 P 和 G，我们也不能从 P=p×G 计算 pp。 值的暴露是有限的，因为我们可以计算 R=G×p×q，并且无法确定 p 或 q。

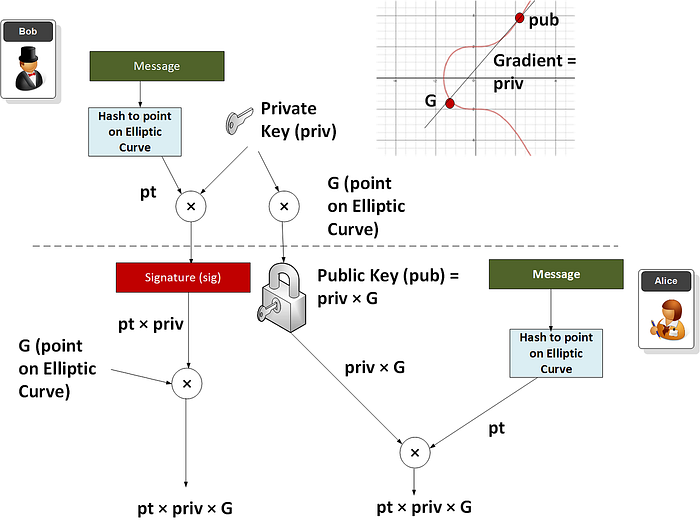
以下代码集成了 BN-256 代码。 让我们通过简单地为消息创建签名来测试代码。 Bob 将获取一条消息并使用他的私钥创建签名，Alice 将使用他的公钥来验证它。

首先，我们获取消息并将其哈希处理为椭圆曲线上的一个点 (pt)。 接下来，我们获取私钥 (priv)（一个随机的 256 位值），然后将该点乘以 priv×pt。 这就是签名。 然后，Bob 通过将他的私钥 (priv) 乘以 G 来生成他的公钥，从而得到 priv×G。 然后，Alice 将获取消息并将其哈希处理为椭圆曲线上的一个点 (pt)。 接下来，她将其乘以 Bob 的公钥以获得 pub×pt。 她还获取签名 (sig) 并将其乘以 G 以获得 sig×G。 如果签名正确，则生成的两个值应匹配 [这里]：

缩放图像将显示

结论

ECC 太神奇了！ 在这里尝试一些：

https://asecuritysite.com/ecc

参考文献

[1] Koblitz, N. (1987). Elliptic curve cryptosystems. Mathematics of computation, 48(177), 203–209.

[2] Miller, V. S. (1985, August). Use of elliptic curves in cryptography. In Conference on the theory and application of cryptographic techniques (pp. 417–426). Springer, Berlin, Heidelberg.

• 原文链接： medium.com/asecuritysite...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～