隐私货币:第三部分
- bhargav
- 发布于 2025-08-22 22:06
- 阅读 2111
本文深入探讨了Zcash中用于防止双重支付并保护隐私的机制,重点介绍了Zcash如何通过zk-SNARKs和nullifier集来验证交易,同时探讨了Merkle树在处理Zcash交易中的局限性,并提出了使用集合非包含累加器(set non-inclusion accumulator)的解决方案,以实现更高效、可扩展的隐私保护。
背景
双重支付(Double-spending)是指某人试图多次使用相同的资金。这是金融领域的一个根本性问题,以各种形式出现。在传统银行业务中,这看起来像空头支票(check kiting)——操纵账户之间的浮动时间来弥补透支。一个臭名昭著的例子是Najeeb Khan的1.8亿美元欺诈案,他利用银行的时间窗口,以牺牲客户的利益为代价,资助奢华的生活方式。
在加密货币中,以太坊经典在2020年遭受了多次51%攻击,攻击者重写了交易历史,并双重支付了超过900万美元。这表明,没有安全共识的公共区块链也可能容易受到攻击。
Zcash提出了一个更复杂的挑战:它的屏蔽交易没有揭示关于发送者、接收者或价值的任何信息。为了在保护隐私的同时防止双重支付,Zcash强制执行两个加密约束:
- 隐私包含证明(Private inclusion proof):note1 必须在 note-commitment Merkle 树中。
- 公开的非包含证明(Public non-inclusion proof):note的 nullifier 必须不在 nullifier 集合中。
为什么 Zcash 使用公开的非包含检查(public non-inclusion check)
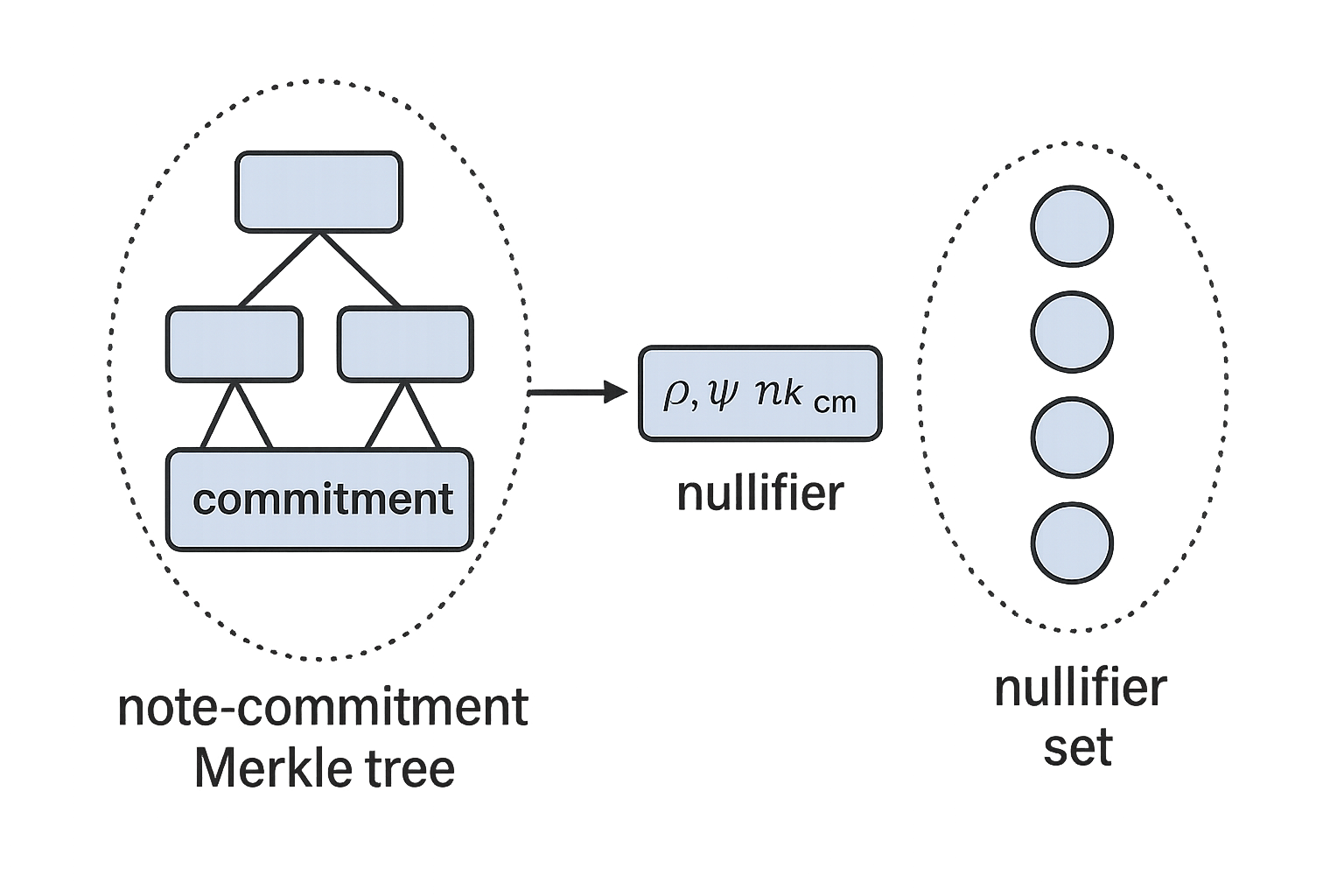
当创建一个新的屏蔽 note 时,只公开它的 commitment。这被附加到全局 note-commitment Merkle 树上,而 note 的实际价值和接收者保持隐私。因为树是只追加的,并且不跟踪花费,所以第二个标签——nullifier——确保每个 note 最多被花费一次。
Nullifier 是 note 的一个确定性的、不可链接的指纹。它使用由 note 的密钥控制的伪随机函数(pseudorandom function) (PRF)计算。只有所有者可以导出 nullifier,并且每个 note 只有一个2。
“如果一个交易会将一个已经存在于集合中的 nullifier 添加到 nullifier 集合中,那么这个交易就是无效的。”
nullifier 被公开并对照 nullifier 集合进行检查,nullifier 集合与 Merkle 树一起在每个区块中更新。这允许网络拒绝双重支付,同时对 note 本身一无所知。
隐私成员证明(Private membership proof)
Zcash 使用 zk-SNARKs 来强制执行 commitment 包含和 nullifier 一致性这两个约束,而无需透露花费的是哪个 note。每个证明大约 1-2 kB,可在几毫秒内验证,甚至适用于[轻客户端(light client)]3。
1. zk-SNARK 内部创建的隐私链接
Merkle 包含:
证明者提供 note commitment $cm$4 和 Merkle 认证路径 π\piπ 作为隐私 witness 数据。电路强制执行:
$$\text{MerkleRoot}(cm, \pi) = \rho_t $$
其中 $\rho_t$ 是 anchor,这是一个公共输入,表示区块高度 ttt 时的 Merkle 根5。这确认 $cm$ 出现在历史 note-commitment 树中的某个位置。
Nullifier 计算:
在同一个电路中,证明者使用以下公式重新计算 nullifier:
$nf = \text{PRF}_{nk}(\rho_t, \psi, cm)$
其中$(nk, \psi)$是从 note 中导出的密钥。输出 nullifier $nf$ 被公开,并绑定到相同的 anchor 和commitment。
这种内部链接确保了 SNARK 证明了所揭示的 nullifier 和它所导出的隐私 note 之间的一致性——而没有揭示关于 note 本身的任何信息。
2. 链上检查如何工作
每个交易都在证明的公共输入中包含 anchor $\rho_t$ 和 nullifier $nf$。一旦 SNARK 验证通过,每个全节点都会检查:
- nullifier $nf$ 尚未 存在于 nullifier 集合 $N(t)$ 中。
- 如果检查通过,则区块更新: $N(t+1) = N(t) \cup {nf}$
这确保了每个 nullifier 最多出现一次——强制执行一次性可花费性。
3. 为什么这两个链接就足够了
- 存在性(Existence):Merkle 等式证明了真实的 commitment $cm$ 已经存在于根为 $\rho_t$ 的树中。
- 唯一性(Uniqueness):PRF 将单个 nullifier $nf$ 绑定到该 $cm$,并且共识允许每个 $nf$ 仅出现一次。
因此,任何有效的交易都必须:
- 引用一些现有的 note(通过包含 $cm$),
- 并且不能重用该 note(因为它的 $nf$ 已经存在于 $N$ 中)。
包含证明和非包含检查通过共享变量 $(cm, \rho_t, nf)$ 在 SNARK 内部和链上进行数学固定。
Merkle 树的局限性
增量 Merkle 树6是 Zcash 记录屏蔽 note 的经典方法7。它们具有固定的深度 $d$,因此账本最多可以接受 $2^d$ 个 commitment,然后才需要迁移。每个新的 note 都会成为一个新的叶子,并且树的抗冲突哈希允许证明者稍后使用 $d$-hash 路径显示包含。该路径的大小是恒定的并且是高效的,但是树的状态永远增长8。
分片(Sharding)有所帮助,但不能解决问题
一个自然的下一步是分片(shard) Merkle 树。账本不是维护一个整体,而是维护许多子树(例如,$2^{32}$ 个叶子树)。当一个分片填满时,会打开一个新的分片,并且一个小的 根之根树(root-of-roots tree) 跟踪当前的分片根。现在,note 的包含路径包括:
- 一个短的 分片内(intra-shard) Merkle 路径
- 一个额外的哈希值到达根之根
这种设计保持了证明的大小,并且减少了钱包更新的开销:客户端只需要跟踪包含其 note 的分片中的更改9。
但即使这样也是一个临时性的修复。根之根本身也是增量的,并且最终会被填满。只要分片处于活动状态,就必须更新历史路径。状态修剪仍然很困难,因为每个铸造的 note 都必须保持可访问。因此,账本大小和钱包同步带宽随着协议的生命周期线性增长。
为什么集合非包含累加器(set non-inclusion accumulator)会改变一切
集合非包含累加器(set non-inclusion accumulator) 提供了一种更简单的方法来跟踪已花费的 note。
虽然增量 Merkle 树非常适合包含证明,但它们不能有效地支持非包含证明。累加器通过将所有 note 折叠成一个固定大小的累加器值 $A_t$ 来解决这个问题,该累加器可以处理非包含证明(并且可以轻松扩展以支持包含证明)。每次插入都是一个简洁的多项式 commitment 更新,并且可以丢弃旧的累加器状态——因为 IVC(增量可验证计算)链证明了更新的正确性。
关键的优势是简单性:虽然 Merkle 树需要单独处理 commitment 和 nullifier,但累加器提供了一个单一的加密原语,可以处理非包含证明。这意味着我们可以将相同的系统用于 nullifier 集合,并在需要时扩展它来处理 note commitment。
神奇之处在于累加器的递归结构:每次更新都会证明插入了一个 note 向量,而不包括特定的元素 $x$。非成员资格声明是逐步维护的,证明插入的每个多项式缺少 $x$ 作为根——这意味着 $x$ 不存在。这把问题变成了一个递归代数问题,而不是存储问题。
最后,证明非包含(“这个 nullifier 从未插入到 $A_t$ 之前”)只需要检查一个多项式(折叠到累加器中的多项式)确实有 $x$ 作为根。
- 累加器的大小永远不会增长,无论插入多少个 note
- 没有深度上限或耗尽的叶子索引
- 每个 IVC 步骤只是几个哈希和群操作——即使在链上也很有效
- 你不需要跟踪最后 $k$ 个 epoch 之前的历史状态——只要生成了跨越该范围的所有证明,就可以安全地丢弃较早的累加器数据
简而言之:屏蔽的匿名性可以无限增长,无需迁移或树维护。这是 Project Tachyon 的累加器设计的基础——一个更简单的系统,可以有效地处理非包含证明。
实现
累加器从一个微不足道的状态 $A_0 = \langle(1,0,0,\ldots), G\rangle$ 开始,并且每次我们插入一个域元素向量 $ ai = (a{i,1},\dots,a_{i,k}) \subset \mathbb F$ 时都会更新。经过多次更新后,我们想要证明,对于选定范围 $[j,\,m)$ 中的 每个 步骤,插入的向量从未包含某个元素 $v$。我们不存储所有过去的向量,而是将它们折叠成一个单个曲线点累加器,其大小永远不会增长。
神奇之处在于,虽然我们在内部跟踪越来越多的 nullifier——每次构建一个更大的多项式——但我们只在链上存储一个单点。这个点充当我们所见过的所有 nullifier 的加密摘要,就像 Merkle 根一样,但没有树。这意味着区块链状态保持很小,即使我们处理数百万笔交易。
1. 插入:折叠一个根的向量
对于当前步骤,我们首先构建它的 vanishing polynomial
$ai(X)=\prod{r\in\mathbf a_i}(X-r),$
然后对系数向量做一个 Pedersen commitment $P_i$。一个 Fiat–Shamir 挑战 $h=H(A_i,P_i)$让我们跳到下一个状态
$$ A_{i+1} = [h] A_i + P_i .$$
pub fn insert(roots: &[Fr], a_prev: G1Affine, r: Fr) -> Result<State> {
let poly = poly_from_roots(roots); // a_i(X)
let p_i = commit(&poly.coeffs, r)?; // P_i
let h = hash_points_to_fr(&a_prev, &p_i); // H(A_i,P_i)
let next = a_prev * h + p_i; // A_{i+1}
Ok(State { Accumulator: next.into_affine(), Commitment: p_i })
}关键点: 无论我们添加多少向量,Accumulator 始终是一个 单点。
2. 证明一个新鲜值 $v$ 不在今天的根中
验证者只有在我们 commitment 的多项式在 $v$ 处不消失时才会接受。
-
评估一次:$\alpha = a_i(v)$。如果 $\alpha=0$ ,则证明必须中止(v 是一个根)。
-
移动 commitment,以便移动后的多项式_确实_在 $v$ 处消失: $P'_i = P_i - [\alpha]G_0$
-
使用第二个挑战 $ h' = H(S_i, P'_i)$ 来跳过非成员资格累加器。
pub fn check_non_membership(
roots: &[Fr], v: Fr, r: Fr, s_prev: G1Affine) -> Result<State>
{
let poly = poly_from_roots(roots);
let alpha = evaluate_poly(&poly.coeffs, v); // α = a_i(v)
assert!(!alpha.is_zero()); // must be non-root
let p_i = commit(&poly.coeffs, r)?; // P_i
let p_ip = p_i - POINTS[0] * alpha; // P'_i
let h_p = hash_points_to_fr(&s_prev, &p_ip); // h′ = H(S_i,P′_i)
let next = s_prev * h_p + p_ip; // S_{i+1}
Ok(State { Accumulator: next.into_affine(), Commitment: p_i })
}因为 $a_i(v)\neq0$ ,所以_移动后_的 commitment 现在隐藏了一个多项式,该多项式在 $v$ 处唯一的根是我们人为创建的——这正是我们需要用于非成员资格的 witness。
3. 跨越带有 IVC 的范围的非成员资格
我们可以创建一个递归 (IVC) 证明,其中基本情况是$ (A_j,S_j)$ ,并对每个 i≥ji \ge ji≥j 重复上述步骤,以做出范围声明。
- 在电路中,我们从快照 $ (A_j,S_j)$ 开始。
- 在每次迭代中,我们见证 $ (P_i, \alpha_i) $ 并应用
check_non_membership跳跃。 - 累加器从 $ (A_i,Si) $移动到$ (A{i+1},S_{i+1})$ 。
- 只有当前状态跨越 IVC 边界;较早的数据将被丢弃。
经过 $m-j $跳跃后,验证者会看到$ (A_m,S_m)$ 。如果 S_m 在 $v$ 处展开为零,那么——通过归纳——每个中间多项式都被证明在 $v$ 处的值都非零。因此,$v$ 从未出现在任何根向量 $\mathbf a_j$ 中。
4. 这对 Zcash 风格的 nullifier 检查有何意义
- O(1) 状态:
Accumulator是一个点 $\rightarrow$ 没有 Merkle 深度上限。 - 忘记历史: 一旦存在 IVC 证明,我们就可以删除每个旧向量。
- 每个区块的成本都很低: 每次跳跃都是几个哈希和群操作
- 可扩展的非成员资格: 非常适合显示 nullifier _从未_出现,而无需在链上保留 nullifier 集合。
在实践中,用这个累加器替换 Zcash 的只追加 Merkle 树将消除锚泄漏和树维护,同时仍然证明 nullifier 是唯一的。
结论
向量承诺累加器为 Zcash 提供了一种更简单的方法来跟踪已花费的 note:固定大小的状态,可以有效地处理非包含证明(并且可以扩展以支持包含证明)。这消除了深度上限和树迁移,同时仍然提供与 Merkle 树相同的安全属性。
实际部署仍然存在开放性问题——元数据隐私、轻量级 witness 更新等。请查看我在下面实现的这个累加器。
| 原型(Prototype) | 想法(Idea) | 代码(Code) |
|---|---|---|
| 仅 PCS(PCS-only) | 累加器 + 多项式 commitment | https://github.com/0xWOLAND/set-noninclusion |
| 折叠证明(Folded proofs) | 相同的累加器,使用 zkVM SP1 逐块递归 | https://github.com/0xWOLAND/sp1-noninclusion 使用 SP1 构建 |
有关完整的设计草图,请参见 Sean Bowe 的 HackMD。
附录
向量承诺累加器保证了存在性(existence)(该值确实已插入)和唯一性(uniqueness)(没有两个不同的向量可以在同一索引处打开相同的 commitment),原因如下:
IVC 非成员资格链中的存在性
对于非包含,每个 IVC 步骤都声明 $p_t(z)\neq0$。因为多项式 $p_t$ _完全_编码了在步骤 ttt 处插入的向量,所以陈述“$z$ 不在 ${\bf v}_t$ 中”是正确的 当且仅当 评估是非零的。因此,最终的递归证明证明了对于范围内的每个步骤,$z$ 不是任何插入向量的坐标。这是关于整个历史的_存在性_陈述,仅以 $O(1)$ 验证者工作量实现。
类似 nullifier 的开放的唯一性
如果我们用一个导出类似 nullifier 的输出的向量承诺替换(例如,在 PRF 中包含索引 $j$ 和值 $v_j$),则唯一性遵循相同的逻辑:PRF 输出是_单个_有效开放的函数,并且 commitment 的绑定确保如果没有违反离散对数或抗冲突性,则没有第二个不同的开放可以产生相同的输出。
简而言之,承诺的代数绑定锚定存在性(anchors existence),而它们的线性独立性强制唯一性(enforces uniqueness)——这些属性可以在每次 IVC 更新中幸存下来,并使累加器具有与 Merkle nullifier 提供的相同的抗双重支付能力,但具有固定大小的状态和证明。
脚注
-
note $N$ 是值 $v$ 的加密表示,可以由相应屏蔽花费密钥的持有者花费 ↩
-
在 Orchard 中,nullifier 计算为 note 的两个随机数 ρ,ϕ\rho, \phiρ,ϕ、所有者的 nullifier 导出密钥 nknknk 和 commitment $cm$ 的 PRF。↩
-
轻客户端(Light client) 使用简洁的证明来验证状态转换,而不是下载整个链。这允许在低资源设备上安全运行。↩
-
因为 $cm$ 是一个 绑定 Sinsemilla commitment,如果没有 (i) 在哈希到曲线函数中找到冲突或 (ii) 解决离散对数问题(两者都假设为不可行),则两个不同的开放 (note,r)(\text{note},r)(note,r) 和 (note′,r′)(\text{note}',r')(note′,r′) 无法映射到相同的曲线点。如果你调整 note 的_任何_字段或选择一个新的 blinding 标量 r′r'r',你不可避免地会得到一个_不同_的点,因此得到一个不同的 $cm$。由于 zk-SNARK 内部的 Merkle 路径将花费绑定到已经位于树中的确切 $cm$,因此你无法“交换”替代的 commitment;你首先必须在单独的交易中铸造新的 $cm$。并且因为 nullifier 是一个明确包含 $cm$ 的 PRF,所以更改 commitment 也会更改 nullifier,因此链上双重支付检查仍然有效。↩
-
Zcash 中的每个区块都有一个高度为 note-commitment 树。创世区块的高度为 0,随后的每个区块将此高度递增 1。↩
-
增量 Merkle 树是一个二叉树,支持高效的只追加更新:每个新元素都作为下一个可用的叶子添加,并且只重新计算沿其路径到根的哈希值。这允许 Merkle 根随时间演变,而无需重建整个树,从而实现大小保持不变的短包含证明。↩
-
Zcash 使用增量 Merkle 树来维护所有屏蔽 note 的 commitment 树。创建每个 note 时,其 commitment 将附加到下一个空叶子。内部节点会动态更新,并且 Merkle 根会增量演变。包含证明很短(每个级别一个哈希),并且当前根用作每个交易中的公共 anchor。这实现了隐私保护花费证明,而无需透露花费哪个 note。 ↩
-
虽然树状态会增长,但可以有效地进行钱包 witness 更新:受信任的第三方可以仅提供 O(logn)O(\log n)O(logn) 建议,让客户端通过 $N$ 次插入来更新其 witness,而无需下载每个新叶子。这正是 Zashi 当前通过让服务器提供紧凑的更新提示来处理 witness 更新的方式,这些提示让钱包以最小的带宽保持同步。↩
-
分片(Sharding)解决了围绕 note 检测和可花费性的 UX 问题。 有关权衡和设计的详细信息,请参见此论坛帖子。↩
- 原文链接: bhargav.wtf/blog/zcash-p...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 后量子时代,我们如何保护隐私 214 浏览
- ZK编年史:哈希登场 170 浏览
- Layer Zero 发布 Zero 链:去中心化的多核世界计算机 373 浏览
- “Jolt Inside” - 构建者需要了解的全新武器 295 浏览
- 以太坊的下一个重大转变:从重新执行每笔交易到验证 ZK 证明 391 浏览
- Zcash:比特币遗忘的隐私 439 浏览
- ZK编年史:计算模型 310 浏览
- lambdaworks 2026 年更新路线图和优先级 377 浏览
- 2026年构建机构级DeFi平台真正需要什么 927 浏览
- zkMesh:2026年1月回顾 462 浏览
- 如果它能编译,那它就是正确的(几乎):Lean 4 在 ZK 系统和工程中的介绍 661 浏览
- Zcash 的时代到来了 797 浏览

