Glamsterdam 方程 - 权益证明
- 以太坊中文
- 发布于 2025-07-18 16:50
- 阅读 1119
本文提出了“Glamsterdam 方程”,旨在指导在较短的 slot 时间下,延迟执行 (delayed execution) 和 ePBS (enhanced Proposer Builder Separation) 之间的决策。
Glamsterdam 公式
非常感谢 @potuz 提供的模型反馈。 同时也感谢 @barnabe 和 @terence。
概述
Glamsterdam 公式旨在指导在 延迟执行 和 ePBS 之间做出决策,尤其是在 更短的 slot 时间 的背景下。 在一组基本假设下,计算得出两种 slot 流水线配置中的最大执行 gas/秒 和 blobs/秒。 然后,根据用户在扩展性、slot 时间、简洁性和去信任化之间的优先级,计算出一个效用最大化的 slot 配置。 Glamsterdam 公式应被视为一种工具。 它本身无法在辩论中给出明确的答案,原因有二:
- 有几个建模决策可能会使结果偏向任何一方。 为了生成易于概览的公式,进行了一些简化。 常数是通过_有根据的猜测_选择的,调整后会产生不同的结果。
- 我们对效用方程中更主观的常数有不同的看法。 主观品质,如去信任交换或简单设计的价值,未被量化,用户只需在 $U_O$ 中提供他们主观的量化。 他们还可以通过效用弹性来指定不同扩展组件的重要性。
整体 Glamsterdam 效用函数被指定为
$$U = (G^_s)^{U_G} \times (B^_s)^{U_B} \times (1/S^*)^{U_S} \times U_O,$$
依赖于在 gas/s, $G^_s$, 和 blobs/s, $B^_s$ 上的与Fusaka成比例的扩展,以及slot时间 S^*的相对减少。 指数是效用弹性(默认值为1),指定不同扩展组件的重要性。 这篇文章将首先分析推导出在各种slot时间下延迟执行和ePBS分别可以实现的扩展(遵循简化的假设),然后回到效用函数。然后改变常数,以分析在不同假设和优化下的结果。 最后,探讨了替代设计。
常数
slot 流水线方程最初在以下常数下进行分析,以假设的 Fusaka 基线作为起点:
| 符号 | 值 | 说明 |
|---|---|---|
| $L_G$ | 0.8 s | 全局延迟。 最小区块充分传播以形成共识所需的时间。 |
| $L_D$ | 0.8 s/MB | 数据延迟。 每个必须传播的MB数据所需的完整区块传播的额外时间。 |
| $L_{RF}$ | 0.2 s | 中继延迟。 将信标区块发送到中继的固定延迟。 |
| $L_{RD}$ | 0.15 s/MB | 中继数据延迟。 发送信标区块到中继站时,每 MB 数据所需的额外时间。 |
| $b_b$ | 1 MB | 信标区块大小。 必须容纳的信标区块的最大大小。 |
| $P_{bg}$ | 每 60M gas 1 MB | 每个 gas 的 Payload 字节数。 每个 gas 的 Payload 最大数据大小。 |
| $E_s$ | 60M gas/s | 执行速度。 每秒可以执行的最大 gas 量。 |
| $B_r$ | 15 blobs/s | Blob 速率。 每秒可以传播的最大 blob 数量(从 48 blobs/4-L_G s 导出)。 |
| $\bar{S} $ | 12 s | 基线 slot 长度。 基线 Fusaka slot 长度。 |
| $\bar{G}_s$ | 5M gas/s | 基线最大 gas 吞吐量。 在效用函数中用作参考点的基线最大 gas/s(60M gas/12 s)。 |
| $\bar{B}_s$ | 4 blobs/s | 基线 blob 吞吐量。 在效用函数中用作参考点的基线 blobs/s(48 blobs/12 s)。 |
| $A_a$ | 3 s | Attestation 聚合时间。 完整 attestation 聚合所需的时间。 |
| $\mathrm{PTC}_d$ | 1.4 s | Blob PTC 延迟。 在 slot 结束时传播 PTC 投票所需的余量。 |
| $A_d$ | 0.4 s | Builder 延迟。 在 ePBS 中,builder 在 attestation 截止日期后等待的时间,作为最坏情况,然后再发布 Payload。 |
总的中继延迟定义为 LR=L{RF} + b\text{b}L{RD},在整篇文章中使用 L_R 而不是写出单个组件。
常数是有根据的猜测,基于先前的分析和当前的发展,例如:1, 2, 3, 4, 5, 6, 7, 8, 9。 具有较高不确定性的常数的影响有时可能会平均化,从而产生实际的结果。 例如,数据延迟 LD 可能有些保守,而每个 gas 的 Payload 字节数 P{bg} 则更激进,假设对数据成本进行进一步调整。 为了帮助读者形成自己的观点:
- 用于运行分析和制作图表的源代码将在网上提供(本周末),
- 结论部分探讨了基线设置的变化。
分析的一个具体简化之处是,blob 和区块在 p2p 层的传播之间的交互未建模,而信标区块和 Payload 传播之间的交互已建模。 每个 slot 的 blob 数量仅从可用的传播时间(取决于 slot 结构)得出,并锚定在 Fusaka 规范上,包括与区块相同的全局延迟 L_G。 这使得分析更易于处理。 确切地知道 blob 如何与区块交互也是一个悬而未决的问题,考虑到各种验证者角色和 CL/EL 交互。
延迟执行
延迟执行使用简单的配置,没有特殊的头截止日期,并且 blob 必须在 attestation 时间可用。 分析的目标是设置 attestation 截止日期 A,以最大化效用,这是 gas 和 blob 吞吐量的函数。 可以包含在 slot 中的总 gas G 受执行和传播时间的限制。 Payload 传播的固定时间约束可以表示为
$c = L_R + LG + b\text{b}L_D,$
包括中继延迟和全局延迟,以及信标区块的传播(消耗固定量的带宽,该带宽不能同时用于 Payload)。 给定 gas 量 G 的最大 Payload 大小为 P{bg}G 字节,其中 P{bg} 是每单位 gas 的最大 Payload 大小。 传播此 Payload 的时间受可用窗口 A-c 的限制,这给出了约束:
$G \le \frac{A-c}{P_{bg} L_D}.$
Gas 也受到执行窗口 S-A 和执行速度 E_s (gas/s) 的限制,这给出了第二个约束:
$G \le E_s(S-A).$
可以最大化潜在 gas 吞吐量的截止日期 A_G 在 G 的两个限制相等时找到:
$E_s(S-A_G) = \frac{AG-c}{P{bg} L_D}.$
求解 A_G 得到:
$A_G = \frac{c + Es P{bg} L_D S}{1 + Es P{bg} L_D}.$
但是,总体目标是最大化效用,其中还包括 blob 吞吐量。 定义 slot 中的 blob 总数为 B。 效用函数的缩放项定义为 gas/s 和 blobs/s 相对于当前基线的变化(用横线高亮显示):
$G_s^ = \frac{G/S}{\bar{G}_s}, \;\;\;\;\;\; B_s^ = \frac{B/S}{\bar{B}_s}.$
通过最大化整体效用函数的缩放项的乘积来找到效用最大化的截止日期 A_U:
$U_2 = (G^_s)^{U_G} \times (B^_s)^{U_B}.$
一个有用的假设是,寻求的最优是受执行限制的(即,G \propto S-A),因为稍后的截止日期总是提高 blob 吞吐量。 为了找到这个最优值,分析了 log-utility \ln U_2。 忽略不影响相对于 A 的导数的常数项,该函数简化为:
$\ln U_2 = \text{const} + U_G \ln(S-A) + U_B \ln(A - L_G - L_R).$
相对于 A 求导得到:
$\frac{d}{dA}(\ln U_2) = -\frac{U_G}{S-A} + \frac{U_B}{A-L_G-L_R}.$
将导数设置为零并求解 A 得到最终表达式:
$A_U = \frac{U_B S + U_G (L_G+L_R)}{U_G + U_B}.$
然后,通过选择这两个候选者中较晚的一个来选择最终的最佳截止日期 A^*,该截止日期受允许 attestation 聚合的最晚截止日期 A_L = S - A_a 的限制:
$A^* = \min(\max(A_G, A_U), A_L).$
一旦选择了最终截止日期 A^*,就可以通过取两个限制的最小值来计算在该截止日期可以实现的总绝对 gas G:
$G = \min\left(Es(S-A^), \frac{A^-c}{P{bg} \cdot L_D}\right).$
由此,得出最终吞吐量。 每秒 gas 为:
$G_s = G/S,$
每秒 blob,由截止日期 A^* 和 blob 传播速率 B_r 确定,为:
$B_s = \frac{(A^*-L_G-L_R) \cdot B_r}{S}.$
图 1 显示了最佳 attestation 截止日期,它可以是:
- 在 Payload 传播时间和执行时间之间完美平衡(A_G;品红色),
- 在忽略 Payload 传播时间的约束时,在效用最优值处(A_U;红色),
- 在允许 attestation 聚合的最晚点(A_L;紫色)。
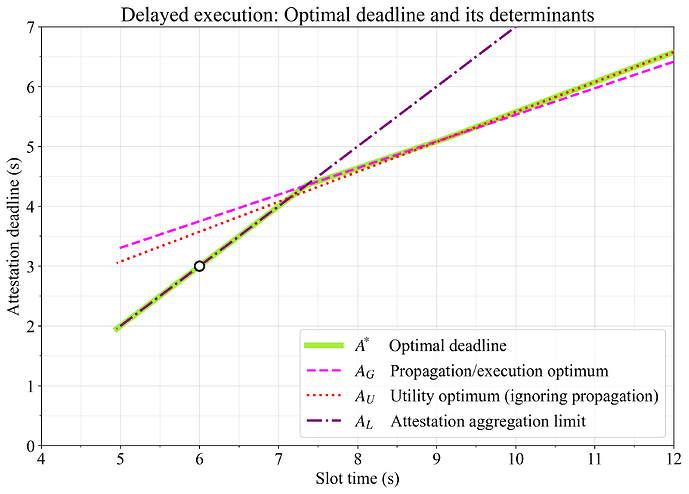
图 1. 在延迟执行中,最佳截止日期是传播/执行 gas 最优值 A_G,在纯粹受执行限制的模型中的效用最大值 A_U,以及允许 attestation 聚合的最晚点 A_L。 圆圈表示在 6s slot 中,attestation 截止日期为 3s 时的潜在目标。 为了获得最佳吞吐量,这将需要进行一些优化以改善传播时间(将优化的线向下推)。
使用默认常数,当 slot 为 12s 长时,最佳截止日期位于 6.5s 左右(A_U 机制)。 在低于约 9s 的 slot 时间下,Payload 传播时间限制了 blob 和执行的效用最优值,因此有必要通过选择较晚的 attestation 截止日期来妥协(A_G 机制)。 当 slot 时间降至约 7.3s 以下时,在 A_G 下不再有足够的时间进行 attestation 聚合,并且必须通过选择_较早的截止日期_来损害吞吐量(传播)(A_L 机制)。 在 6s slot 时间下,延迟执行的实现很可能以 3s attestation 截止日期为目标(正如已经 被提议)。 为了在 6s 时实现高吞吐量,有必要通过以下优化来加速传播(将图 1 中的优化线向下推):
- 使调用数据更加昂贵,
- 改善 p2p 层,
- 实施多维度费用市场或宏观定价(以限制最坏情况下的 Payload 大小)。
还可以假设 builder 本身可能会选择 Payload 组合,以平衡任何给定截止日期的传播和执行,从而为早期截止日期提供回旋余地。 但是,这将对具有较大字节大小的 Payload 造成 Payload 传播压力。 即使这些 Payload 符合 gaslimit,也可能无法被接受。 这是多维度费用市场如此有吸引力的原因之一。
ePBS
在对 ePBS 建模时,使用 双截止日期 方法,允许最佳 Payload PTC 截止日期 \mathrm{PTC}_P,同时保持 PTC DA 截止日期在 slot 的最晚可能点
$\mathrm{PTC}_B=S-\mathrm{PTC}_d.$
Payload 在一个无信任设置中发布,在最坏的情况下builder必须在 attestation 截止日期后的 A_d 发布 Payload。 附录 A 提供了在分析中包括 A_d 的相关性的讨论。 blob 的发布设置为 c,这样builder在发布 blob 之前不会等待 A_d 来计算 attestation,从而允许略长的传播时间。 在 ePBS 中,attestation 截止日期设置得比延迟执行早,具体来说,设置为常数 c:
$A = c = L_G + b_b L_D.$
然后 Payload 在 c+A_d 发布,并在传播时继承自己的全局延迟 L_G。 唯一剩下的任务是计算 Payload 的最佳 PTC 截止日期,\mathrm{PTC}_P,严格地将其确定为最大化总 gas G 的点。
gas 的数量受到执行窗口 S-\mathrm{PTC}_P 和执行速度 E_s (gas/s) 的限制:
$G \le E_s(S-\mathrm{PTC}_P).$
它还受到传播 Payload 所需时间的限制。 gas G 的 Payload 最多需要 LG + (G \cdot P{bg} \cdot L_D) 才能传播,并且必须允许最迟在 \mathrm{PTC}_P 截止日期之前到达:
$c + A_d + LG + (G \cdot P{bg} \cdot L_D) \le \mathrm{PTC}_P.$
这给出了传播的 gas 约束:
$G \le \frac{\mathrm{PTC}_P - c - A_d - LG}{P{bg}L_D}.$
最佳截止日期 \mathrm{PTC}^*_P 在 G 的两个限制相等时找到:
$E_s(S-\mathrm{PTC}_P) = \frac{\mathrm{PTC}_P - c - A_d - LG}{P{bg}L_D}.$
求解 \mathrm{PTC}_P 并用 \mathrm{PTC}_B 钳制,得到最终方程:
$\mathrm{PTC}^*_P = \min\Bigg(\mathrm{PTC}_B, \;\frac{c + A_d + L_G + Es P{bg} L_D S}{1 + Es P{bg} L_D}\Bigg).$
一旦找到最佳截止日期 \mathrm{PTC}^*_P,就可以确定最终吞吐量。 每秒 gas G_s 从传播约束得出:
$G_s = \frac{\mathrm{PTC}_P - c - A_d - LG}{P{bg}L_DS}.$
每秒 blob B_s 由可用于 blob 传播的时间决定,从它们在 c 的发布到 blob 截止日期 \mathrm{PTC}_B,同时考虑到它们自己的全局延迟 $L_G$,以及 blob 速率 B_r:
$B_s = \frac{(\mathrm{PTC}_B - c - L_G) \cdot B_r}{S}.$
图 2 显示了在基线常数下,在 ePBS 中最大化吞吐量的最佳截止日期。
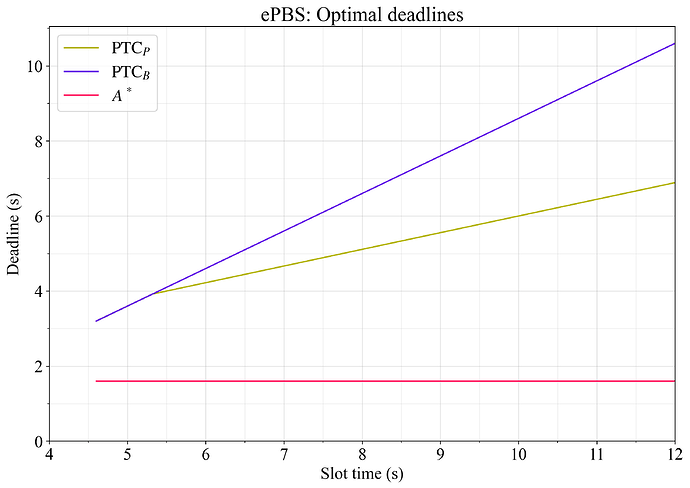
图 2. 在基线常数下,在 ePBS 中最大化吞吐量的最佳截止日期。 Payload 观察截止日期 $\mathrm{PTC}^*_P$ 设置在完美平衡传播和执行的点,遵守它不能在 PTC 投出其投票后发生的限制,即$ \mathrm{PTC}_B$。
延迟执行和 ePBS 的吞吐量
图 3 显示了延迟执行和 ePBS 的执行 Mgas/s 和 blobs/s。 显而易见,ePBS 特别适合扩展 blob,因为它提供了较晚的 PTC 截止日期。 由于可以独立设置 Payload 的截止日期,因此随着 slot 时间缩短,吞吐量会平稳衰减,直到传播最终限制在 5.5 秒以下。 由于以下因素的相对重要性增加,吞吐量平稳下降:
- 全局延迟 L_G,
- 信标区块传播时间 c,
- Builder 确信信标区块将收集到足够多的 attestation 所需的时间 A_d,
- 以及 PTC 投票传播时间 \mathrm{PTC}_d。
延迟执行最适合在较长的 slot 时间扩展 L1 gas,因为在 slot 开始时产生的延迟较少 L_G-L_R+A_d,并且使用默认常数可以在传播和执行之间合理地平衡 attestation 截止日期。 然后,当 attestation 聚合约束在大约 7.3 秒时起作用时,吞吐量曲线中会出现一个扭结。 由于在基线常数下传播时间不足,吞吐量大大低于此 slot 长度。
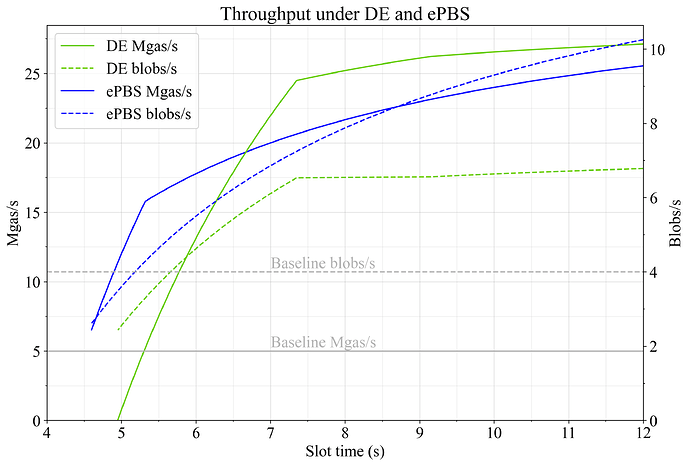
图 3. 在不同 slot 时间下,延迟执行(绿色)和 ePBS(蓝色)的吞吐量,指定为 Mgas/s(实线)和 blobs/s(虚线)。 即使在较短的 slot 时间下,这两种方法都有可能显着扩展 Ethereum。
根据 Glamsterdam 公式计算的效用
Glamsterdam 公式捕获了 slot 结构重组的扩展,其中考虑了 slot 时间 S^* 的相对变化以及捕获任何其他考虑因素的主观缩放因子 U_O。 如果优先考虑不更改分叉选择和没有 PTC 的简单性,则某人可能会为 DE 分配 U_O>1。 另一方面,如果例如,builder 和 proposer 之间的无信任支付被认为是至关重要的,那么某人可能会改为为 ePBS 分配 U_O>1。 完整方程为:
$U = (G^_s)^{U_G} \times (B^_s)^{U_B} \times (1/S^*)^{U_S} \times U_O.$
该方程还具有 效用弹性,它指定效用度量中不同性能指标的重要性。 1 的效用弹性表示效用与指标成正比,而 0 的弹性表示该指标与整体效用无关。 这些弹性包括:
- U_G – 执行吞吐量的效用弹性。
- U_B – blob 吞吐量的效用弹性。
- U_S – 较短 slot 时间的效用弹性。
图 4 显示了在设置 U_G=1、U_B=1、U_S=1 和 U_O=1 的情况下,延迟执行和 ePBS 的效用如何在 slot 时间内变化。 两种重组选项都给出了大致相等的效用增益,其中 DE 在 7.3 秒的 slot 时间达到峰值,而 ePBS 在 10 秒左右的 slot 时间达到峰值。
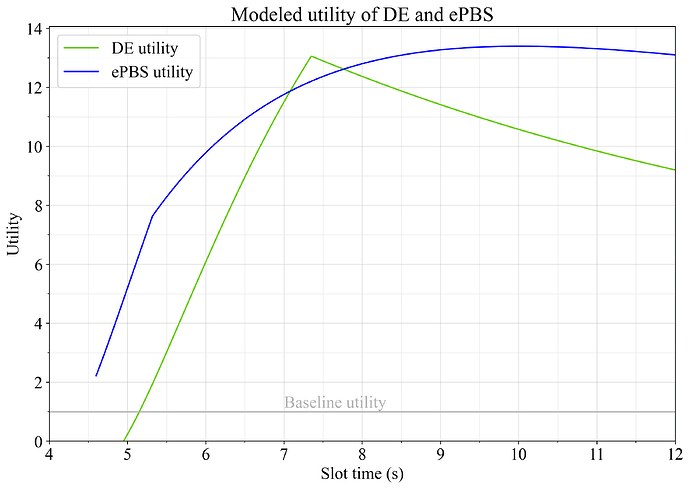
图 4. 当所有弹性都设置为 1 且两个选项的 U_O=1 时,延迟执行和 ePBS 的效用。
我们每个人对哪些指标最重要都有不同的看法,因此弹性非常有用。 例如,鉴于每个 slot 32 个 blob 的目标已经是 Fusaka 计划的显着改进,并且当前 6 个 blob 的目标实际上并未被消耗,因此似乎有理由为 blob 的进一步扩展分配比执行 gas 扩展要低的优先级。 U_G=1 和 U_B=0.4 的弹性捕获了这种概念。 在重要性方面,缩短 slot 时间可能会介于两者之间,例如 U_S=0.7。
图 5 显示了这些弹性的结果,这些弹性在某种程度上偏向于延迟执行,因为分配给 blob 扩展的重要性较低。 另一方面,有些人可能认为 ePBS 本质上更好,因为它能够促进builder和proposer之间的无信任合作。 为 ePBS 设置 U_O=1.1 捕获了 ePBS 在不可测量质量方面比延迟执行好 10% 的概念。 蓝色虚线捕获了这一点,并且效用最大化是使用在 9 秒左右的 slot 时间的 ePBS,还是使用在 7.3 秒的 slot 时间的 DE。
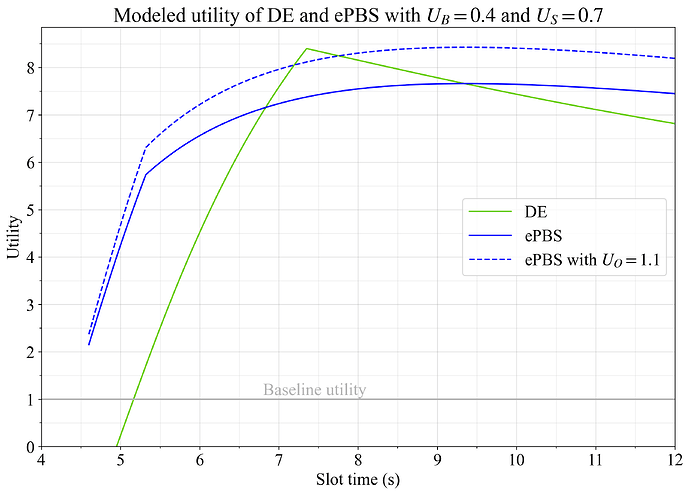
图 5. 具有弹性 U_G=1、U_B=0.4 和 U_S=0.7 的延迟执行和 ePBS 的效用。 蓝色虚线分配了 ePBS 比延迟执行的主观优势 10% (U_O=1.1)。
Gas 吞吐量扩展向量
图 6 回顾了主要扩展向量,重点关注 gas 吞吐量。 在此示例中,使用了上一节中相同的 U_B=0.4 设置,以允许延迟执行在设置 attestation 截止日期时,在某种程度上优先考虑 gas 吞吐量的增加而不是 blob 吞吐量的增加。
红色线表示如果执行速度从 60M gas/s 翻倍到 120M gas/s,吞吐量会增加。 在延迟执行中的较长 slot 时间下,这大大提高了吞吐量,因为可以花费更多的时间来传播更大的 Payload。 但是,在较短的 slot 时间下,吞吐量会像以前一样减少,因为那时更理想的 attestation 截止日期 A_G 和 A_U 都是不允许的,因为它们将位于 slot 的最后 3 秒内(参见图 1)。 因此,客户端无法使用所有可用的计算周期。 在某种程度上,可以通过重新定价以将传播替换为执行来解决此问题,如讨论中进一步概述的那样。 在 ePBS 中,attestation 传播的更理想条件意味着更快的执行在任何 slot 时间都是有用的,并且在 8 秒或更短的 slot 时间内已经超过了延迟执行的 gas 吞吐量。
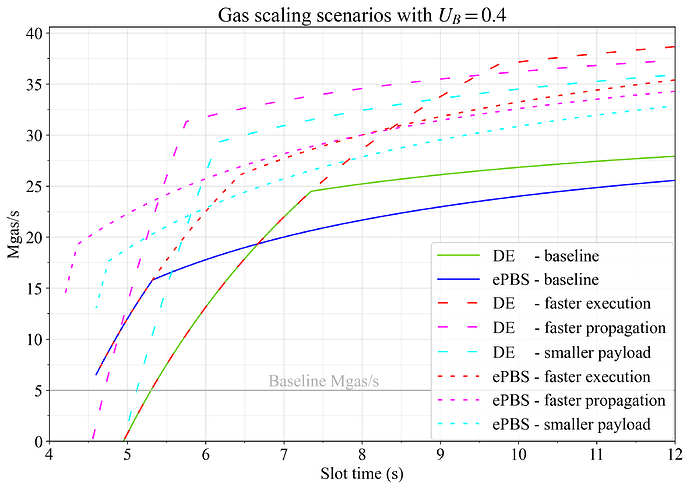
图 6. 在设置 U_G=1 和 U_B=0.4 时,主要扩展方案对 gas 吞吐量的影响。 分析了 DE 和 ePBS 的更快执行 (红色)、更快传播 (品红色) 和更小 Payload (青色),并与基线进行了比较。
品红色线表示使用设置 L_D=0.4 更快地传播信标区块和执行 Payload。 如果 U_B=1,即如果 blob 吞吐量被认为与执行吞吐量一样重要,那么对于延迟执行中的较长 slot 时间,品红色线将固定在绿线上。 发生这种情况是因为稍后的截止日期允许更多的 blob 传播。 当降低 blob 的优先级(如图所示)时,attestation 截止日期可以提前移动,并且执行吞吐量可以增加。 因此,快速传播允许在短 slot 时间下 DE 中非常有利的 gas 吞吐量,一直到 5.7 秒。 对于 ePBS,在所有 slot 时间都像以前一样稳定地改进,其中 \mathrm{PTC}_P 始终可以移动位置以最大化吞吐量。
青色线表示更小的 Payload,将 P_bg 设置为每 60M gas 0.5 MB。 每 60M gas 1 MB 的原始设置已经假设了一些 calldata 重新定价和对最突出异常值的限制。 然后需要进一步推进这一步,例如,使 calldata 更加昂贵。
图 7 显示了随着主要扩展向量的改进,blob 吞吐量如何变化。 随着传播速度的提高(品红色),ePBS 利用了信标区块和较早的 attestation 截止日期的更快传播来更早地发布 blob。 另一方面,延迟执行利用了更快的执行速度(红色),从而允许在较长的 slot 时间下的较晚的 attestation 截止日期。 请记住,延迟执行必须在 attestation 截止日期之前收到 blob,而 ePBS 可能会看到它们在 attestation 截止日期左右发布(在 mempool 中没有 blob 的情况下,builder 可能会提前发布一些 blob,并且可能希望等到截止日期之后再发布一些 blob)。
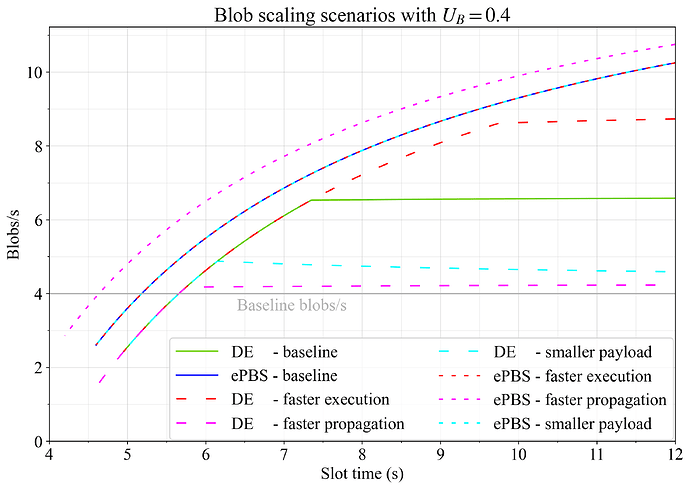
图 7. 在设置 U_G=1 和 U_B=0.4 时,主要扩展方案对 blob 吞吐量的影响。 分析了 DE 和 ePBS 的更快执行 (红色)、更快传播 (品红色) 和更小 Payload (青色),并与基线进行了比较。
对于更快的传播和更小的 Payload,DE 在 gas 吞吐量方面的大部分改进只能通过提前移动截止日期来为执行留出更多空间来实现。 然而,这不利于 blob 吞吐量,因此相对于效用最大值的 DE 基线有所下降,只是为了适应更快的吞吐量。 本文的最后一节回顾了具有 PTC 的 DE,其中此约束不再适用。 只有在相对较短的 slot 时间内,与 DE 基线相比,更快的传播才能提高 gas 吞吐量,而不会降低 blob 吞吐量(如下一个效用图所示)。 总的来说,ePBS 在 blob 吞吐量方面再次明显强于 DE,在所有可能的 slot 时间。
使用先前指定的弹性 U_G=1、U_B=0.4 和 U_S=0.7 计算了扩展向量的效用。 结果如图 8 所示。 快速传播是在两种情况下都在短 slot 时间内实现高实用性的关键。 至关重要的是,信标区块和 Payload 在 slot 的早期到达,以便为 attestation 聚合和执行留出时间。 因此,如果 Ethereum 要进一步扩展,那么对 p2p 层进行改进似乎很重要。 当然,对 attestation 聚合的改进同样有用(但是,3 秒的设置已经相当乐观了)。 图 9 通过高亮显示在不同未来扩展方案中每个 slot 时间的获胜流水线选项,总结了该发现。
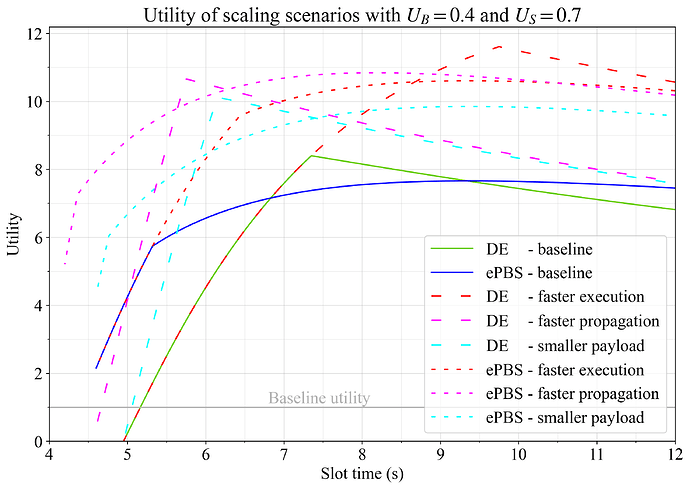 图 8. 当设置 U_G=1,U_B=0.4 和 U_S=0.7 时,主要扩容方案的效用。对 DE 和 ePBS 来说,更快的执行速度(红色)、更快的传播速度(品红色)和更小的有效载荷(青色)都进行了分析,并与基线进行了比较。
图 8. 当设置 U_G=1,U_B=0.4 和 U_S=0.7 时,主要扩容方案的效用。对 DE 和 ePBS 来说,更快的执行速度(红色)、更快的传播速度(品红色)和更小的有效载荷(青色)都进行了分析,并与基线进行了比较。
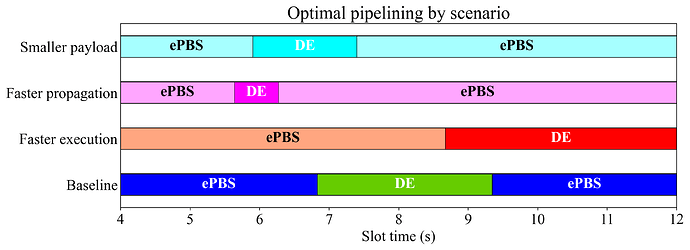
图 9. 当设置 U_G=1,U_B=0.4 和 U_S=0.7 时,DE 和 ePBS 在主要扩容方案之间的更高实用性。更快地执行(红色),更快地传播(品红色),更小的有效载荷(青色)以及基线都可视化了。
替代方案和障碍
图 10 显示了替代方案和障碍。青色框中概述了每个 60M gas 2 MB 的更大的有效载荷。这种有效载荷大小与当前的最坏情况一致,因此,如果没有进一步的数据成本增加,并且我们希望容纳仅填充 calldata 的区块,则此有效载荷大小将适用(如图所示,其效果还需要相对较慢的传播速度,如设置 L_D=0.8 所示)。如图所示,这将严重降低吞吐量。在这种情况下,我们可以考虑进一步重新定价数据、提高传播速度,或者限制对仅包含 calldata 的有效载荷的传播保证。这些有效载荷可以被认为是稍微“人为的”,因为它们与被认为是区块空间“正常”使用的情况相差太大,并且为这些异常值保留空间会整体上损害吞吐量。然后,这可以通过隐式方式完成,即设置一个非常严格的截止期限,以至于尝试传播这些有效载荷有时会导致区块丢失;或者通过显式方式完成,即通过宏观定价或完全限制这种使用模式。
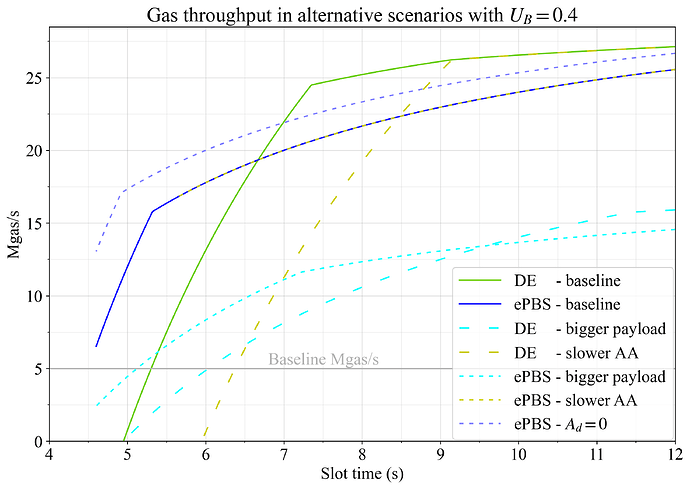
图 10. 当设置 U_G=1 和 U_B=0.4 时,替代方案对 gas 吞吐量的影响。对 DE 和/或 ePBS 来说,更大的有效载荷(青色)、更慢的 AA(黄色)和 A_d=0(蓝色虚线)都进行了分析,并与基线进行了比较。
黄色线表示较慢的证明聚合,设置为 4 秒。我们再次强调一个可能应该被认为是当今常态的场景。过去一个月,对证明聚合的分析一直指向不同的方向,但看起来 4 秒比 3 秒更接近当前的状态。在考虑 DE 的可行性时,证明聚合可以实现的速度非常重要,如图所示。我们能否将证明聚合降低到 3 秒?如果答案是否定的,那么短 slot 时间似乎相当令人生畏,除非我们还在 DE 中引入 PTC。下一个部分将介绍这种流水线变体。显而易见的是,除了使低于 5.6 秒的 slot 变得不可能之外,更长的 AA 不会对 ePBS 产生负面影响。
最后,浅蓝色虚线是 A_d=0 的 ePBS。这是 builder 始终可以在证明截止时间发布有效载荷的场景。在这种情况下,吞吐量显着增加。正如附录 A 中所讨论的,尚不完全清楚 A_d 的正确设置是什么。
图 11 显示了替代方案中的 blob 吞吐量,图 12 显示了最终的效用指标。可以注意到,当 builder 不需要 A_d 延迟来评估证明传播时,ePBS 在所有 slot 时间都比 DE 提供更高的吞吐量效用。
图 11. 当设置 U_G=1 和 U_B=0.4 时,替代方案对 blob 吞吐量的影响。对 DE 和/或 ePBS 来说,更大的有效载荷(青色)、更慢的 AA(黄色)和 A_d=0(蓝色虚线)都进行了分析,并与基线进行了比较。但是,这些替代设置都不会影响 ePBS 中的 blob 吞吐量,因此它们都重叠位于蓝线上。
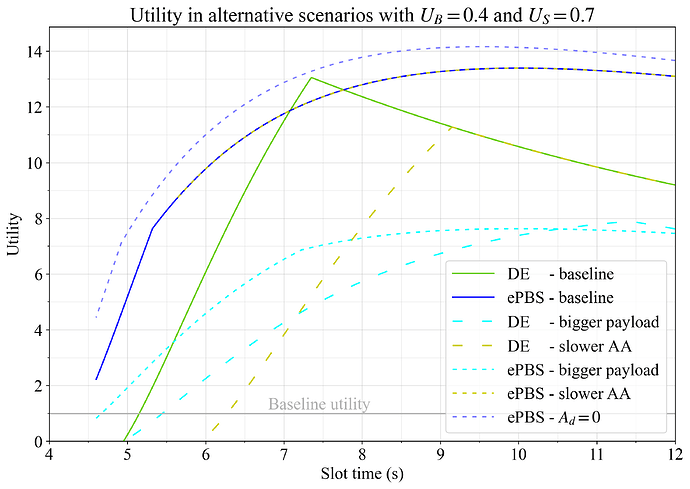
图 12. 当设置 U_G=1,U_B=0.4 和 U_S=0.7 时,替代方案中的效用。对 DE 和/或 ePBS 来说,更大的有效载荷(青色)、更慢的 AA(黄色)和 A_d=0(蓝色虚线)都进行了分析,并与基线进行了比较。
替代流水线变体
我们最终考虑替代规范。首先是使用 PTC 的延迟执行。在这种设计中,中继在 L_R 发布信标区块和有效载荷。证明截止日期设置得尽可能早,以允许证明聚合,并指示 p2p 层始终优先传播信标区块,以便 L_D 首先仅针对信标区块的大小进行计算,然后才针对有效载荷的大小进行计算。PTC 有效载荷截止时间 $\mathrm{PTC}_P$ 设置为最大化吞吐量,并且没有 A_d。
虽然优先于有效载荷传播信标区块使其能够更早到达,但似乎这种策略也会产生其自身的额外延迟,从而使信标区块和有效载荷的平均到达时间晚于 p2p 层不必尝试在两者之间制定传播策略时的情况,这是合理的。我们通过对信标区块和有效载荷施加额外的惩罚 L_P=0.3 来对此进行建模,因此它们的到达时间都比它们一起传播(或在没有优先级顺序的情况下单独传播,忽略变异性的影响)晚。但是,blob 已经在 L_R 发布并传播到 PTC 截止日期
$\mathrm{PTC}_B=S-\mathrm{PTC}_d.$
仅在证明聚合是阻碍因素的短 slot 时间内,产生优先传播延迟 L_P 才有益。因此,下图使用最佳传播策略,作为产生最高 gas 吞吐量的选项。因此,在优先考虑信标区块的选项中,证明截止时间设置为
$A = c = L_R + L_G + L_P + b_b L_D.$
这与之前的整体可行性约束 $S \ge c + A_a$ 一样,确保有足够的时间进行证明聚合。
就像在 ePBS 模型中一样,总 gas G 受两个条件的约束,这使我们能够找到最佳 PTC 有效载荷截止时间 $\mathrm{PTC}_P$。G 的两个条件可以设置为执行约束
$G \le E_s(S-\mathrm{PTC}_P)$
和传播约束,该约束考虑了有效载荷在时间 c 之后到达信标区块
$G \le \frac{\mathrm{PTC}P - c}{P{bg} L_D}.$
为了找到最大化吞吐量的最佳截止时间,我们将这两个绑定设置为相等,从而得出等式
$E_s(S-\mathrm{PTC}^_P) = \frac{\mathrm{PTC}^P - c}{P{bg} L_D}.$
求解 $\mathrm{PTC}^*_P$ 的该方程式得出最终表达式:
$\mathrm{PTC}^*_P = \min\Bigg(\mathrm{PTC}_B, \frac{c + Es P{bg} L_D S}{1 + Es P{bg} L_D}\Bigg).$
一旦确定了最佳截止时间 $\mathrm{PTC}^*_P$,就可以通过将该值代回传播约束中来计算最终 gas 吞吐量 G:
$G = \frac{\mathrm{PTC}^*P - c}{P{bg} L_D}.$
在不优先传播信标区块的选项中,证明截止时间和 $\mathrm{PTC}_P$ 而是根据以下条件设置的,其中截止时间 c 本身取决于产生的 gas G:
$A = \mathrm{PTC}_P = c = L_R + LG + (b\text{b} + P_{bg}G)L_D.$
将此条件与执行约束结合并求解 G,得出该场景中最佳 gas 的直接公式:
$G = \frac{E_s(S - L_R - L_G - b_bL_D)}{1 + EsP{bg}L_D}.$
如果从此均衡 gas 值导出的截止时间 c 对于证明聚合来说太晚了(即,c > S - A_a),则不会放弃该策略。相反,与延迟执行模型中的 A_L 钳位逻辑相呼应,截止时间被强制设置为最晚的允许时间 A_L = S - A_a。然后,将最终 gas 吞吐量重新计算为在此受约束的截止时间下执行和传播限制的最小值给出的新瓶颈。
用于使用 PTC 的延迟执行的相同分析可以用于 slot 拍卖 ePBS,其中拍卖在 slot 开始之前举行,并且 fork-choice 允许证明者投票选择空有效载荷(丢弃信标区块)。在这种(推测性)设计中,通过在先前的方程式中设置 L_R=0,也可以消除中继传播时间。
图 13-15 显示了 gas 和 blob 吞吐量以及 U_G=1,U_B=0.4 和 U_S=0.7 的效用。
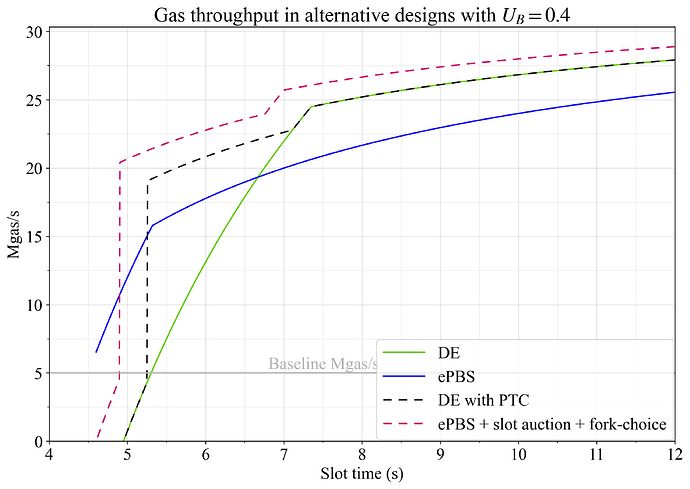
图 13. 在 DE 使用 PTC 或 ePBS 使用 slot 拍卖并允许证明者投票选择没有信标区块的有效载荷的替代设计中的 Gas 吞吐量。
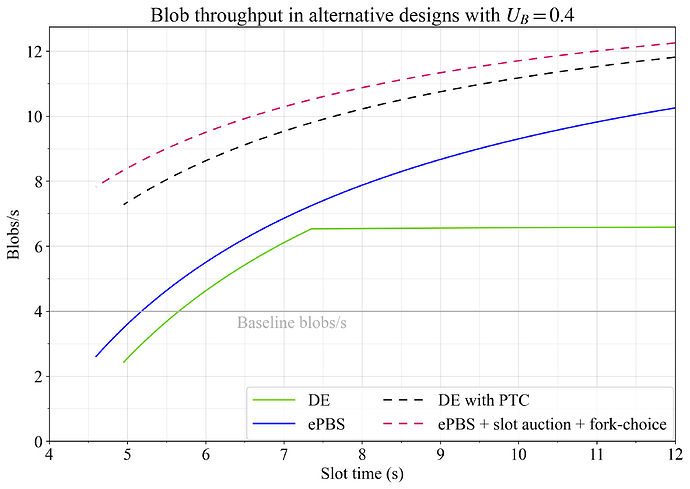
图 14. 在 DE 使用 PTC 或 ePBS 使用 slot 拍卖并允许证明者投票选择没有信标区块的有效载荷的替代设计中的 Blob 吞吐量。
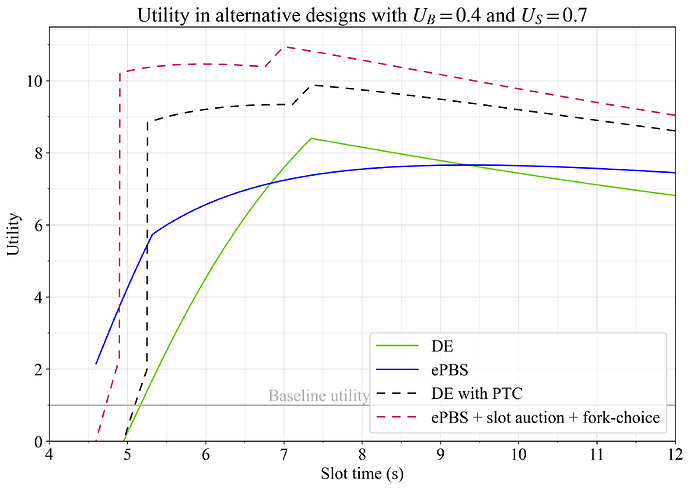
图 15. 当设置 U_G=1,U_B=0.4 和 U_S=0.7 时,在 DE 使用 PTC 或 ePBS 使用 slot 拍卖并允许证明者投票选择没有信标区块的有效载荷的替代设计中的效用。
结论与讨论
已经开发了延迟执行和 ePBS 中吞吐量的数学模型。这些模型用于分析吞吐量如何随 slot 时间变化,并在设置常量时依赖于基本假设。通过改变常量,分析了进一步优化以及潜在陷阱的影响。潜在的 slot 重新配置在短时间以及长时间的 slot 中都带来了显着的吞吐量提升。
选择哪种配置最终是一个效用问题。Glamsterdam 方程通过在所有 slot 时间为每个选项分配效用来对此进行建模。由于 DE 和 ePBS 必须在不同的约束条件下运行,因此并非所有 slot 时间都适合特定选项。一般来说,ePBS 在非常短的和相当长的 slot 时间特别好。在两者之间的窗口中,延迟执行可能通常更好,在该窗口中,有足够的时间进行证明聚合,并且早期信任地发布有效载荷的好处可以补偿 PTC 的缺失。执行窗口必须至少与证明聚合时间一样长。在短 slot 时间下,有效载荷传播的时间(相对于执行窗口)可能会变得太短。当然,同样的担忧也适用于 blob 传播的短时间。
在短 slot 时间下,一个普遍的关键问题是有效载荷传播。因此,改进 p2p 层应该具有很高的优先级。我们当然可以在某种程度上用定价来替代时间。鉴于执行速度的提高,如果之后的证明点不可行,我们可以重新定价以优先考虑执行。这涉及降低执行密集型操作的成本,并增加数据密集型操作(例如 calldata)的成本。从这个角度来看,如果从分析上讲,最佳证明截止日期被推入证明聚合区域,则执行速度的提高不一定会被浪费。因此,对证明截止日期的分析只能带我们走这么远,因为定价机制提供了单独的工具箱。
在类似的主题上,在其他条件相同的情况下,假设客户端也采用了 BAL,BAL 将会延迟最佳 DE 证明截止日期/ePBS PTC 有效载荷观察截止日期。关键是 BAL 会影响其他设计参数。图 9 表明了更快执行的影响,说明这特别有利于短 slot 时间下的 ePBS(而这两个选项在较长的 slot 时间下都有利)。另一方面,在 BAL 的背景下,图 10 显示,有效载荷大小的显着增加往往会严重降低吞吐量(在给定的传播速度假设下)。因此,即使对于 BAL 来说,保持合理的尺寸也是值得的。
最后需要注意的是,本文中用于 DE 和 ePBS 的两个主要设计规范不是重构 slot 的唯一方法。最后一节说明了在优化这些结构时,以增加复杂性为代价,可以进一步提高扩展性。
附录 A
在 ePBS 的非信任交换中,builder 无法指望 proposer 尽早发布信标区块,以便能够快速被证明。builder 必须提交一个有效载荷,并且在发现相对较晚发布的信标区块时,不能取消发布它所提交的确切有效载荷,这可能会使其成功。此外,它必须提防 proposer 的含糊不清,即使发布了有效载荷,也可能导致该有效载荷未被包含。因此,builder 有动机从证明时间开始稍微等待一下再发布有效载荷,并将附加一个值,以期望获得执行此操作的能力。
在 bid 时,builder 必须决定它愿意制作多大的有效载荷,并考虑到它可以使用的最坏情况传播窗口。由于非信任交换是一个区块拍卖,因此 builder 无法在事后决定其有效载荷的大小,并且倾向于不制作会使传播面临风险的有效载荷。因此,它应该合理地更喜欢构建可以在 A+A_d 和 $\mathrm{PTC}_P$ 之间充分传播的有效载荷。
在设计之间的比较中,我们修正了我们希望允许 builder 构建的每个 gas P{bg} 的有效载荷字节数,这与 gas G 一起给出了最大有效载荷字节大小 P{bg}G。如果截止时间太紧,以至于与 P{bg} 相对应的有效载荷无法传播,那么 builder 自然会通过构建较小的有效载荷来适应。但是,本文分析的目的是定义允许 P{bg}G 在分析设置中传播的截止时间。在 ePBS 中,该设置是非信任交换。仅将 ePBS 分析为非信任交换似乎确实有点不公平,因为 ePBS 流水线下的信任交换可以产生最高的整体吞吐量。
值得一提的是,在延迟执行中,builder 可以在从理论上讲,有效载荷可能太晚而无法与信标区块一起传播时取消其 bid。如果我们用 slot 拍卖代替区块拍卖来完成 ePBS,那么分析将更接近延迟执行中的 bid 调整。builder 可以根据其需要调整其有效载荷,并且从分析上讲,省略 Ad 变得更加直观。如果 builder 愿意,它仍然通常可以传播 P{bg}G,但不会承担相同的风险。读者可能对这些问题有不同的看法,因此本文介绍了有和没有 A_d 的结果。
- 原文链接: ethresear.ch/t/the-glams...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 深入探究 ENSv2 架构 46 浏览
- 以太坊怎么了? 34 浏览
- 以太坊 2026年协议级更新确定 3 大方向 272 浏览
- 寻找底线:为什么我们为 Layer 2 构建了紧急提款出口( Exit Hatch) 196 浏览
- 如何去中心化构建区块? 309 浏览
- Builder Codes & ERC-8021:修复链上归属问题 332 浏览
- 并行执行的谎言:为什么SOL和ZERO不是在与ETH竞争,而是在输给它的L2 372 浏览
- “夺旗”竞赛继续! 316 浏览
- EVM Gas 分析:新的执行跟踪数据 326 浏览
- 质押和链上信贷市场之间的微妙张力 434 浏览
- 以太坊的下一个重大转变:从重新执行每笔交易到验证 ZK 证明 381 浏览
- 以太坊应该停止担心扩展性,去做人们想要的东西 359 浏览
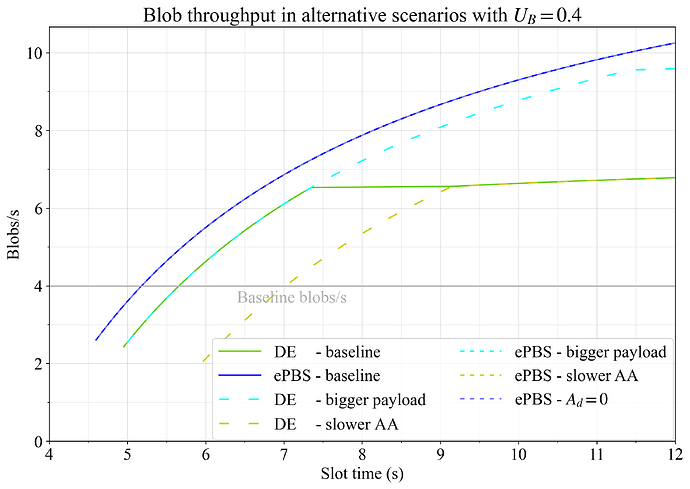 \
图 112563×1818 237 KB
\
图 112563×1818 237 KB
