以太坊邻近奖：Reed-Solomon码和MCA

以太坊邻近性奖（Ethereum Proximity Prize）：里德-所罗门码（Reed–Solomon Codes）与 MCA

以太坊基金会宣布了一项雄心勃勃的密码学赏金：高达 1.11 亿用于解决里德-所罗门码的接近上限（up-to-capacity proximity gaps）猜想，特别是其被称为互相关协议（mutual correlated agreement）的强化变体。

这听起来可能像是一个深埋在编码理论中的深奥问题，但其重要性不容小觑。这个数学猜想构成了现代零知识证明的基石，尤其是在基于哈希的 SNARK 中使用的 FRI 和 WHIR。这些证明系统对于以太坊的扩展路线图至关重要，能够在大规模上实现简洁且可验证的计算。

该猜想的解决将对整个区块链生态系统产生深远的影响。如果该猜想被证明为真，它将巩固已经构建到以太坊 zk-rollup 生态系统中的安全性和效率假设，确保当前的证明大小和计算成本在未来几年内保持可行。但是，如果该猜想被推翻，其后果可能很严重。它可能会使当前的效率声明失效，迫使证明大小显着增长，增加验证时间，并可能需要彻底重新设计整个类别的零知识协议。

本次探索将带你了解猜想本身，检查我们目前的理解，解释其密码学意义，并揭示为什么以太坊愿意投入大量资金来最终解决这个数学难题。

理解里德-所罗门码

线性码的构成要素

要理解为什么这个猜想很重要，我们需要从纠错码的基础知识开始。一个 $[n,k,\ell]_q$ 线性码 $C$ 代表一种复杂的数学结构：它是向量空间 $\mathbb{F}_q^n$ 中的一个 $k$ 维线性子空间，设计时在任何两个码字之间的最小距离为 $\ell$。

让我们分解一下每个参数的含义。块长度 $n$ 告诉我们每个码字在编码后的总长度。可以将其视为你实际传输的数据量，包括原始消息和纠错所需的冗余信息。

维度 $k$ 表示你要编码的原始消息符号的数量。由于 $C$ 在有限域 $\mathbb{F}_q$ 上构成一个 $k$ 维子空间，因此它包含精确的 $q^k$ 个唯一码字。比率 $\rho = k/n$ 给出了码的速率，该速率衡量了我们编码的效率：传输的数据中有多少携带了有用的信息，又有多少是冗余。

最小距离 $\ell$ 决定了代码的纠错能力。要理解这一点，我们首先需要考虑 $\mathbb{F}_q^n$ 中两个码字 $x$ 和 $y$ 之间的汉明距离。此距离 $d(x,y)$ 仅计算两个码字不同的坐标位置的数量。代码 $C$ 的绝对最小距离为

$d{\min}(C) = \min\{x \neq y \in C} d(x,y),$

并且我们经常使用相对最小距离

$d{\text{rel}}(C) = \frac{d{\min}(C)}{n}.$

对于线性码，我们将此最小距离表示为 $\ell$。

最后，$q$ 表示我们有限域的大小，本质上决定了我们的字母表。较大的域为我们提供了更大的灵活性，但也增加了计算复杂性。

里德-所罗门码的精妙之处

里德-所罗门码通过一个优雅的数学原理运作。我们从有限域 $\mathbb{F}_q$ 中 $n$ 个不同点的集合 $D = (\alpha_1, \ldots, \alpha_n)$ 开始，其中通常 $n \leq q$ 以确保我们有足够的的不同评估点。

编码过程将消息转换为多项式。我们获取消息并将其表示为小于 $k$ 次的多项式 $P(X)$ 的系数。然后在我们选择的 $n$ 个点处评估该多项式，从而创建 $n$ 个值。此评估过程是里德-所罗门编码的核心：我们本质上是对多项式进行过采样，通过在比唯一确定它严格需要的更多点上对其求值。

这种过采样创建了内置的冗余。即使某些评估点在传输过程中被破坏，只要我们不丢失太多值，我们仍然可以重建原始多项式（从而恢复我们的消息）。

一个具体的 RS 示例

• 域：$\mathbb{F}_{11}={0,\dots,10}$ （模 11 的算术）
• RS 码：长度 $n=7$，维度 $k=3$ ⇒ 次数 $<3$
• 域：$D={0,1,2,3,4,5,6}$
• 距离：$d_{\min}=n-k+1=5$

编码

选择一个次数 $<3$ 的消息多项式，例如

$$P(X)=3+4X+2X^2 \in \mathbb{F}_{11} [X].$$

在 $D$ 上求值：

$$ \begin{array}{c|ccccccc} x & 0 & 1 & 2 & 3 & 4 & 5 & 6\ \hline P(x) & 3 & 9 & 8 & 0 & 7 & 7 & 0 \end{array} $$

此向量 $[3,9,8,0,7,7,0]$ 是码字。

Singleton 界：一个基本限制

在编码理论中，我们编码信息的效率与我们可以纠正的错误数量之间存在一个基本的权衡。这种权衡由 Singleton 界 捕获，该界指出对于任何 $[n,k,\ell]_q$ 码，最小距离必须满足

$\ell \leq n-k+1.$

我们可以通过一个称为穿刺（puncturing）的巧妙论证来理解这个界限。想象我们有一个最小距离为 $\ell$ 的代码 $C$，这意味着任何两个不同的码字在至少 $\ell$ 个位置上不同。现在考虑如果我们从每个码字中删除前 $\ell - 1$ 个坐标会发生什么，从而创建一个穿刺映射 $\pi$，该映射获取 $n$ 坐标向量并生成 $(n-(\ell-1))$ 坐标向量。

关键的见解是，当限制于我们的代码时，此穿刺操作仍保持单射。如果两个原始码字 $c$ 和 $c'$ 不同，则它们在至少 $\ell$ 个位置上不同。在仅删除 $\ell - 1$ 个坐标后，至少必须保留一个不同的位置，因此 $\pi(c) \neq \pi(c')$。这意味着穿刺代码 $\pi(C)$ 具有与原始代码 $C$ 相同数量的码字。

但是，穿刺码字现在的长度为 $n-\ell+1$，并且在 $\mathbb{F}_q$ 上只有 $q^{\,n-\ell+1}$ 个可能的此长度的向量。由于 $|\pi(C)| = |C|$，我们必须有 $|C| \leq q^{\,n-\ell+1}$。对于 $|C| = q^k$ 的线性码，这给了我们 $k \leq n-\ell+1$，将其重新排列为 Singleton 界：

$\ell \leq n-k+1.$

这个界限背后的直觉很优雅。因为任何两个码字在至少 $\ell$ 个位置上不同，所以你可以擦除最多 $\ell-1$ 个坐标，并且码字仍然可区分。只有当你擦除 $\ell$ 个或更多坐标时，不同的码字才可能变得无法区分。这抓住了信息速率和纠错能力之间的基本张力。

为什么里德-所罗门码很特别

里德-所罗门码满足Singleton 界，有

$\ell = n-k+1.$

这使它们成为最大距离可分 (MDS) 码，代表了信息速率和纠错能力之间的最佳平衡。就这种基本权衡而言，实际上不可能比里德-所罗门码做得更好。

这种最优性是里德-所罗门码在实践中随处可见的原因，从 CD 播放器到卫星通信，再到现代密码协议。它们从每个冗余位中榨取最大的纠错能力，使其在保护数据免受损坏方面非常有效。

邻近性的语言

当我们收到一个可能已损坏的字时，我们需要确定它是否可能源自我们的代码。这需要引入精确的术语来衡量接收到的字与我们的代码有多“接近”。

对于任何固定的误差分数 $\delta$，我们可以根据接收到的字与最近码字的接近程度将其分为两类。

当至少存在一个码字 $u \in C$ 满足

$d(w,u) \leq \delta n.$

时，接收到的字 $w$ $\delta$-接近 代码 $C$。

在这种情况下，我们的候选列表是非空的，我们至少对接收到的字有一个合理的解释。

相反，当每个码字 $u \in C$ 满足

$d(w,u) > \delta n.$

时，接收到的字 $w$ $\delta$-远离 $C$。

在这里，我们的候选列表为空；没有码字位于我们可接受的误差半径内。

这个术语使我们能够清晰地提出基本的几何问题：给定一个接收到的字 $w$ 和误差容限 $\delta$，$w$ 是接近我们的代码还是远离它？

唯一解码半径和容量

因为任何两个不同码字之间的最小距离是 $\ell$，所以在它们有接触或重叠的风险之前，它们的保护气泡的半径可以达到（但不包括）$\ell/2$。这个关键值定义了代码的纠错限制。

代码保证可以纠正的最大错误数表示为 $t$，等于

$t = \left\lfloor \frac{\ell - 1}{2} \right\rfloor$

任何包含 $t$ 个或更少错误的接收到的字将始终比任何其他码字更接近原始码字。这个 $t$ 通常被称为代码的唯一解码半径。

几何直觉。考虑每个码字周围的半径为 $\ell/2$ 的汉明球。这些球是不相交的，因为中心之间的距离至少为 $\ell$。球内的任何 $w$ 都被唯一地解码到该球的中心；每个球外的点都是模棱两可的。

容量说明。将误差容限推向 $\ell/2$ 对应于接近Singleton 界 $\ell = n-k+1$：$\ell$ 越大（冗余越多），保证的唯一解码半径越大；速率 $\rho=k/n$ 越高，它越小。这是基本的速率-距离权衡。

拥抱歧义：一种更务实的方法

传统的唯一解码要求确定性，它坚持产生一个明确的答案。当面对歧义时，它只是失败，没有给我们留下任何有用的信息。列表解码采取了一种更务实的立场，提出了一个根本不同的问题：与其拼命寻找唯一正确的码字，为什么不提供一个简短的候选列表呢？

这种方法将我们的解码问题转化为更易于管理的问题。给定一个接收到的字 $w$，我们的目标是生成位于某个规定距离内的所有码字 $u \in C$。这种方法的优点不仅在于其灵活性，还在于其即使在不可能实现完全确定性的情况下也能保持有用。

出现的一个关键问题既明显又深刻：这个候选列表可能变得有多大？如果列表可以任意增长，那么我们提供一组可管理选项的承诺将变得毫无意义。这种担忧将我们带到了编码理论中最重要的理论结果之一：Johnson 界。

Johnson 界：数学与实践的结合

Johnson 界提供了一个通用的安全网，保证在某些条件下，我们的候选列表将保持小而易于管理。为了理解这个结果，我们需要从相对参数的角度来思考，这给了我们一个更清晰的视角来了解所涉及的基本权衡。

考虑相对最小距离

$\mu = \ell/n,$

它告诉我们代码固有的纠错能力。我们还定义了相对解码半径

$\delta = e/n,$

表示我们愿意容忍错误的符号位置的比例。

Johnson 界说明了一些非凡的事情：对于任何相对最小距离为 $\mu$ 的代码，以及对于任何接收到的字 $w$，只要满足以下条件，位于相对距离 $\delta$ 内的码字数量仍然受 $n$ 中多项式的限制，

$\delta < 1 - \sqrt{1 - \mu}.$

这个条件定义了我们所说的 Johnson 半径。在这个半径内，我们的候选列表保持小而易于管理，大小是多项式的。使该结果特别强大的是它的普遍性：该界限仅取决于基本参数 $\mu$ 和 $\delta$，而不取决于代码的具体结构。

对于大域上的里德-所罗门码，像 Guruswami-Sudan 这样复杂的算法可以实现列表解码，直到这个 Johnson 半径。由于里德-所罗门码具有 $\mu \approx 1-\rho$，其中 $\rho = k/n$ 是速率，因此 Johnson 半径变为

$\delta_J = 1 - \sqrt{\rho}.$

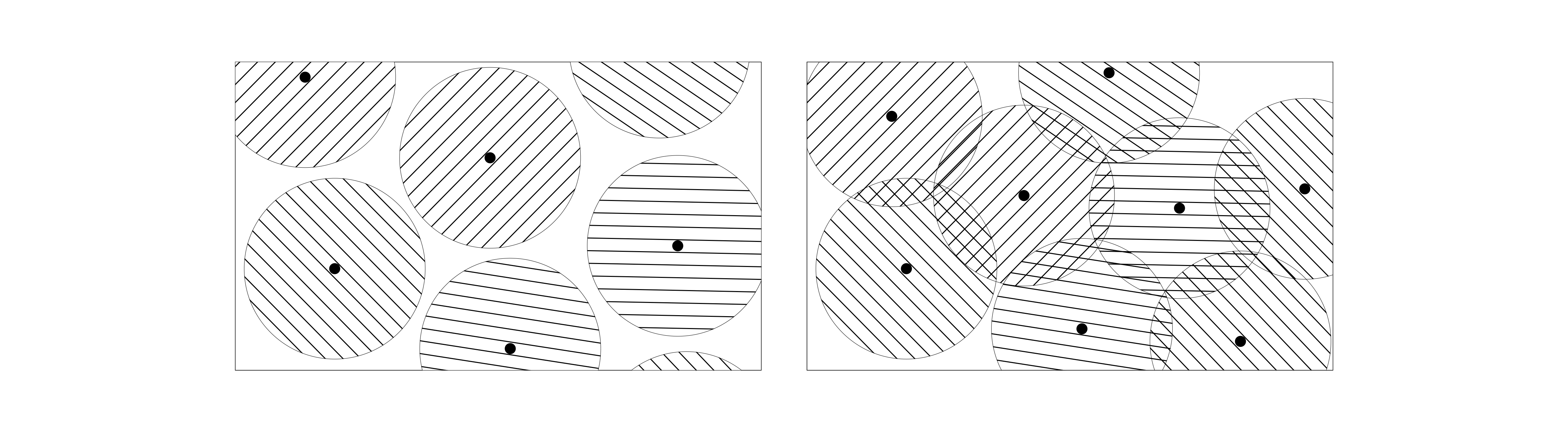
解码的三个世界

解码的格局自然地分为三个不同的区域，每个区域的特征在于我们试图处理的错误比例 $\delta$。

唯一解码的安全区 发生在

$\delta < \mu/2.$

在这里，我们仍然处于舒适的世界中，在任何接收到的字的解码半径内最多可以存在一个码字。这是传统经典纠错的领域，算法简单且答案明确。

列表解码的领域 出现在

$\mu/2 \leq \delta < 1 - \sqrt{1-\mu}.$

我们已经离开了唯一性的安全区，但我们还没有进入混乱状态。Johnson 界保证我们的候选列表仍然很小，并且值得注意的是，存在有效的算法来查找该范围内的所有候选对象。用于里德-所罗门码的 Guruswami-Sudan 算法例证了复杂的数学如何驯服最初看起来难以解决的问题。

组合荒野 开始于

$\delta \geq 1 - \sqrt{1-\mu}.$

在这里，潜在候选者的数量可能会呈指数级增长，使得对通用代码进行解码在计算上不可行。该区域代表了多项式时间算法可能实现的基本限制。

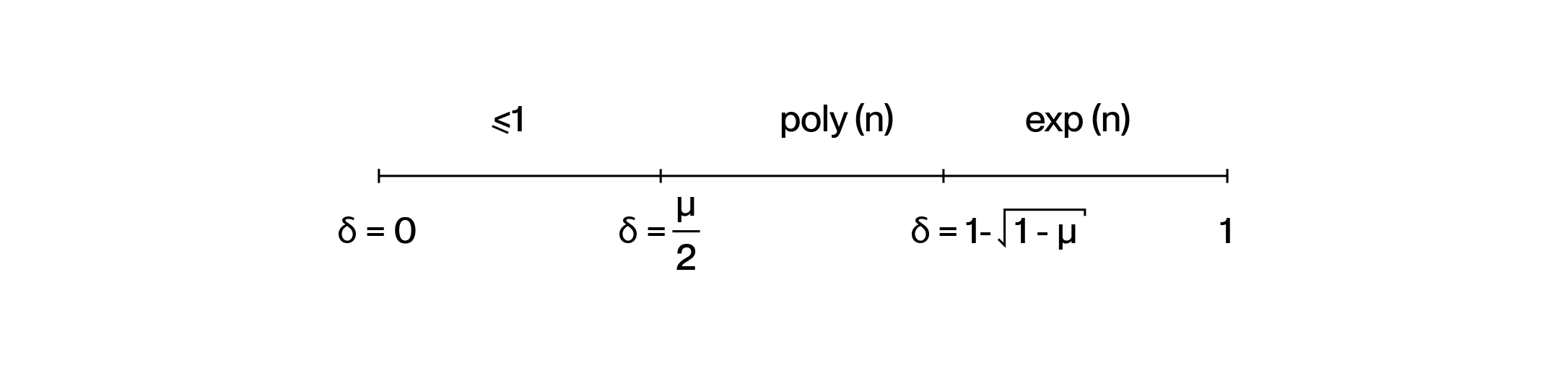
邻近性测试和间隙现象

想象一下，你是一个验证者，试图检查一堆向量是否是有效的码字。单独检查每一个？这将非常昂贵。因此，这里有一个密码学家喜欢的聪明技巧：不单独测试每个向量，而是要求证明者将它们混合成一个随机线性组合：

$u' = r_0 u_0 + r_1 u_1 + \cdots + r_t u_t, \qquad r_i \in \mathbb{F}_q.$

现在你只需要测试这一个组合向量 $u'$，看看它是否 $\delta$ 接近你的里德-所罗门码。非常简洁的优化，对吧？但这里有一个价值百万美元的问题：这个快捷方式真的有效吗？如果即使其中一个原始向量 $u_i$ 是垃圾（意味着 $\delta$ 远离代码），随机组合 $u'$ 是否仍然会以高概率看起来很糟糕？

事实证明，答案涉及到一个叫做邻近性间隙的美妙数学现象。

结构化集合的全有或全无性质

在计算机科学中，我们喜欢“间隙”——事物干净利落地落入两个桶中的一种情况，没有混乱的中间地带。想想经典的例子，如 PCP 定理（你的公式要么是可满足的，要么就是非常难以满足的）或使用 Miller-Rabin 进行的素数测试。

在这里，我们正在研究“成为有效的里德-所罗门码字”这个属性，当我们查看结构化的输入集合时，我们将看到这种间隙行为的出现——特别是 $\mathbb{F}_q^n$ 的仿射子空间。

让我们具体一点。采用里德-所罗门码 $V = \mathrm{RS}_q(D,k) \subseteq \mathbb{F}_q^n$，该码由在大小为 $n$ 的某个域 $D$ 上评估的次数小于 $k$ 的多项式构建。现在考虑 $\mathbb{F}_q^n$ 的子集的集合 $\mathcal{S}$ ——通常是仿射子空间，如直线或平面。

如果 $\mathcal{S}$ 中的每个子集 $S$ 都以两种极端方式之一运行，那么我们说 $\mathcal{S}$ 相对于 $V$ 具有 $(\delta,\varepsilon)$- 邻近性间隙：

• 全有： $S$ 中的每个向量都接近代码：

$\Pr_{u\in S}[d(u,V)\le \delta n] = 1$

• 全无： $S$ 中几乎没有向量接近：

$\Pr_{u\in S}[d(u,V)\le \delta n] \le \varepsilon$

$\varepsilon$ 越小，这种全有或全无的行为就越明显。

我们实际了解的关于里德-所罗门码的知识

这是使所有这些实用的主要结果。对于速率为 $\rho = k/n$ 的里德-所罗门码 $V = RS_q(D,k) \subseteq \mathbb{F}_q^n$，我们获得高达著名的 Johnson 半径 $1 - \sqrt{\rho}$ 的误差分数 $\delta$ 的邻近性间隙。所有仿射子空间的集合表现出 $(\delta,\varepsilon)$ 邻近性间隙，其中 $\varepsilon$ 取决于我们所在的区域：

• 唯一解码区（当 $0 < \delta < \dfrac{1-\rho}{2}$ 时）：

$\varepsilon \;=\; \varepsilon_U(q,n) \;=\; \frac{n}{q}.$

• Johnson 区（当 $\dfrac{1-\rho}{2} \le \delta < 1-\sqrt{\rho}$ 时）：

如果我们定义安全裕度 $\eta := (1-\sqrt{\rho})-\delta > 0$，则：

$\varepsilon \;\le\; O!\left(\frac{n^{2}}{\,q\,(\eta\,\rho)^{O(1)}}\right).$

为什么要关心？ 这完全证明了我之前提到的随机线性组合技巧的合理性。选择随机系数 $r_i \in \mathbb{F}_q$ 并形成 $u'=\sum_i r_i u_i$。如果你的任何输入向量 $u_i$ $\delta$ 远离代码，那么以至少 $1-\varepsilon$ 的概率，你的组合 $u'$ 也会 $\delta$ 远离代码。一个测试可以捕获所有内容！

一些技术说明

• 关于 $\delta$ 范围： 最大值 $\delta = 1-\sqrt{\rho}$ 不是任意的——它正是 Johnson/Guruswami-Sudan 列表解码半径。有些人怀疑间隙现象可能会进一步延伸（可能一直到容量界限 $1-\rho$），但这仍然是一个猜想。

• 字段大小很重要： 为了使 Johnson 区域能够干净地工作，你需要 $q$ 大致是 $n$ 的二次方（考虑 $q \gtrsim n^2$）。但对于唯一解码区域，$q = \Theta(n)$ 就足够了。

• 这些界限很紧： 尤其是在唯一解码的情况下，$\varepsilon = n/q$ 界限基本上已经达到了最佳状态。确实存在仿射线，它们不会给你更强有力的结果。

相关协议：当接近不仅仅是运气

这里有一个有趣的见解：假设你取两个向量并形成大量的随机线性组合，并且这些组合中的许多碰巧看起来接近你的里德-所罗门码。这种接近不可能是由于错误的幸运抵消造成的——一定存在一些深刻的结构在起作用。具体来说，必须存在一个大的坐标集，其中两个原始向量已经与你的代码中的一些码字相符。这种共享结构就是我们所说的相关协议。

基本设置

让我们使用我们在评估域 $D$ 上构建的里德-所罗门码 $V = RS_q(D,k) \subseteq \mathbb{F}_q^n$。我将把码字视为 $D$ 上的函数，因此 $u \in \mathbb{F}_q^D$。我们将使用 $d(\cdot,\cdot)$ 表示汉明距离，并写 $d(u,V)$ 表示 $u$ 到最近码字的距离。 固定你的邻近性参数 $\delta$ 和我们刚刚讨论的邻近性 간극 定理中的误差参数 $\varepsilon$。

它的工作原理

取两个向量 $u_0, u_1 \in \mathbb{F}_q^D$ 并查看它们生成的仿射线：

$A = { u_0 + z \cdot u_1 : z \in \mathbb{F}_q }$.

现在假设这条线上很大一部分点 $\delta$ 接近代码：

$\Pr_{z \in \mathbb{F}_q} [ d(u_0 + z u_1, V) \le \delta n ] > \varepsilon$.

然后发生了非凡的事情：必须存在一个大的子域 $D' \subset D$ 和实际的码字 $v_0, v_1 \in V$，使得：

• 大多数坐标都很好：

$\frac{|D'|}{|D|} \ge 1 - \delta$

• 这两个向量与这些坐标上的代码一致：

$u0|{D'} = v0|{D'} \quad \text{and} \quad u1|{D'} = v1|{D'}$

用简单的英语来说：如果 $u_0 + z u_1$ 的许多组合看起来接近你的代码，那是因为 $u_0$ 和 $u_1$ 都在一个 公共的 大部分坐标上与一些码字一致。

一般情况

这自然地扩展到更高维的仿射空间。取向量 $u_0, u1, \ldots, u\ell \in \mathbb{F}_q^D$ 并考虑：

$U = u_0 + \mathrm{span}{u1, \ldots, u\ell } \subset \mathbb{F}_q^D$.

如果 $U$ 中有足够的点接近代码（大于 $\varepsilon$ 部分），则存在一个大的坐标集 $D'$，其中所有生成器 $u0, \ldots, u\ell$ 同时与相应的码字 $v0, \ldots, v\ell$ 一致。

为什么这很重要

相关协议为我们提供了我们想要的邻近性间隙的充分条件。直观地说，如果一批线性组合经常看起来很接近代码，那么只有当所有底层向量都与代码共享一个大的“协议区域”时才有可能。 最大的未解之谜？我们不知道相关一致性对于邻近间隙是否也是必要的。也许还有其他方法可以在约翰逊半径之外获得间隙（对于 $\delta > 1-\sqrt{\rho}$），而无需通过这种一致性结构。

间隙定理自然成立

一旦你有了相关一致性，邻近间隙定理几乎变得显而易见。每条线 $A$ 都属于以下两种类别之一：

• 完全包含 (All-in): $A$ 上的每个点都 $\delta$-接近代码（当 $A$ 在一个大的坐标集上与某个代码行一致时，就会发生这种情况）。
• 完全排除 (All-out): $A$ 上最多只有 $\varepsilon$ 分数的点是 $\delta$-接近的。

相互相关一致性：更上一层楼

对于现代密码学协议来说，事情变得非常有趣。像 WHIR 这样的系统不仅仅每轮检查单个随机线性组合。它们创建相同基础向量的几种不同的混合——想想折叠操作、移位、不同的组合模式。为了在将所有这些检查批量处理在一起时保持严格的可靠性，你需要比普通相关一致性更强大的东西。

你需要相同的大坐标集来同时在你的整个混合操作系列中证明一致性。这就是相互相关一致性 (MCA)。

总体思路

设 $\mathcal{M}$ 是你的验证者在给定轮次中使用的一系列仿射线性混合操作。对于每个操作 $M \in \mathcal{M}$，假设你有：

$\Pr_{\theta} [\Delta(M(\theta), V) \le \delta] \ge \varepsilon_M$

对于混合参数 $\theta$ 的一些合理的度量。

相互相关一致性推测认为应该存在一个单一的坐标集 $D' \subseteq D$，其中 $|D'| \ge (1-\delta)n$ 以及一个一致的码字族，使得对于所有 $M \in \mathcal{M}$ 和所有参数 $\theta$ 同时成立：

$M(\theta)|{D'} \in V|{D'}$

关键词是“相互”——一个通用的“好的”坐标集 $D'$，适用于你的整个混合族，而不是每个操作单独的集合。

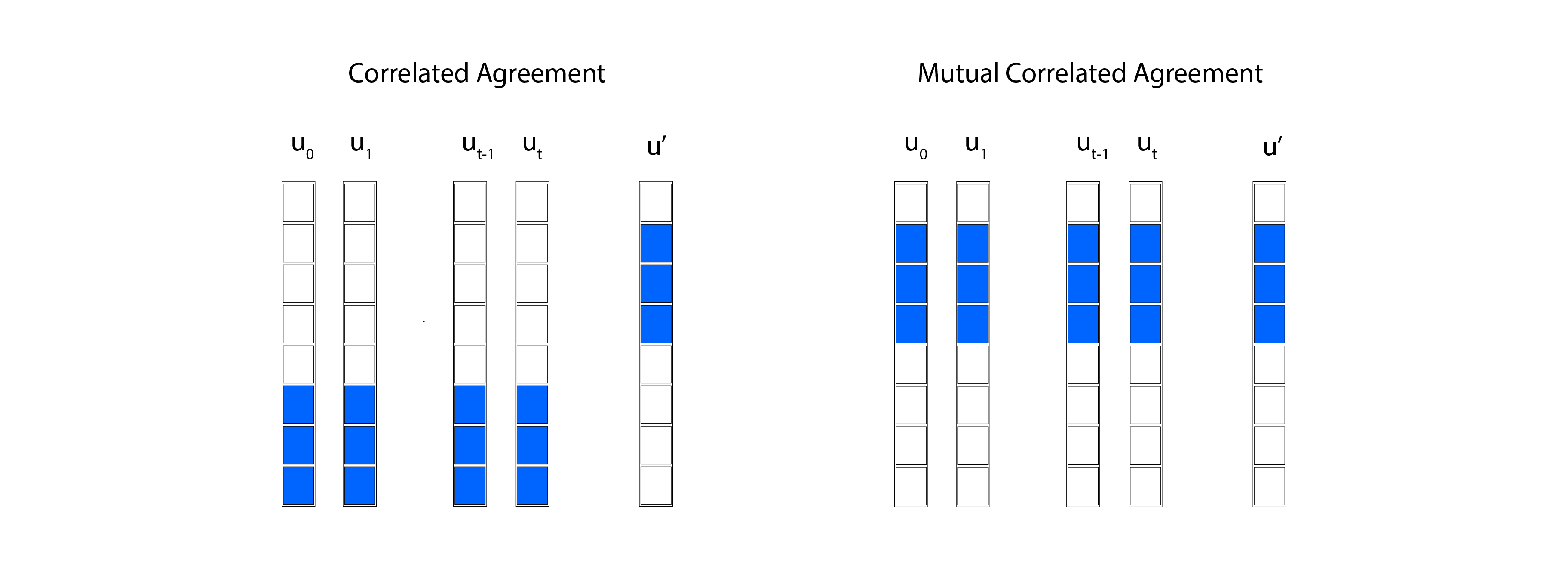
我们的立场

• 已证明对于唯一解码： 当 $\delta < (1-\rho)/2$ 时，WHIR 论文建立了 MCA，这使得他们在每轮批量处理多个检查时能够实现“无可靠性下降”的结果。

• 一个大的猜想： 将 MCA 扩展到约翰逊区域 ($\delta < 1-\sqrt{\rho}$) 甚至更远（在 $\delta < 1-\rho$ 处达到“达到容量”）现在是该领域的核心开放问题之一。

• 为什么这很重要： 证明将为最快的基于透明 Reed–Solomon 的协议提供尽可能严格的可靠性分析。反例将迫使我们重新设计参数或协议。

结论

以太坊基金会的百万美元赏金不仅仅是一项数学挑战，更是对可扩展区块链基础设施的密码学基础的战略投资。Reed-Solomon 码的相互相关一致性猜想位于纯粹数学和实用密码学的交叉点，理论突破直接转化为现实世界的影响。

我们的探索揭示了为什么这个特定的猜想如此重要。Reed-Solomon 码已经在信息率和纠错之间提供了最佳的权衡（达到 Singleton 界），使其成为密码学协议的自然选择。邻近间隙现象允许同时高效地批量验证多个语句，从而显着降低零知识证明的计算开销。但是，为了将这些效率推向其理论极限，尤其是在执行复杂混合运算的 WHIR 等协议中，我们需要相互相关一致性提供的更强的保证。

风险显而易见。积极的结果将验证以太坊扩展路线图背后的安全假设，确认当前的 zk-rollup 架构可以在扩展到全球采用时保持其效率保证。数学证明将表明，批量验证技术可以一直推到约翰逊半径（或可能甚至达到容量界限），而不会牺牲可靠性。

相反，负面的结果将迫使我们从根本上重新评估我们如何设计透明的零知识协议。证明的大小可能需要增加，验证时间可能会增加，并且整类的优化可能会被证明是不健全的。密码学社区将需要开发在反例揭示的任何限制范围内工作的新方法。

致谢

本次探索建立在编码理论、密码学和复杂性理论中无数研究人员的基础工作之上。 Reed-Solomon 码邻近间隙的理论基础在 "Reed–Solomon 码的邻近间隙" 中得到了全面的处理，该文献确立了我们在约翰逊半径和相关一致性现象探索中讨论的许多基本结果。 实际的密码学应用和相互相关一致性猜想在 "WHIR：具有超快速验证的 Reed–Solomon 邻近性测试" 中有详细说明，该文献的作者将这种数学瓶颈确定为在批量验证协议中实现最佳可靠性的关键。 我们特别感谢以太坊基金会的 Thomas Coratger 在该领域所做的持续工作，包括他关于邻近性证明的 综合存储库，该存储库提供了有价值的教学材料，有助于我们进行阐述。

• 原文链接： hexens.io/blog/proximity...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～