第 4 章. 密码学

以太坊的基础技术之一是密码学，它是计算机安全中广泛使用的一个数学分支。密码学在希腊语中意为“秘密写作”，但密码学的研究范围不仅仅是秘密写作，秘密写作被称为加密。 例如，密码学也可以用来证明对秘密的了解而不泄露该秘密（例如，使用数字签名），或者证明数据的真实性（例如，使用数字指纹，也称为哈希）。 这些类型的密码学证明是 以太坊平台（实际上，所有区块链系统）运行的关键数学工具，并且在以太坊应用程序中也被广泛使用。

请注意，在发布时，以太坊协议的任何部分都不涉及加密； 也就是说，与以太坊平台以及节点之间的所有通信（包括交易数据）都是未加密的，并且（必须）可以被任何人读取。 这样做是为了让每个人都可以验证状态更新的正确性，并且可以达成共识。 将来，零知识证明和同态加密等高级密码学工具将可用，这些工具将允许在区块链上记录一些加密计算，同时仍然能够实现共识； 然而，虽然已经为它们做了准备，但尚未完全部署。

在本章中，我们将介绍以太坊中使用的一些密码学，即公钥密码学 (PKC)，它以私钥和地址的形式用于控制资金的所有权。

密钥和地址

正如我们在本书前面学到的，以太坊有两种不同类型的帐户：EOA 和合约。 EOA 对以太币的所有权是通过数字私钥、以太坊地址和数字签名建立的。 私钥是用户与以太坊所有交互的核心。 事实上，帐户地址直接从私钥派生而来：私钥唯一确定一个以太坊地址，也称为帐户。

私钥不会以任何方式直接在以太坊系统中使用； 它们永远不会被传输或存储在以太坊上。 也就是说，私钥应保持私密，永远不应出现在传递给网络的消息中，也不应存储在链上； 只有帐户地址和数字签名会被传输和存储在以太坊系统中。 有关如何安全可靠地保管私钥的更多信息，请参阅“钱包最佳实践”。

对资金的访问和控制是通过数字签名实现的，数字签名也是使用私钥创建的。 以太坊交易需要有效的数字签名才能包含在区块链中。 任何拥有私钥副本的人都可以控制相应的帐户及其持有的任何以太币。 假设用户对其私钥进行安全保管，则以太坊交易中的数字签名会证明资金的真正所有者，因为它们证明了私钥的所有权。

在基于 PKC 的系统中（例如以太坊使用的系统），密钥以成对的形式出现，包括私有（秘密）密钥和公钥。 将公钥视为类似于银行帐号，将私钥视为类似于秘密 PIN； 后者提供对帐户的控制，而前者向其他人标识该帐户。 以太坊用户很少看到私钥本身； 在大多数情况下，它们以加密形式存储在特殊文件中，并由以太坊钱包软件管理。

在以太坊交易的支付部分，预期的收件人由以太坊地址表示，其使用方式与银行转帐的收款人帐户详细信息相同。 正如我们将很快更详细地看到的那样，EOA 的以太坊地址是从密钥对的公钥部分生成的。 但是，并非所有以太坊地址都代表公钥 - 私钥对； 它们也可以表示合约，正如我们将在第 7 章中看到的那样，合约没有私钥的支持。

在本章的其余部分，我们将：

• 更深入地研究密码学的基础知识，并探讨其在以太坊中的数学基础
• 检查密钥生成、存储和管理的过程
• 查看用于私钥、公钥和地址的各种编码格式
• 调查验证者密钥密码学和 KZG 承诺方案，它们代表以太坊密码学基础设施的最新更新

PKC 和加密货币

PKC（也称为非对称密码学）是现代信息安全的核心组成部分。 由 Martin Hellman、Whitfield Diffie 和 Ralph Merkle 于 1970 年代首次发布的密钥交换协议是一项具有里程碑意义的突破，激发了公众对密码学领域的第一次巨大兴趣。 在 1970 年代之前，强大的密码学知识被政府保密。

PKC 使用唯一的密钥来保护信息。 这些密钥基于具有特殊属性的数学函数：很容易计算它们，但很难计算它们的逆。 基于这些函数，密码学可以创建数字秘密和不可伪造的数字签名，这些签名受到数学定律的保护。

例如，简单地将两个大的素数相乘。 但是，给定两个大素数的乘积，很难找到素数因子（称为素数分解）。 假设我们提供数字 8,018,009 并告诉您它是两个素数的乘积。 对于您来说，找到这两个素数比我将它们相乘得到 8,018,009 要困难得多。

如果您知道一些秘密信息，这些数学函数中的一些可以很容易地逆转。 在前面的示例中，如果我告诉您其中一个素数因子是 2,003，则您可以使用简单的除法轻松找到另一个素数因子：8,018,009 ÷ 2,003 = 4,003。 这样的函数通常称为陷门函数，因为除非您获得一条秘密信息，可以用作反转该函数的快捷方式，否则很难反转它们。

一类更有用的密码学高级数学函数基于椭圆曲线上的算术运算。 在椭圆曲线算术中，模素数的乘法很简单，但除法（逆运算）实际上是不可能的。 这被称为离散对数问题，并且目前没有已知的陷门。 椭圆曲线密码学广泛用于现代计算机系统，并且是以太坊（和其他加密货币）使用私钥和数字签名的基础。

注意

如果您有兴趣阅读更多关于密码学以及现代密码学中使用的数学函数，请查看以下资源：

• 密码学
• 陷门函数
• 素数分解
• 离散对数
• 椭圆曲线密码学

在以太坊中，我们使用 PKC 创建我们在本章中一直在讨论的公钥 - 私钥对。 它们被认为是“一对”，因为公钥是从私钥派生的。 它们共同代表一个以太坊帐户，分别提供一个可公开访问的帐户句柄（地址）和对帐户中任何以太币以及使用智能合约时帐户需要的任何身份验证的私有控制。 私钥通过成为创建数字签名所需的唯一信息来控制访问，数字签名需要对交易进行签名才能花费帐户中的任何资金。 数字签名也用于验证合约的所有者或用户身份，我们将在第 7 章中看到。

提示

在大多数钱包实现中，为了方便起见，私钥和公钥作为密钥对存储在一起。 但是，公钥可以从私钥直接计算出来，因此也可以仅存储私钥。

可以创建数字签名来签名任何消息。 对于以太坊交易，交易本身的详细信息用作消息。 密码学的数学原理（在本例中为椭圆曲线密码学）提供了一种将消息（即交易详细信息）与私钥组合以创建只能通过了解私钥才能生成的代码的方法。 该代码称为数字签名。

请注意，以太坊交易基本上是访问具有特定以太坊地址的特定帐户的请求。 当交易被发送到以太坊网络以便转移资金或与智能合约交互时，需要使用数字签名发送，该数字签名是使用与所讨论的以太坊地址对应的私钥创建的。 椭圆曲线数学意味着任何人都可以通过检查数字签名是否与交易详细信息以及请求访问的以太坊地址匹配来验证交易是否有效。 验证根本不涉及私钥； 它保持私密。 但是，验证过程毫无疑问地确定交易只能来自拥有以太坊地址背后公钥对应的私钥的人。 这就是 PKC 的“魔力”。

提示

以太坊协议中没有加密，作为以太坊网络运行的一部分发送的所有消息都可以（必须）被所有人读取。 因此，私钥仅用于为交易身份验证创建数字签名。

私钥

私钥只是一个随机选择的数字。 私钥的所有权和控制权是用户控制与相应以太坊地址关联的所有资金以及访问授权该地址的合约的根本所在。 私钥用于创建签名，通过证明交易中使用的资金的所有权来花费以太币。 私钥必须始终保持秘密，因为将其透露给第三方相当于将其控制的由该私钥保护的以太币和合约控制权交给他们。 私钥还必须备份并防止意外丢失。 如果丢失，则无法恢复，并且由其保护的资金也将永远丢失。

提示

以太坊私钥只是一个数字。 随机选择私钥的一种方法是简单地使用硬币、铅笔和纸：抛掷硬币 256 次，您就拥有了一个随机私钥的二进制数字，您可以在一个以太坊钱包中使用它（可能 - 请参阅以下几段）。 然后，可以从私钥生成公钥和地址。

生成密钥的第一步也是最重要的一步是找到一个安全的熵或随机性来源。 创建一个以太坊私钥本质上涉及选择一个介于 1 和 2^256 之间的数字 。 您用来选择该数字的确切方法并不重要，只要它是不可预测的或确定性的。 以太坊软件使用底层操作系统的随机数生成器 (RNG) 来生成 256 个随机位。 通常，OS RNG 由人类随机源初始化，这就是为什么您可能会被要求摆动鼠标几秒钟或在键盘上按随机键。 替代方法可能是计算机麦克风通道上的宇宙辐射噪声。

更确切地说，私钥可以是任何非零数字，最大为一个非常大的数，略小于 2^256——一个巨大的 78 位数字，大约为 1.158 × 10^77。 确切的数字与 2^256 共享前 38 位数字，并被定义为以太坊中使用的椭圆曲线的阶数。 为了创建一个私钥，我们随机选择一个 256 位数字，并检查它是否在有效范围内。 在编程术语中，这通常通过将一个更大的随机位字符串（从密码安全的随机源收集）输入到一个 256 位哈希算法中来实现，例如 Keccak-256 或 SHA-256，这两个算法都会方便地生成一个 256 位数字。 如果结果在有效范围内，我们就有一个合适的私钥。 否则，我们只需使用另一个随机数重试。

注意

以太坊的私钥空间的大小——2^256——是一个难以想象的巨大数字。 它在十进制中约为 10^77——也就是说，一个有 78 位数字的数字。 相比之下，据估计可见宇宙包含 10^80 个原子。 因此，几乎有足够的私钥给宇宙中的每个原子一个以太坊帐户。 如果您随机选择一个私钥，那么没有人会猜到它或自己选择它。

请注意，生成私钥的过程是一个离线过程； 它不需要与以太坊网络进行任何通信——或者实际上，与任何人进行任何通信。 因此，为了选择一个其他人永远不会选择的数字，它需要是真正随机的。 如果您自己选择这个数字，那么其他人会尝试它（然后带着您的以太币逃跑）的可能性太高了。 使用一个糟糕的 RNG（比如大多数编程语言中的伪随机 rand 函数）甚至更糟糕，因为它更明显，更容易复制。 就像在线帐户的密码一样，私钥需要是不可猜测的。 幸运的是，您永远不需要记住您的私钥，所以您可以采取最佳方法来选择它：真正的随机性。

警告

不要编写自己的代码来创建一个随机数，或者使用您的编程语言提供的“简单”RNG。 请注意，除非由操作系统熵支持，否则浏览器钱包中基于 JavaScript 的 RNG 可能不安全。 至关重要的是，您要使用密码安全的伪随机数生成器（例如 CSPRNG），该生成器使用来自具有足够熵的源的种子。 研究您选择的 RNG 库的文档，以确保它是密码安全的。 CSPRNG 库的正确实现对于密钥的安全性至关重要。

以下是以十六进制格式显示的随机生成的私钥（256 位显示为 64 个十六进制数字，每个 4 位）：

f8f8a2f43c8376ccb0871305060d7b27b0554d2cc72bccf41b2705608452f315

公钥

以太坊公钥是椭圆曲线上的一个点，这意味着它是一组满足椭圆曲线方程的 x 和 y 坐标。

简单来说，以太坊公钥是两个连接在一起的数字。 这些数字是通过只能单向运行的计算从私钥生成的。 这意味着如果你有私钥，计算公钥是微不足道的，但是你不能从公钥计算私钥。

警告

数学即将发生！ 不要惊慌。 如果您在接下来的几段中开始迷失方向，您可以跳过接下来的几个部分。 有许多工具和库可以为您完成数学运算。

公钥是使用椭圆曲线乘法从私钥计算出来的，这实际上是不可逆的：K = k * G，其中k是私钥，G是一个称为生成点的常数点，K是生成的公钥，而*是特殊的椭圆曲线“乘法”运算符。 请注意，椭圆曲线乘法与普通乘法不同。 它与普通乘法共享功能属性，但仅此而已。 例如，反向操作（对于普通数字来说是除法），称为“查找离散对数”——也就是说，如果您知道K，则计算k——与尝试k的所有可能值（一种蛮力搜索，可能需要比这个宇宙允许的时间更长的时间）一样困难。

简单来说，椭圆曲线上的算术与“常规”整数算术不同。 一个点 (G) 可以乘以一个整数 (k) 以生成另一个点 (K)。 但是没有除法这样的东西，所以不可能简单地将公钥 K "除以"点 G 来计算私钥 k。 这是前面“PKC 和加密货币”部分中描述的单向数学函数。

注意

椭圆曲线乘法是密码学家称为“单向”函数的一种函数：它在一个方向（乘法）上很容易，而在相反方向（除法）上不可能。 私钥的所有者可以很容易地创建公钥，然后与世界分享，并且知道没有人可以反转该函数并从公钥计算私钥。 这种数学技巧成为不可伪造且安全的数字签名的基础，这些签名证明了以太坊资金的所有权和对合约的控制。

在我们演示如何从私钥生成公钥之前，让我们更详细地了解一下椭圆曲线密码学。

椭圆曲线密码学解释

椭圆曲线密码学是一种基于离散对数问题的非对称或公钥密码学，如椭圆曲线点的加法和乘法所表达的。 图 4-1 是一个椭圆曲线的例子，类似于以太坊使用的椭圆曲线。

注意

以太坊使用与比特币完全相同的椭圆曲线，称为secp256k1。 这使得可以重用比特币中的许多椭圆曲线库和工具。

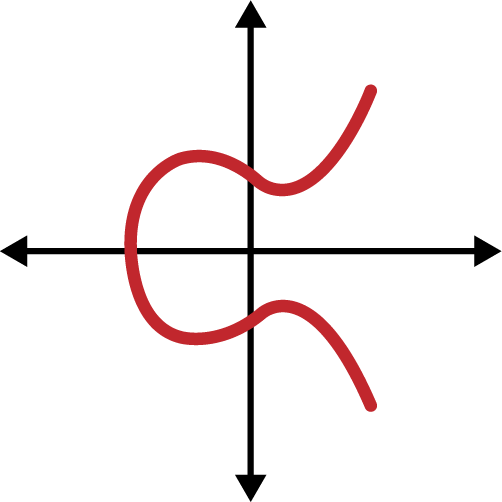
图 4-1. 一个椭圆曲线

以太坊使用特定的椭圆曲线和一组数学常量，如美国国家标准与技术研究院 (NIST) 建立的名为secp256k1的标准中所定义。 secp256k1曲线由以下函数定义，该函数生成椭圆曲线：

y^2 = (x^3 + 7) over (Fp)

或者：

y^2 mod p = (x^3 + 7) mod p

mod p（模素数 p）表示该曲线在素数阶 p 的有限域上，也写为 Fp，其中 p = 2^256 – 2^32 – 2^9 – 2^8 – 2^7 – 2^6 – 2^4 – 1，这是一个非常大的素数。

因为这个曲线定义在素数阶的有限域上，而不是在实数上，所以它看起来像一个分散在二维空间中的点阵，这使得它很难可视化。 但是，其数学原理与实数上的椭圆曲线的数学原理相同。 例如，图 4-2 显示了在小得多的素数阶 17 的有限域上的相同椭圆曲线，显示了网格上的点阵。 可以将 secp256k1 以太坊椭圆曲线视为一个不太可知的大网格上一个更复杂的点阵。

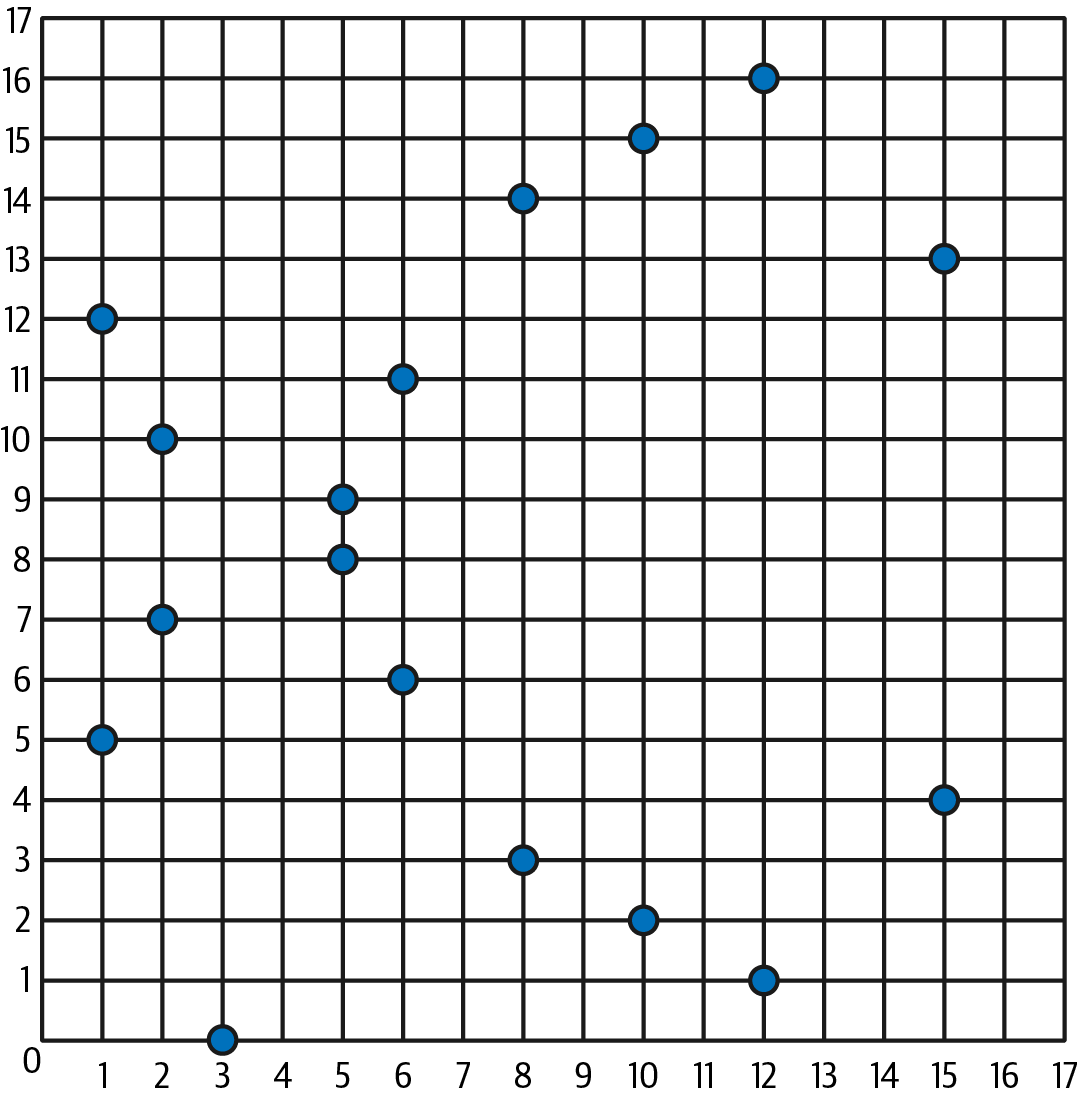
图 4-2. 椭圆曲线密码学：可视化在 F(p) 上的椭圆曲线，其中 p=17

因此，例如，以下是坐标为 (x, y) 的点 Q，它是 secp256k1 曲线上的一个点：

Q = (49790390825249384486033144355916864607616083520101638681403973749255924539515, 59574132161899900045862086493921015780032175291755807399284007721050341297360)

例 4-1 展示了如何使用 Python 亲自检查这一点。 变量 x 和 y 是点 Q 的坐标，如前面的例子中的那样。 变量 p 是椭圆曲线的素数阶（用于所有模运算的素数）。 Python 的最后一行是椭圆曲线方程（Python 中的 % 运算符是模运算符）。 如果 x 和 y 确实是椭圆曲线上一个点的坐标，那么它们满足方程且结果为零。 通过在命令行上键入 python（或 python3）并从列表中复制每一行（在提示符 >>> 之后）来亲自尝试一下。

例 4-1. 使用 Python 确认该点在椭圆曲线上

Python 3.12.4 (main, Jun  6 2024, 18:26:44) [Clang 15.0.0 (clang-1500.3.9.4)] on darwin
Type "help", "copyright", "credits" or "license" for more information.
>>> p = 115792089237316195423570985008687907853269984665640564039457584007908834671663
>>> x = 49790390825249384486033144355916864607616083520101638681403973749255924539515
>>> y = 59574132161899900045862086493921015780032175291755807399284007721050341297360
>>> (x ** 3 + 7 - y**2) % p
0

椭圆曲线算术运算

许多椭圆曲线数学看起来与我们在学校学到的整数算术非常相似。 具体来说，我们可以定义一个加法运算符，该运算符不是沿着数字线跳跃，而是跳到曲线上的其他点。 一旦我们有了加法运算符，我们还可以定义点和整数的乘法，这等同于重复加法。

椭圆曲线加法定义为：给定椭圆曲线上的两个点 P1 和 P2，则存在第三个点 P3 = P1 + P2，该点也在椭圆曲线上。

从几何上讲，通过绘制 P1 和 P2 之间的线来计算第三个点 P3。 这条线将恰好在另一个位置与椭圆曲线相交（非常神奇）。 将此点称为 P3′ = (x, y)。 然后在 x 轴中反射以获得 P3 = (x, –y)，如图 4-3 所示。

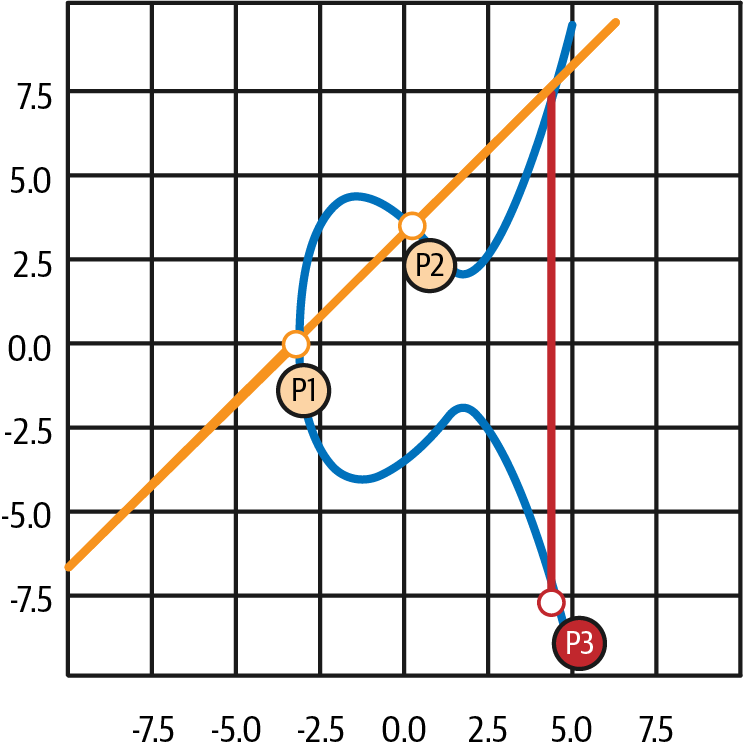
图 4-3. 椭圆曲线加法：在椭圆曲线上添加两个点

如果 P1 和 P2 是同一个点，则 "之间" P1 和 P2 之间的线应该延伸为该点 P1 处的曲线的切线。 该切线将恰好在另一个新点与曲线相交，如图 4-4 所示。 您可以使用微积分中的技术来确定切线的斜率。 奇怪的是，这些技术有效，即使我们将注意力限制在曲线上具有两个整数坐标的点上！

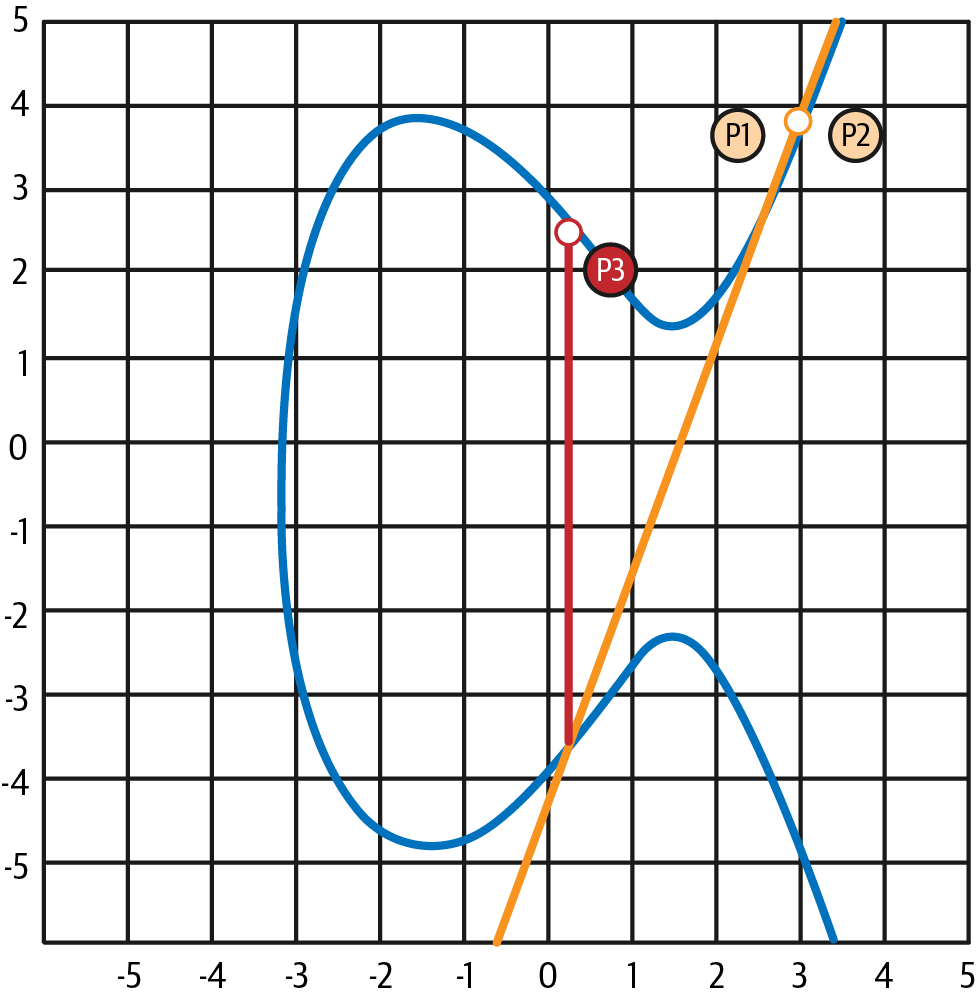
图 4-4. 椭圆曲线加法：将一个点添加到自身

在椭圆曲线数学中，还有一个称为无穷远点的点，它大致对应于加法中数字零的作用。 在计算机上，它有时用 x = y = 0 表示（这不满足椭圆曲线方程，但它是一个容易检查的独立情况）。 有几个特殊情况解释了对无穷远点的需求。

在某些情况下（例如，如果 P1 和 P2 具有相同的 x 值但不同的 y 值，如图 4-5 所示），该线将是完全垂直的，在这种情况下，P3 = 无穷远点。

图 4-5. 椭圆曲线加法：导致无穷远点的特殊情况

如果 P1 是无穷远点，则 P1 + P2 = P2。 类似地，如果 P2 是无穷远点，则 P1 + P2 = P1。 这表明无穷远点如何在“正常”算术中发挥零的作用。

事实证明，+ 是关联的，这意味着 (A + B) + C = A + (B + C)。 这意味着我们可以毫无歧义地编写 A + B + C（没有括号）。

现在我们已经定义了加法，我们可以按照扩展加法的标准方法定义乘法。 对于椭圆曲线上的点 P，如果 k 是一个整数，则 k * P = P + P + P + … + P（k 次）。 请注意，在这种情况下，k 有时（可能令人困惑）被称为指数。

生成公钥

从以随机生成的数字 k 形式的私钥开始，我们将它乘以曲线上一个预先确定的点，称为生成点 G，以生成曲线上的另一个点，即相应的公钥 K：

K = k * G

生成点是作为secp256k1标准的一部分指定的； 对于secp256k1的所有实现都是相同的，并且从该曲线派生的所有密钥都使用相同的点G。 因为对于所有以太坊用户来说，生成点始终相同，所以私钥k乘以G将始终导致相同的公钥K。 k 和 K 之间的关系是固定的，但只能在一个方向上计算，从 k 到 K。 这就是为什么可以与任何人共享一个以太坊地址（从 K 派生），并且不会泄露用户的私钥 (k)。

正如我们在上一节介绍的那样，k * G 的乘法等效于重复加法，因此是 G + G + G + … + G，重复 k 次。 总而言之，要从私钥 k 生成公钥 K，我们将生成点 G 加到它自身，k 次。

提示

私钥可以转换为公钥，但公钥不能转换回私钥，因为数学运算只在一个方向上有效。

让我们应用这个计算来找到我们在 “私钥” 部分中向您展示的特定私钥的公钥：

K = f8f8a2f43c8376ccb0871305060d7b27b0554d2cc72bccf41b2705608452f315 * G

密码学库可以帮助我们使用椭圆曲线乘法计算 K。 生成的公钥 K 定义为点：

K = (x, y)

其中：

x = 6e145ccef1033dea239875dd00dfb4fee6e3348b84985c92f103444683bae07b
y = 83b5c38e5e2b0c8529d7fa3f64d46daa1ece2d9ac14cab9477d042c84c32ccd0

在 以太坊 中，您可能会看到公钥表示为 130 个十六进制字符（65 个字节）的序列化。 这是从行业联盟高效密码学标准 (SECG) 提出的标准序列化格式中采用的，该格式记录在 高效密码学标准 (SEC1) 中。 该标准定义了可以用来识别椭圆曲线上点的四种可能的序列化前缀，如表 4-1 所示。

表 4-1. 序列化的椭圆曲线公钥前缀

前缀	含义	长度（字节，包括前缀）
0x00	无穷远点	1
0x04	未压缩的点	65
0x02	具有偶数 y 的 压缩点	33
0x03	具有奇数 y 的 压缩点	33

以太坊只使用未压缩的公钥，所以唯一相关的前缀是（十六进制）04。 序列化 连接公钥的 x 和 y 坐标：

04 + x 坐标 (32 字节 / 64 十六进制) + y 坐标 (32 字节 / 64 十六进制)

因此，我们之前计算的公钥序列化为：

046e145ccef1033dea239875dd00dfb4fee6e3348b84985c92f103444683bae07b83b5c38e5e2b0c8529d7fa3f64d46daa1ece2d9ac14cab9477d042c84c32ccd0

椭圆曲线库

secp256k1椭圆曲线有一些实现，用于加密货币相关的项目中：

OpenSSL

OpenSSL 库提供了一套全面的基本加密功能，包括 secp256k1 的完整实现。 例如，为了导出一个 公钥，可以使用函数 EC_POINT_mul。

libsecp256k1

Bitcoin Core 的 libsecp256k1 是 secp256k1 椭圆曲线和其他密码学原语的 C 语言实现。 它是从头开始编写的，用于替换 Bitcoin Core 软件中的 OpenSSL，并且在性能和安全性方面都被认为更优越。

密码学哈希函数

密码学哈希函数在整个以太坊中使用。 事实上，哈希函数被广泛用于几乎所有的密码学系统中 —— 密码学家 Bruce Schneier 抓住了这个事实，他说，“与其说是加密算法，还不如说单向哈希函数是现代密码学的核心。”

在本节中，我们将讨论哈希函数，探讨其基本属性，并了解这些属性如何使其在现代密码学的许多领域中如此有用。 我们在这里讨论哈希函数，因为它们是以太坊公钥转换为地址的一部分。 它们还可以用于创建数字指纹，这有助于验证数据。

简单来说，哈希函数是任何可用于将任意大小的数据映射到固定大小的数据的函数。 哈希函数的输入称为原像、消息，或者简称为输入数据。 输出称为哈希。 密码学哈希函数是一个特殊的子类别，它具有特定的属性，这些属性对于保护以太坊等平台很有用。

密码学哈希函数是一种单向哈希函数，它可以将任意大小的数据映射到固定大小的比特字符串。 “单向” 的性质意味着，如果一个人只知道输出哈希，则在计算上不可行地重新创建输入数据。 确定可能的输入的唯一方法是执行蛮力搜索，检查每个候选对象以获得匹配的输出； 鉴于搜索空间实际上是无限的，因此很容易理解任务的实际不可能。 即使您找到一些创建匹配哈希的输入数据，它也可能不是原始输入数据：哈希函数是“多对一”函数。 查找两个哈希到相同输出的输入数据集称为查找哈希冲突。 粗略地说，哈希函数越好，哈希冲突就越少。 对于 以太坊 来说，它们实际上是不可能的。

让我们仔细看看密码学哈希函数的主要属性：

确定性

给定的输入消息总是产生相同的哈希输出。

可验证性

计算消息的哈希是高效的（线性复杂度）。

非相关性

对消息的小修改（例如，1 位修改）应该会广泛地更改哈希输出，使其无法与原始消息的哈希相关联。

不可逆性

从消息的哈希计算消息是不可行的，等效于对所有可能的消息进行蛮力搜索。

碰撞保护

计算两个产生相同哈希输出的不同消息应该不可行。

抵抗哈希碰撞对于避免以太坊中的数字签名伪造尤为重要。

这些属性的组合使密码学哈希函数适用于广泛的安全应用，包括：

• 数据指纹识别
• 消息完整性（错误检测）
• 工作量证明
• 身份验证（密码哈希和密钥拉伸）
• 伪随机数生成器
• 消息承诺（提交-揭示机制）
• 唯一标识符

当我们逐步了解系统的各个层时，我们将在 以太坊 中找到许多这些应用。

以太坊密码学哈希函数：Keccak-256

以太坊在许多地方使用 Keccak-256 密码学哈希函数。 Keccak-256 被设计为 NIST 于 2007 年举办的 SHA-3 密码学哈希函数竞赛的候选者。 Keccak 是获胜算法，于 2015 年标准化为联邦信息处理标准 (FIPS) 202。

然而，在开发以太坊期间，NIST 标准化尚未最终确定。 NIST 据称修改了 Keccak 的一些参数，以提高其效率，从而完成了标准流程。 与此同时，英雄般的举报人 Edward Snowden 泄露了文件，暗示 NIST 可能受到了美国国家安全局的不当影响，从而故意削弱了 Dual_EC_DRBG RNG 标准，从而有效地在该标准 RNG 中植入了一个后门。 这一争议的结果是对拟议变更的强烈反对，并导致 SHA-3 标准化进程的重大延误。 当时，以太坊基金会决定实现其发明者提出的原始 Keccak 算法，而不是 NIST 修改的 SHA-3 标准。

警告

虽然您可能会在整个以太坊文档和代码中看到提及“SHA-3”，但许多（如果不是全部）这些实例实际上指的是 Keccak-256，而不是最终的 FIPS-202 SHA-3 标准。 实现上的差异很小，与填充参数有关，但很重要的一点是，对于相同的输入，Keccak-256 产生的哈希输出与 FIPS-202 SHA-3 不同。

我正在使用哪个哈希函数？

如果您使用的软件库同时可能被称为 “SHA-3”，您如何判断它是否实现了 FIPS-202 SHA-3 或 Keccak-256？

一个简单的方法是使用测试向量，即给定输入的预期输出。 用于哈希函数的测试最多的是空输入。 如果您使用空字符串作为输入运行哈希函数，您应该看到以下结果：

Keccak256("") = c5d2460186f7233c927e7db2dcc703c0e500b653ca82273b7bfad8045d85a470
SHA3("") = a7ffc6f8bf1ed76651c14756a061d662f580ff4de43b49fa82d80a4b80f8434a

无论函数名称如何，您都可以通过运行这个简单的测试来测试它是否是原始的 Keccak-256 还是最终的 NIST 标准 FIPS-202 SHA-3。 请记住，以太坊使用 Keccak-256，即使它在代码中经常被称为 SHA-3。

注意

由于以太坊中使用的哈希函数 (Keccak-256) 与最终标准 (FIP-202 SHA-3) 之间的差异造成的混乱，所有代码、操作码和库中所有 sha3 实例都已重命名为 keccak256。 详见 ERC-59。

接下来，让我们检查 Keccak-256 在以太坊中的第一个应用，即从公钥生成以太坊地址。

以太坊地址

以太坊地址是唯一的标识符，它们是使用 Keccak-256 单向哈希函数从公钥或合约派生的。

在我们之前的示例中，我们从一个私钥开始，并使用椭圆曲线乘法来派生一个公钥。

私钥 k:

k = f8f8a2f43c8376ccb0871305060d7b27b0554d2cc72bccf41b2705608452f315

公钥 K （x 和 y 坐标连接并作为十六进制显示）:

K = 6e### 以太坊地址格式

以太坊地址是十六进制数字，是从公钥的 Keccak-256 哈希的最后 20 个字节派生的标识符。

与比特币地址不同，所有客户端的用户界面都对后者进行了编码，以包含一个内置的校验和，以防止地址输入错误。以太坊地址以原始十六进制形式呈现，没有任何校验和。该决定的理由是，以太坊地址最终将被系统中更高层的抽象（例如名称服务）所隐藏，并且如有必要，应在更高层添加校验和。

实际上，这些更高层的开发速度太慢，并且此设计选择在生态系统的早期导致了许多问题，包括由于地址输入错误和输入验证错误而导致的资金损失。此外，由于以太坊名称服务的开发速度比最初预期的要慢，因此钱包开发者采用替代编码的速度非常慢。接下来，我们将介绍一些编码选项。

> **注意**
>
> 值得一提的是以太坊名称服务（ENS），它由 Alex Van de Sande 和 Nick Johnson 于 2017 年推出。ENS 提供了一种链上解决方案，用于将人类可读的名称（例如 `masteringethereum.eth`）转换为以太坊地址。

### 带有大小写校验和的十六进制编码 (ERC-55)

由于名称服务的部署速度缓慢，[ERC-55](https://github.com/ethereum/ercs/blob/master/ERCS/erc-55.md) 提出了一个标准。ERC-55 通过修改十六进制地址的大小写，为以太坊地址提供了一个向后兼容的校验和。其想法是，以太坊地址不区分大小写，并且所有钱包都应该接受以大写或小写字符表示的以太坊地址，而不会在解释上产生任何差异。通过修改地址中字母字符的大小写，我们可以传递一个校验和，该校验和可用于保护地址的完整性，以防止输入或阅读错误。不支持 ERC-55 校验和的钱包只是忽略地址包含混合大小写的事实，但那些支持它的钱包可以验证它，并以 99.986% 的准确率检测错误。

混合大小写的编码很微妙，您可能一开始不会注意到。我们的示例地址是：

0x001d3f1ef827552ae1114027bd3ecf1f086ba0f9

使用 ERC-55 混合大小写校验和，它变为：

0x001d3F1ef827552Ae1114027BD3ECF1f086bA0F9

您能看出区别吗？来自十六进制编码字母表的一些字母 (A–F) 现在是大写，而另一些则为小写。

ERC-55 的实现非常简单。我们获取小写十六进制地址的 Keccak-256 哈希。此哈希充当地址的数字指纹，为我们提供了一个方便的校验和。输入（地址）中的任何小更改都应导致生成的哈希（校验和）发生重大更改，从而使我们能够有效地检测错误。然后，我们的地址的哈希被编码到地址本身的大小写中。让我们逐步分解它：

1. 哈希小写地址，不带 `0x` 前缀：

Keccak256("001d3f1ef827552ae1114027bd3ecf1f086ba0f9") = 23a69c1653e4ebbb619b0b2cb8a9bad49892a8b9695d9a19d8f673ca991deae1
```

2. 如果哈希的对应十六进制数字大于或等于 0x8，则将每个字母地址字符大写。如果我们对齐地址和哈希，这会更容易显示：

   地址：001d3f1ef827552ae1114027bd3ecf1f086ba0f9
   哈希：23a69c1653e4ebbb619b0b2cb8a9bad49892a8b9...

我们的地址在第四个位置包含一个字母字符 d。哈希的第四个字符是 6，它小于 8。因此，我们将 d 保留为小写。我们地址中的下一个字母字符是 f，位于第六个位置。十六进制哈希的第六个字符是 c，它大于 8。因此，我们将地址中的 F 大写，依此类推。如您所见，我们仅使用哈希的前 20 个字节（40 个十六进制字符）作为校验和，因为我们的地址中只有 20 个字节（40 个十六进制字符）可以适当地大写。

自己检查生成的混合大小写地址，看看您是否可以说出哪些字符是大写的，以及它们对应于地址哈希中的哪些字符：

地址：001d3F1ef827552Ae1114027BD3ECF1f086bA0F9
哈希：23a69c1653e4ebbb619b0b2cb8a9bad49892a8b9...

检测 ERC-55 编码地址中的错误

现在，让我们看看 ERC-55 地址将如何帮助我们查找错误。假设我们打印出了一个以太坊地址，该地址已进行 ERC-55 编码：

0x001d3F1ef827552Ae1114027BD3ECF1f086bA0F9

现在，让我们在阅读该地址时犯一个基本错误。倒数第二个字符是大写 F。对于此示例，让我们假设我们误读为大写 E，并将以下（不正确的）地址输入到我们的钱包中：

0x001d3F1ef827552Ae1114027BD3ECF1f086bA0E9

幸运的是，我们的钱包符合 EIP-55！它注意到混合大小写并尝试验证地址。它将其转换为小写并计算校验和哈希：

Keccak256("001d3f1ef827552ae1114027bd3ecf1f086ba0e9") = 5429b5d9460122fb4b11af9cb88b7bb76d8928862e0a57d46dd18dd8e08a6927

如您所见，即使地址仅更改了一个字符（实际上，仅更改了一位，因为 e 和 f 相差一位），地址的哈希也发生了根本性的变化。这就是哈希函数的属性，使其对于校验和非常有用！

现在，让我们对齐两者并检查大小写：

001d3F1ef827552Ae1114027BD3ECF1f086bA0E9
5429b5d9460122fb4b11af9cb88b7bb76d892886...

全错了！一些字母字符的大小写不正确。请记住，大小写是正确校验和的编码。

我们输入的地址的大小写与刚刚计算的校验和不匹配，这意味着地址中已发生更改，并且已引入错误。

验证者的密码学

在本节中，我们将探讨验证者在新的基于 PoS 的共识协议中使用的密码学。虽然核心思想始终是能够对消息进行数字签名并验证它们，但有一些有趣的要求导致了与以太坊用于交易或地址的密码学不同的设计选择和最终实现。

简介

当以太坊使用 Ethash（PoW 共识算法）时，没有理由要求区块提议者（当时的矿工）对其生成的区块进行签名。事实上，基于 PoW 的共识算法不需要知道谁在创建区块才能正确工作。如果区块提议者行为不端，协议会通过让他们浪费电力和时间（即金钱）来隐式地惩罚他们。 让我们以一个矿工试图通过同时创建两个区块来进行双重支付为例。为了更好地理解这种“漏洞”背后的核心思想，假设一个矿工想买一辆车，并与经销商同意以 ETH 支付，例如 10 ETH。然后，矿工同时创建两个区块。假设它们都是有效的：在第一个区块中，矿工添加了支付交易，其中他们向汽车经销商发送了 10 ETH，而在另一个区块中，他们没有。矿工试图将链分成两部分。

根据（几乎）随机的因素，汽车经销商可能会首先收到矿工支付给他们 10 ETH 的区块。因此，汽车经销商可以假设付款进展顺利。但他们还没有把车交给矿工。事实上，汽车经销商知道在 PoW 系统中，您通常需要等待一堆区块才能认为交易已最终结算。

或多或少 12 秒后，不同的矿工在不包含 10 ETH 付款的区块之上生成了一个新区块。这是完全可能的，因为它通常取决于下一个矿工首先收到了哪个区块。现在有一条更长的区块链，并且由于 最重链规则（也（有点错误地）称为 最长链规则），该链被所有节点认为是唯一有效的链。

汽车经销商看到有效的区块链不包含他们之前收到的包含 10 ETH 付款的区块，因此他们认为付款未完成，并且他们没有把车交给矿工。

请记住，在 PoW 系统中，矿工必须花费真实的能量和时间来生成一个通过 PoW 检查的有效区块，即区块哈希低于动态阈值，因此他们花费能量和时间来创建一个区块，然后看到他们的一个区块被整个网络拒绝，这已经是一种隐式惩罚。他们浪费了宝贵的精力和时间，他们本可以更好地花在创建所有有效区块上，尊重所有规则，而不是试图作弊。

PoS 系统对于行为不端的区块生产者（即验证者）没有这种相同的隐式惩罚。相反，他们使用一种显式方法：罚没。

罚没 是通过减少（或全部）他们质押的ETH来惩罚不遵守规则的验证者的行为。 这解释了为什么验证者必须质押最低数量的 ETH 才能成为活跃验证者。 如果他们没有任何质押，如果他们开始恶意行为，协议将无法惩罚他们。

由于明确地惩罚验证者不遵守规则，因此需要确切地知道每个验证者在做什么。 为此，验证者发送的每条消息（包括区块）都必须通过其数字签名进行身份验证。

让我们重新创建之前与矿工使用的类似示例。 现在我们有一个验证者同时提出两个区块。 虽然通过 PoW，矿工应该花费双倍的能量和时间来同时生成两个有效区块，但使用 PoS 这是（几乎）完全免费的。

但这里是罚没进入场景的地方。 双重签名 - 同时提出两个区块 - 是一种可罚没的事件，因此验证者会立即受到惩罚（在这个具体示例中），即销毁他们所有质押的 ETH。

现在我们知道为什么验证者必须验证他们所有消息的身份，我们可以深入研究用于此的密码学：BLS 签名。 在下一节中，我们将看到导致最终决定使用 BLS 密码学的要求。

要求

您可以为此问题想到的第一个解决方案是 - 即需要对验证者相互发送的每条消息进行身份验证 - 是应用以太坊已经用于对每笔交易进行数字签名的相同数字签名算法：椭圆曲线数字签名算法（ECDSA）。

但它不适用于以太坊拥有的大量验证者——超过一百万。 事实上，这种数字签名算法应遵守一个基本要求：必须可以压缩签名，以减少区块中所需的空间，并减少节点验证所有验证者签名所需的时间。

现在，每个验证者都可以每 epoch 投一次票（需要进行身份验证的消息），或者 32 个 slot（我们将在第 15 章中对此进行更多扩展）。 这些消息需要通过 P2P gossip 层才能到达其他验证者和节点，并由每个其他节点进行验证以检查签名是否有效，并插入到区块中。

很容易在这里发现一个瓶颈：加入网络的验证者越多，节点需要处理的消息就越多。 即使区块变得更大，因为它们需要为那些验证者的签名保留越来越多的空间。

注意

您可以根据活跃验证者的数量轻松计算出节点需要处理的消息数量：

N = 活跃验证者的数量
1 条消息 / 1 epoch × N =
= 1 条消息 / 32 个 slot × N = ← 一个 epoch 由 32 个 slot 组成
= 1 条消息 / 32 × 12 秒 × N = ← 每个 slot 需要 12 秒
= 1 条消息 / 384 秒 × N =
= 0.0026041667 条消息 / 秒 × N

因此，我们大约每秒有 0.0026 条消息，我们需要将其与 N 相乘，N 是网络中活跃验证者的数量：

N = 1,000 → 每秒大约 2.6 条消息
N = 10,000 → 每秒大约 26 条消息
N = 100,000 → 每秒 260 条消息
N = 1,000,000 → 每秒 2,600 条消息

目前，以太坊 PoS 协议每秒处理大约 2,600 条消息。

出于这些原因，大多数 PoS 区块链的验证者集非常小，最多只有几十个或几百个。 即使是以太坊的初始提案（参见 EIP-1011）也以 900 个验证者为目标，并以 1,500 ETH 作为在活跃验证者集中当选的最低存款。

如果以太坊基金会的研究员 Justin Drake 在 2018 年 5 月的以太坊 PoS 协议的最终规范不是在 ethresearch 网站上发表的一篇长篇文章 中提出了 BLS 签名聚合的想法。

BLS 数字签名

BLS 签名以其作者的名字命名。 BLS 代表 Boneh–Lynn–Shacham，指的是三位密码学家 Dan Boneh、Ben Lynn 和 Hovav Shacham，他们在 2001 年的论文 "来自 Weil 配对的短签名" 中介绍了签名方案。

与 ECDSA（将在第 6 章中进一步解释）一样，BLS 签名仍然基于椭圆曲线密码学。 特别是，以太坊使用曲线 BLS12-381，这是 Sean Bowe 在 2017 年为 Zcash 协议工作时设计的。 它由以下函数定义：

y^2 = x^3 + 4

在整数模 q 上，其中 q 是一个 115 位十进制数字的数字：0x1a0111ea397fe69a4b1ba7b6434bacd764774b84f38512bf6730d2a0f6b0f6241eabfffeb153ffffb9feffffffffaaab。

它是如何工作的？

核心思想与 ECDSA 的工作方式非常相似：有一个秘密密钥，从中派生出一个公钥。 然后，每条消息都使用秘密密钥进行签名，其他所有人都可以通过使用相应的公钥来验证其完整性。

秘密密钥 (sk) 是 1 到 r – 1 之间的整数，其中 r 是这个巨大的数字：0x73eda753299d7d483339d80809a1d80553bda402fffe5bfeffffffff00000001。 它有 77 位十进制数字！

公钥 (pk) 通过执行 sk * g1 获得，这是椭圆曲线点的标量乘法，其中 g1 是一个名为 G1 的群的生成器。 pk 以压缩和序列化的格式表示，从而产生一个 48 字节的字符串。

签名的消息 (m) 始终映射到椭圆曲线点，该点是称为 G2 的不同群的成员。 您可以将此映射视为一种哈希函数，该函数接受消息 m - 即实际的验证者证明 - 并输出 G2 中的一个点 H(m)，以其压缩序列化形式表示为一个 96 字节的字符串。

最后，我们通过执行 sk * H(m)（G2 中的新椭圆点）来获得消息 m 的签名 (σ)。

ECDSA 和 BLS 之间的关键区别在于这两个协议的底层细节——即，它们用于验证签名正确性的数学技术。 事实上，虽然 ECDSA 涉及数学线性计算，例如椭圆曲线上的标量乘法和加法，但 BLS 签名依赖于 椭圆曲线双线性配对 的更复杂的算术。

事实上，签名 σ 只有在以下等式成立时才有效：

e(g1,σ) = e(pk, H(m))

其中 e 是椭圆曲线双线性配对。

椭圆曲线属性内部

完全理解前面的等式需要深入了解椭圆曲线、配对和所有那些巨大的兔子洞。 但是，理解它的一个简单方法是简单地遵循此处的步骤。 您不会掌握配对具有该属性的原因和方式的所有细节，但它仍然可以帮助您熟悉它：

e(pk, H(m)) = e(sk * g1,H(m)) = ← pk = sk * g1
= e(g1, H(m))^sk = ← 感谢配对属性
= e(g1, sk * H(m)) = ← 感谢相同的属性
= e(g1,σ) ← σ = sk * H(m)

正如 Vitalik Buterin 在 Medium 文章 中指出的那样：

如果您将椭圆曲线点视为单向加密的数字 - encrypt(p) = p * G = P，其中 G 是生成器点 - 那么，传统的椭圆曲线数学让您可以检查数字的线性约束（例如，如果 P = G * p、Q = G * q 和 R = G * r，检查 5 * P + 7 * Q = 11 * R 实际上是在检查 5 * p + 7 * q = 11 * r），配对让您可以检查二次约束（例如，检查 e(P, Q) * e(G, G * 5) = 1 实际上是在检查 p * q + 1 * 5 = 0）。

您可以想象，更复杂的算术也意味着需要更多时间来生成和验证签名。 以太坊仅将 BLS 签名用于验证者的唯一原因是它们极其重要的 签名聚合 属性。

事实上，如果您将两个 ECDSA 签名加在一起，您不会获得有意义的结果。 如果您尝试使用该结果来证明初始签名消息的完整性，您将无法通过任何测试。

相反，如果您将两个 BLS 签名加在一起，您只是在做椭圆曲线加法。 结果是 G2 中的一个新椭圆曲线点，您可以针对两个对应的公钥的总和（它仍然是 G1 中的一个椭圆曲线点）使用它来正确验证初始签名消息的完整性。

注意

聚合签名和聚合公钥与单个签名和单个公钥无法区分，因此您可以使用完全相同的算法来验证聚合签名的正确性。

聚合签名和公钥：

σagg = σ1 + σ2 + σ3 + … + σn
pkagg = pk1 + pk2 + pk3 + … + pkn

聚合签名验证：

e(pkagg,H(m)) =
= e(pk1 + pk2 + pk3 + ... + pkn,H(M)) =
= e((sk1 + sk2 + sk3 + ... + skn) * g1,H(m)) =
= e(g1,H(m))^(sk1 + sk2 + sk3 + ... + skn) =
= e(g1,(sk1 + sk2 + sk3 + ... + skn) * H(m)) =
= e(g1,σ1 + σ2 + σ3 + ... + σn) =
= e(g1,σagg)

总结

密码学非常困难。它需要深入的数学背景。本书实际上不是为密码学家编写的，因此总结我们在前几节中简要介绍的内容至关重要。我们解释了 BLS 签名如何工作，以及为什么选择它作为验证者在新 PoS 共识协议中使用的数字签名算法：它们的聚合属性使您可以将更多数字签名压缩为一个，从而减少了存储它们所需的空间和验证它们的时间，而不会损失任何安全性。

现在我们可以做一个快速示例来演示验证者如何在“现实生活中”使用 BLS 算法，以及签名聚合如何发挥作用。图 4-6 说明了一个场景，其中我们有三个验证者想要表达他们对区块 A 的投票。因此，他们投下他们的票，对其进行签名，并相互分享。

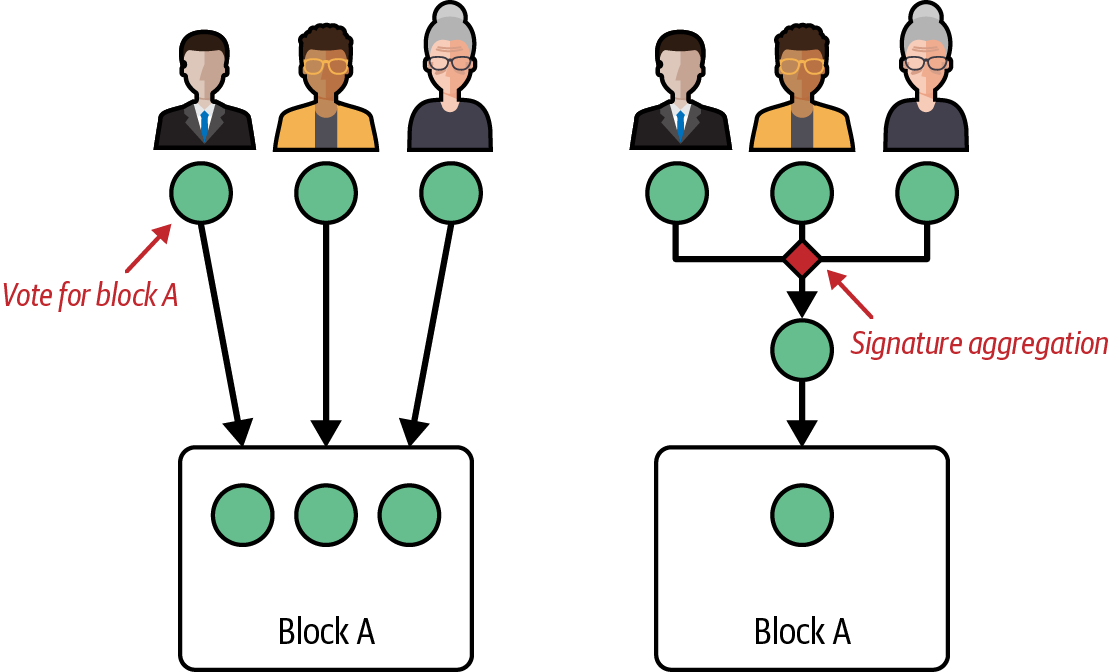
图 4-6。 BLS 签名聚合：三个验证者投票和签名

如果没有 BLS，您需要将所有三个已签名的投票保存到区块中以永久存储它们。 有了 BLS，您可以将所有三个已签名的投票聚合到一个新的聚合投票中，并且仅将该投票存储到区块中。

这不仅节省了空间，而且还大大减少了所有以太坊节点在验证有已签名投票时必须执行的时间和计算量，因为它们可以直接验证聚合投票，而不是对每个单独的已签名投票执行验证。 BLS 密码学的神奇之处在于，聚合结果与普通签名没有区别：这意味着验证聚合签名的有效性并不比验证单个签名的有效性更难。 因此，通过显着减少要验证的已签名投票的数量，但需要相同的计算量来验证每个已签名投票，完整节点必须执行的总计算量（因此，时间）比不使用 BLS 聚合签名的情况要低得多，如图 4-7 所示。

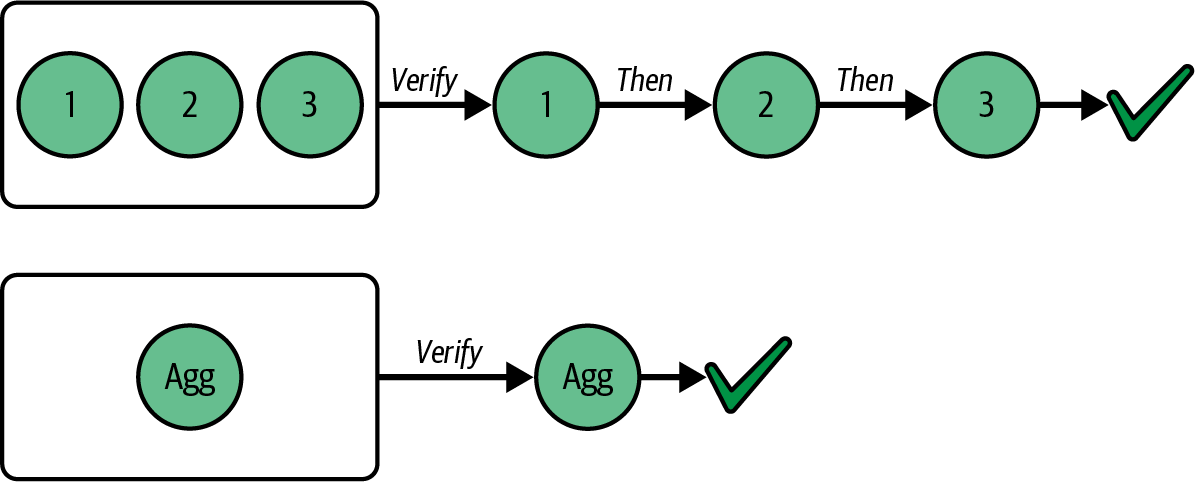
图 4-7。 BLS 签名聚合减少了验证时间

如果验证者不遵守规则怎么办？ 如果验证者恶意行为——例如，通过双重签名，或同时投票给两个不同的区块——协议可以检测到这种行为并相应地惩罚验证者，如图 4-8 所示。

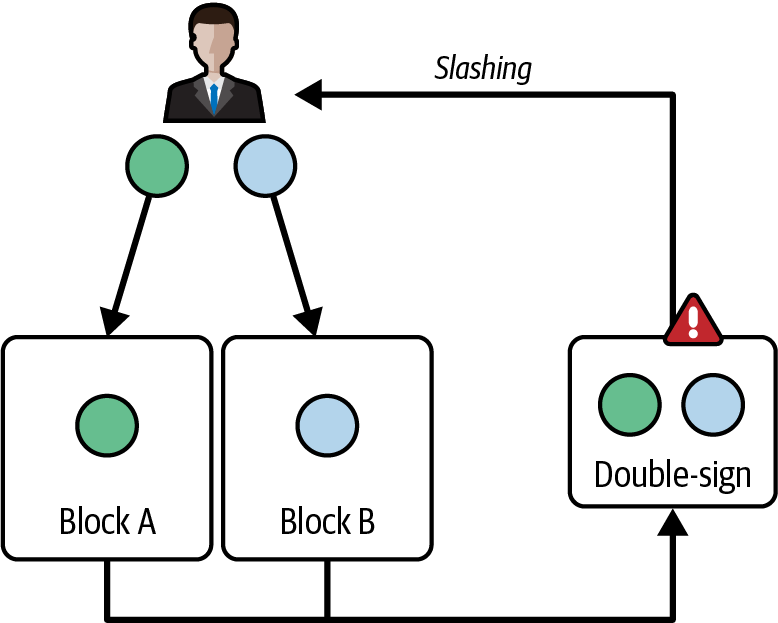
图 4-8。 BLS 签名支持检测恶意验证者

事实上，由于所有投票都使用 BLS 签名方案进行数字签名，因此很容易识别负责不当行为的验证者，并相应地罚没他们。

KZG 密码学

2024 年 3 月 13 日，以太坊升级到 Cancun-Deneb (Dencun) 硬分叉。 此升级包含许多更改，但最重要的是引入了一种新型交易：EIP-4844 blob 交易。

我们不会在这里深入探讨 blob 交易对以太坊路线图的重要性，因为我们将在第 16 章中更详细地介绍。 相反，在接下来的部分中，我们将探索这种新型交易背后的密码学：多项式承诺方案，更具体地说是 KZG 承诺方案。

简介

在研究多项式承诺方案之前，重要的是要了解我们面临的问题以及我们想要达到的最终目标。

注意

在本节中，我们将简要提及第 2 层（L2）。 虽然 L2 将在第 16 章中得到适当的解释和扩展，但至少对其进行快速介绍可能会有所帮助。 L2 是以太坊的一种新的扩展解决方案：它们是真实的区块链，具有独特的历史和状态，定期将其所有更新和数据发布到以太坊主网。 理由是，必须能够仅通过查看以太坊主网来推导出整个 L2 区块链。

不深入讨论细节，L2 每天都会将大量数据发布到以太坊主链中。 所有这些数据都必须由网络中的所有节点下载和验证。 这种情况通常会导致 gas 费用飙升，在紧急情况下，仅进行一次 ETH 转账的费用就可能达到 10-20 美元。

最终，我们不想直接将所有这些数据发布到链上，而只想存储对其的承诺——即加密哈希——将所有数据留在以太坊链之外。 但是，仅发布哈希会产生一个新问题：网络中的所有节点必须确保承诺指向的数据存在于某个地方。否则，我们可能会丢失关键数据。

第一个（显而易见的）解决方案是强制所有节点临时下载完整数据，以便它们可以轻松地验证承诺是否有效——即，它指向它们拥有的完整数据。 这就是我们在编写本章时的状态（2025 年 6 月）。

长期的解决方案是不要求所有节点下载完整数据，而只下载其中的一小部分。 然后，节点可以使用加密证明，以确保数据完全可用。 这些证明必须很小，并且需要快速验证。 我们的想法是，证明（和验证）数据可用比下载数据并直接验证它要快得多也更轻量级。 此策略称为 数据可用性采样 (DAS)，是以太坊社区中最重要的研究领域之一。

为了实现 DAS 的最终目标，我们想要一个加密系统，使我们（所有节点）能够：

• 创建对一些数据的承诺（您想要证明其存在且完整可用的数据）
• 为与先前创建的承诺相关的数据生成小证明
• 轻松验证这些证明

此加密系统可以选择性地（但在理想情况下）不泄露太多关于它所引用数据的信息。

在下一节中，我们将探索这样一种加密系统：多项式承诺方案，更具体地说是 KZG 承诺方案。

注意

您可能想知道为什么我们讨论的是多项式承诺方案，而不是数据承诺方案。 这是一个非常好的问题：我们的目标是能够承诺一些数据，而不是多项式。 但这里有个诀窍：数据可以用多项式表示。 因此，如果我们能够生成多项式承诺方案，那么我们就没问题了。

多项式承诺方案

多项式承诺方案 允许证明者计算对多项式的承诺，其属性是可以（在以后）在任何位置对该承诺进行“打开”——求值。 证明者可以证明多项式在某个位置的值等于声明值，并且可以为该声明生成证明。 验证者既有承诺又有证明，可以验证证明是否有效，当且仅当证明者没有作弊——即，承诺的多项式实际上在选定位置求值为声明值时。

多项式简介

我们将在本节中大量讨论多项式，因此重要的是确保每个人都知道什么是多项式，因为您可能已经很久没有在学校学习它们了。

多项式是这样的数学表达式：

x^3 + 3x^2 – 9

其中 x 是变量，所有数字（1、3、0、–9）都是系数。 请注意，我们将 0 作为第三个系数，因为该多项式实际上是以下多项式：

x^3 + 3x^2 + 0x – 9

在本节中，我们将多项式称为 p(x)：

p(x) = x^3 + 3x^2 + 0x – 9

我们还需要多项式的 度 n。 它是多项式中最高次幂的数字。 我们的多项式示例的度为 3。 所以 n = 3。

描述多项式的通用公式如下：

p(x) = p₀ + p₁x + p₂x² + ... + pₙxⁿ

或更正式地说：

p(x) = Σ pᵢxⁱ (对于 i = 0 到 n)

其中 n 是多项式的度，pi 是其所有系数。

使用 Merkle 树

让我们开始研究使用经典 Merkle 树数据结构的多项式承诺方案。 如果您有兴趣深入研究 Merkle 树，我们将在第 14 章中对其进行扩展。

我们可以通过将树的所有叶子元素设置为等于我们要承诺的多项式的所有系数 pi，来承诺度为 n = 2^d – 1 的多项式，其中 d 是 Merkle 树的深度。

请看以下示例：

p(x) = x^7 + 5x^5 – 2x^4 + 3
n = 7 ← p(x) 的度
d = 3 ← 所需 Merkle 树的深度

图 4-9 显示了应用于此示例的多项式承诺方案，该方案使用 Merkle 根作为核心密码学原语。

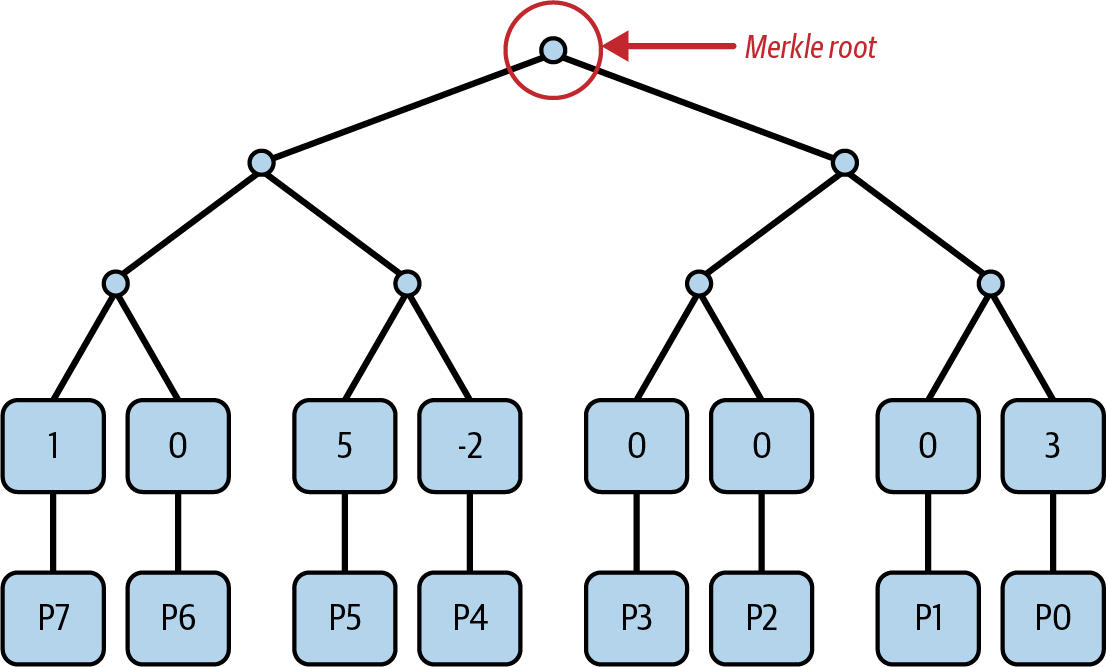
图 4-9。 使用 Merkle 树的多项式承诺

最终承诺是我们通过构建完整 Merkle 树获得的 Merkle 根。 现在假设我们想要（向验证者）证明 p(1) = 7。 此语句为真，因为如果您采用 p(x) 并设置 x = 1，您可以轻松地计算出该位置的多项式求值为 7。

为了证明我们断言 p(1) = 7，我们需要发送给验证者：

• 我们想要证明的语句：p(1) = 7
• Merkle 根——即对多项式 p(x) 的承诺
• 多项式的所有系数 pi

这样，验证者可以获取所有系数 pi，并在 x = 1 时计算多项式的值。 在这里，验证者验证我们的断言实际上是真的。 然后，验证者获取所有系数 pi 并计算 Merkle 树，将其 Merkle 根与我们提供给它们的 Merkle 根进行比较。 在这里，它们验证我们最初承诺的多项式实际上与我们发送给它们的多项式相同。

为了回顾使用 Merkle 树的多项式承诺的属性，我们有以下内容：

承诺大小

承诺是 Merkle 根，它是一个单一哈希，通常长 32 字节。

证明大小

为了证明一个评估，我们需要发送多项式的所有系数 pi。 这意味着证明大小在多项式度 n 中是线性的。

验证者复杂度

验证者必须做线性工作（在多项式的度中）才能完全验证我们的断言。 事实上，验证者拥有所有系数 pi，并且必须计算 Merkle 树和多项式在声明点的评估。

方案隐私

由于证明者发送多项式的所有系数 pi，因此该方案不会隐藏关于多项式的任何信息。

这些属性并不理想，因为多项式的度 n 在实际以太坊协议中可能非常大，并且在网络上发送其所有系数所需的带宽太高。 此外，我们希望有一种协议可以让证明者尽可能少地泄露关于承诺多项式的信息。

幸运的是，有一种方案可以满足我们的所有要求，这就是 KZG 进入场景的地方。

KZG 承诺

KZG 是 Kate、Zaverucha 和 Goldberg 这三个作者姓名的首字母缩写。 这些密码学家在他们 2010 年的论文 "多项式的恒定大小承诺及其应用" 中介绍了这种承诺方案。

受信任的设置

KZG 承诺方案需要存在 受信任的设置。 您可以将其视为与密码学协议的所有参与者（即证明者和验证者）共享的通用知识库。 它被称为受信任的设置，因为为了生成该通用知识库，一些参与者需要生成随机数（秘密），加密它们并创建最终数据。 然后，他们必须删除秘密以确保协议保持安全。 由于需要信任这些参与者删除他们的秘密，因此整个仪式被称为受信任的设置。

现代设置通常使用 Powers-of-Tau 设置，该设置具有 1-of-N 信任模型。 这意味着我们只需要一个诚实的参与者才能使整个受信任的设置被认为是安全的。

以太坊 KZG 受信任的设置仪式涉及超过 140,000 个不同的参与者，如图 4-10 所示。

图 4-10。 以太坊 KZG 受信任的设置仪式的参与者

更具体地说，受信任的设置生成 [s^i]₁ 和 [s^i]₂ 元素，其中 i = 0, 1, … , n – 1，其中：

• s 是受信任的设置秘密，无人知晓（由每个参与者生成的秘密总和构成）
• [s^i]₁ 和 [s^i]₂ 实际上是椭圆曲线点（分别位于曲线 G1 和 G2 中）
• n 是多项式的阶数

提示

当您看到方括号内的内容时，它表示一个椭圆曲线点。

承诺

如您所见，KZG 承诺方案（再次）涉及椭圆曲线和配对，这是我们已经在 BLS 数字签名中看到的。

请记住，在椭圆曲线上，如果您有一个秘密数字 a，您可以通过椭圆曲线乘法获得一个椭圆曲线点 [a]：

[a]₁ = aG₁

并且计算上不可能返回。 因此，如果您只有 [a]，您就无法获得秘密 a。

即使证明者和验证者都不知道 s（受信任的设置秘密），他们仍然可以对其执行某些操作：

c[s^i]₁ = cs^iG₁ = [cs^i]₁ ← 椭圆曲线乘法； c 是一个整数
c[s^i]₁ + d[s^i]₁ = (cs^i + ds^i)G₁ = [cs^i + ds^i]₁ ← 椭圆曲线点的加法

因此，如果 p(x) = p₀ + p₁x + p₂x² + ... + pₙxⁿ 是一个多项式，证明者可以计算：

[p(s)]₁ = [p₀ + p₁s₁ + p₂s²₁ + ... + pₙsⁿ₁] = p₀ + p₁[s]₁ + p₂[s²]₁ + ... + pₙ[sⁿ]₁

由于 [s^i]₁ 是受信任的设置的一部分，因此它是常识，证明者能够在无人知晓的秘密点 s 评估多项式。 听起来很神奇，对吧？ 但要注意一件事：前一个操作的输出不是整数；相反，它是椭圆曲线点。 [p(s)]₁ 椭圆曲线点是我们对多项式 p(x) 的 KZG 承诺。

KZG 的可靠性：为什么证明者不能伪造证明者是否能在不知道秘密 s 的情况下，找到一个不同的多项式 q(x) != p(x)，使得它们具有相同的 KZG 承诺：[q(s)]₁ = [p(s)]₁？如果可以，证明者将能够让验证者认为他们知道一个多项式 p，即使这不是真的。

假设他们可以，那么存在一个 n 阶非常数多项式 r(x) = p(x) – q(x)。由于 q(x) != p(x)，这意味着 r(x) 最多有 n 个零点 —— 即，在最多 n 个位置上 r(x) = 0。 这是代数的一个基本性质。你可以很容易地验证，对于你在学校学过的所有基本几何形状，这个性质都成立：直线（1 阶多项式）有一个零点，抛物线（2 阶多项式）最多有两个，以此类推。

证明者实现 q(s) = p(s) 的唯一方法是使 r(x) = p(x) + q(x) = 0 在尽可能多的地方成立。但正如我们之前所说，他们最多可以选择 n 个零点。

由于证明者不知道 s，他们极不可能猜到它。实际上，n（多项式的阶数）<< p（椭圆曲线的阶数）。

如果 n = 228 且 p = 2^256，则 s 是所选零点之一的概率为 2 × 10^-69。

因此，我们可以说，虽然存在许多具有相同承诺 C = [p(s)]₁ 的多项式，但它们是不可能计算出来的。这是一种计算绑定。

到目前为止，我们能够通过在秘密点 s 处评估多项式 p(x) 来对它进行承诺，但我们仍然缺少一种方法来证明最初证明者的断言 p(z) = y 是真实的，而无需将所有系数 pi 发送给验证者。在这里，椭圆曲线配对再次派上用场。

KZG 证明

为了理解最终的 KZG 证明，我们需要回顾多项式的一些重要属性。

如果多项式 p(x) 在 z 处有一个零点，那么它可以被 (x – z) 整除。这很容易理解。取多项式 p(x) = x² – 4，它也可以表示为 p(x) = (x + 2)(x – 2)。由于 p(2) = 4 – 4 = 0，因此 p(x) 可以被 (x – 2) 整除。

反之亦然。如果 p(x) 能被 (x – z) 整除，那么它在 z 处有一个零点。取我们之前用过的同一个例子，你可以很容易地证明这一点。

记住，我们（作为证明者）想要证明 p(z) = y。在这一点上，我们取多项式 p(x) – y。这个多项式在 x = z 处的值为零，因此我们可以使用前面描述的属性 —— 特别是，由于 p(x) – y 在 z 处有一个零点，那么它可以被 (x – z) 整除。

因此，我们可以计算商多项式 q(x)：

q(x) = [p(x) – y] / (x – z)

我们可以将其写成等价形式：

q(x)(x – z) = p(x) – y

注意

这里需要非常注意的是，商多项式 q(x) 只有在 p(x) – y 可以被 x – z 整除时才能计算出来。否则，这将是不可能的，因为我们总是会有一个余数。

为了更好地理解这一点，让我们看一个例子。再次取多项式 p(x) = (x + 2)(x – 2)。由于这个多项式可以被 (x + 2) 整除，我们可以计算商多项式：

q(x) = p(x) / (x + 2) = [(x + 2)(x – 2)] / (x + 2) = x – 2

如果我们尝试除以 (x – 3)，我们将无法获得商多项式。如果你愿意，可以使用之前的例子来尝试...

现在我们已完全准备好生成我们的证明。实际上，断言 p(z) = y 的 KZG 证明是 π = [q(s)]₁。 基本上，它是（椭圆曲线点）商多项式在秘密点 s 处的值。

验证者通过计算以下等式来检查此证明的有效性：

e(π, [s – z]₂) = e(C – [y]₁, H)

其中：

• π = [q(s)]₁ 是 KZG 证明
• C = [p(s)]₁ 是多项式 p(x) 的承诺
• H 是 G2 群的生成器，证明者和验证者都知道

让我们证明这个密码方案同时具有以下两个特点：

正确性

如果证明者遵循所有规则，那么他们必须能够产生一个有效的证明，验证者应该能够正确地验证。

可靠性

证明者不能通过计算伪造证明来欺骗验证者 —— 也就是说，证明者不能让验证者相信对于某些 y′ != y，p(z) = y′ 成立。

正确性

如果我们取验证者等式并将其写入配对群，基本上计算配对操作，我们得到：

[q(s)(s – z)]ₜ = [p(s) – y]ₜ

其中 T 是不同的椭圆曲线。

你可以看到这个等式与我们之前计算的完全相同：

q(x)(x – z) = p(x) – y

在秘密点 s 处计算。唯一的区别是，我们有椭圆曲线点而不是数字。

通过构造，该等式始终成立。这就是正确性部分。

可靠性

证明者能伪造吗？ 这意味着：即使 p(z) = y′ 并不成立，证明者是否可以声明 p(z) = y′ 并且仍然通过验证者检查？

为了尝试这样做，验证者有两个选择：

1. 验证者可以尝试遵循正常程序，只需更改声明的值 y′。因此，他们必须通过将 p(x) – y′ 除以 (x – z) 来计算商多项式。但这是不可能的，因为 p(z) – y′ != 0 —— 这里无法进行多项式除法。 你可能想知道：如果证明者能够选择一个 y′ != y，使得 p(x) – y′ = 0 呢？ 实际上，我们已经在之前的注释中给出了答案，即概率接近于零。 证明者无法计算出这样的 y′。 第一种解决方案不是一个具体的选择。

2. 验证者可以在构建证明时直接在椭圆曲线上工作。 实际上，如果他们能够生成证明：

   π′ = [C – y′] / [s – z]₂

   那么他们可以证明任何他们想证明的东西：

   e(π′, [s – z]₂) = e(C – [y′]₁, H) →
   → e(π′, [s – z]₂) = e(C – [y′]₁, H) →
   → (C - y`)/(s - z)*(s - z) = C - y` →
   → C - y` = C - y`  ← 这总是真的。

   但同样，对于证明者来说，计算这个证明在计算上是不可能的，因为它需要知道 s，而 s 是可信设置的秘密，没有人知道它的值。

KZG 属性

为了回顾使用 KZG 证明系统进行多项式承诺的属性，我们有：

承诺大小

承诺是允许配对的椭圆曲线的单个群元素 —— 例如，对于曲线 BLS12_381，其压缩形式为 48 字节长。

证明大小

证明大小独立于我们承诺的多项式 p(x) 的大小。 它始终是椭圆曲线的一个群元素。

验证者复杂度

验证也独立于多项式的大小，只需要两个（椭圆曲线）群乘法和两个配对。

方案隐私

该方案能够最大程度地隐藏证明者承诺的多项式 p(x)。 实际上，虽然使用 Merkle 树时证明者必须发送所有系数，但使用 KZG 时他们只需要发送在秘密点 s 处计算的商多项式，即使它是一个椭圆曲线点而不是一个整数。

多重证明

我们能够证明多项式 p(x) 的单个计算结果，但我们可以做更多的事情。 我们可以证明多项式在任何数量的点上的计算结果，并同时使用相同的证明大小。

让我们看看这是如何工作的。 我们想证明对于每个 zᵢ，p(x) 的计算结果为 yᵢ：

(z₀, y₀), (z₁, y₁), …, (zₖ₋₁, yₖ₋₁)

我们总是可以找到一个阶数低于 k 的多项式，它通过所有这些点。 这是一个代数性质，并且还有一个生成该多项式的数学公式，称为插值多项式 I(x)：

I(x) = Σ yᵢ · ∏ (x – zⱼ)/(zᵢ – zⱼ)  (对于 i,j = 0 到 k-1，j ≠ i)

虽然这听起来很困难，但实际上很容易掌握。 假设我们有两个不同的点，如图 4-11 所示：

A = (1, 0)
B = (2, 1)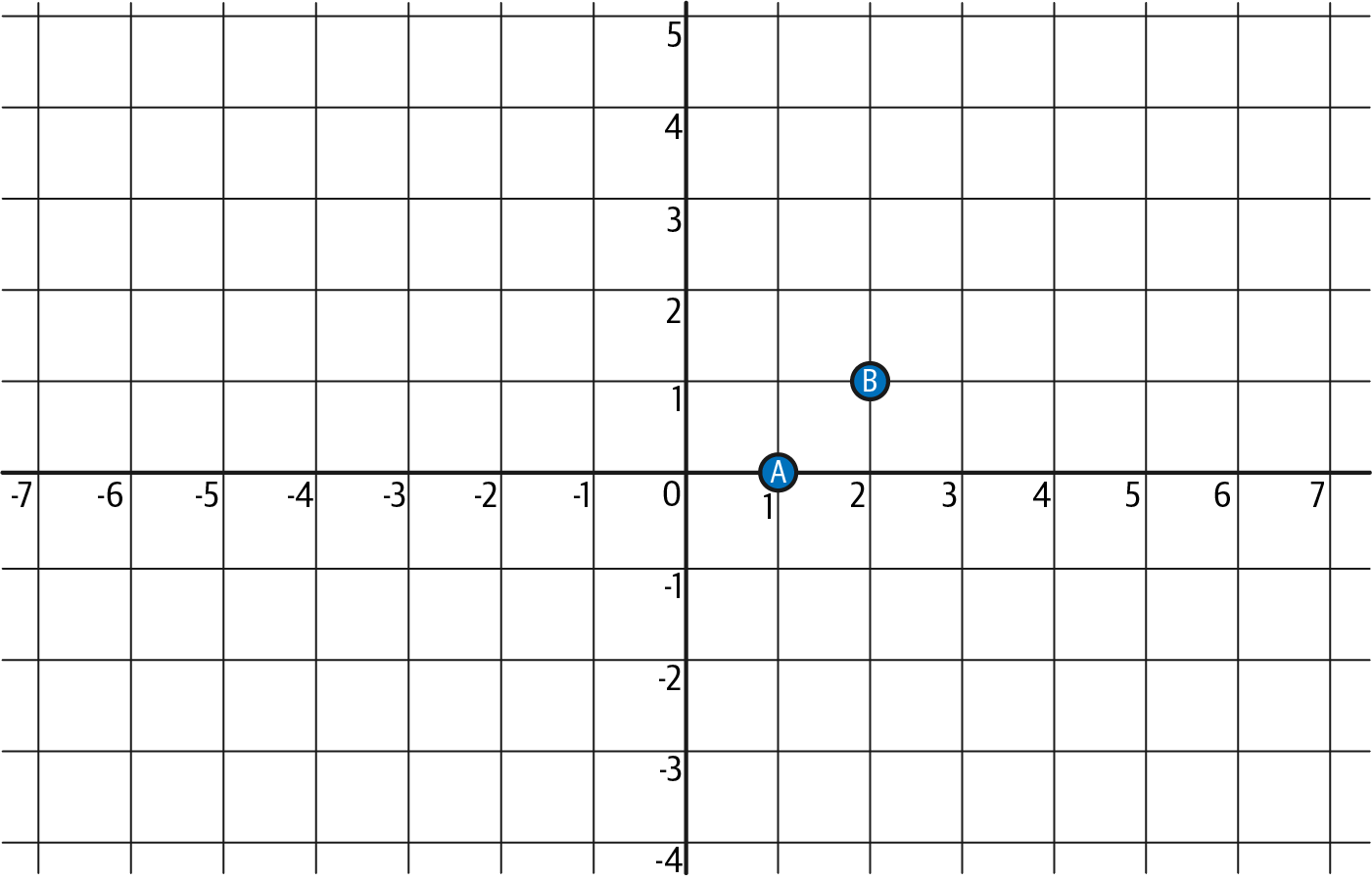

图 4-11。 两个不同的点 A 和 B

很容易理解，有一条线 —— 一个 1 阶多项式（小于点数 2）—— 通过 A 和 B。

那条线是：

I(x) = x – 1

图 4-12 更好地说明了这一点。

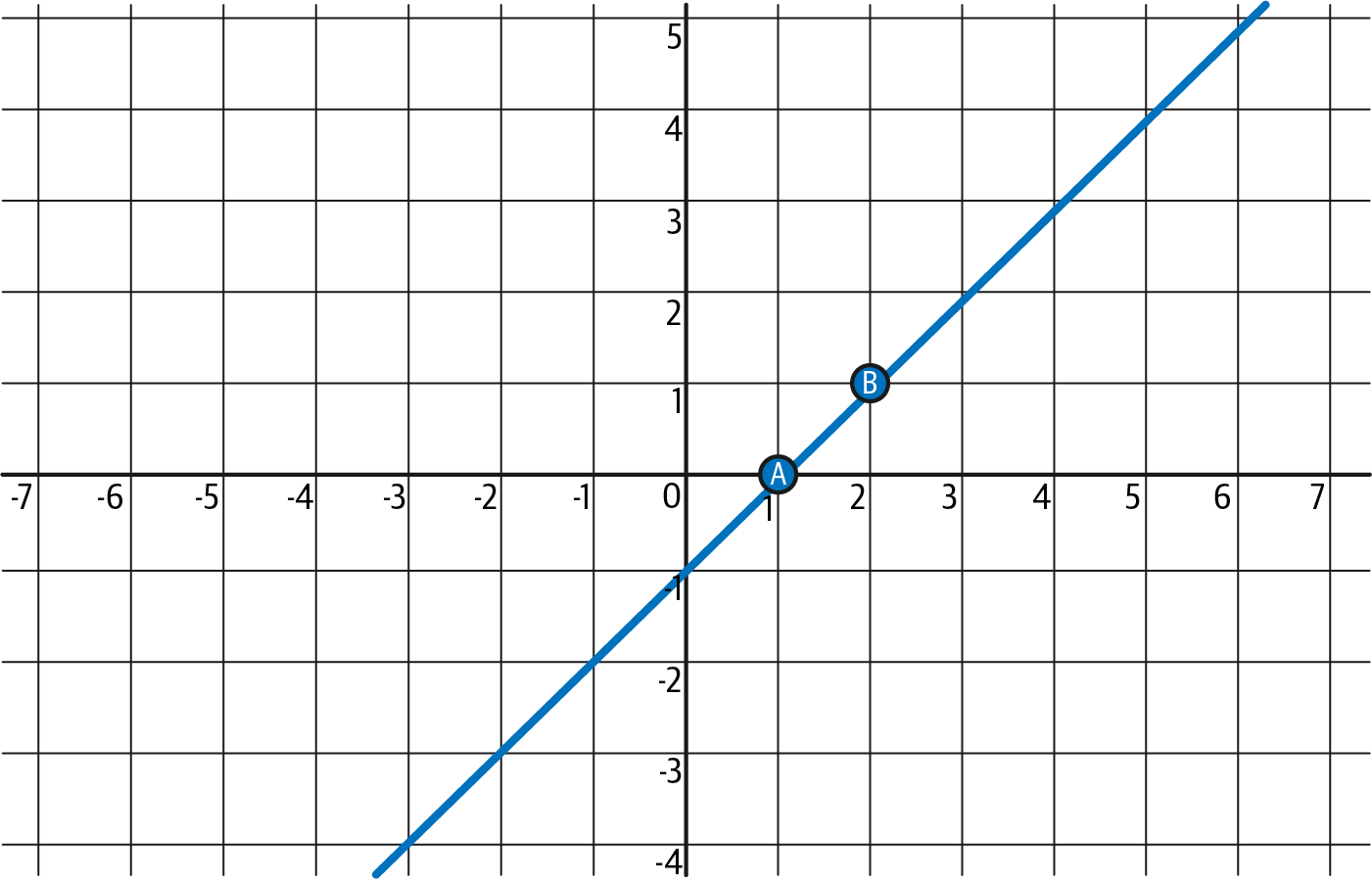
图 4-12。 穿过点 A 和 B 的插值多项式（线）

在这里，我们使用了我们的直觉，但我们可以使用该公式来证明结果是相同的。 记住我们有 k = 2：

I(x) = y₀ · (x – z₁)/(z₀ – z₁) + y₁ · (x – z₀)/(z₁ – z₀)
     = 0 · (x – 2)/(1 – 2) + 1 · (x – 1)/(2 – 1)
     = 0 + (x – 1) = x – 1

由于证明者想要证明 p(x) 通过本节开头提到的所有点，并且我们假设这是真的 —— 也就是说，证明者是值得信赖的 —— p(x) – I(x) 在每个 z₀, z₁, …, zₖ₋₁ 点处都为零。

这意味着它可以被 (x – z₀)(x – z₁)...(x – zₖ₋₁) 整除。 我们称这个多项式 Z(x) 为 零化器。

现在，我们继续使用通常的方法。 证明者计算商多项式 q(x)：

q(x) = [p(x) – I(x)] / Z(x)

并生成证明 π = [q(s)]₁。 请注意，此证明是通常的（单个椭圆曲线点）KZG 证明。

为了检查此证明的有效性，验证者需要：

1. 通过应用先前描述的公式来计算 I(x)，然后计算 [I(s)]₁。
2. 计算 Z(x)，然后计算 [Z(s)]₂。 请注意，验证者可以计算 Z(x)，因为他们知道证明者想要证明的所有声明的点（和值）。
3. 然后应用通常的等价性检查：

e(π, [Z(s)]₂) = e(C – [I(s)]₁, H)

通过在配对群中写入该方程式：

q(s)Z(s) = p(s) – I(s)

这与证明者之前计算商多项式时的等式相同，唯一的区别是这里是在秘密点 s 处进行计算。

总结

让我们总结一下 KZG 承诺方案中完整的证明者↔验证者流程。

我们从证明者开始，他掌握一些数据。 他们立即将这些数据编码为多项式，如图 4-13 所示。

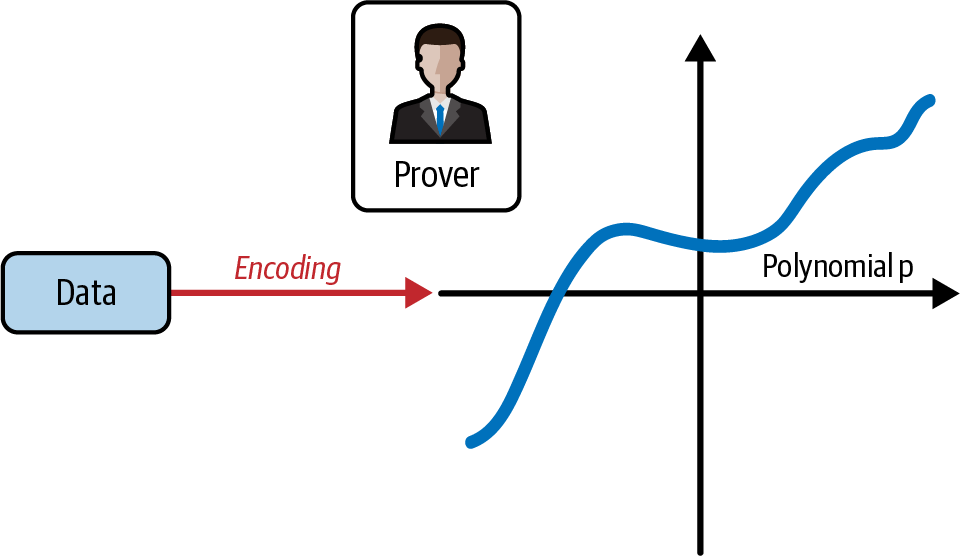
图 4-13。 证明者将数据编码为多项式 p

证明者的目标是让验证者相信他们知道某个数据，现在已编码为多项式。 但是，证明者不想透露整个数据集。 相反，他们希望验证者能够验证有关数据的特定声明。 特别是，证明者希望验证者确认多项式在特定点处评估为预期值，如图 4-14 所示。

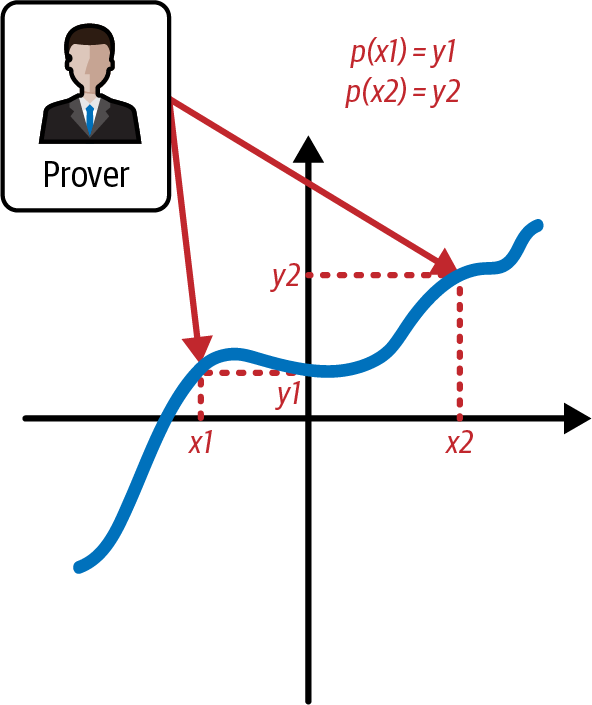
图 4-14。 证明者想要证明多项式在特定点的计算结果

为了实现此目标，证明者计算多项式的 KZG 承诺并将其发送给验证者，如图 4-15 所示。

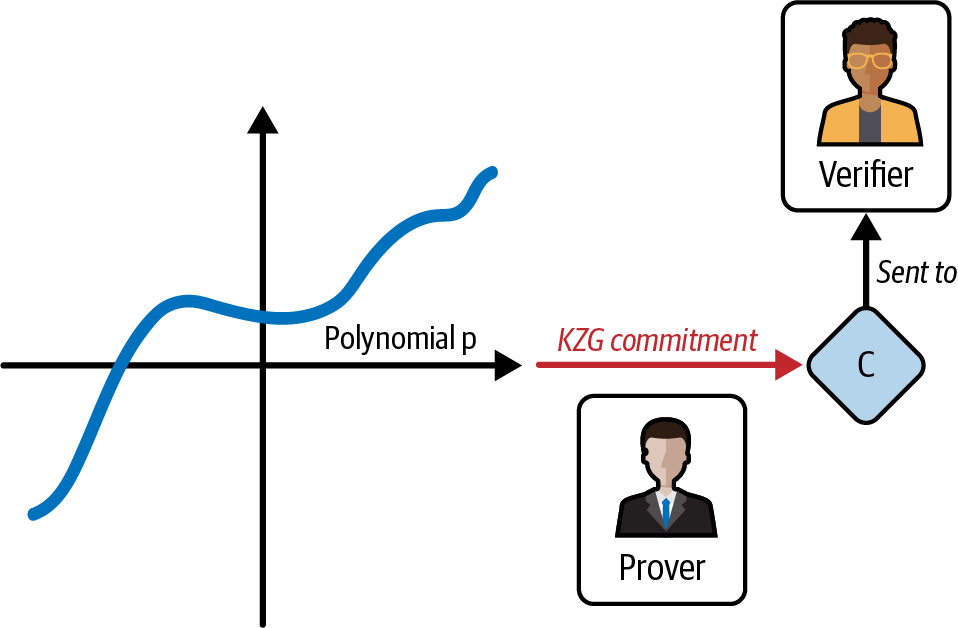
图 4-15。 证明者计算 KZG 承诺 C 并将其发送给验证者

然后，证明者需要计算他们想要向验证者证明的所有计算结果的 KZG 证明，如图 4-16 所示。

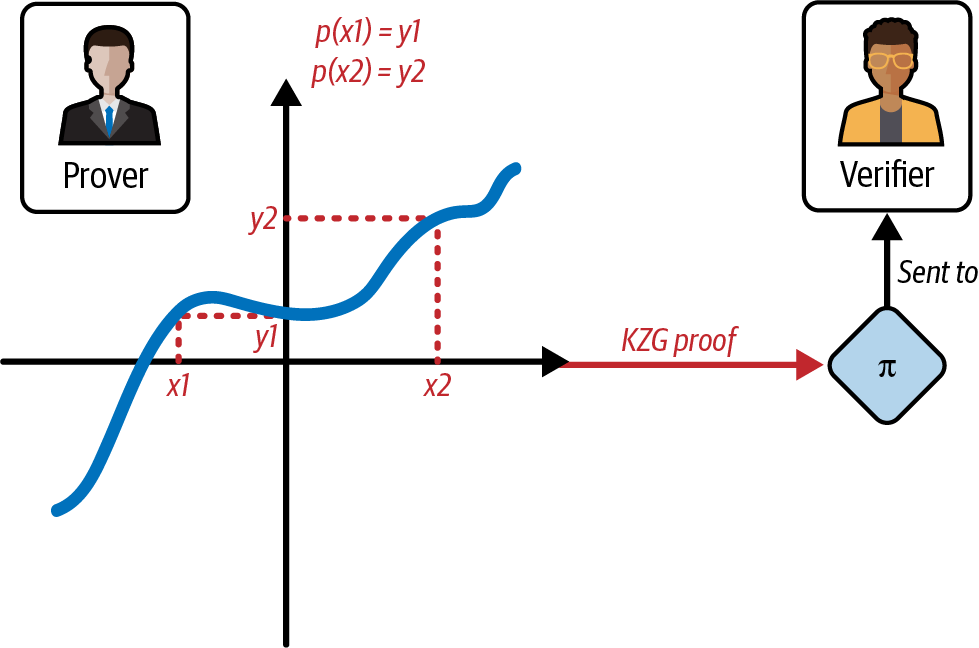
图 4-16。 证明者计算多项式不同评估 的KZG 证明并将其发送给验证者

现在，轮到验证者了。 为了确保证明者是诚实的，验证者需要使用证明者先前发送的信息以及可信设置来计算椭圆曲线配对检查，如图 4-17 所示。

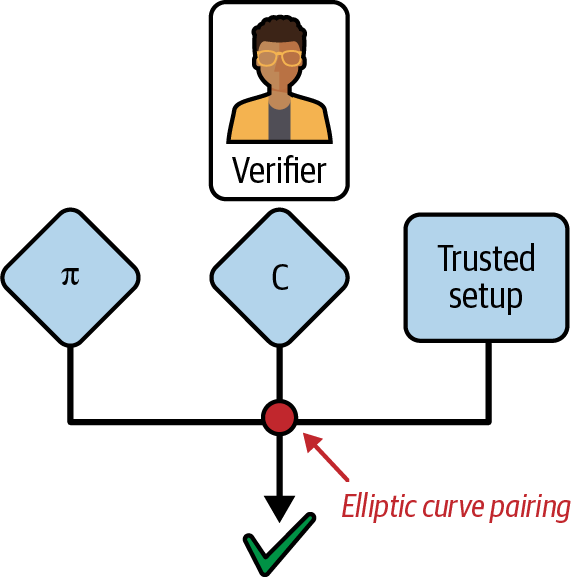
图 4-17。 验证者通过椭圆曲线配对运算检查评估的有效性

结论

我们提供了 PKC 的概述，并重点介绍了公钥和私钥在以太坊中的使用，以及密码工具（例如哈希函数）在创建和验证以太坊地址中的使用。 我们还研究了数字签名以及它们如何在不泄露密钥的情况下显示私钥的所有权的方式。 在第 5 章中，我们将把这些想法结合在一起，并研究如何使用钱包来管理密钥集合。