你的AI智能体会被迫耗尽钱包吗？DeFi中AI的结构性风险

当一个 Transformer 控制着一个价值 1 亿美元的 DeFi 金库时，它会被“越狱”并耗尽资金吗？当一个 AI 预言机在链上发布“匿名化”的嵌入（embeddings）时，攻击者可以恢复私人数据吗？这些不是假设性问题，而是由最近关于深度神经网络和 AI 模型的功能属性的两条定理所施加的架构约束。

这个分为两部分的文章系列解释了为什么这些属性对于 AI 驱动的加密协议很重要，以及如何在即使存在这些属性的情况下仍然构建安全的系统。第一部分建立了数学基础。第二部分（即将推出）提供了具体的机制、攻击场景和防御措施。

概述

一个现代的 Transformer 是一个函数 $$ f_\theta: \mathcal{X} \to \mathcal{Y} $$ 由 $\theta$ 参数化，通常使用随机梯度下降进行训练。多年来，我们从统计学角度分析这些模型：困惑度（perplexity）、校准、损失地形。2025 年的两篇论文将重点转移到功能结构上：

• Jiang & Haghtalab 证明，广泛使用的神经块（neural blocks）、预 LayerNorm Transformer 层、扩散骨干（diffusion backbones）和机器人控制器作为连续映射是满射的^1。
• Nikolaou 等人证明，GPT 风格的语言模型从离散提示（prompts）到隐藏状态（hidden states）是单射的，并提供了一种可操作的反演算法^2。

乍看之下，这种组合类似于一个悖论：

“该模型可以达到每一个输出” 和 “该模型永远不会将两个提示映射到相同的表示。”

LLM 是双射的吗？这些结果是否不一致？都不是。这两个定理涉及 LLM 模型内部不同的映射，一旦我们解开它们，它们就会揭示一个连贯的画面，对安全、隐私和 AI 驱动的加密系统产生直接影响。

第一部分从第一性原理重构数学。第二部分将把这些见解应用于具体的 AI+DeFi 系统、金库管理器、治理代表、AI 预言机，并展示满射性和单射性如何改变它们的威胁模型和安全含义。

---

1. 三个功能属性，以及它们背后的几何

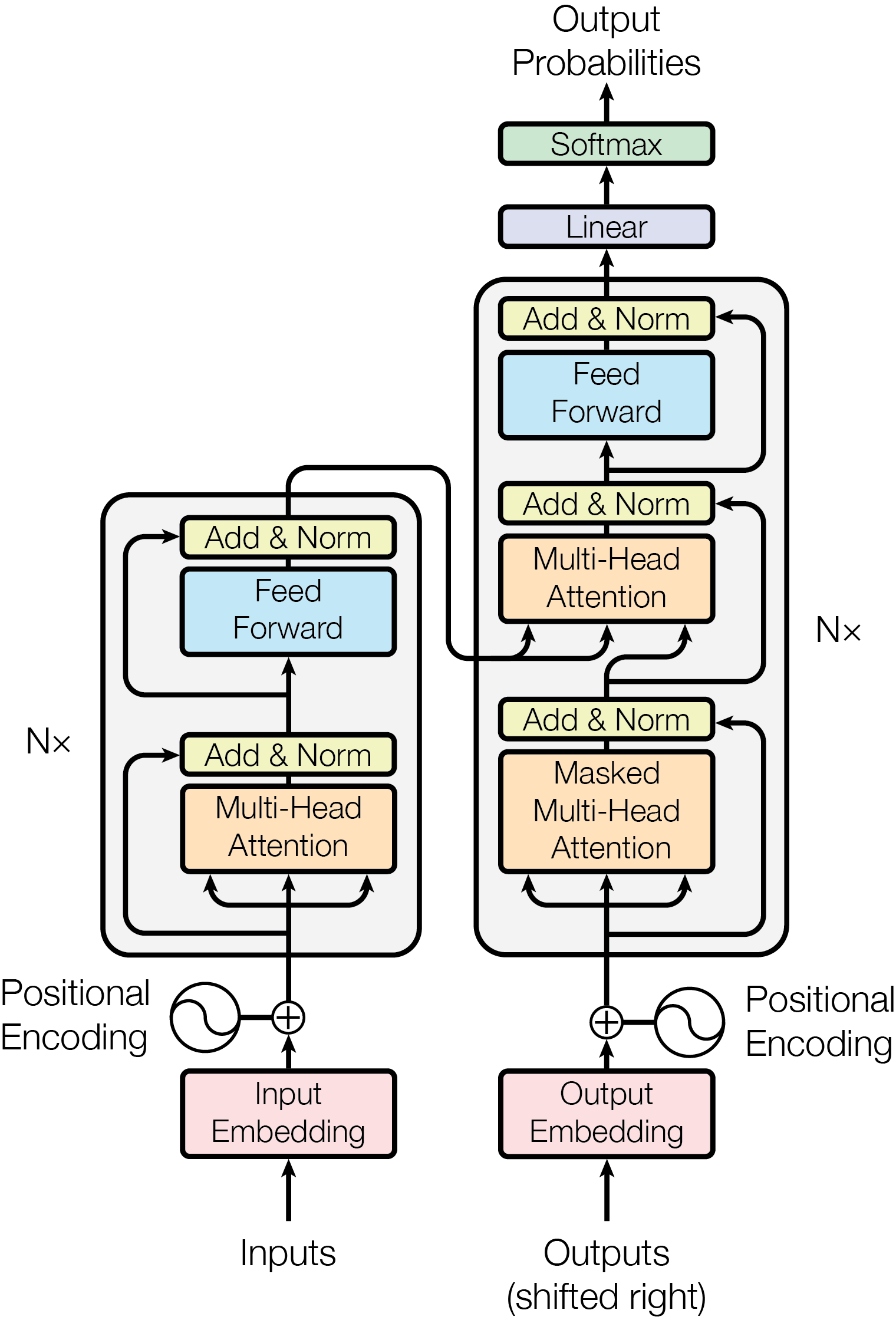来源：图 1：Transformer - 模型架构，https://arxiv.org/abs/1706.03762.

设 $f: \mathcal{X} \to \mathcal{Y}$。三个属性描述了输入空间和输出空间在 Transformer 模型 中是如何相关的。

1.1 满射性（“onto”）

如果 $$ \forall y \in \mathcal{Y},~\exists x \in \mathcal{X} \text{ 使得 } f(x) = y, $$ 则一个函数是满射的。

每个输出都可以由某个输入产生。从几何角度来看，想象一下输入平面上的一个网格。一个满射变换可能会折叠和自相交该网格，但它会覆盖整个输出平面。没有区域是无法到达的。

1.2 单射性（“one-to-one”）

如果 $$ x \neq x' \Rightarrow f(x) \neq f(x'), $$ 则一个函数是单射的。

没有一对输入碰撞到同一个输出。从几何角度来看，网格线可能会弯曲，但它们永远不会交叉；不同的点仍然是不同的。

1.3 双射性

一个既是单射又是满射的函数是双射的，并且允许一个真正的逆函数 $$ f^{-1}: \mathcal{Y} \to \mathcal{X}. $$

即使一个函数是单射的（原则上存在唯一的逆函数），计算该逆函数仍然可能是不可行的。我们研究的论文涉及：

• 满射性，但没有反演算法，以及
• 单射性，以及一种建设性的反演方法。

---

2. 一个 Transformer 包含几个不同的函数

graph TB
    subgraph " "
        P["V^≤K<br/>Prompt 空间"]
        H["ℝ^d<br/>隐藏表示"]
        O["V^≤K'<br/>输出空间"]
        E1["(ℝ^d)^n<br/>嵌入序列"]
        E2["(ℝ^d)^n<br/>转换后的嵌入"]
    end

    P -->|"F_θ (自回归 LM)"| O
    P -->|"r_θ (单射)"| H
    P -->|"tokenize & embed （分词并嵌入）"| E1
    E1 -->|"TF_θ (满射)"| E2
    E2 -->|"unembed & decode （解除嵌入并解码）"| O
    E2 -.->|"pick layer & position （选择层和位置）"| H

    style P fill:#e1f5ff,stroke:#333,stroke-width:2px
    style H fill:#fff4e1,stroke:#333,stroke-width:2px
    style O fill:#e1f5ff,stroke:#333,stroke-width:2px
    style E1 fill:#f0f0f0,stroke:#333,stroke-width:2px
    style E2 fill:#f0f0f0,stroke:#333,stroke-width:2px

    classDef legend fill:#fff,stroke:none
    L["Maps:<br/>F_θ: V^≤K → V^≤K' (自回归 LM)<br/>r_θ: V^≤K → ℝ^d (prompt → hidden, 单射)<br/>TF_θ: (ℝ^d)^n → (ℝ^d)^n (连续核心, 满射)"]:::legend

“Transformer 是满射的吗？”或“LLM 是单射的吗？”是模棱两可的，因为模型包含几个结构上不同的映射。

下面解释了其中三个重要的映射。

2.1 连续核心

$$ \mathrm{TF}_\theta : (\mathbb{R}^d)^n \to (\mathbb{R}^d)^n $$

这是纯粹在嵌入上运行的多层块结构（注意力 + MLP）。Jiang & Haghtalab 在他们的论文^1中分析了这个映射。

2.2 Prompt-to-representation 映射

设 $\mathcal{V}$ 是一个有限词汇表，$K$ 是一个上下文界限。一个仅解码的 LM 定义了 $$ r_\theta: \mathcal{V}^{\le K} \to \mathbb{R}^d, $$ 例如“prompt $\mapsto$ 某个层的最后一个位置的最终隐藏状态”。这是 Nikolaou 等人证明是单射的映射^2。

2.3 完整自回归 LM

用户面对的模型定义了 $$ F_\theta: \mathcal{V}^{\le K} \to \mathcal{V}^{\le K'}, $$ 它包括嵌入、TF 块、logit 投影、采样或 argmax，以及迭代直到 EOS。这既不是单射的也不是满射的。

公众讨论中的大多数困惑源于默默地将一个映射替换为另一个映射。满射性论文涉及 2.1；单射性论文涉及 2.2；人们经常谈论得好像两者都适用于 2.3。

---

3. 深度神经网络中的满射性：任何 Embedding 空间输出都是可达的

论文：关于神经网络的满射性：你能从你的模型中引出任何行为吗？ (Haozhe Jiang, Nika Haghtalab, 2025)^1。

现代 Transformer 块（预 LayerNorm + 残差）具有以下形式 $$ g(x) = f(\mathrm{LN}(x)) + x, $$ 其中 $f$ 是连续的，$\mathrm{LN}$ 将输入归一化到一个有界集合上。

关键结果是：

对于任何连续的 $f$，映射 $g$ 在 $\mathbb{R}^d$ 上是满射的。

这扩展到序列式映射和此类块的堆栈，从而为实际的预LN Transformer 核心提供了满射性。

3.1 论证草图

使用不动点理论证明了满射性。

1. LayerNorm 确保 $\mathrm{LN}(x)$ 位于一个紧凑集合中，因此存在 $M$，使得 $$ |f(\mathrm{LN}(x))| \le M \quad \text{对于所有 } x. $$

2. 给定一个目标 $y \in \mathbb{R}^d$，定义 $$ F_y(x) = y - f(\mathrm{LN}(x)). $$

3. 选择足够大的 $R$，使得球 $B_R = {x : |x| \le R}$ 满足 $F_y(B_R) \subseteq B_R$。直观地说，$F_y(x)$ 不能将你推出一个足够大的球，因为 $f(\mathrm{LN}(x))$ 是有界的。

4. 根据 Brouwer 不动点定理，存在 $x^ \in B_R$，使得 $$ F_y(x^) = x^*. $$

5. 重新排列得到 $$ y = f(\mathrm{LN}(x^)) + x^ = g(x^*), $$ 因此 $g$ 是满射的。

Haozhe Jiang 的论文 通过度理论将其扩展到序列输入 $(\mathbb{R}^d)^n$ 和层堆栈，涵盖了实际的 Transformer 架构。

3.2 这在实践中意味着什么

满射性是一种结构性属性；它与初始化、训练或超参数无关。这意味着：

如果一个行为对应于某个 Embedding 空间输出，那么存在一些输入可以产生它。

该证明是存在性的；它没有产生一种寻找该输入的有效方法。但从安全角度来看，仅仅存在就已经很重要了。

3.3 对于 AI+Crypto 从业者

在具有经济或物理后果的系统中，安全性由“这个输出是否会发生？”来定义。对于连续核心，满射性回答“是”：如果动作空间包含灾难性动作，则该架构不会排除它。

当一个 AI 代理控制：

• 交易向量，
• 治理投票，
• 风险参数更新，或
• 影响链上系统的机器人中的执行器命令时，

满射性结果表明，没有架构保证模型“不能做 X”。X 在典型训练数据下是否可能发生是一个不同的统计问题。

---

4. 语言模型的单射性：隐藏状态作为无损编码

论文：语言模型是单射的，因此是可逆的 (Nikolaou 等人，2025)^2。

考虑一个具有词汇表 $\mathcal{V}$、最大上下文长度 $K$ 和选择的层/位置的仅解码 Transformer，我们在该位置读取隐藏状态。对于一个 prompt $$ s = (s_1,\dots,sT) \in \mathcal{V}^{\le K}, $$ 定义 $$ r\theta(s) \in \mathbb{R}^d $$ 为该隐藏状态。

主要定理：

在合理的初始化上以概率 1（并在梯度下降下保留），映射 $r_\theta$ 是单射的。 换句话说， $$ s \neq s' \Rightarrow r\theta(s) \neq r\theta(s'). $$

因此，不同的 prompt 几乎肯定不会在表示空间中冲突。

4.1 直观图景：无损指纹

单射映射是一种无冲突编码器，这意味着：

• 每个不同的输入 prompt 都会产生一个唯一的隐藏向量；
• 没有两个 prompt 共享相同的内部状态；
• 隐藏状态包含足够的信息来唯一标识输入。

非正式地说：

隐藏状态是整个 prompt 的可逆指纹。

如果我们知道 $r_\theta$ 并且可以访问该模型，则该表示基本上决定了 prompt。

4.2 为什么这意味着隐私风险

如果观察者看到 $r_\theta(s)$，并且他们可以将该模型用作预言机，那么：

1. 他们知道它对应于一个且仅一个 prompt $s$。
2. 原则上，他们可以通过探测模型来搜索该 $s$。
3. 如果搜索过程是有效的，他们可以重建精确的输入。

用机制设计语言来说：如果类型（私有信息）通过单射函数映射到信号，那么观察信号会在模型的“世界”中确定类型。没有多对一压缩；该信号是一个完整的信息编码。

这与“内部嵌入匿名化用户数据”的通常假设相反。

4.3 SipIt：将单射性转化为实际的逆运算

该论文并没有止步于存在性^2。它介绍了 SipIt（通过迭代更新的顺序逆向 Prompt），它：

• 使用因果关系：位置 $t$ 处的隐藏状态仅取决于前缀 $(s_1,\dots,s_t)$；
• 对于固定的前缀，改变下一个 token $s_t$ 并观察 resulting 隐藏状态；
• 找到其 induced 状态与存储状态匹配的 token。

对于长度为 $T$ 的 prompt，他们表明 SipIt 可以使用最多

$$ O(T \cdot |\mathcal{V}|) $$ 模型查询来恢复 $s$。GPT-2 类似模型的实验表明，对于重要的 prompt，可以实现精确或接近精确的重建。

结果是明确的：

隐藏状态不是匿名的聚合；它们是原始文本的可逆编码。

存储或传输它们实际上等同于存储或传输 prompt。

4.4 单射性没有说什么

单射性适用于 $$ \text{prompt} \longmapsto \text{hidden state}\quad(r\theta), $$ 而不是适用于 $$ \text{prompt} \longmapsto \text{生成的文本}\quad(F\theta). $$

自回归 LM $F_\theta$：

• 不是单射的：许多 prompt 会产生相同的补全；
• 不是满射的：大多数可能的 token 序列永远不会产生。

因此，这些结果并不意味着聊天记录唯一地标识 prompt。它们确实意味着，如果你记录内部激活，你正在记录接近原始输入的内容。

---

5. 协调结果：没有双射性，没有悖论

将两个定理并排放置：

• 满射性涉及 $\mathrm{TF}_\theta: (\mathbb{R}^d)^n \to (\mathbb{R}^d)^n$。
• 单射性涉及 $r_\theta: \mathcal{V}^{\le K} \to \mathbb{R}^d$。
• 完整 LM 映射是 $F_\theta: \mathcal{V}^{\le K} \to \mathcal{V}^{\le K'}$。

只有当两个属性都应用于同一函数时，我们才能获得双射性。他们没有。该模型包含一个满射的连续核心和一个单射的离散到连续的前端，但用户面对的映射都不是。

不存在矛盾。“LLM 是双射的”这个梗是将定理错误地分配给错误的函数。

---

6. 不对称性：满射性威胁安全，单射性威胁隐私

这两个属性具有不同的安全特性。

6.1 满射性 → 通过可达性带来的安全风险

如果 AI 策略的动作空间 $\mathcal{A}$ 包含有害动作 $a_{\text{harm}}$，则满射性意味着

$$ \exists z \in \mathcal{Z}: \pi\theta(z) = a{\text{harm}}. $$

安全性是存在性定义的：如果可以达到有害输出，则系统必须假定它可能发生。寻找相应输入的难度是一个次要考虑因素。

对于以下 AI 代理：

• 签署交易，
• 调整协议参数，
• 执行治理投票，
• 或驱动其故障模式涉及链上系统的机器人，

满射性表明：只要合约的动作空间允许灾难性移动，就存在神经策略将产生它的条件。仅凭架构无法证明“代理永远不会这样做”。

6.2 单射性 → 通过可恢复性带来的隐私风险

$r_\theta$ 的单射性意味着

$$ r\theta(s) = r\theta(s') \Rightarrow s = s'. $$

内部表示是 prompt 的一对一指纹。当与诸如 SipIt 之类的有效反演算法结合使用时，这会产生隐私风险：

• 记录隐藏状态等同于记录 prompt，
• 共享嵌入可能会泄露专有数据，
• 在链上发布激活会将用户文本暴露给任何可以模拟该模型的人。

用机制设计术语来说，$r_\theta$ 将私有类型转换为完全泄露的信号。任何使用这些信号的协议都必须将它们视为包含完整的类型信息。

---

7. AI + Crypto 的含义：满射性和单射性作为设计约束

一旦 Transformer 位于密码经济系统（作为金库管理器、预言机或治理代理）中，它就不再仅仅是“一个模型”。它成为将链上和链下状态映射到具有经济后果的行动的机制的组成部分。

形式上，你可以将机制视为一个元组 $$ (\mathcal{Z}, \mathcal{A}, \pi, \text{rules}), $$ 其中 $\mathcal{Z}$ 是代理可用的信息，$\mathcal{A}$ 是行动空间（交易、参数更新、投票），$\pi$ 是由模型实现的策略，“规则”是解释这些行动的链上合约和链下程序。

满射性和单射性限制了你可以就此类系统提出的论点的种类：

• 连续核心的满射性表明：对于钱包/合约愿意执行的任何 $a \in \mathcal{A}$，都存在一些 $z \in \mathcal{Z}$，使得 $\pi_\theta(z) = a$。你没有一种结构性保证，即“代理永远不会输出 $a$”。
• prompt→representation 映射的单射性表明：如果你暴露从私有输入导出的内部表示，那么这些表示本质上等同于输入本身，至少对于任何可以近似逆的群体而言。

因此，正确的问题不是“我们如何训练模型以使其安全和私密”，而是：

我们如何构建机制，使这两个事实仍然成立，但不会伤害我们？

7.1 安全性：满射性和可接受动作的形状

连续核心的满射性 $$ \mathrm{TF}_\theta : (\mathbb{R}^d)^n \to (\mathbb{R}^d)^n $$ 表明嵌入空间中的每个输出向量都具有至少一个原像。这是体系结构的属性，而不是训练或微调的属性。从嵌入到嵌入的映射是两个全维连续空间之间的 onto 映射。

当这样的模型位于加密经济系统（金库控制器、策略模块、治理“代表”、路由组件）中时，这对于我们如何讨论安全性至关重要。为了使含义明确，将安全推理分为三个级别是有帮助的。

级别 1：基本安全性——有害动作是否完全可达？

在最基本的层面上，设计人员经常提出以下形式的问题：

• “控制器是否会提出耗尽金库的转移？”
• “预言机是否会输出远远超出合理范围的值？”
• “治理模块是否会投票赞成灾难性的更改？”

通常的非正式答案是：“不会，因为我们没有训练它这样做。”

满射性与通常的解码层结合在一起，破坏了这种论证风格。如果策略可以在其输出空间中表示一个动作（例如，通过生成解码为该动作的 logit 配置），那么通过满射性，就存在导致该配置的某个输入嵌入序列。训练可能会使该输入不寻常或难以找到，但该体系结构不会排除它。

如果合约的动作集是 $\mathcal{A}_\text{allowed}$，并且模型引发了一个映射

$$ \pi\theta : \mathcal{Z} \to \mathcal{A}\text{allowed}, $$

那么安全的默认设置是将每个 $a \in \mathcal{A}_\text{allowed}$ 视为可以从某个 $z \in \mathcal{Z}$ 到达。对于级别 1 安全性，结论很简单：

• 如果合约在语法上允许某个动作，那么应该表现得好像存在模型发出该动作的某种观察结果。

因此，安全性必须由合约（以及过滤动作的任何链上逻辑）来实施，而不是通过关于模型“永远不会做”的假设来实施。

实际上，这意味着：

• 约束合约中的行动空间（上限、速率限制、允许列表），
• 编写适用于 $\mathcal{A}_\text{allowed}$ 的每个元素的不变量，
• 并将训练时的安全工作（RLHF、微调）视为塑造典型行为，而不是作为防止极端行为的保证。

级别 2：中级安全性——哪种环境会引发不良行为？

一旦肯定地回答了“是否完全可能？”，下一个问题是：在什么条件下可以实际驱动模型采取有害动作？

在加密设置中，模型的许多输入至少部分是对抗性的或可操作的：预言机馈送、mempool 内容、链上文本、提案描述、链下新闻等等。可以影响 $\mathcal{Z}$ 部分的攻击者不受“自然”Prompt 的限制。他们可以尝试在观察空间中搜索将 $\pi\theta$ 推入他们关心的 $\mathcal{A}\text{allowed}$ 区域中的点。

满射性没有给出查找此类输入的复杂性界限，但确实改变了举证责任：你不能争辩说某些动作是安全的，因为“没有现实的输入会产生它们”，除非你对 $\mathcal{Z}$ 如何受到限制有独立的论点。

对于中级安全性，这有三个具体后果：

1. 必须强化观察接口。 并非每个外部信号都应以原始方式馈送到模型。在价格馈送、池状态和提案元数据成为模型输入的一部分之前，应对其进行范围检查、分桶、离散化和速率限制。这减少了对手可以探索的 $\mathcal{Z}$ 的有效大小。

2. 必须控制机制级别的敏感性。 合约方面可以实施单调性或有界敏感性条件。如果 $a = \pi_\theta(z)$ 并且 $z$ 在某些受控意义上发生少量变化，则实际执行的动作 $a$ 的变化应在合约层受到限制。从概念上讲，希望通过合约逻辑来限制闭环系统的有效 $\partial a / \partial z$，而不是信任网络的内部平滑性。

3. 威胁模型应该是输入的最坏情况。 为了安全起见，最好将 $\mathcal{Z}$ 视为在协议强制执行的任何语法限制内以对抗方式选择。满射性加上对 $\mathcal{Z}$ 的对抗性控制意味着应该假定可以达到有害动作，因此安全论点必须依赖于在 $\pi_\theta$ 提出动作之后发生的事情。

级别 3：专家安全性——在最坏情况下的行为下系统级别的不变性

在最高级别，问题不是是否会出现特定的不良交易，而是即使 AI 控制的模块以与其接口一致的最坏方式运行，整个系统是否可以被驱动到灾难性状态。

这是与机制设计和控制理论的联系变得至关重要的地方。假设我们简单地将 $\pi\theta$ 视为从 $\mathcal{Z}$ 到 $\mathcal{A}\text{allowed}$ 的任意函数。合约和周围的机制定义了状态演化 $$ x_{t+1} = F(x_t, a_t), \qquad at \in \mathcal{A}\text{allowed}. $$

满射性表明 $\pi_\theta$ 访问任何可接受的 $a_t$ 没有架构障碍。对于系统级别的安全性，我们 then 需要：

• 激励兼容区域，其中每个可接受的 $a_t$ 都保留了所需的经济特性（例如，所有可能的重新平衡都满足偿付能力和集中度限制），
• 以及对于所有可接受的动作序列保持为真的状态不变性，而不仅仅是对于“典型”轨迹。

用控制理论术语来说，稳定性分析必须考虑整个可接受的动作集，而不仅仅是训练数据恰好探索的子集。任何 Lyapunov 型保证或有界漂移论证都必须在合约级别强制执行。该模型被视为可接受的动作空间内的不受控制的组件。

概括这种情况的一种简洁方法是：

• AI 控制的模块的安全级别由周围机制的不变性和 $\mathcal{A}_\text{allowed}$ 的大小决定，而不是由任何关于模型“已经学会不做”的非正式信念决定。

一个小表格摘要在这里可以作为心理检查清单：

安全级别	非正式期望	满射性建议什么
基本	模型不会输出明显的不良动作。	任何语法上允许的动作都应被视为可达的。
中级	不良动作需要极端的 Prompt。	对手可以搜索输入；将 $\mathcal{Z}$ 视为对抗性的。
专家	训练和对齐提供全局安全性。	只有合约级别的不变量才能约束最坏情况的行为。

---

7.2 隐私：单射性以及内部状态揭示的内容

映射的单射性 $$ r_\theta : \mathcal{V}^{\le K} \to \mathbb{R}^d $$ 意味着在单射性定理的假设下，每个隐藏状态 $h$ 唯一地标识了 prompt $s$。与诸如 SipIt 之类的显式反演过程一起使用时，这会将内部表示转换为输入的可逆编码。当记录、共享或传递给其他系统这些表示时，会对隐私产生直接影响。

同样，将三个级别区分开来是有帮助的：是否存在任何隐私，声称的是 哪种 隐私，以及可能希望强制执行哪些正式的隐私属性。

级别 1：基本隐私——系统是否完全隐藏用户数据？

在此级别，问题是二进制的：系统是否对其他方隐藏用户输入？

在许多 ML 体系结构中，可以争辩说存储嵌入而不是原始输入至少提供了一些基本的隐私，因为多个输入可能会映射到相似的内部状态。对于单射 $r\theta$，这不再成立。如果 $h = r\theta(s)$ 并且 $r\theta$ 在相关域上是单射的，那么原则上，向任何可以近似 $r\theta^{-1}$ 的人揭示 $h$ 等效于揭示 $s$。

在 AI+DeFi 设置中，这会影响：

• 记录隐藏状态或 KV 缓存以进行调试或分析，
• 在协议之间共享嵌入“以进行互操作性”，
• 在链上缓存内部状态以提高透明度。

在单射性下，这些做法相当于发布用户的 Prompt 的可逆图像和任何其他通过模型前端馈送的信息。只有当内部状态永远不会离开 $r_\theta$ 可访问的信任边界时，此级别的基本隐私才存在。

级别 2：中级隐私——哪些隐私方面处于危险之中？

中级隐私问题区分了不同的概念：

• 是否隐藏了原始输入文本（输入隐私），
• 下游推断（风险评分、交易信号）是否泄露了太多信息（推断隐私），
• 不同的交互是否可以链接到同一用户（链接隐私），
• 以及是否只有最少必要的信息离开本地环境（数据最小化）。

单射性将这些概念结合在一起。

如果内部状态是 Prompt 的单射图像，那么：

1. 只要隐藏状态或近端替代品暴露，输入隐私就会丢失。任何发布 $h$ 或在相关集合上保持单射的线性投影的协议，实际上都会发布底层 $s$。

2. 推断隐私与输入隐私不可分离。在典型的管道中，可能会从 $h$ 计算风险评分并揭示该评分，但不揭示输入。如果 $h$ 已经泄漏，那么该评分几乎没有揭示更多信息；敏感内容已由 $h$ 确定。

3. 链接隐私是脆弱的。确定性的单射映射为相同的 $s$ 生成相同的 $h$，并为相似的 $s$ 生成附近的 $h$。即使删除了标识符，这也可以很容易地链接重复的交互或按 Prompt 的结构对用户进行聚类。

4. 如果导出的对象是可逆的，则很难争论数据最小化。除非该函数是故意破坏信息的，否则作为 $h$ 的确定性函数的小向量仍然可以保留足够的结构来重建 $s$。

为了使中间隐私声明成立，体系结构必须确保离开本地环境的任何内容都是输入的真正不可逆的转换，或者丢弃 $s$ 中包含的大部分信息的统计信息。

级别 3：专家隐私——哪些正式的隐私属性与单射性兼容？

在专家级别，人们可能会要求更正式的保证：关于观察输出会如何改变对敏感属性的信念的界限、与差异隐私相关的概念，或者关于输入的哪些特征不可恢复的可证明的陈述。

从输入到表示的确定性单射映射为每一个都带来了困难：

• 如果 $h$ 唯一地确定 $s$，则作为 $s$ 的函数的任何敏感属性也是 $h$ 的函数。观察 $h$ 等效于观察所有此类属性。

• 差异隐私通常要求数据中的微小变化在输出中产生微小的、嘈杂的变化，以便不能单独挑出个人的贡献。确定性单射变换在不同的输入之间具有严格的分离，因此其相对于更改单个输入的敏感性在相关意义上是无界的。必须在之前或代替这种变换之前通过噪声或随机化强制执行差异隐私，而不是之后。

• 特征隐私（其中输入的某些分量旨在可证明地不可恢复）与一对一编码整个输入的映射不兼容，除非在单射性之前有单独的模糊步骤。

这些观察结果不是说在使用 Transformer 的系统中不可能实现专家隐私；他们说任何合理的保证都必须来自单射前端之外的组件。示例包括破坏信息的局部预处理、不是单射的随机编码器或内部状态永远不会离开受控域的严格局部执行。

此图中的零知识证明

零知识证明通常被呈现为区块链的通用隐私工具。单射性阐明了它们在哪些方面有帮助，在哪些方面没有帮助。

如果证人是在用户的设备上组装和持有的，并且只有短的承诺或证明对象被发送到链或验证人，那么证明可以在不暴露底层数据的情况下证明属性（“我的分数高于阈值”、“此订单尊重风险限制”）。

但是，如果系统将原始 Prompt 或内部表示发送到远程证明服务，则单射性意味着证明者基本上看到了完整的输入。在这种情况下，证明可能会对链隐藏数据，但它不会对证明者隐藏数据。对于 LM 远程运行并在那里构建证人的 AI+DeFi 设计，零知识协议不会解决由单射表示引入的主要隐私风险。

架构的后果

综上所述，injectivity 为隐私至关重要的 AI+Crypto 系统带来了一些明确的设计约束：

• 内部状态和嵌入不应在协议边界之间共享或在链上发布。
• 隐藏状态的日志记录应限制在已经有权查看原始输入的环境中。
• 证明的itness 应在与 LM 相同的信任域中组装，并且只有最少的派生语句应跨越该边界。
• 如果必须传输某种形式的表示，它应该是以信息丢失为目的而设计的非可逆映射的输出（例如，粗略的 binning、clipping 或随机投影），并且它应该只编码机制实际需要的内容。

这些不是政策建议；它们是将 $r_\theta$ 视为定理所说的 injective map 的直接结果。

7.3 结合 reachability 和 reversibility

当 surjectivity 和 injectivity 共存于同一个策略 $\pi_\theta$ 内部时，整个系统会同时继承 reachable action 和 reversible input。这种组合比单独的任何一种属性都更具约束力。

以下是一些直接的观察结果。

输入 shaping 和输出 prediction 相互加强。

如果攻击者可以影响观测值，他们可以搜索 $\mathcal{Z}$ 以寻找驱动 $\pi\theta$ 朝向特定 action 的序列。如果攻击者可以恢复（或近似）$r\theta^{-1}$，他们可以观察到 agent 所看到的内容，预测可能的 action，并相应地优化他们自己的策略。

安全和隐私无法隔离。

如果机密信号通过内部表示泄漏，则依赖机密信号的机制可能会失去其预期的激励属性。同样，如果攻击者可以使用精心设计的输入来操纵 agent，而输入的结构是从 agent 状态的部分泄漏中推断出来的，那么安全假设就会失效。

系统级鲁棒性必须在机制边界上制定。

从机制的角度来看，agent 实际上是允许的输入和 action 集合中的任意函数。正确性条件必须是合约和 oracle 路径的属性，而不是关于内部网络不变性的假设。

这自然而然地引出了第二部分的架构原则。

具体示例：联合威胁下的 AI Vault Manager

为了了解这些属性如何相互作用，请考虑一个具有以下架构的 AI 控制的 DeFi vault：

系统组件： $$ \text{市场数据 } z \xrightarrow{\text{tokenize}} s \xrightarrow{r\theta} h \xrightarrow{\text{TF}\theta} h' \xrightarrow{\text{decode}} a \xrightarrow{\text{contract}} \text{execution} $$

其中 $s$ 是提示， $h$ 是隐藏状态， $h'$ 是转换后的嵌入，$a$ 是提议的 action。

威胁 1：Surjectivity 能够实现 action reachability

Vault 合约允许 action $\mathcal{A}{\text{allowed}} = {\text{rebalance}, \text{hedge}, \text{withdraw}}$。每个 action $a$ 对应于一些输出嵌入区域。通过 $\text{TF}\theta$ 的 surjectivity，对于任何 $a \in \mathcal{A}_{\text{allowed}}$，都存在一些产生它的输入嵌入。

这意味着：如果“提取 100% 到外部地址”在语法上有效，则某些市场条件 $z$（可能是对抗性精心设计的）会触发它。

威胁 2：Injectivity 能够实现输入恢复

假设 vault 记录隐藏状态 $h$ 以进行监控：

event VaultDecision(uint256 timestamp, int256[768] hiddenState, Action action);

通过 $r_\theta$ 的 injectivity，每个 $h$ 唯一地标识提示 $s$，它编码：

• 当前 vault 的仓位
• 检测到的市场情况
• 风险评估
• 计划的下一个 action

攻击者如果破坏了日志，可以反转 $h \mapsto s$ 并了解 vault 的完整内部状态和策略。

组合威胁：利用完美信息的战略操纵

现在结合这两个属性：

1. 攻击者在时间 $t$ 观察记录的 $h_t$
2. 攻击者反转以恢复 $s_t$，从而了解 vault 当前的信念和计划的 action
3. 攻击者操纵市场数据 $z_{t+1}$ 以精心设计利用此知识的输入
4. 通过 surjectivity，攻击者可以搜索 $z{t+1}$，从而驱动 vault 朝向可盈利利用的 action $a{\text{target}}$

这种组合创造了一个闭环攻击： $$ h_t \xrightarrow{\text{invert}} st \xrightarrow{\text{learn strategy}} \text{craft } z{t+1} \xrightarrow{\text{surjectivity}} a_{\text{target}} $$

架构意义：

单独的任何一个属性都不能完全确定威胁。没有可观察性（没有记录的 $h$）的 surjectivity 意味着攻击者盲目搜索。没有 surjectivity 的 injectivity 意味着泄漏的信息可能无法利用。它们共同创造了一个质量上更糟糕的威胁模型。

这就是为什么第二部分（即将推出）中的安全框架在两个边界都强制执行约束：

• 合约级别（限制 $\mathcal{A}_{\text{allowed}}$）解决 surjectivity
• 隐私边界（从不暴露 $h$）解决 injectivity

7.4 迈向稳定的设计规范

在之前建立的函数结果下，“信任边界”不能位于模型内部。它必须位于合约逻辑、观测过滤器和 AI 组件周围的密码包装器中。

具体来说：

• 合约定义并强制执行允许的 action 集合 $\mathcal{A}_\text{allowed}$。
• 观测路径约束允许的输入集合 $\mathcal{Z}_\text{trusted}$。
• 任何必须保持私有的统计信息都应在任何值暴露在信任边界之外之前计算。
• AI 模型本身被视为与连续核心中的 surjectivity 和其表示中的 injectivity 兼容的通用函数 $\pi_\theta$。

这种观点与机制设计者处理任意 agent 行为的方式相匹配：约束被施加在环境上，而不是施加在无法验证的内部计算上。

---

下一步：第二部分

此处建立的函数属性是架构事实，而不是训练产物。第二部分将这些约束转化为具体的机制：如何设计 AI+DeFi 系统，即使 surjectivity 和 injectivity 无法避免，也不会对你造成伤害。

致谢

感谢 Haozhe Jiang，Giorgos Nikolaou 以及 ^1 和 ^2 的作者们，感谢他们对深度神经网络函数属性的基础性工作。

参考文献

[^3]: Transformers 能做任何事，也能撤销它吗？

• 原文链接： github.com/thogiti/thogi...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～