ZK-SNARKS 与 Last Challenge 攻击：注意你的 Fiat-Shamir！

作者：Oana Ciobotaru, Maxim Peter 和 Vesselin Velichkov OpenZeppelin 最近在审计 Linea 的 PLONK 验证器时发现了一个严重漏洞。从本质上讲，这个问题与之前披露的一些漏洞类似（例如，Frozen Heart，00）。“Last Challenge” 漏洞源于恶意证明者在计算最终 PLONK 挑战时，利用不正确应用 Fiat-Shamir 变换所引入的自由度的能力。利用此漏洞的恶意证明者可以通过提交无效状态转换的证明来窃取 rollup 中的所有资产。虽然该问题已及时沟通并得到 修复，但我们认为具体细节值得更广泛地分享，以便其他人可以学会识别类似的模式并保护自己。 在下面详细描述该问题之前，我们将简要介绍零知识简洁非交互知识论证 (zkSNARK) 和 Fiat-Shamir 变换。

zkSNARK 的高级演练

zkSNARK 系统涉及两个方：证明者 和 验证者。证明者的目标是让验证者相信某些计算 F 的结果是正确的，并提供一个简洁的证明，该证明的验证效率高于再次执行整个计算。这在区块链的上下文中尤其有价值：节点无需重新执行所有交易来验证状态转换的有效性，而是更便宜地验证证明相同属性的 zkSNARK 证明。从理论上讲，这种证明可以为 Layer 2 (L2) 提供与在 Layer 1 (L1) 上直接执行相似的安全级别。这以延迟为代价，但具有提高可扩展性的优势。

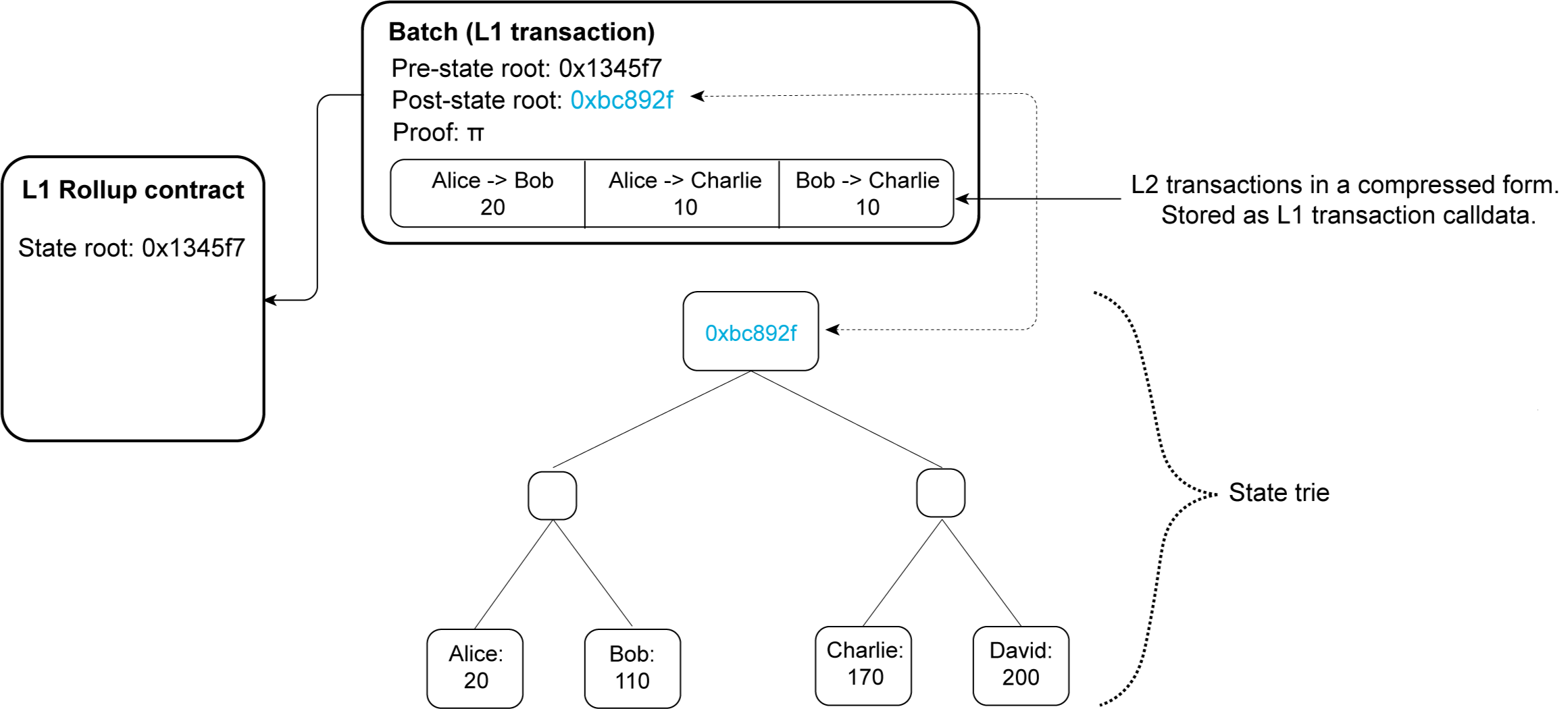
图 1：ZK rollup 的状态在其 L1 合约中更新（改编自 vitalik.ca) 上面提到的计算 F 可以表示为一个 算术电路。算术电路是一系列简单的算术运算，例如加法和乘法，也称为 门，由 线 连接。电路的输入有两种类型：公共值（公共输入），证明者和验证者都知道，以及私有值（witness），仅证明者知道，代表计算的内部值。

借助 zkSNARK，证明者在不向验证者透露 witness 的情况下证明对 witness 的了解（即，零知识 属性，保护诚实的证明者免受潜在恶意验证者的侵害），并证明计算 F 已正确执行（即，可靠性 属性，保护诚实的验证者免受潜在恶意证明者的侵害）。

下面，显示了与函数 g(x1, x2, w1) = (x1 + x2) * (x2 + w1) 对应的示例电路。对于此电路，证明者可以使用 zkSNARK 来证明，对于公共输入 (x1, x2, y) 的某些赋值，它知道 witness w1 的一个赋值，使得 g(x1, x2, w1) == y，而不透露有关 w1 的任何其他信息。

图 2：具有两个加法门和一个乘法门的算术电路的简单示例 给定这样的算术电路，可以选择适当的算术化（例如，R1CS、AIR、Plonkish），并隐式选择一种 NP 语言，为其构建 zkSNARK 方案。虽然这些细节对于任何从业者来说都很有价值，但它们不在本博客的范围内。我们推荐以下涵盖此类主题的外部资源：

• Vitalik 出色的三篇介绍性博文（第一篇、第二篇、第三篇）
• Vitalik 关于 PLONK 的博文
• LambdaClass 关于算术化的总结

更进一步，zkSNARK 系统有两个主要构建块：多项式交互预言证明 (PIOP) 和 多项式承诺方案。两者最初的形式都是 交互式的，这意味着它们作为证明者和验证者之间的一系列通信轮次进行。直观地说，PIOP（第一个版本在 PLONK 中引入，称为 多项式协议，后来在 BFS19 中推广到 PIOP）以一组多项式恒等式的形式抽象出算术电路描述的原子约束。PIOP 通过各种现有的 zkSNARK 编译器（如 PLONK、Marlin、BFS19 等中所述）编译成 zkSNARK 系统，此外还涉及多项式承诺方案。

该方案的交互性质意味着证明者和验证者在继续下一步之前必须互相等待。实际上，交互性会在步骤之间引入显着的延迟，并且要求证明者为每个新的验证者生成新的证明。

Fiat-Shamir 变换

为了避免交互性瓶颈，存在 Fiat-Shamir 变换。此变换可以应用于任何可靠且恒定轮次的 公共Coin 交互式协议，以产生功能等效、可靠且非交互式的协议。请注意，在公共Coin交互式双人协议中，交互式验证者在通信方面所做的全部工作就是计算随机挑战并将它们发送给交互式证明者。

下图给出了 Fiat-Shamir 变换的简化示例。

图 3：简化交互式协议的 Fiat-Shamir 变换 已经证明 Fiat-Shamir 变换是安全的 在 随机预言模型 中。然而，在实践中，随机预言模型由哈希函数实例化。

回到图 3 中介绍的示例，证明者和验证者都使用哈希函数来计算挑战 c，作为该实例的承诺 comf 和公共输入 x 的哈希值。这样，恶意证明者对 comf 的任何修改也会改变 c，从而阻止它选择 comf 和 c 以利于自己。

在下文中，我们将重点关注具体的 zkSNARK，即 PLONK。更具体地说，我们将研究在 Linea 的 PLONK Fiat-Shamir 变换实现中发现的错误。

PLONK

PLONK 是一种 ZK 简洁论证系统，给定一个算术电路 C，它证明一方（即证明者）知道一个与公共输入 x 对应的 witness w，使得 (x,w) 满足算术电路 C。在 PLONK 的大多数常见变体中，多项式承诺使用 KZG 多项式承诺 实例化，并且生成的证明是一组承诺（实际上，承诺是配对友好的椭圆曲线上的点）和域元素。PLONK 的交互版本包括证明者和验证者之间的几轮通信。

通过使用 Fiat-Shamir 变换，该协议可以变为非交互式的：对于每个交互轮次，非交互式 PLONK 证明者通过哈希到该轮次为止的通信 记录 来自行生成相应的挑战集。到某个轮次为止的记录定义为定义电路的公共参数、定义实例的公共输入以及到该轮次为止由 PLONK 证明者计算的证明元素的串联。本博文中检查的 PLONK 版本 是撰写本文时可用的最新版本（来自 2022 年 8 月 17 日），其中记录和在每一轮计算的相应挑战如下所示：

其中 pp 包含公共参数和公共输入，而 H 表示哈希函数。

请注意，u（最后一个挑战）未在任何 PLONK 证明者轮次中使用。事实上，u 仅由 PLONK 验证者用于批量验证两个不同评估点的多个评估。因此，理所当然地，出现了以下问题：鉴于 PLONK 验证者只需要 u 是随机的，并且 u 未被 PLONK 证明者使用，那么“注重效率”的验证者是否真的需要遵循指定的协议并将 u 计算为完整记录的哈希值？

最后的挑战攻击

在 PLONK 的情况下，不使用完整记录计算挑战会使验证者面临潜在的漏洞。例如，最后挑战攻击适用于 PLONK 验证者的实现，其中最后一个挑战 u 不是使用证明元素 [W𝔷]1 和 [W𝔷ω]1 （它们是完整记录的一部分）导出的。

在描述攻击的步骤之前，我们简要回顾一下 PLONK 验证者 的相关部分。PLONK 验证者分 12 个步骤工作，最后一个步骤表示验证以下双线性配对等式：

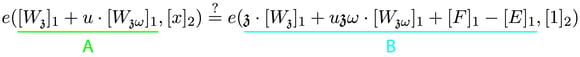
请注意，在上面的等式中，[F]1 和 [E]1 由验证者使用证明者发送的承诺和评估来计算。

最后挑战攻击的进行方式如下：

图 4：攻击的可视化演练

影响

在以太坊上的 ZK rollup 的情况下，电路模拟以太坊虚拟机 (EVM)。因此，诚实的证明者可以证明交易块已正确执行，并且某个状态转换是有效的。但是，容易受到最后挑战攻击的验证者实现使恶意证明者可以伪造无效状态转换的证明。通过这样做，恶意证明者可以将自己设置为 rollup 中所有资产的所有者。

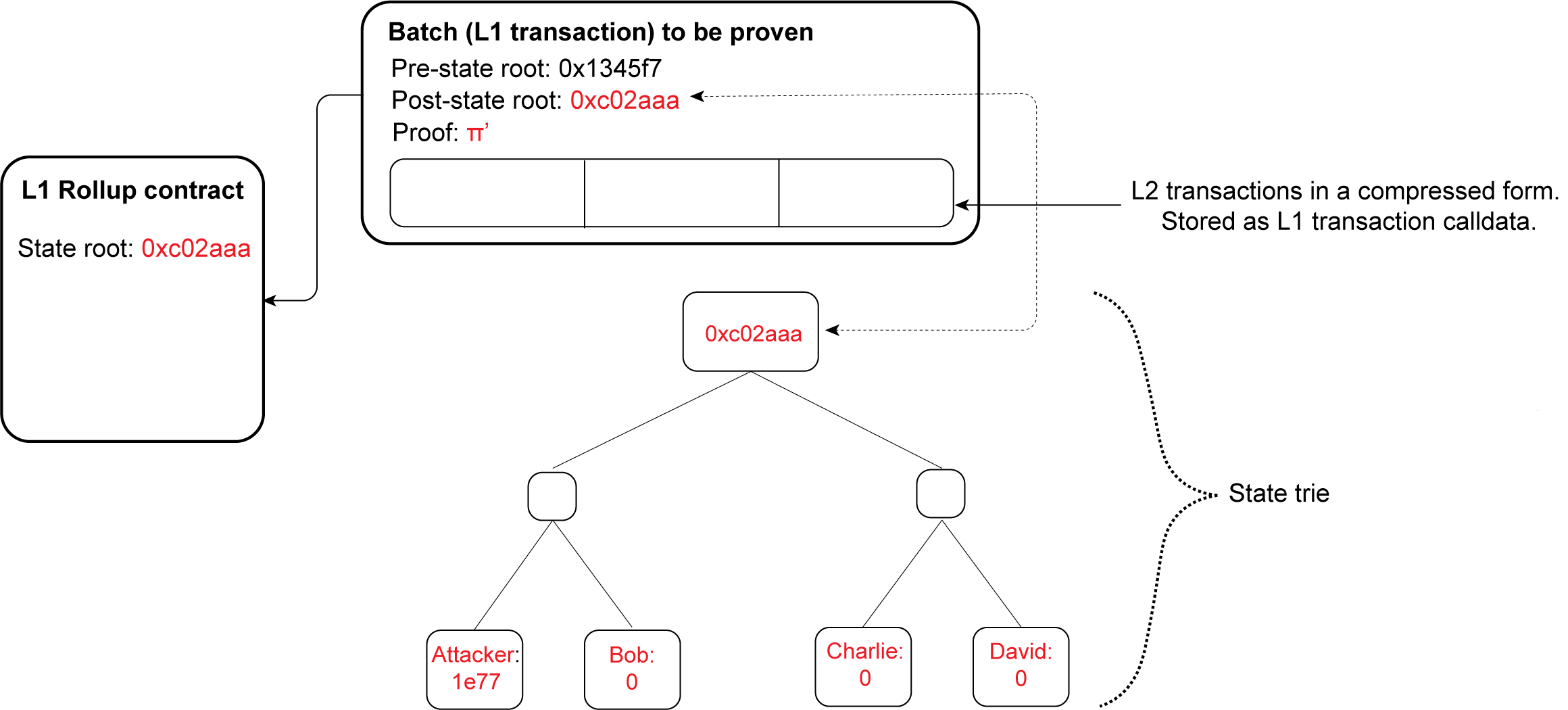
图 5：接受恶意证明后可能的 ZK rollup 状态

结论

Fiat-Shamir 变换是 zkSNARK 系统中安全漏洞的常见来源。非交互式验证者应遵循标准规范，在 PLONK 的情况下，标准规范从整个记录中导出 Fiat-Shamir 挑战。此导出确保恶意证明者对记录元素的任何更改也会修改挑战。如上所述，偏离标准规范可能会导致恶意证明者构造虚假陈述的证明，从而可能造成灾难性后果。注意你的 Fiat-Shamir！

• 原文链接： openzeppelin.com/news/th...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～