Vitalik二次算术程序：从零到英雄 - Vitalik

二次算术程序：从零到英雄

最近，zk-SNARKs 背后的技术引起了很多关注，人们越来越多地 试图揭示 许多人称之为“月球数学”的东西，因为它被认为是难以理解的复杂性。 zk-SNARKs 确实很难掌握，特别是因为整个事情需要结合多个移动部分，但如果我们逐步分解技术，那么理解就简单了。

这篇文章的目的是不做 zk-SNARKs 的全面介绍；它假设你了解 zk-SNARKs 是什么以及它们的作用，并且具有足够的数学知识来理解多项式等内容（如果语句 P(x) + Q(x) = (P + Q)(x) 看起来是自然和显而易见的，那么你就达到了正确的水平）。相反，本文深入探讨了这个技术的机制，尽可能地解释 zk-SNARK 研究员 Eran Tromer 在此处绘制的管道的前半部分：

这里的步骤可以分为两部分。首先，zk-SNARKs 不能直接应用于任何计算问题；相反，你必须将问题转换为正确的“形式”以便于操作。该形式称为“二次算术程序”（QAP），将函数的代码转换为这种形式本身就是一个相当复杂的过程。与将函数代码转换为 QAP 的过程一起，另一个过程可以并行运行，以便如果你有代码的输入，就可以创建一个对应的解决方案（有时称为 QAP 的“证人”）。之后，还有另一个相当复杂的过程，用于为这个证人创建实际的“零知识证明”，以及一个单独的过程，用于验证其他人转交给你的证明，但这些是本文不讲的细节。

我们选择的例子是一个简单的：证明你知道立方方程的解：x**3 + x + 5 == 35（提示：答案是 3）。这个问题足够简单，以至于生成的 QAP 不会大到让人害怕，但又足够不平凡，让你能够看到所有机制发挥作用。

让我们将我们的函数写为：

def qeval(x):
    y = x**3
    return x + y + 5

我们在此处使用的简单专用编程语言支持基本算术（+，-，*，/），常数次幂运算（x**7 但不是 x**y）和变量赋值，这足够强大，可以理论上在其中执行任何计算（只要计算步骤的数量是有限的；不允许循环）。请注意，不支持模运算（%）和比较运算符（<，>，≤，≥），因为在有限循环群算术中没有有效的方法来直接执行模运算或比较（对此要感激；如果有方法执行其一，那么椭圆曲线密码学将比你说“二分搜索”和“中国余数定理”更快地被打破）。

你可以通过提供位分解（例如 13 = 2**3 + 2**2 + 1）作为辅助输入来扩展语言支持模运算和比较，证明那些分解的正确性并在二进制电路中进行数学运算；在有限域算术中，进行相等性（==）检查同样是可行的，实际上也相对容易，但这些都是我们此时不打算深入探讨的细节。我们可以通过将条件转换为算术形式（例如 if x < 5: y = 7; else: y = 9），来扩展语言以支持条件语句：y = 7 * (x < 5) + 9 * (x >= 5)；不过请注意，条件的两个“路径”都需要被执行，如果你有很多嵌套条件，那么这可能会导致大量的开销。

现在让我们一步一步地进行这个过程。如果你想自己为任何一段代码做这个，我 在这里实现了一个编译器（仅出于教育目的；还没有为现实世界的 zk-SNARKs 制作 QAP 准备好！）。

扁平化

第一步是“扁平化”过程，我们将原始代码转换为一系列声明，这些声明的两种形式是：x = y（其中 y 可以是变量或数字）和 x = y (op) z（其中 op 可以是 +，-，*，/，y 和 z 可以是变量、数字或它们自身的子表达式）。你可以将每一个这些语句看作是电路中的逻辑门。上述代码的扁平化过程结果如下：

sym_1 = x * x
y = sym_1 * x
sym_2 = y + x
~out = sym_2 + 5

如果你阅读原始代码和这里的代码，你可以很容易地看出二者是等价的。

门到R1CS

现在，我们将其转换为称为秩-1约束系统（R1CS）的东西。R1CS 是一系列三元组 (a, b, c)，而 R1CS 的解决方案是一个向量 s，其中 s 必须满足方程 s . a * s . b - s . c = 0，其中. 代表点乘 - 更简单地说，如果我们将 a 和 s “压缩在一起”，将同一位置的两个值相乘，然后对这些乘积求和，再对 b 和 s 以及 c 和 s 进行相同操作，那么第三个结果等于前两个结果的乘积。例如，这是一个满意的 R1CS：

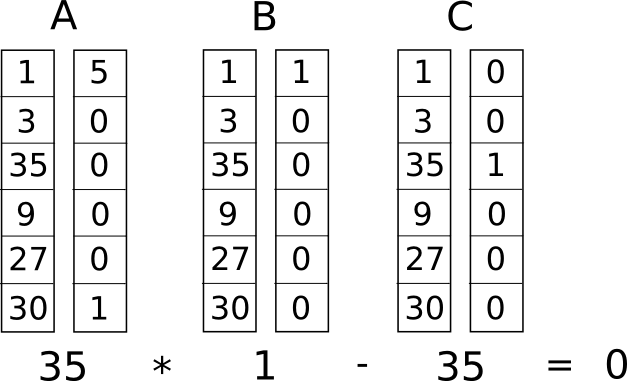
但我们不仅仅有一个约束，而是将有许多约束：每一个逻辑门一个。根据操作是（+，-，* 或 /）以及参数是变量还是数字，有标准的方法将逻辑门转换为 (a, b, c) 三元组。每个向量的长度等于系统中的总变量数，包括在第一个索引处的虚拟变量 ~one 代表数字 1，输入变量，代表输出的虚拟变量 ~out，然后是所有中间变量（上述的 sym1 和 sym2）；向量通常是非常稀疏的，只填充与某个特定逻辑门相关的变量对应的插槽。

首先，我们将提供我们将使用的变量映射：

'~one', 'x', '~out', 'sym_1', 'y', 'sym_2'

解向量将由按此顺序分配的所有这些变量组成。

现在，我们将给出第一个门的 (a, b, c) 三元组：

a = [0, 1, 0, 0, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 1, 0, 0]

你可以看到，如果解向量的第二个位置包含 3，第四个位置包含 9，无论解向量的其余内容如何，点乘检查都将归结为 3 * 3 = 9，因此它将通过。如果解向量在第二个位置为 -3，第四个位置为 9，则检查也将通过；事实上，如果解向量在第二个位置为 7，第四个位置为 49，则该检查仍然会通过 - 这个第一个检查的目的是验证第一个门输入和输出的一致性。

现在，让我们继续进行第二个门：

a = [0, 0, 0, 1, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 0, 1, 0]

与第一个点乘检查类似，这里我们检查 sym_1 * x = y。

现在，第三个门：

a = [0, 1, 0, 0, 1, 0]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 0, 0, 0, 1]

这里，模式有些不同：它将解决向量中的第一个元素与第二个元素和第五个元素相乘，之后加和这两个结果，并检查和是否等于第六个元素。由于解向量中的第一个元素始终为一，因此这只是一个加法检查，检查输出是否等于两个输入的和。

最后，第四个门：

a = [5, 0, 0, 0, 0, 1]
b = [1, 0, 0, 0, 0, 0]
c = [0, 0, 1, 0, 0, 0]

在这里，我们评估最后的检查 ~out = sym_2 + 5。点乘检查的工作原理是取解向量中的第六个元素，将其与第一个元素相乘五次（提醒一下：第一个元素是 1，所以这实际上是增加 5），并检查它与第三个元素一致，第三个元素是我们存储输出变量的地方。

于此，我们得到了四个约束的 R1CS。证人只是对所有变量的分配，包括输入、输出和内部变量：

[1, 3, 35, 9, 27, 30]

你可以自己计算这一点，只需通过“执行”上面的扁平代码，从输入变量分配 x=3 开始，在计算中将所有中间变量和输出的值放入。

完整组合的 R1CS 为：

A
[0, 1, 0, 0, 0, 0]
[0, 0, 0, 1, 0, 0]
[0, 1, 0, 0, 1, 0]
[5, 0, 0, 0, 0, 1]B
[0, 1, 0, 0, 0, 0]
[0, 1, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]
[1, 0, 0, 0, 0, 0]C
[0, 0, 0, 1, 0, 0]
[0, 0, 0, 0, 1, 0]
[0, 0, 0, 0, 0, 1]
[0, 0, 1, 0, 0, 0]

从 R1CS 到 QAP

下一步是将此 R1CS 转换为 QAP 形式，它实现相同的逻辑，只是使用多项式而不是点乘。我们这样做。我们从四组长度为六的向量转到六组三元3次多项式，其中在每个 x 坐标 处评估多项式表示一个约束。也就是说，如果我们在 x=1 处评估多项式，那么我们得到第一组向量，如果在 x=2 处评估多项式，那么我们得到第二组向量，依此类推。

我们可以使用名为 拉格朗日插值 的方法进行这种转换。拉格朗日插值解决的问题是这样的：如果你有一组点（即 (x, y) 坐标对），那么对这些点进行拉格朗日插值会给你一个通过所有这些点的多项式。我们通过分解问题来实现这一点：对于每个 x 坐标，我们创建一个在该 x 坐标处具有所需 y 坐标并在我们感兴趣的所有其他 x 坐标处的 y 坐标为 0 的多项式，然后为了得到最终结果，我们将所有多项式相加。

我们来做一个例子。假设我们想要一个通过 (1, 3)，(2, 2) 和 (3, 4) 的多项式。我们首先创建一个通过 (1, 3)，(2, 0) 和 (3, 0) 的多项式。事实证明，创建一个在 x=1 处“突出”和在其他感兴趣的点为零的多项式很简单；我们只需：

(x - 2) * (x - 3)

看起来是这样的：

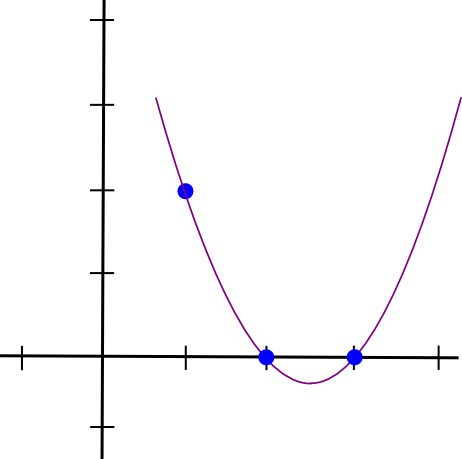
现在，我们只需将其“重新缩放”，使得在 x=1 处的高度正确：

(x - 2) * (x - 3) * 3 / ((1 - 2) * (1 - 3))

这给我们：

1.5 * x**2 - 7.5 * x + 9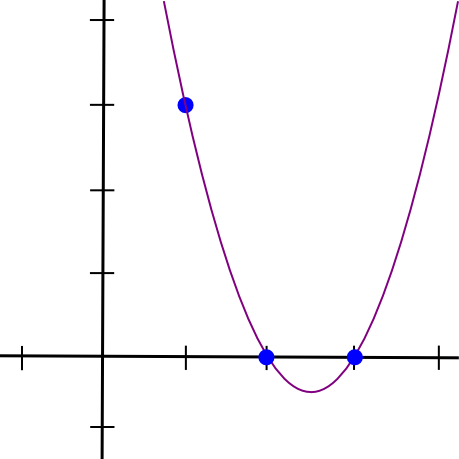

我们对另外两个点做同样的操作，得到其他两个类似形的多项式，只是它们在 x=2 和 x=3 处“突出”，而不是 x=1。我们将所有三个多项式相加得到：

1.5 * x**2 - 5.5 * x + 7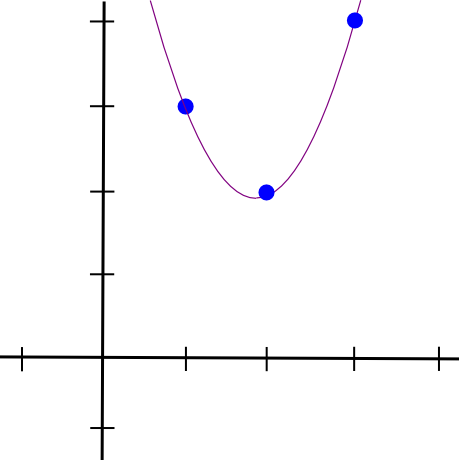

得到了确切的坐标。上述描述的算法的时间复杂度为 O(n**3)，因为有 n 个点，每个点需要 O(n**2) 的时间将多项式相乘；经过一些思考，可以将其减少到 O(n**2) 的时间，经过更多思考，使用快速傅里叶变换算法等，甚至可以进一步减少 —— 当在实践中使用的 zk-SNARK 函数通常具有成千上万的门时，这是一个至关重要的优化。

现在，让我们用拉格朗日插值来转换我们的 R1CS。我们要做的是从每个 a 向量中取得第一个值，使用拉格朗日插值将其制作成多项式（在第 i 处评估该多项式会给你第 i 个 a 向量的第一个值），然后对每个 b 和 c 向量的第一个值重复这个过程，之后对第二个值、第三个值等等重复这个过程。为了方便，我现在将答案提供出来：

A 多项式
[-5.0, 9.166, -5.0, 0.833]
[8.0, -11.333, 5.0, -0.666]
[0.0, 0.0, 0.0, 0.0]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]
[-1.0, 1.833, -1.0, 0.166]B 多项式
[3.0, -5.166, 2.5, -0.333]
[-2.0, 5.166, -2.5, 0.333]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]C 多项式
[0.0, 0.0, 0.0, 0.0]
[0.0, 0.0, 0.0, 0.0]
[-1.0, 1.833, -1.0, 0.166]
[4.0, -4.333, 1.5, -0.166]
[-6.0, 9.5, -4.0, 0.5]
[4.0, -7.0, 3.5, -0.5]

系数按升序排列，因此上面的第一个多项式实际上是 0.833 * x**3 - 5*x**2 + 9.166*x - 5。这一组多项式（加一个稍后我会解释的 Z 多项式）构成了这个特定 QAP 实例的参数。请注意，直到这一点为止的所有工作对于每个你试图使用 zk-SNARKs 验证的函数只需要执行一次；一旦 QAP 参数生成后，就可以重复使用。

让我们试着在 x=1 的时候评估所有这些多项式。在 x=1 时评估多项式意味着将所有系数相加（因为 1**k = 1 对于所有 k），所以这并不困难。我们得到：

A 在 x=1 的结果
0
1
0
0
0
0B 在 x=1 的结果
0
1
0
0
0
0C 在 x=1 的结果
0
0
0
1
0
0

果不其然，我们得到的正是我们上面为第一个逻辑门创建的三组向量。

检查 QAP

那么，这种疯狂的变换有什么意义呢？答案是，现在我们可以通过在 多项式 上进行点乘检查来同时检查 所有 约束，而不是逐个检查 R1CS 中的约束。

因为在这种情况下点乘检查是一系列多项式的加法和乘法，结果也是一个多项式。如果计算结果的多项式在我们用于表示逻辑门的每个 x 坐标处评估为零，则这意味着所有检查都通过；如果计算结果的多项式在至少一个代表逻辑门的 x 坐标的评估值为非零，则这意味着输入和输出到该逻辑门的值不一致（即，“门是 y = x * sym_1”，但提供的值可能是 x = 2，sym_1 = 2 和 y = 5）。

请注意，结果多项式本身不需要为零，实际上在大多数情况下也不会；它在与任何逻辑门无关的点可以具有任何行为，只要在所有与某些门相关的点上结果为零即可。为了检查正确性，我们无需在与每个门相对应的每个点上评估多项式 t = A . s * B . s - C . s；相反，我们通过另一个多项式 Z 来除以 t，并检查 Z 是否均匀地除尽 t——也就是说，除法 t / Z 不留下余数。

Z 定义为 (x - 1) * (x - 2) * (x - 3) ... ——在所有与逻辑门相对应的点上为零的最简单多项式。一个代数的基本事实是，=O 任何在所有这些点上为零的多项式都必须是这个最小多项式的倍数，如果多项式是 Z 的倍数，则它在任何这些点的评估将为零；这种等价性使我们的工作变得简单得多。

现在，让我们实际执行上述多项式的点乘检查。首先，中间多项式：

A . s = [43.0, -73.333, 38.5, -5.166]
B . s = [-3.0, 10.333, -5.0, 0.666]
C . s = [-41.0, 71.666, -24.5, 2.833]

现在，A . s * B . s — C . s：

t = [-88.0, 592.666, -1063.777, 805.833, -294.777, 51.5, -3.444]

现在，最小多项式 Z = (x - 1) * (x - 2) * (x - 3) * (x - 4)：

Z = [24, -50, 35, -10, 1]

如果我们用上述结果除以 Z，得到：

h = t / Z = [-3.666, 17.055, -3.444]

没有余数。

因此，我们得到了 QAP 的解决方案。如果我们尝试伪造从中推导出此 QAP 解决方案的 R1CS 解中的任何变量——比如将最后一个设置为 31 而不是 30，那么我们得到一个在某个检查上失败的 t 多项式（在这种特定情况下，x=3 时的结果为 -1 而不是 0），而且进一步地，t 将不作为 Z 的倍数；相反，除以 t / Z 将得到余数 [-5.0, 8.833, -4.5, 0.666]。

请注意，上述是简化；“在现实世界中”，加法、乘法、减法和除法不是用常规数字，而是用有限域元素进行的——这是一种自洽的算术，其中我们知道并热爱的代数法则仍然适用，但所有答案都是某个有限大小集合的元素，通常是从 0 到 n-1 的整数。例如，如果 n = 13，则 1 / 2 = 7（且 7 * 2 = 1），3 * 5 = 2，等等。使用有限域算术消除了担心舍入误差的需要，并允许系统与椭圆曲线良好地配合，而椭圆曲线最终在 zk-SNARK 机制的其余部分中是必要的，使 zk-SNARK 协议在实际中是安全的。

特别感谢 Eran Tromer 帮助我解释了关于 zk-SNARK 内部工作机制的许多细节。

• 原文链接： medium.com/@VitalikButer...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～