Fiat-Shamir 启发式非交互式零知识证明之美（以及 Zig）

本文介绍了使用 Zig 编程语言实现基于 Fiat-Shamir 启发式的非交互式零知识证明（NIZKP），并结合有限域算术运算，通过示例代码详细展示了如何在 secp256k1 曲线以及 NIST P256、Ristretto255、Edwards25519 和 P384 曲线上验证 Peggy 知道秘密 x，同时比较了使用有限域和标量值进行计算的不同方法。

使用 Fiat-Shamir 启发法的非交互式零知识证明之美 (以及 Zig)

我喜欢使用 Zig，其中最强大的方法之一是有限域 (FF) 的集成，我们可以在定义的限制内执行算术运算。使用椭圆曲线时，这由曲线的阶定义。那么，让我们用 Zig 实现具有非交互式 (NI) ZKP（零知识证明）的 Fiat-Shamir 启发法，并使用有限域进行计算。

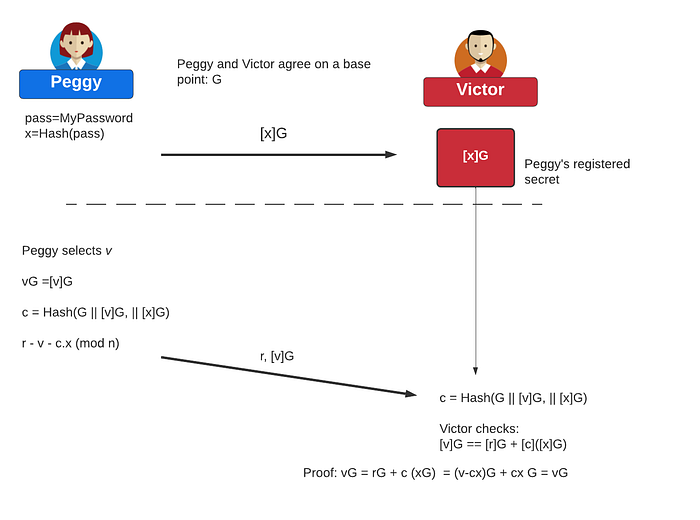
非交互式零知识证明 (ZKP)

我们使用 Fiat-Shamir 启发法来证明 Peggy 知道一个秘密 $x$。她会将 $[x]G$ 发送给 Victor 以注册她的秘密。为了证明 Peggy 仍然知道 $x$，她创建一个随机值 $v$，并计算椭圆曲线点：

$V =[v]G$

接下来，她从 $G$（曲线上的基点）、$[v]G$ 和 $[x]G$ 的哈希创建自己的挑战：

$c =$ Hash($G || vG || xG$)

然后她计算：

$r =(v − c.x) \pmod n$

其中 $n$ 是曲线的阶。她将 $V$、$r$ 和 $c$ 的值发送给 Victor，Victor 计算：

$Vcheck =[r]G +c$

如果 $V$ 等于 $Vcheck$，则 Peggy 已经证明她知道 $x$。这是因为：

$Vcheck =[r]G +c=[r]G +[c.x]G =[v − c.x]G +[c.x]=[v]G −[cx]G +[cx]G = vG$

这可以表示为：

源代码

以下代码使用 Zig Version 0.15.1 编译 [ here][ code]：

const std = @import("std");
const crypto = @import("std").crypto;

pub fn main() !void {
    var stdout_buffer: [4096]u8 = undefined;
    var stdout_writer = std.fs.File.stdout().writer(&stdout_buffer);
    const stdout = &stdout_writer.interface;
    // create a seed for key pair generation
    // 为密钥对生成创建一个种子
    var secret: []const u8 = undefined;
    const args = try std.process.argsAlloc(std.heap.page_allocator);
    defer std.process.argsFree(std.heap.page_allocator, args);
    // Check if there are any arguments
    // 检查是否有任何参数
    if (args.len > 1) {
        secret = args[1];
    }

    var hash256: [crypto.hash.sha2.Sha256.digest_length]u8 = undefined;
    crypto.hash.sha2.Sha256.hash(secret, &hash256, .{});
    var x: [32]u8 = undefined;
    crypto.random.bytes(&x);
    const G = crypto.ecc.Secp256k1.basePoint;
    const xG = try crypto.ecc.Secp256k1.basePoint.mul(x, std.builtin.Endian.big);

    // Random value v, and compute [v]G
    // 随机值 v，并计算 [v]G
    var v: [32]u8 = undefined;
    crypto.random.bytes(&v);
    const vG = try crypto.ecc.Secp256k1.basePoint.mul(v, std.builtin.Endian.big);

  // Compute c=H(G || [x]G || [v]G)
  // 计算 c=H(G || [x]G || [v]G)
    var chal: [crypto.hash.sha2.Sha256.digest_length]u8 = undefined;
    var hasher = crypto.hash.sha2.Sha256.init(.{});
    hasher.update(G.toCompressedSec1()[0..32]);
    hasher.update(xG.toCompressedSec1()[0..32]);
    hasher.update(vG.toCompressedSec1()[0..32]);
    hasher.final(&chal);

    const N = crypto.ff.Modulus(256);

   // Set to the order of the secp256k1 curve
   // 设置为 secp256k1 曲线的阶
    const n = try N.fromPrimitive(u256, 115792089237316195423570985008687907852837564279074904382605163141518161494337);
    const c = try N.Fe.fromBytes(n, &chal, std.builtin.Endian.big);
    const xval = try N.Fe.fromBytes(n, &x, std.builtin.Endian.big);
    const vval = try N.Fe.fromBytes(n, &v, std.builtin.Endian.big);

    // r=v - cx
    // r=v - cx
    const cx = n.mul(c, xval);
    const r = n.sub(vval, cx);
    var rval: [32]u8 = undefined;
    try r.toBytes(rval[0..32], std.builtin.Endian.big);

    const rG = try crypto.ecc.Secp256k1.basePoint.mul(rval, std.builtin.Endian.big);
    const cxG = try crypto.ecc.Secp256k1.mul(xG, chal, std.builtin.Endian.big);

    // Vcheck = [r]G + [cx]G
    // Vcheck = [r]G + [cx]G
    const Vcheck = crypto.ecc.Secp256k1.add(rG, cxG);

    try stdout.print("Fiat Shamir ZKP with secp256k1\n", .{});
    try stdout.print("\nSecret (x) = {s}\n", .{secret});
    try stdout.print("\nH(x) = {x}\n", .{x});
    try stdout.print("\nc = {!}\n", .{c.toPrimitive(u256)});
    try stdout.print("\nr = {!}\n", .{r.toPrimitive(u256)});
    try stdout.print("\nxG = {x}\n", .{xG.toCompressedSec1()});
    try stdout.print("\nvG = {x}\n", .{vG.toCompressedSec1()});
    try stdout.print("\nVcheck = {x}\n", .{Vcheck.toCompressedSec1()});

    if (Vcheck.equivalent(vG)) {
        try stdout.print("ZKP has been proven (Vcheck==vG)!\n", .{});
    } else {
        try stdout.print("ZKP has NOT been proven (Vcheck!=vG)!\n", .{});
    }

    try stdout.flush();
}

在 Microsoft Windows 上，我们使用以下命令编译为可执行文件：

> zig build-exe zig_zkp.zig

然后我们可以运行文件 zig_skp.exe。用于哈希 “Qwerty123!!” 的示例运行 [ code]：

Secret (x) = Qwerty123!!

H(x) = 0699ba0602e676d11ffa070e10d45a03479619253f5422d30c0abb5a5a5a4477

c = 71314918198815654483741033944527316465794307287640183335572333466974548625485

r = 90992810232267076410012670116849349083581283123157794062713642774154053910008

xG = 0386eb3a550e243b2229ccbaeee11d8a4adddcfcd91704f368d7eef534a3591a80

vG = 03b27f05c79867608a8f8d469289170f4413ed8d7bcfc955c9411ac56e2a2fb88a

Vcheck = 03b27f05c79867608a8f8d469289170f4413ed8d7bcfc955c9411ac56e2a2fb88a

ZKP has been proven (Vcheck==vG)!

在代码中，我们使用与 secp256k1 曲线相关的有限域。这将确保我们执行与曲线阶数相关的算术运算。对于 secp256k1，阶数 ($n$) 由以下设置：

// Set to the order of the secp256k1 curve
// 设置为 secp256k1 曲线的阶
const n = try N.fromPrimitive(u256, 115792089237316195423570985008687907852837564279074904382605163141518161494337);

const c = try N.Fe.fromBytes(n, &chal, std.builtin.Endian.big);
const xval = try N.Fe.fromBytes(n, &x, std.builtin.Endian.big);
const vval = try N.Fe.fromBytes(n, &v, std.builtin.Endian.big);

它将 $x$ 和 $v$ 的值限制到 secp256k1 的有限域中。然后使用以下公式计算 $r$ 的值：

// r=v - cx
// r=v - cx
const cx = n.mul(c, xval);
const r = n.sub(vval, cx);

使用标量而不是有限域

执行有限域数学的改进方法是用标量值来实现，例如 [ here]：

    // r = v - c.x
    // r = v - c.x
    const cx = try crypto.ecc.Secp256k1.scalar.mul(chal, x, std.builtin.Endian.big);
    const r = try crypto.ecc.Secp256k1.scalar.sub(v, cx, std.builtin.Endian.big);

然后代码变为 [ here]：

const std = @import("std");
const crypto = @import("std").crypto;

pub fn main() !void {
    var stdout_buffer: [4096]u8 = undefined;
    var stdout_writer = std.fs.File.stdout().writer(&stdout_buffer);
    const stdout = &stdout_writer.interface;

    // create a seed for key pair generation
    // 为密钥对生成创建一个种子

    var secret: []const u8 = undefined;
    const args = try std.process.argsAlloc(std.heap.page_allocator);
    defer std.process.argsFree(std.heap.page_allocator, args);

    // Check if there are any arguments
    // 检查是否有任何参数
    if (args.len > 1) {
        secret = args[1];
    }

    var hash256: [crypto.hash.sha2.Sha256.digest_length]u8 = undefined;
    crypto.hash.sha2.Sha256.hash(secret, &hash256, .{});

    var x: [32]u8 = undefined;
    crypto.random.bytes(&x);

    const G = crypto.ecc.Secp256k1.basePoint;

    const xG = try crypto.ecc.Secp256k1.basePoint.mul(x, std.builtin.Endian.big);

    // Random value v, and compute [v]G
    // 随机值 v，并计算 [v]G
    var v: [32]u8 = undefined;
    crypto.random.bytes(&v);
    const vG = try crypto.ecc.Secp256k1.basePoint.mul(v, std.builtin.Endian.big);

    // Compute c=H(G || [x]G || [v]G)
    // 计算 c=H(G || [x]G || [v]G)
    var chal: [crypto.hash.sha2.Sha256.digest_length]u8 = undefined;
    var hasher = crypto.hash.sha2.Sha256.init(.{});
    hasher.update(G.toCompressedSec1()[0..32]);
    hasher.update(xG.toCompressedSec1()[0..32]);
    hasher.update(vG.toCompressedSec1()[0..32]);
    hasher.final(&chal);

    // r = v - c.x
    // r = v - c.x
    const cx = try crypto.ecc.Secp256k1.scalar.mul(chal, x, std.builtin.Endian.big);
    const r = try crypto.ecc.Secp256k1.scalar.sub(v, cx, std.builtin.Endian.big);

    const rG = try crypto.ecc.Secp256k1.basePoint.mul(r, std.builtin.Endian.big);
    const cxG = try crypto.ecc.Secp256k1.mul(xG, chal, std.builtin.Endian.big);

    // Vcheck = [r]G + [cx]G
    // Vcheck = [r]G + [cx]G
    const Vcheck = crypto.ecc.Secp256k1.add(rG, cxG);

    try stdout.print("Fiat Shamir ZKP with Secp256k1\n", .{});
    try stdout.print("\nSecret (x) = {s}\n", .{secret});
    try stdout.print("\nH(x) = {x}\n", .{x});
    try stdout.print("\nc = {x}\n", .{chal});
    try stdout.print("\nr = {x}\n", .{r});
    try stdout.print("\nxG = {x}\n", .{xG.toCompressedSec1()});
    try stdout.print("\nvG = {x}\n", .{vG.toCompressedSec1()});
    try stdout.print("\nVcheck = {x}\n", .{Vcheck.toCompressedSec1()});

    if (Vcheck.equivalent(vG)) {
        try stdout.print("\nZKP has been proven (Vcheck==vG)!\n", .{});
    } else {
        try stdout.print("\nZKP has NOT been proven (Vcheck!=vG)!\n", .{});
    }
    try stdout.flush();
}

这是使用 NIST P256 曲线的另一种实现：

https://asecuritysite.com/zig/zig_zkp2

对于 Ristretto255 组：

https://asecuritysite.com/zig/zig_zkp3

对于 Edwards25519 组：

https://asecuritysite.com/zig/zig_zkp4

对于 P384 曲线：

https://asecuritysite.com/zig/zig_zkp5

  • 原文链接： medium.com/asecuritysite...
  • 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～
点赞 0
收藏 0
分享
本文参与登链社区写作激励计划 ，好文好收益，欢迎正在阅读的你也加入。

0 条评论

请先 登录 后评论
asecuritysite
asecuritysite
江湖只有他的大名，没有他的介绍。

asecuritysite

如果觉得我的文章对您有用，请随意打赏。你的支持将鼓励我继续创作！