区块链中的数学 - sigma协议与Fiat-Shamir变换
- blocksight
- 发布于 2021-05-05 12:49
- 阅读 11799
本文介绍Sigma协议的交互和非交互性质,简单明了,介绍了零知识证明中常用的Fiat-Shamir变换
写在前面
上一篇介绍了零知识证明的概念及性质, 没有举常见的数独,地图染色的例子,这些可以自行搜索了解,
本文继续讲sigma协议,具备一定零知识性质的协议!
Sigma协议9
设关系 $R\subseteq X * Y$, 那么<P, V> 构建在R上的一个Sigma 协议为:
P是一个叫证明的交互式协议,其输入为一个witness-statement对$(x,y)\in R$. V是一个叫验证的交互式协议,其输入为一个statement,$y \in R$.
P和V交互过程为:
- 首先,P计算一个承诺(commitment) t ,将其发送给V;
- 在收到来自P的消息后,V在有限的挑战空间C中随机选取一个挑战元素(challenge) c,并将其发送给P ;
- 在接收到来自V的挑战后, P计算出一个反馈(response) z ,将其发送给V
- 在收到了来自P的反馈后, V输出accept或者reject。
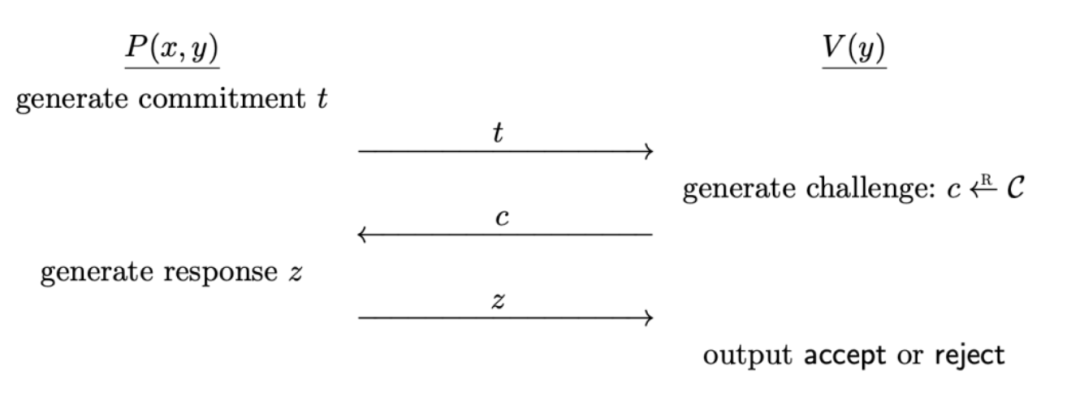
抽象定义往往让人费解,举例说明!
举例说明
以指数运算为例, p为素数,q为p − 1,的最大素数因子,g 为$Z^*_p$ 中order为q的元素,某x是P的秘密, 详细流程: 1)P计算 $h =g^x\ mod\ p$, 作为承诺给V
2)P选择随机数$r ∈ z_q $,计算$a = g^r\ mod\ p$, P将a值发送给V
3) V选择随机数challenge e,V将e值发送给P;
4) P计算$z = r + ex\ mod\ q$, 将z值发送给V,
5) V判断 $g^z=? =ah^e\ mod\ p$是否成立,若成立,则V接受认为P确实知道正确的x.
sigma协议又称为诚实验证者的(特殊)零知识证明。即假设验证者是诚实的。这个例子类似Schnorr身份认证协议,只是后者通常采用非交互的方式。
正确性(completeness)
在上面的协议中,正确性意味着如果每个人都遵守协议,那么协议正常执行。在Sigma协议的中,这意味着P和V这么做,V最后应该接受状态。
公平性(special soundness)
公平性意味着P不能证明一个错误的陈述statement. Sigma协议实现公平的。准确地说,特殊公平性!特殊公平性是说,如果P能让V在挑战中找到两个挑战,那么这两个挑战分别是(e,z)和(e′,z′)。通过代数计算【幂除法】可以得到 $𝑑 =(e-e')^1 $, 即$ x = 𝑑⋅(𝑠 − 𝑠^′)$。这样计算出x那么只能满足其中一个等式。
零知识性 (special honest verifier zk)
V既不能从协议中知道x的值,而且还不能向第三者,证明V知道这个秘密(即V无法冒充P)。也就是V从协议中什么也没学到(除了P知道x之外)。
Fiat-Shamir变换
交互式方式有其应用局限,比如得双方或多方同时在线等。Fiat-Shamir变换,又叫Fiat-Shamir Heurisitc(启发式),或者Fiat-Shamir Paradigm(范式),是Fiat和Shamir在1986年提出的一个变换,其特点是可以将交互式零知识证明转换为非交互式零知识证明。这样就通过减少通信步骤而提高了通信的效率!
该算法允许将交互步骤中随机挑战替换为非交互随机数预言机(Random oracle)。 随机数预言机,即随机数函数,是一种针对任意输入得到的输出之间是相互独立切均匀分布的函数。理想的随机数预言机并不存在,通常采用伪随机数(PRNG)在工程代码中,经常采用密码学哈希函数作为随机数预言机。
看下非交互式sigma协议: 1)P计算 $h =g^x\ mod\ p$, 作为秘密
2)P选择随机数$r ∈z_q$ ,计算$a = g^r\ mod\ p$, P将a值发送给V
3)P计算 $e = Hash(h, a)$;
4) P计算$z = r + ex\ mod\ q$, 将z值发送给V,
5) V判断 $g^z=? = ah^e\ mod\ p$是否成立,同时检验e的哈希结果是否正确,都通过后,则V接受认为P确实知道正确的x.
小结
本文介绍Sigma协议的交互和非交互性质,简单明了,介绍了零知识证明中常用的Fiat-Shamir变换,Sigma协议还有一些变种和用途,下节再说吧!
如果你觉得不够简单明了,说明基础还欠缺,耐心把之前文章看下,合抱之木,生于毫末,百尺之台起于累土!!
参考: https://www.cs.au.dk/~ivan/Sigma.pdf https://www.crypto.ethz.ch/publications/files/CamSta97b.pdf
原文链接:https://mp.weixin.qq.com/s/LHuRAA1RPzbccKHZ1wdU6g 欢迎关注公众号:blocksight
相关阅读
区块链中的数学 - 何谓零知识证明?零知识证明的概念及性质
区块链中的数学 - RSA累加器的非成员证明 RSA Accumulator非成员证明
区块链中的数学 - Accumulator(累加器) 累加器与RSA Accumulator
区块链中的数学 - Kate承诺batch opening Kate承诺批量证明
区块链中的数学 - 多项式承诺 多项式知识和承诺
区块链中的数学 - Pedersen密钥共享 Pedersen 密钥分享
区块链中的数学 - Pedersen承诺 密码学承诺--Pedersen承诺
区块链中的数学 - 不经意传输 不经意传输协议
区块链中的数学 - RSA算法加解密过程及原理 RSA加解密算法
区块链中的数学 - BLS门限签名 BLS m of n门限签名
区块链中的数学 - BLS密钥聚合 BLS密钥聚合
Schorr签名与椭圆曲线 Schorr签名与椭圆曲线
区块链中的数学-Uniwap自动化做市商核心算法解析 Uniwap核心算法解析(中)
- ZK编年史:哈希登场 162 浏览
- Layer Zero 发布 Zero 链:去中心化的多核世界计算机 367 浏览
- “Jolt Inside” - 构建者需要了解的全新武器 290 浏览
- 以太坊的下一个重大转变:从重新执行每笔交易到验证 ZK 证明 382 浏览
- Zcash:比特币遗忘的隐私 436 浏览
- ZK编年史:计算模型 302 浏览
- lambdaworks 2026 年更新路线图和优先级 371 浏览
- 2026年构建机构级DeFi平台真正需要什么 914 浏览
- zkMesh:2026年1月回顾 457 浏览
- 如果它能编译,那它就是正确的(几乎):Lean 4 在 ZK 系统和工程中的介绍 655 浏览
- Zcash 的时代到来了 785 浏览
- ZK 编年史:电路(第二部分) 425 浏览

