区块链中的数学 - Halo2 Circuit
- blocksight
- 发布于 2021-09-06 10:10
- 阅读 6480
本文介绍另一种基于plonk的proof system--halo2,目前看到基于plonk的工程实现有三种:bellman, dusk, halo2.
写在前面
上一篇介绍了Baby Jubjub 曲线,对椭圆曲线感兴趣的朋友可以看看,一种snark友好的曲线。
本文介绍另一种基于plonk的proof system--halo2,目前看到基于plonk的工程实现有三种:bellman, dusk, halo2. dusk实现接近于paper,其代码也导读过(最近几个月code有所change,可能会有变化),感兴趣可查阅过往plonk视频, bellman做了一定custom变化。halo2工程设计颇有特点!
Halo2 Proof System
Halo 2基于PLONK底层算法和电路构造模式,同时扩展自定义门(custom gate)和lookup(AKA UltraPLONK),
halo2电路书写形式与其他不同(如bellman),采用table或matrix组织定义不同属性值。是根据值的矩形矩阵定义的。使用传统的含义来表示该矩阵的行、列和单元格。
电路包含一系列配置:
- 有限域F,其中单元格(cell)值,是F的元素,使用Pasta曲线域。
-
数据存放在table中,列有几种:
- advice:就是我们常说的witness,电路中的秘密输入
- instance:作为public input, 简称PI,是P和V两方都知道(或者说共享)的值
- Fixed:作为常量(constant)使用,plonk paper中的$q_c$, 电路的一部分
- Selector: 确定gate是何种门等,在halo2中作为Fixed 列的一种特殊情况,只能取0或1
- Copy constrain 作用到两个或以上不同的cell上
- lookup&多项式约束: 约束可以是当前行的给定列中的单元格值,也可以是该行相对的另一行的给定列,即一个门中的多项式约束可以引用多行多列的值,提供了访问灵活性。
如何构造halo2中的table(or matrix),举例电路说明常见r1cs 或者其他plonk电路-->table演化
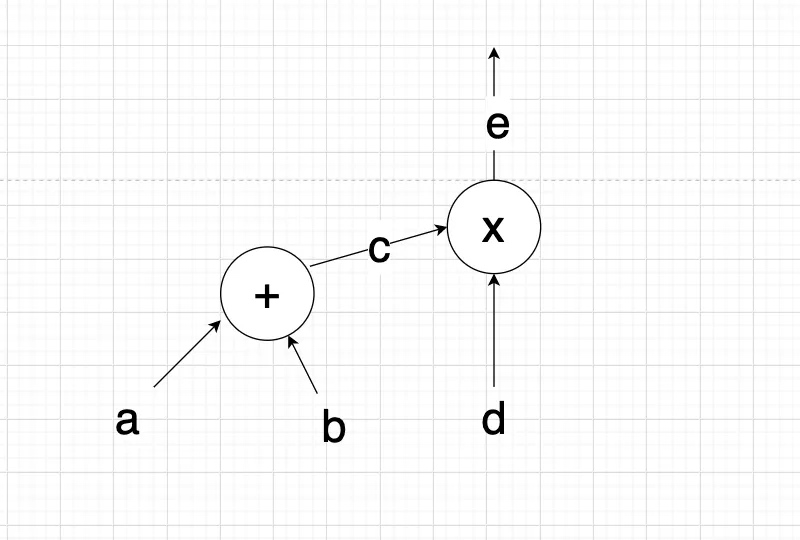
如图,构造一个简单电路描述,包含两个约束: a + b = c c * d = e
可以构造表如下:
| advice | advice | advice | selector(add) | selector(mul) |
|---|---|---|---|---|
| a | b | c | 1 | |
| c | d | e | 0 | 1 |
表中两行分别表示了上述两个约束方程,第一行满足 a + b - c = 0 , 第二行满足 c * d - e = 0 . 其中还隐含了一个复制约束,column[2][0] = column[0][1]
电路构造实例
halo2 文档中给了一个example, 验证 $a^2+b^2=c$ 其中c是public input ,即instance列值。
- 第一步:定义instruction,就是定义需要实现的方法接口,由于计算涉及到乘法,需要mul方法,同时需要加载输入变量和公共输入。
trait NumericInstructions<F: FieldExt>: Chip<F> {
/// Variable representing a number.
type Num;
Loads a number into the circuit as a private input.
fn load_private(&self, layouter: impl Layouter<F>, a: Option<F>) -> Result<Self::Num, Error>;
/// Loads a number into the circuit as a fixed constant.
fn load_constant(&self, layouter: impl Layouter<F>, constant: F) -> Result<Self::Num, Error>;
/// Returns `c = a * b`.
fn mul(
&self,
layouter: impl Layouter<F>,
a: Self::Num,
b: Self::Num,
) -> Result<Self::Num, Error>;
/// Exposes a number as a public input to the circuit.
fn expose_public(
&self,
layouter: impl Layouter<F>,
num: Self::Num,
row: usize,
) -> Result<(), Error>;
}`load_private就是加载witness, expose_public是设置instance列
2. 第二步:定义config, 代码中chip指实现特定功能且可复用的模块,粒度可大可小,比如本例子中的chip就是非常小的。config中包含运算所需要的列。
/// Chip state is stored in a config struct. This is generated by the chip
/// during configuration, and then stored inside the chip.
#[derive(Clone, Debug)]
struct FieldConfig {
/// For this chip, we will use two advice columns to implement our instructions.
/// These are also the columns through which we communicate with other parts of
/// the circuit.
advice: [Column<Advice>; 2],
/// This is the public input (instance) column.
instance: Column<Instance>,
// We need a selector to enable the multiplication gate, so that we aren't placing
// any constraints on cells where `NumericInstructions::mul` is not being used.
// This is important when building larger circuits, where columns are used by
// multiple sets of instructions.
s_mul: Selector,
/// The fixed column used to load constants.
constant: Column<Fixed>,
}3. 第三步:实现chip, 其中最重要的是 configur方法,用来构造table column和gate 约束。
impl<F: FieldExt> FieldChip<F> {
fn construct(config: <Self as Chip<F>>::Config) -> Self {
Self {
config,
_marker: PhantomData,
}
}
fn configure(
meta: &mut ConstraintSystem<F>,
advice: [Column<Advice>; 2],
instance: Column<Instance>,
constant: Column<Fixed>,
) -> <Self as Chip<F>>::Config {
meta.enable_equality(instance.into());
meta.enable_constant(constant);
for column in &advice {
meta.enable_equality((*column).into());
}
let s_mul = meta.selector();
// Define our multiplication gate!
meta.create_gate("mul", |meta| {
// To implement multiplication, we need three advice cells and a selector
// cell. We arrange them like so:
//
// | a0 | a1 | s_mul |
// |-----|-----|-------|
// | lhs | rhs | s_mul |
// | out | | |
//
// Gates may refer to any relative offsets we want, but each distinct
// offset adds a cost to the proof. The most common offsets are 0 (the
// current row), 1 (the next row), and -1 (the previous row), for which
// `Rotation` has specific constructors.
let lhs = meta.query_advice(advice[0], Rotation::cur());
let rhs = meta.query_advice(advice[1], Rotation::cur());
let out = meta.query_advice(advice[0], Rotation::next());
let s_mul = meta.query_selector(s_mul);
// Finally, we return the polynomial expressions that constrain this gate.
// For our multiplication gate, we only need a single polynomial constraint.
//
// The polynomial expressions returned from `create_gate` will be
// constrained by the proving system to equal zero. Our expression
// has the following properties:
// - When s_mul = 0, any value is allowed in lhs, rhs, and out.
// - When s_mul != 0, this constrains lhs * rhs = out.
vec![s_mul * (lhs * rhs - out)]
});
FieldConfig {
advice,
instance,
s_mul,
constant,
}
}
}4. 第四步:对chip实现第一步中定义的instruction接口
/// A variable representing a number.
#[derive(Clone)]
struct Number<F: FieldExt> {
cell: Cell,
value: Option<F>,
}
impl<F: FieldExt> NumericInstructions<F> for FieldChip<F> {
type Num = Number<F>;
fn load_private(
&self,
mut layouter: impl Layouter<F>,
value: Option<F>,
) -> Result<Self::Num, Error> {
let config = self.config();
let mut num = None;
layouter.assign_region(
|| "load private",
|mut region| {
let cell = region.assign_advice(
|| "private input",
config.advice[0],
0,
|| value.ok_or(Error::SynthesisError),
)?;
num = Some(Number { cell, value });
Ok(())
},
)?;
Ok(num.unwrap())
}
fn load_constant(
&self,
mut layouter: impl Layouter<F>,
constant: F,
) -> Result<Self::Num, Error> {
let config = self.config();
let mut num = None;
layouter.assign_region(
|| "load constant",
|mut region| {
let cell = region.assign_advice_from_constant(
|| "constant value",
config.advice[0],
0,
constant,
)?;
num = Some(Number {
cell,
value: Some(constant),
});
Ok(())
},
)?;
Ok(num.unwrap())
}
fn mul(
&self,
mut layouter: impl Layouter<F>,
a: Self::Num,
b: Self::Num,
) -> Result<Self::Num, Error> {
let config = self.config();
let mut out = None;
layouter.assign_region(
|| "mul",
|mut region: Region<'_, F>| {
// We only want to use a single multiplication gate in this region,
// so we enable it at region offset 0; this means it will constrain
// cells at offsets 0 and 1.
config.s_mul.enable(&mut region, 0)?;
// The inputs we've been given could be located anywhere in the circuit,
// but we can only rely on relative offsets inside this region. So we
// assign new cells inside the region and constrain them to have the
// same values as the inputs.
let lhs = region.assign_advice(
|| "lhs",
config.advice[0],
0,
|| a.value.ok_or(Error::SynthesisError),
)?;
let rhs = region.assign_advice(
|| "rhs",
config.advice[1],
0,
|| b.value.ok_or(Error::SynthesisError),
)?;
region.constrain_equal(a.cell, lhs)?;
region.constrain_equal(b.cell, rhs)?;
// Now we can assign the multiplication result into the output position.
let value = a.value.and_then(|a| b.value.map(|b| a * b));
let cell = region.assign_advice(
|| "lhs * rhs",
config.advice[0],
1,
|| value.ok_or(Error::SynthesisError),
)?;
// Finally, we return a variable representing the output,
// to be used in another part of the circuit.
out = Some(Number { cell, value });
Ok(())
},
)?;
Ok(out.unwrap())
}
fn expose_public(
&self,
mut layouter: impl Layouter<F>,
num: Self::Num,
row: usize,
) -> Result<(), Error> {
let config = self.config();
layouter.constrain_instance(num.cell, config.instance, row)
}
}- 使用实现的chip构建电路
/// The full circuit implementation.
/// In this struct we store the private input variables. We use `Option<F>` because
/// they won't have any value during key generation. During proving, if any of these
/// were `None` we would get an error.
#[derive(Default)]
struct MyCircuit<F: FieldExt> {
constant: F,
a: Option<F>,
b: Option<F>,
}
impl<F: FieldExt> Circuit<F> for MyCircuit<F> {
// Since we are using a single chip for everything, we can just reuse its config.
type Config = FieldConfig;
type FloorPlanner = SimpleFloorPlanner;
fn without_witnesses(&self) -> Self {
Self::default()
}
fn configure(meta: &mut ConstraintSystem<F>) -> Self::Config {
// We create the two advice columns that FieldChip uses for I/O.
let advice = [meta.advice_column(), meta.advice_column()];
// We also need an instance column to store public inputs.
let instance = meta.instance_column();
// Create a fixed column to load constants.
let constant = meta.fixed_column();
FieldChip::configure(meta, advice, instance, constant)
}
fn synthesize(
&self,
config: Self::Config,
mut layouter: impl Layouter<F>,
) -> Result<(), Error> {
let field_chip = FieldChip::<F>::construct(config);
// Load our private values into the circuit.
let a = field_chip.load_private(layouter.namespace(|| "load a"), self.a)?;
let b = field_chip.load_private(layouter.namespace(|| "load b"), self.b)?;
// Load the constant factor into the circuit.
let constant =
field_chip.load_constant(layouter.namespace(|| "load constant"), self.constant)?;
// We only have access to plain multiplication.
// We could implement our circuit as:
// asq = a*a
// bsq = b*b
// absq = asq*bsq
// c = constant*asq*bsq
//
// but it's more efficient to implement it as:
// ab = a*b
// absq = ab^2
// c = constant*absq
let ab = field_chip.mul(layouter.namespace(|| "a * b"), a, b)?;
let absq = field_chip.mul(layouter.namespace(|| "ab * ab"), ab.clone(), ab)?;
let c = field_chip.mul(layouter.namespace(|| "constant * absq"), constant, absq)?;
// Expose the result as a public input to the circuit.
field_chip.expose_public(layouter.namespace(|| "expose c"), c, 0)
}
}完整代码可从下方”本文参考“中找到!
小结
需要说明的一点,构造的table不一定需要所有单元格都填满数据,可能一些表格是空的(或者默认值),到这里可以总结下halo2与其他实现方案的不同点:
- halo2 电路中每个门的约束范围不一定都是某一行的元素,也可以是不同行列的元素,通过offset/rotation指定不同cell,这一点与其他算术门工程实现由很大不同,也是其灵活度的表现
- halo2中的每个门,多项式约束可以是多个,所以对门的概念理解有所不同,不能根据门的使用数量来作为衡量算法复杂度的唯一因素,还需要结合其他因素整合考虑(i.e. table宽度,degree等)。
- 原生halo2实现并不使用Kate 承若方案,但是需要时候也可以改造支持,目前已经在进行中。
本文参考: the halo2 book: https://zcash.github.io/halo2/concepts/proofs.html
halo2 repo: https://github.com/zcash/halo2
原文链接:https://mp.weixin.qq.com/s/01H6X1iT0kATn8ev-0A7-A 欢迎关注公众号:blocksight
相关阅读:
区块链中的数学--PLookup PLookup
区块链中的数学 -- Accumulator(累加器) 累加器与RSA Accumulator
区块链中的数学 - Kate承诺batch opening Kate承诺批量证明
区块链中的数学 - 多项式承诺 多项式知识和承诺
区块链中的数学 - Pedersen密钥共享 Pedersen 密钥分享
区块链中的数学 - Pedersen承诺 密码学承诺--Pedersen承诺
区块链中的数学 - 不经意传输 不经意传输协议
区块链中的数学 - RSA算法加解密过程及原理 RSA加解密算法
区块链中的数学 - BLS门限签名 BLS m of n门限签名
Schorr 签名基础篇 Schnorr签名与椭圆曲线
区块链中的数学-Uniwap自动化做市商核心算法解析 Uniwap核心算法解析(中)
- ZK编年史:哈希登场 59 浏览
- Layer Zero 发布 Zero 链:去中心化的多核世界计算机 296 浏览
- “Jolt Inside” - 构建者需要了解的全新武器 247 浏览
- 以太坊的下一个重大转变:从重新执行每笔交易到验证 ZK 证明 326 浏览
- Zcash:比特币遗忘的隐私 405 浏览
- ZK编年史:计算模型 281 浏览
- lambdaworks 2026 年更新路线图和优先级 333 浏览
- 2026年构建机构级DeFi平台真正需要什么 815 浏览
- zkMesh:2026年1月回顾 413 浏览
- 如果它能编译,那它就是正确的(几乎):Lean 4 在 ZK 系统和工程中的介绍 595 浏览
- Zcash 的时代到来了 707 浏览
- ZK 编年史:电路(第二部分) 405 浏览

