以太坊黄皮书学习笔记
- ripwu
- 发布于 2021-10-24 00:10
- 阅读 6250
此前学习以太坊黄皮书的笔记,结合 go-ethereum 源码,并且杂合了一些测试和脚本以加深理解
这是此前学习以太坊黄皮书的笔记,因为结合了 go-ethereum 源码,并且笔记中杂合了一些测试和脚本以加深理解,结果笔记比较混乱..
最近觉得还是稍微整理发出来,抛砖引玉~
版本基于 VERSION 80085f7 – 2021-07-11
黄皮书混用了 $=$ 和 $\equiv$,时而表示赋值,时而表示等价指代,注意区分
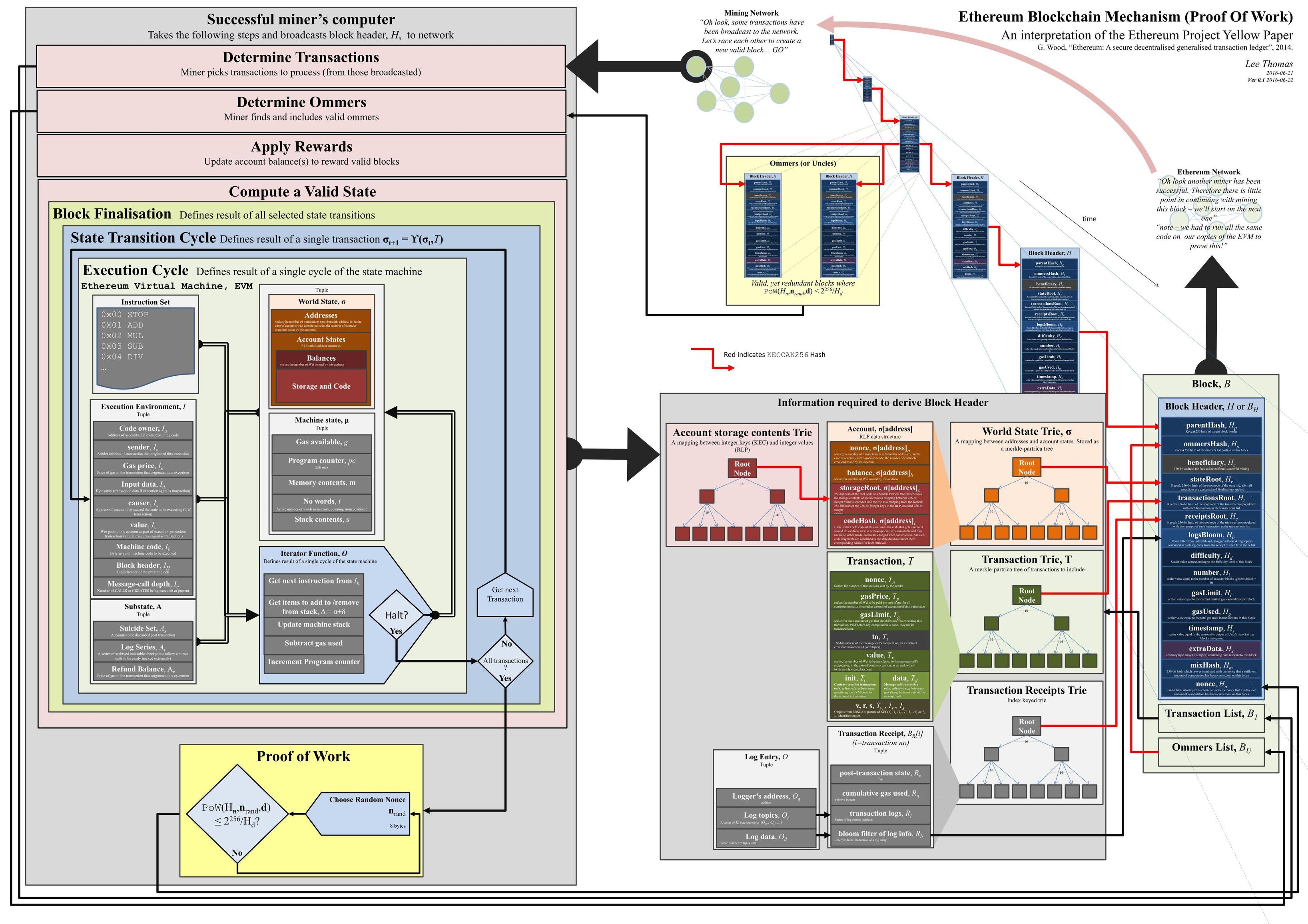
2. The Blockchain Paradigm 区块链范式
以太坊可以看作是一个交易驱动的状态机
公式 (1)
$$ \boldsymbol{\sigma}{t+1} \equiv \Upsilon(\boldsymbol{\sigma}{t}, T) $$
其中
- $ \Upsilon $ 某次状态转移的函数
- $ {\sigma} $ 状态
挖矿
- 挖矿
- 通过付出一定的工作量,与其他潜在区块竞争 一系列交易(一个区块) 的记账权
- 系统激励
- 以状态转换函数的形式,给指定账户增加 ETH
公式 (2) (3) (4)
$$ \begin{aligned} \boldsymbol{\sigma}{t+1} & \quad\equiv\quad {\Pi}(\boldsymbol{\sigma}{t}, B) \ B & \quad\equiv\quad (..., (T_0, T_1, ...), ...) \ \Pi(\boldsymbol{\sigma}, B) & \quad\equiv\quad {\Omega}(B, {\Upsilon}(\Upsilon(\boldsymbol{\sigma}, T_0), T_1) ...) \end{aligned} $$
其中
- $\Omega$ 区块奖励状态转换函数,参考公式 (169) (170) (171) (172)
- $B$ 表示一个区块,包含一系列交易和一些其他组成部分
- $ \Pi $ 区块状态转换函数,参考公式 (177)
2.2 Which History? 如何选择历史?
agreed-upon scheme
- blocktree 区块树
- 去中心化
- 每个参与者都有机会在前一个区块后,自己创建一个新的区块
- 形成一棵树(blocktree)
- 共识
- 如何从根节点到叶节点形成一条区块链
- 分叉
- 无法达成共识
- 各节点认可的 根节点到叶节点的路径(最佳区块链) 不同
(5)
$$ \beta = 1 $$
$\beta$ chain ID,参考 EIP-155: Simple replay attack protection
3. Conventions 约定
符号
- $\boldsymbol{\sigma}$ 世界状态(world-state)
- $\boldsymbol{\mu}$ 虚拟机状态(machine-state)
- $\Upsilon$ 状态转换函数
- $C$ 费用,例如$C_\text{SSTORE}$ 是执行
SSTORE操作的费用 - $\texttt{KEC}$ Keccak-256
- $T$ 一笔以太坊交易
- $n$ nonce 用于防止重放攻击
- $\mathbf{o}$ 消息调用的输出
- $\mathbb{B}_{32}$ 长度为32的字节序列
- $\mathbb{N}_{256}$ 所有比 2^256 小的正整数
- $\boldsymbol{\mu}_{\mathbf{s}}[0]$ 虚拟机栈(stack)的栈顶元素
- $\boldsymbol{\mu}_{\mathbf{m}}[0..31]$ 虚拟机内存(memory)中的前32个条目
- $\delta$某个 opcode 的出栈个数
状态
熟悉下面三种表示方式,对于后文理解状态转换非常关键
- $\Box$ 原始值/状态
- $\Box'$ 最终值/状态
- $\Box^*$, $\Box^{**}$, ... 中间值/状态
函数
公式 (6) $\ell$ 求序列的末尾元素
$$ \ell(\mathbf{x}) \equiv \mathbf{x}[\lVert \mathbf{x} \rVert - 1] $$
4. Blocks, State and Transactions 区块,状态与交易
4.1 World Stage 世界状态
参考
世界状态
- 维护 账户地址 及其 账户状态 的映射
- $a$
- 账户地址
- 大小为160位(20字节)
- $\boldsymbol{\sigma}[a]$
- 账户状态
- 含义
- 编码方式 RLP
- Recursive Length Prefix
- 递归长度前缀编码
- 用于序列化数据后传递到网络或存储
- 注意
- 世界状态不直接存储在区块链上
$\boldsymbol{\sigma}[a]$ 账户状态
- $\boldsymbol{\sigma}[a]_{\mathrm{n}}$
- nonce
- 含义
- 如果账户是钱包地址(非合约账户),表示由此账户发出的交易数量
- 如果账户是智能合约,表示由此账户创建的合约数量
- $\boldsymbol{\sigma}[a]_{\mathrm{b}}$
- balance
- 余额
- $\boldsymbol{\sigma}[a]_{\mathrm{s}}$
- storageRoot
- 含义
- 如果账户是智能合约
- 每个账户有自己的一棵 MRT 树,存储合约的内部状态(变量)
- MPT (Merkle Patricia Tree)
- Merkle Tree + Patricia Tree
- storageRoot 就是树的根节点
- $\boldsymbol{\sigma}[a]_{\mathrm{c}}$
- codeHash
- 含义
- 账户持有的代码 bytecode 的 hash
- 创建后不可被修改
- 没有代码表示智能合约
- 推导
- 用 $b$ 来表示 代码
- 则 $\texttt{KEC}(\mathbf{b}) = \boldsymbol{\sigma}[a]_{\mathrm{c}}$
公式 (7)
$$ \texttt{TRIE}\big(L{\mathrm{I}}^*(\boldsymbol{\sigma}[a]{\mathbf{s}})\big) \quad\equiv\quad \boldsymbol{\sigma}[a]_{\mathrm{s}} $$
其中
${\sigma}[a]_{\mathbf{s}}$ 表示账户的所有内部状态组成的 TRIE 树的根节点
对这棵树的所有节点做坍塌转换,即可得到根节点的 hash 值
其中 公式 (8) (9)
$$ L_{\mathrm{I}}\big( (k, v) \big) \quad\equiv\quad \big(\texttt{KEC}(k), \texttt{RLP}(v)\big) $$
$$ k \in \mathbb{B}_{32} \quad \wedge \quad v \in \mathbb{N} $$
(10) 世界状态坍塌函数 $L_{\mathrm{S}}$
$$ L_{\mathrm{S}}(\boldsymbol{\sigma}) \quad\equiv\quad { p(a): \boldsymbol{\sigma}[a] \neq \varnothing } $$
其中 公式 (11)
$$ p(a) \quad\equiv\quad \big(\texttt{KEC}(a), \texttt{RLP}\big( (\boldsymbol{\sigma}[a]{\mathrm{n}}, \boldsymbol{\sigma}[a]{\mathrm{b}}, \boldsymbol{\sigma}[a]{\mathrm{s}}, \boldsymbol{\sigma}[a]{\mathrm{c}}) \big) \big) $$
--
函数 $L_{\mathrm{S}}$ 和 Trie 函数一起用来提供一个世界状态的简短标识(hash)
我们假定:
公式 (12)
$$ \forall a: \boldsymbol{\sigma}[a] = \varnothing \; \vee \; (a \in \mathbb{B}_{20} \; \wedge \; v(\boldsymbol{\sigma}[a])) $$
公式 (13) $v$ 表示账户有效性的验证函数
$$ v(x) \quad\equiv\quad x{\mathrm{n}} \in \mathbb{N}{256} \wedge x{\mathrm{b}} \in \mathbb{N}{256} \wedge x{\mathrm{s}} \in \mathbb{B}{32} \wedge x{\mathrm{c}} \in \mathbb{B}{32} $$
其中
- $x_{\mathrm{n}}$ nonce
- $x_{\mathrm{b}}$ balance
- $x_{\mathrm{s}}$ storageRoot
- $x_{\mathrm{c}}$ codeHash
公式 (14)
$$ \mathtt{EMPTY}(\boldsymbol{\sigma}, a) \equiv \boldsymbol{\sigma}[a]{\mathrm{c}} = \texttt{KEC}\big(()\big) \wedge \boldsymbol{\sigma}[a]{\mathrm{n}} = 0 \wedge \boldsymbol{\sigma}[a]_{\mathrm{b}} = 0 $$
EMPTY 账户
- 没有 code
- 且 nonce 为0
- 且 balance 为0
公式 (15)
$$ \mathtt{DEAD}(\boldsymbol{\sigma}, a) \quad\equiv\quad \boldsymbol{\sigma}[a] = \varnothing \vee \mathtt{EMPTY}(\boldsymbol{\sigma}, a) $$
DEAD 账户
- 账户对应的状态不存在
- 或者它是 EMPTY 账户
4.2 The Transaction 交易
两种交易类型
- 消息调用 message call
- 合约创建 contract creation
共同字段
- $T_{\mathrm{n}}$
- nonce
- 由交易发送者发送的交易数量
- $T_{\mathrm{p}}$
- gasPrice
- gas 单位价格
- $T_{\mathrm{g}}$
- gasLimit
- 执行这个交易的最大 gas
- $T_{\mathrm{t}}$
- to
- 交易接收地址
- $T_{\mathrm{v}}$
- value
- 含义
- 如果是消息调用交易
- 转移到交易接收者的 wei 的数量
- 如果是合约创建交易
- 对新建合约的捐款
- $T{\mathrm{w}}$ , $T{\mathrm{r}}$ , $T_{\mathrm{s}}$
- v, r, s
- 含义
- ECDSA 签名的3个组成部分
- 可以从中推导交易发起者 from address
特有字段
- $T_{\mathrm{i}}$
- init
- 交易类型
- 合约创建
- 含义
- 是一段 EVM-code,它将返回 body,这是这个账户每次接收到消息调用时回执行的代码
- init 代码仅在合约创建时被执行一次,然后就被丢弃
- $T_{\mathrm{d}}$
- data
- 交易类型
- 消息调用
- 含义
- 用于指定消息调用的输入数据
公式 (16)
$$ L{\mathrm{T}}(T) \quad\equiv\quad \begin{cases} (T{\mathrm{n}}, T{\mathrm{p}}, T{\mathrm{g}}, T{\mathrm{t}}, T{\mathrm{v}}, T{\mathbf{i}}, T{\mathrm{w}}, T{\mathrm{r}}, T{\mathrm{s}}) & \text{if} \; T{\mathrm{t}} = \varnothing\ (T{\mathrm{n}}, T{\mathrm{p}}, T{\mathrm{g}}, T{\mathrm{t}}, T{\mathrm{v}}, T{\mathbf{d}}, T{\mathrm{w}}, T{\mathrm{r}}, T{\mathrm{s}}) & \text{otherwise} \end{cases} $$
在这里,我们假设除了任意长度的字节数组 $T{\mathrm{i}}$ 和 $T{\mathrm{d}}$ 以外,所有变量都是作为整数来进行 RLP 编码
公式 (17)
$$ \begin{aligned} & T{\mathrm{n}} \in \mathbb{N}{256} & \quad\wedge\quad & T{\mathrm{v}} \in \mathbb{N}{256} & \quad\wedge\quad & T{\mathrm{p}} \in \mathbb{N}{256} \quad \wedge \ & T{\mathrm{g}} \in \mathbb{N}{256} & \quad\wedge\quad & T{\mathrm{w}} \in \mathbb{N}{256} & \quad\wedge\quad & T{\mathrm{r}} \in \mathbb{N}{256} \quad \wedge \ & T{\mathrm{s}} \in \mathbb{N}{256} & \quad\wedge\quad & T{\mathbf{d}} \in \mathbb{B} & \quad\wedge\quad & T{\mathbf{i}} \in \mathbb{B} \end{aligned} $$
其中
公式 (18)
$$ \mathbb{N}_{\mathrm{n}} = { P: P \in \mathbb{N} \wedge P < 2^n } $$
公式 (19)
$$ T{\mathbf{t}} \in \begin{cases} \mathbb{B}{20} & \text{if} \quad T{\mathrm{t}} \neq \varnothing \ \mathbb{B}{0} & \text{otherwise}\end{cases} $$
对于合约创建交易,$T_{\mathrm{t}}$ 是 空字节 的 RLP
4.3 The Block 区块
$Block$
- $H$
- 当前区块的区块头
- $\mathbf{T}$
- 当前区块内的一系列交易
- $\mathbf{U}$
- 当前区块内的叔块头列表
$H$ (block header)
- $H_{\mathrm{p}}$
- parentHash
- 父区块 block header 的 hash
- $H_{\mathrm{o}}$
- ommersHash
- 当前区块的叔块列表的 hash
- $H_{\mathrm{c}}$
- beneficiary
- 因为挖到当前区块而获得奖励收益的账户地址
- $H_{\mathrm{r}}$
- stateRoot
- state trie 根节点的 hash
- 交易被执行完且区块定稿后的状态
- 区块内的所有交易得到的状态,组成一棵树
- $H_{\mathrm{t}}$
- transactionsRoot
- transaction trie 根节点的 hash
- 当前区块中所有交易组成的一棵树 $H_{\mathrm{e}}$
- receiptsRoot
- receipt trie 根节点的 has
- 当前区块中所有交易的收据组成的一棵树
- $H_{\mathrm{b}}$
- logsBloom
- 当前区块中所有交易的收据数据中的可索引信息(产生日志的地址和日志主题)组成的 Bloom 过滤器
- $H_{\mathrm{d}}$
- difficulty
- 含义 当前区块的难度水平 根据前一个区块的难度水平和时间戳计算得到
- $H_{\mathrm{i}}$
- number
- 当前区块的祖先的数量
- $H_{\mathrm{l}}$
- gasLimit
- 目前每个区块的 gas 开支上限
- $H_{\mathrm{g}}$
- gasUsed
- 当前区块中所有交易所用掉的 gas 之和
- $H_{\mathrm{s}}$
- timestamp
- 当前区块初始化时的 Unix 时间戳
- $H_{\mathrm{x}}$
- extraData
- 含义
- 与当前区块相关的任意字节数据
- 必须在 32 字节以内
- $H_{\mathrm{m}}$
- mixHash
- 含义
- 一个 hash 值
- 用于与 $H_{\mathrm{n}}$ 一起证明当前区块已经承载了足够的计算量
- $H_{\mathrm{n}}$
- nonce
- 含义
- 一个64位的随机整数
- 用于与 $H_{\mathrm{m}}$ 一起证明当前区块已经承载了足够的计算量
- 注意
- 这里的 nonce 是个随机数,与账户下的 nonce 定义不同
公式 (20)
$$ B \quad\equiv\quad (B{\mathrm{H}}, B{\mathbf{T}}, B_{\mathbf{U}}) $$
4.3.1 Transaction Receipt 交易收据
每个交易一定会有一条对应的收据
$R$
- Transaction Receipt
- 含义
- 每个交易执行过程中的特定信息,会被编码为交易收据
- 用途
- 零知识证明
- 索引
- 搜索
- $B_{\mathbf{R}}[i]$
- 当前区块第 i 个交易的收据
$H_{\mathrm{e}}$
- receiptsRoot
- 含义
- 区块内的收据组成 receipt trie
- 其根节点的 hash 存储在 $H_{\mathrm{e}}$ 中
公式 (21)
$$ R \quad\equiv\quad (R{\mathrm{z}}, R{\mathrm{u}}, R{\mathrm{b}}, R{\mathbf{l}}) $$
$R$ 一条收据的组成
- $R_{\mathrm{u}}$
- 当前区块中,交易发生后的累积 gas 使用量
- $R_{\mathrm{l}}$
- 交易过程中创建的一系列日志
- $R_{\mathrm{b}}$
- 256字节大小的 hash
- 由一系列日志构成的 Bloom 过滤器
- $R_{\mathrm{z}}$
- 交易的状态码
公式 (22)
$$ R_{\mathrm{z}} \in \mathbb{N} $$
公式 (23)
$$ R{\mathrm{u}} \in \mathbb{N} \quad \wedge \quad R{\mathrm{b}} \in \mathbb{B}_{256} $$
公式 (24)
$$ O \quad\equiv\quad (O{\mathrm{a}}, ({O{\mathbf{t}}}0, {O{\mathbf{t}}}1, ...), O{\mathbf{d}}) $$
只有被调用的智能合约,自身显式调用 LOG0,LOG1,LOG2,LOG3,LOG4 才会生成日志
$R_{\mathrm{l}}$
- 由一系列日志组成
- $(O_0,O_1,...)$
$O$ 一条日志的组成
- $O_{\mathrm{a}}$
- 当前被调用的智能合约的地址 (一定不会包括 EOA 地址)
- 跟随消息调用上下文变化
- 例子
- EOA -> ContracA -> ContractB -> ContractC
- $O_{\mathrm{t}}$
- 一系列日志主题
- $O_{\mathrm{d}}$
- 日志数据
// github.com/ethereum/go-ethereum@v1.10.6/core/vm/instructions.go
// make log instruction function
func makeLog(size int) executionFunc {
return func(pc *uint64, interpreter *EVMInterpreter, scope *ScopeContext) ([]byte, error) {
topics := make([]common.Hash, size)
stack := scope.Stack
mStart, mSize := stack.pop(), stack.pop()
for i := 0; i < size; i++ {
addr := stack.pop()
topics[i] = addr.Bytes32()
}
d := scope.Memory.GetCopy(int64(mStart.Uint64()), int64(mSize.Uint64()))
interpreter.evm.StateDB.AddLog(&types.Log{
Address: scope.Contract.Address(),
Topics: topics,
Data: d,
// This is a non-consensus field, but assigned here because
// core/state doesn't know the current block number.
BlockNumber: interpreter.evm.Context.BlockNumber.Uint64(),
})
return nil, nil
}
}公式 (25)
$$ O{\mathrm{a}} \in \mathbb{B}{20} \quad \wedge \quad \forall x \in O{\mathbf{t}}: x \in \mathbb{B}{32} \quad \wedge \quad O_{\mathbf{d}} \in \mathbb{B} $$
公式 (26)
$M$ 函数
- 定义
- 计算一条日志 $O$ 的摘要函数
- 输入
- ${x \in {O{\mathrm{a}}} \cup O{\mathbf{t}}}$
- 取并集
- 日志地址 $O_{\mathrm{a}}$
- 转成集合 ${O_{\mathrm{a}}}$
- 一系列日志主题
- ${O_{\mathrm{t}}}$
- 输出
- 256字节的哈希
$$ M(O) \quad\equiv\quad {\bigvee}{x \in {O{\mathrm{a}}} \cup O{\mathbf{t}}} \big( M{3:2048}(x) \big) $$
理解如下
$M_{3:2048}$ 是个大小为256字节,共2048位的 Bloom 过滤器
- 对于输入数据,计算它的 Keccak-256 哈希值
- 取哈希值的前6个字节,两两组成一对
- 一对字节有16个比特
- 一共有3对
- 遍历这3对字节
- 取低11位,得到索引,则索引范围是 [0, 2047](2^11 == 2048)
- 设置 Bloom 过滤器对应索引的位为1
- 因此
- 对于输入数据,会设置过滤器的随机3位
公式 (27) (28) (29) (30)
$$ \begin{aligned} M{3:2048}(\mathbf{x}: \mathbf{x} \in \mathbb{B}) & \quad\equiv\quad \mathbf{y}: \mathbf{y} \in \mathbb{B}{256} \quad \text{where:} \ \mathbf{y} & \quad=\quad (0, 0, ..., 0) \quad \text{except:} \ \forall i \in {0, 2, 4} & \quad:\quad \mathcal{B}_{m(\mathbf{x}, i)}(\mathbf{y}) = 1 \ m(\mathbf{x}, i) & \quad\equiv\quad \mathtt{KEC}(\mathbf{x})[i, i + 1] \bmod 2048 \end{aligned} $$
其中
- $\mathcal{B}$ 表示位引用函数
- $\mathcal{B}_{\mathrm{j}}(\mathbf{x}) = 1$ 表示设置字节数组 $\mathbf{x}$ 中的第 j 位(从0开始) 为1
如果仅看黄皮书中关于几个 LOG$ 的 opcode 说明,会误以为过滤器仅包含日志,容易对使用场景产生困惑。实际上,在 go-ethereum 实现中,会把产生日志的合约地址 log.Address 也记录在过滤器
// github.com/ethereum/go-ethereum@v1.10.6/core/types/bloom9.go
// CreateBloom creates a bloom filter out of the give Receipts (+Logs)
func CreateBloom(receipts Receipts) Bloom {
buf := make([]byte, 6)
var bin Bloom
for _, receipt := range receipts {
for _, log := range receipt.Logs {
bin.add(log.Address.Bytes(), buf)
for _, b := range log.Topics {
bin.add(b[:], buf)
}
}
}
return bin
}4.3.2 Holistic Validity 整体有效性
公式 (31)
$$ \begin{aligned} H_{\mathrm{r}} & \quad\equiv\quad \mathtt{TRIE}(LS(\Pi(\boldsymbol{\sigma}, B))) & \quad\quad\wedge \ H{\mathrm{o}} & \quad\equiv\quad \mathtt{KEC}(\mathtt{RLP}(LH^*(B{\mathbf{U}}))) & \quad\quad\wedge \ H{\mathrm{t}} & \quad\equiv\quad \mathtt{TRIE}({\forall i < \lVert B{\mathbf{T}} \rVert, i \in \mathbb{N}: p (i, L{\mathrm{T}}(B{\mathbf{T}}[i]))}) & \quad\quad\wedge \ H{\mathrm{e}} & \quad\equiv\quad \mathtt{TRIE}({\forall i < \lVert B{\mathbf{R}} \rVert, i \in \mathbb{N}: p(i, B{\mathbf{R}}[i])}) & \quad\quad\wedge \ H{\mathrm{b}} & \quad\equiv\quad {\bigvee}{\mathbf{r} \in B{\mathbf{R}}} \big( \mathbf{r}_{\mathrm{b}} \big) \end{aligned} $$
其中
- $H_{\mathrm{r}}$
- storageRoot
- $H_{\mathrm{o}}$
- ommersHash
- $H_{\mathrm{t}}$
- transactionsRoot
- $H_{\mathrm{e}}$
- receiptsRoot
- $H_{\mathrm{b}}$
- logsBloom
其中 公式 (32)
$$ p(k, v) \quad\equiv\quad \big( \mathtt{RLP}(k), \mathtt{RLP}(v) \big) $$
而且 公式 (33)
$$ \mathtt{TRIE}(L_{\mathrm{S}}(\boldsymbol{\sigma})) \quad=\quad {P(B_H)H}{\mathrm{r}} $$
其中
- $P(B_H)$
- 表示区块 B 的父区块
- $\Pi(\boldsymbol{\sigma}, B))$
- 参考公式 (4)
- 参考公式 (177)
- $L_S$
- 世界状态坍塌函数
- 参考公式 (10)
- $L_{\mathrm{H}}^*$
- 参考公式 (34)和(36))
- $L_{\mathrm{T}}$
- 参考公式 (16)
4.3.3 Serialization 序列化
公式 (34) 定义 H 的序列化函数 $L_{\mathrm{H}}$ 如下
$$ L{\mathrm{H}}(H) \quad\equiv\quad (H{\mathrm{p}}, H{\mathrm{o}}, H{\mathrm{c}}, H{\mathrm{r}}, H{\mathrm{t}}, H{\mathrm{e}}, H{\mathrm{b}}, H{\mathrm{d}}, H{\mathrm{i}}, H{\mathrm{l}}, H{\mathrm{g}}, H{\mathrm{s}}, H{\mathrm{x}}, H{\mathrm{m}}, H{\mathrm{n}} \; ) $$
公式 (35) 则 B 的序列化函数 $L_{\mathrm{B}}$ 为
$$ L{\mathrm{B}}(B) \quad\equiv\quad \big( L{\mathrm{H}}(B{\mathrm{H}}), L{\mathrm{T}}^(B{\mathbf{T}}), L{\mathrm{H}}^({B_{\mathbf{U}}}) \big) $$
公式 (36)
其中
- $L_{\mathrm{T}}$ 参考公式 (16)
- $L_{\mathrm{H}}$ 参考公式 (34)
$L{\mathrm{T}}^*$ 和 $L{\mathrm{H}}^*$ 分别是它们的 reduce 函数
reduce 函数定义如下: 对集合中的每一个元素,分别执行指定函数,得到的结果组成一个集合
$$ {f^*}\big( (x_0, x_1, ...) \big) \quad\equiv\quad \big( f(x_0), f(x_1), ... \big) \quad \text{for any function} \; f $$
公式 (37) 值域/约束
$$ \begin{aligned} & {H{\mathrm{p}}} \in \mathbb{B}{32} & \quad\wedge\quad & H{\mathrm{o}} \in \mathbb{B}{32} & \quad\wedge\quad & H{\mathrm{c}} \in \mathbb{B}{20} & \quad\wedge\quad \ & {H{\mathrm{r}}} \in \mathbb{B}{32} & \quad\wedge\quad & H{\mathrm{t}} \in \mathbb{B}{32} & \quad\wedge\quad & {H{\mathrm{e}}} \in \mathbb{B}{32} & \quad\wedge\quad \ & {H{\mathrm{b}}} \in \mathbb{B}{256} & \quad\wedge\quad & H{\mathrm{d}} \in \mathbb{N} & \quad\wedge\quad & {H{\mathrm{i}}} \in \mathbb{N} & \quad\wedge\quad \ & {H{\mathrm{l}}} \in \mathbb{N} & \quad\wedge\quad & H{\mathrm{g}} \in \mathbb{N} & \quad\wedge\quad & {H{\mathrm{s}}} \in \mathbb{N}{256} & \quad\wedge\quad \ & {H{\mathrm{x}}} \in \mathbb{B} & \quad\wedge\quad & H{\mathrm{m}} \in \mathbb{B}{32} & \quad\wedge\quad & {H{\mathrm{n}}} \in \mathbb{B}_{8} \end{aligned} $$
公式 (38)
$$ \mathbb{B}_{\mathrm{n}} = { B: B \in \mathbb{B} \wedge \lVert B \rVert = n } $$
4.3.4 Block Header Validity 区块头验证
公式 (39) 根据区块头 H 找到其父区块
$$ P(H) \equiv B': \mathtt{KEC}(\mathtt{RLP}(B'{\mathrm{H}})) = H{\mathrm{p}} $$
公式 (40) 区块头 H 中的区块编号(block number)计算方式为
$$ H{\mathrm{i}} \equiv {{P(H){\mathrm{H}}}_{\mathrm{i}}} + 1 $$
公式 (41) 根据区块头 H 计算权威难度值的公式
$$ D(H) \equiv \begin{dcases} {D0} & \text{if} \quad H{\mathrm{i}} = 0\ \text{max}!\left({D0}, {P(H){\mathrm{H}}}_{\mathrm{d}} + x\times\varsigma_2 + \epsilon \right) & \text{otherwise}\ \end{dcases} $$
其中
- ${P(H){\mathrm{H}}}{\mathrm{d}}$
- 以父块难度作为难度调整基数
- $x\times\varsigma_2$
- 用于自适应难度调整,维持稳定的出块速度
- $\epsilon$
- 表示设定的难度炸弹
--
// github.com/ethereum/go-ethereum@v1.10.6/consensus/ethash/consensus.go
func makeDifficultyCalculator(bombDelay *big.Int) func(time uint64, parent *types.Header) *big.Int;
// github.com/ethereum/go-ethereum@v1.10.6/consensus/ethash/difficulty.go
func MakeDifficultyCalculatorU256(bombDelay *big.Int) func(time uint64, parent *types.Header) *big.Int;注意两个函数,黄皮书与具体实现存在出入,主要是在 $\epsilon$ 的处理上与公式 (41) 不同,实现为
$$ D(H) \equiv \begin{dcases} {D0} & \text{if} \quad H{\mathrm{i}} = 0\ \text{max}!\left({D0}, {P(H){\mathrm{H}}}_{\mathrm{d}} + x\times\varsigma_2 \right) + \epsilon & \text{otherwise}\ \end{dcases} $$
公式 (42) 创世区块的难度值
$$ {D_0} \equiv 131072 $$
$2^{17} = 131072$
公式 (43) 难度值调整的单位
$$ x \equiv \left\lfloor\frac{{P(H){\mathrm{H}}}{\mathrm{d}}}{2048}\right\rfloor $$
公式 (44) 难度值调整的系数
$$ \varsigma2 \equiv \text{max}\left(y - \left\lfloor\frac{H{\mathrm{s}} - {P(H){\mathrm{H}}}{\mathrm{s}}}{9}\right\rfloor, -99 \right) $$
$$ y \equiv \begin{cases} 1 & \text{if} \, \lVert P(H)_{\mathbf{U}}\rVert = 0 \ 2 & \text{otherwise} \end{cases} $$
其中
- $y$
- 如果父区块中包含叔父块,则难度调整会大一个单位 (从1调整为2)
- 因为包含叔父块时发行的货币量大,需要适当提高难度以保持货币发行量稳定
- $-99$
- 难度一次最多调整 $-99$ 个单位
- 主要是应对被黑客攻击或其他目前想不到的黑天鹅事件
- $y - \left\lfloor\frac{H{\mathrm{s}} - {P(H){\mathrm{H}}}_{\mathrm{s}}}{9}\right\rfloor$
- ${H_{\mathrm{s}}}$
- 本区块的时间戳,以秒为单位
- ${P(H){\mathrm{H}}}{\mathrm{s}}$
- 父区块的时间戳,以秒为单位
- 规定
- ${H{\mathrm{s}}} \gt {P(H){\mathrm{H}}}_{\mathrm{s}}$
- 自适应调整
- 出块时间过短则调大难度
- 出块时间过长则调小难度
- 例子
- 出块时间在 [1,8] 之间
- 出块时间过短
- 难度调大一个单位
- 出块时间在 [9,17] 之间
- 出块时间可以接受
- 难度保持不便
- 出块时间在 [18,26] 之间
- 出块时间过长
- 难度调小一个单位
- ...
公式 (45) (46) (47) 难度炸弹
$$ \epsilon \equiv \left\lfloor 2^{ \left\lfloor H'_{\mathrm{i}} \div 100000 \right\rfloor - 2 } \right\rfloor \ $$
其中
$$ H'{\mathrm{i}} \equiv \max(H{\mathrm{i}} - \kappa, 0) \ $$
其中
$$ \kappa \equiv \begin{cases} 3000000 & \text{if} \quad F{\mathrm{Byzantium}} \leqslant H{\mathrm{i}} < F{\mathrm{Constantinople}} \ 5000000 & \text{if} \quad F{\mathrm{Constantinople}} \leqslant H{\mathrm{i}} < F{\mathrm{Muir Glacier}} \ 9000000 & \text{if} \quad H{\mathrm{i}} \geqslant F{\mathrm{Muir Glacier}} \ \end{cases} $$
$$ \begin{aligned} F{\mathrm{Homestead}} & \equiv 1150000 \ F{\mathrm{Byzantium}} & \equiv 4370000 \ F\mathrm{Constantinople} & \equiv 7280000 \ F{\mathrm{Muir Glacier}} & \equiv 9200000 \end{aligned} $$
为什么设置难度炸弹?
- 降低迁移到 PoS 协议时发生 fork 的风险
- 到时挖矿难度非常大,矿工将被迫迁移到 PoS 协议
参数
- $\epsilon$
- 是2的指数函数,每十万个块扩大一倍
- 后期增长非常快 ("炸弹")
- $H'_{\mathrm{i}}$
- 低估了 PoS 协议的开发难度,导致一再延迟
- 炸弹威力显现后,通过假区块号(回退区块号)来降低难度
- 同时把区块奖励从5个 ETH 降为3个 ETH
参考 what-is-the-difficulty-bomb
公式 (48) gasLimit 约束
$$ H{\mathrm{l}} < {P(H){\mathrm{H}}}{\mathrm{l}} + \left\lfloor\frac{{P(H){\mathrm{H}}}{\mathrm{l}}}{1024}\right\rfloor \quad \wedge \ H{\mathrm{l}} > {P(H){\mathrm{H}}}{\mathrm{l}} - \left\lfloor\frac{{P(H){\mathrm{H}}}{\mathrm{l}}}{1024}\right\rfloor \quad \wedge \ H_{\mathrm{l}} \geqslant 5000 $$
公式 (49) timestamp 约束
$$ H{\mathrm{s}} > {P(H){\mathrm{H}}}_{\mathrm{s}} $$
公式 (41)难度计算公式的设计,保证了难度根据出块间隔长短的动态平衡
- 如果最近的两个区块间隔较短,则会导致难度值增加,因此需要额外的计算量,大概率会延长下个区块的出块时间
- 相反,如果最近的两个区块间隔过长,难度值和下一个区块的预期出块时间也会减少
公式 (50) nonce / mixHash 约束
必须同时满足
$$ n \leqslant \frac {2^{256}}{H{\mathrm{d}}} \quad \wedge \quad m = H{\mathrm{m}} \ with \quad (n, m) = \mathtt{PoW}(H{\cancel{n}}, H{\mathrm{n}}, \mathbf{d}) $$
其中
- $H_{\cancel{n}}$
- 当前区块 header $H$
- 但不包含 nonce 和 mixHash components
- $\mathbf{d}$
- 当前 DAG
- 用于计算 mixHash $H_{\mathrm{m}}$
- $\mathtt{PoW}$
- 工作量证明函数
- 保证 除了列举所有的可能性,没有更好的其他方法来找到一个低于要求阈值的 nonce 攻击者必须拥有超过网络一半的算力,才能比其他人更快地找到 nonce
公式 (51)
综上所述,block header 的验证函数 $V(H)$ 定义如下:
$$ \begin{aligned} V(H) \equiv\quad & n \leqslant \frac{2^{256}}{H{\mathrm{d}}} \wedge m = H{\mathrm{m}} \quad &\wedge \ & H{\mathrm{d}} = D(H) \quad &\wedge \ & H{\mathrm{g}} \le H{\mathrm{l}} \quad &\wedge \ & H{\mathrm{l}} < {P(H){\mathrm{H}}}{\mathrm{l}} + \left\lfloor\frac{{P(H){\mathrm{H}}}{\mathrm{l}}}{1024}\right\rfloor \quad &\wedge \ & H{\mathrm{l}} > {P(H){\mathrm{H}}}{\mathrm{l}} - \left\lfloor\frac{{P(H){\mathrm{H}}}{\mathrm{l}}}{1024}\right\rfloor \quad &\wedge \ & H{\mathrm{l}} \geqslant 5000 \quad &\wedge \ & H{\mathrm{s}} > {P(H){\mathrm{H}}}{\mathrm{s}} \quad &\wedge \ & H{\mathrm{i}} = {P(H){\mathrm{H}}}{\mathrm{i}} +1 \quad &\wedge \ & \lVert H{\mathrm{x}} \rVert \le 32 \ where \quad & (n, m) = \mathtt{PoW}(H{\cancel{n}}, H_{\mathrm{n}}, \mathbf{d}) \end{aligned} $$
此外,$\textbf{extraData}$ 最多为32字节
5. Gas and Payment Gas 与支付
一般来说,用于支付交易的 gas 费用,会被发往 beneficiary 地址,这个地址由矿工设置
6. Transaction Execution 交易执行
$\Upsilon$ 交易状态转换函数
$\Upsilon$ 在执行前,检查如下条件:
- 交易以 RLP 格式正确编码,且没有尾随多余的数据
- 交易签名正确
- nonce 有效(即等于交易发送者账户当前的 nonce)
- gas limit 不小于 $g_0$ (计算公式参考(55) (56) (57))
- 发送者账户 balance 不小于实际费用 $v_0$ (计算公式参考(58))
公式 (52) 交易状态转换函数
$$ \boldsymbol{\sigma}' = \Upsilon(\boldsymbol{\sigma}, T) $$
其中
- $\boldsymbol{\sigma}'$
- 交易完成后的世界状态
- $\Upsilon^{\mathrm{g}}$
- 交易实际消耗的 gas
- $\Upsilon^{\mathbf{l}}$
- 交易执行时产生的一系列日志
- $\Upsilon^{\mathrm{z}}$
- 交易返回的状态码
6.1 Substrate 子状态
公式 (53) 交易执行过程中产生的子状态
$$ A \equiv (A{\mathbf{s}}, A{\mathbf{l}}, A{\mathbf{t}}, A{\mathrm{r}}) $$
其中
- $A_{\mathbf{s}}$
- 自毁集合
- 交易执行完成后会被销毁的账户
- $A_{\mathbf{l}}$
- 一系列日志
- 方便外界旁观者简单跟踪合约调用
- $A_{\mathbf{t}}$
- 交易接触的账户
- 其中的 EMPTY 账户会被删除
- $A_{\mathbf{r}}$
- refund balance
- 累计需要归还的 gas
公式 (54) 空的交易子状态
$$ A^0 \equiv (\varnothing,(), \varnothing, 0) $$
6.2 Execution 执行
状态转换
- $\boldsymbol{\sigma}$ 原始状态
- $\boldsymbol{\sigma}_0$ 检查点状态
- 发送者 balance 扣除 ${T_g}{T_p}$
- 发送者 nonce 累加
- $\boldsymbol{\sigma}_{\mathrm{P}}$ 执行交易后临时状态
- \//
- $\boldsymbol{\sigma}^*$ 预备最终状态
- 剩余的 gas 返回给发送者
- 消耗的 gas 发给 beneficiary(由打包区块的矿工指定)
- $\boldsymbol{\sigma}'$ 最终状态
- 删除自毁集合账户
- 删除接触账户集合中的空账户
--
公式 (55) (56) (57) $g_0$ 交易执行前预付的基础 gas
$$ g0 \equiv {} \sum{i \in T{\mathbf{i}}, T{\mathbf{d}}} \begin{cases} G{\mathrm{txdatazero}} &\text{if} \quad i = 0 \ G{\mathrm{txdatanonzero}} &\text{otherwise} \end{cases} \quad + \quad \begin{cases} G{\mathrm{txcreate}} & \text{if} \quad T{\mathrm{t}} = \varnothing \ 0 & \text{otherwise} \end{cases} \quad + \quad G_{\mathrm{transaction}} $$
其中
- $T_{\mathbf{i}}$
- 合约创建的 initcode
- $T_{\mathbf{d}}$
- 消息调用的 inputdata
- $G_{\mathrm{txcreate}}$
- 如果是合约创建,需要计入成本
公式 (58) $v_0$ 交易执行前预付的费用
$$ v0 \quad\equiv\quad T{\mathrm{g}} T{\mathrm{p}} + T{\mathrm{v}} $$
公式 (59)
$$ \begin{aligned} S(T) & \quad\neq\quad \varnothing \quad \wedge \ \boldsymbol{\sigma}[S(T)] & \quad\neq\quad \varnothing \quad \wedge \ T{\mathrm{n}} & \quad=\quad \boldsymbol{\sigma}[S(T)]{\mathrm{n}} \quad \wedge \ g0 & \quad\leqslant\quad T{\mathrm{g}} \quad \wedge \ v0 & \quad\leqslant\quad \boldsymbol{\sigma}[S(T)]{\mathrm{b}} \quad \wedge \ T{\mathrm{g}} & \quad\leqslant\quad {B{\mathrm{H}}}{\mathrm{l}} - {\ell}(B{\mathbf{R}})_{\mathrm{u}} \end{aligned} $$
其中
- $S(T)$
- 根据交易查找其发送者的函数
- $T_{\mathrm{g}}$
- 交易的 gasLImit
- ${\ell}(B{\mathbf{R}}){\mathrm{u}}$
- 当前区块累计已经消耗的 gas
- ${B{\mathrm{H}}}{\mathrm{l}}$
- 当前区块的 gasLimit
公式 (60) (61) (62) 检查点状态 $\boldsymbol{\sigma}_0$
$$ \begin{aligned} \boldsymbol{\sigma}_0 & \quad\equiv\quad \boldsymbol{\sigma} \quad \text{except:} \ \boldsymbol{\sigma}0[S(T)]{\mathrm{b}} & \quad\equiv\quad \boldsymbol{\sigma}[S(T)]{\mathrm{b}} - T{\mathrm{g}} T_{\mathrm{p}} \ \boldsymbol{\sigma}0[S(T)]{\mathrm{n}} & \quad\equiv\quad \boldsymbol{\sigma}[S(T)]_{\mathrm{n}} + 1 \end{aligned} $$
检查点状态 $\boldsymbol{\sigma}0$ 预扣了 $T{\mathrm{g}} T_{\mathrm{p}}$
系统会在交易执行成功后,将剩余 gas 返还发送者
--
注意 XXX
公式 (61) 计算检查点状态 balance 时,不是扣除 $v0$,而是只扣了 $T{\mathrm{g}} T{\mathrm{p}}$,未扣除 $T{\mathrm{v}}$
实际上,$v$ 的处理,是在公式 (63) 执行交易时,在执行具体函数代码前,会从发送者 Transfer 到接收者
gas 与 value 分开处理,理解如下
- gas 本身与 value 语义本质量不同,不能混为一起
- 转账 value 的双方 balance 的改变应该是原子的,不应拆成前后两个上下文
- gas 一定是外部账户支付的,而 value 转账的扣款账户可以是外部账户,也可以是智能合约
// github.com/ethereum/go-ethereum@v1.10.6/core/vm/evm.go
// Call executes the contract associated with the addr with the given input as
// parameters. It also handles any necessary value transfer required and takes
// the necessary steps to create accounts and reverses the state in case of an
// execution error or failed value transfer.
func (evm *EVM) Call(caller ContractRef, addr common.Address, input []byte, gas uint64, value *big.Int) (ret []byte, leftOverGas uint64, err error) {
evm.Context.Transfer(evm.StateDB, caller.Address(), addr, value)
//...
}公式 (63) 执行交易后临时状态 $\boldsymbol{\sigma}_{\mathrm{P}}$
$$ (\boldsymbol{\sigma}{\mathrm{P}}, g', A, z) \equiv \begin{cases} \Lambda{4}(\boldsymbol{\sigma}0, S(T), T{\mathrm{o}}, g, T{\mathrm{p}}, T{\mathrm{v}}, T{\mathbf{i}}, 0, \varnothing, \top) & \text{if} \quad T{\mathrm{t}} = \varnothing \ \Theta_{4}(\boldsymbol{\sigma}0, S(T), T{\mathrm{o}}, T{\mathrm{t}}, T{\mathrm{t}}, g, T{\mathrm{p}}, T{\mathrm{v}}, T{\mathrm{v}}, T{\mathbf{d}}, 0, \top) & \text{otherwise} \end{cases} $$
状态转换
- $\boldsymbol{\sigma}_0$ 检查点状态
- $\boldsymbol{\sigma}_{\mathrm{P}}$ 执行交易后临时状态 操作
- 转换时需要区分交易类型
- $T_{\mathrm{t}} = \varnothing$ 未设置目标地址,说明是合约创建类型
- 否则,是消息调用类型
其中
- $\boldsymbol{\sigma}_{\mathrm{P}}$
- 交易执行后的临时状态
- $g'$
- 剩余 gas
- $A$
- 子状态
- $z$
- 状态码
- $T_{\mathrm{o}}$
- original transactor
- 如果是 inner-transaction,则这里是智能合约的地址,而非 sender
- $\Lambda_{4}$
- 合约创建
- 参考 合约创建
- $\Theta_{4}$
- 消息调用
- 参考 消息调用
- $\top$
- 数学符号,表示 bool 值
- $\Lambda{4}$ 和 $\Theta{4}$ 的末尾参数
- 含义:是否有权修改状态
--
关于 $\top$
| OPCODE | 函数 | 末尾参数值 | 含义 |
|---|---|---|---|
CREATE |
$\Lambda_{4}$ | $I_{w}$ | 保持调用时的读写权限 |
CREATE2 |
$\Lambda_{4}$ | $I_{w}$ | 保持调用时的读写权限 |
STATICCALL |
$\Theta_{4}$ | $\bot$ (falsum) | 只读 |
CALL |
$\Theta_{4}$ | $I_{w}$ | 保持调用时的读写权限 |
CALLCODE |
$\Theta_{4}$ | $I_{w}$ | 保持调用时的读写权限 |
DELEGATECALL |
$\Theta_{4}$ | $I_{w}$ | 保持调用时的读写权限 |
// github.com/ethereum/go-ethereum@v1.10.6/core/vm/interpreter.go
func (in *EVMInterpreter) Run(contract *Contract, input []byte, readOnly bool) (ret []byte, err error) {
// ...
// Make sure the readOnly is only set if we aren't in readOnly yet.
// This also makes sure that the readOnly flag isn't removed for child calls.
if readOnly && !in.readOnly {
in.readOnly = true
defer func() { in.readOnly = false }()
}
// ...
for {
// ...
op = contract.GetOp(pc)
operation := in.cfg.JumpTable[op]
// If the operation is valid, enforce write restrictions
if in.readOnly && in.evm.chainRules.IsByzantium {
// If the interpreter is operating in readonly mode, make sure no
// state-modifying operation is performed. The 3rd stack item
// for a call operation is the value. Transferring value from one
// account to the others means the state is modified and should also
// return with an error.
if operation.writes || (op == CALL && stack.Back(2).Sign() != 0) {
return nil, ErrWriteProtection
}
}
// ...
}
return nil, nil
}
//
// github.com/ethereum/go-ethereum@v1.10.6/core/vm/evm.go
// StaticCall executes the contract associated with the addr with the given input
// as parameters while disallowing any modifications to the state during the call.
// Opcodes that attempt to perform such modifications will result in exceptions
// instead of performing the modifications.
func (evm *EVM) StaticCall(caller ContractRef, addr common.Address, input []byte, gas uint64) (ret []byte, leftOverGas uint64, err error) {
// ...
ret, err = evm.interpreter.Run(contract, input, true)
// ...
}
func (evm *EVM) Call(caller ContractRef, addr common.Address, input []byte, gas uint64, value *big.Int) (ret []byte, leftOverGas uint64, err error) {
// ...
ret, err = evm.interpreter.Run(contract, input, false)
// ...
}
func (evm *EVM) CallCode(caller ContractRef, addr common.Address, input []byte, gas uint64, value *big.Int) (ret []byte, leftOverGas uint64, err error) {
// ...
ret, err = evm.interpreter.Run(contract, input, false)
// ...
}
func (evm *EVM) DelegateCall(caller ContractRef, addr common.Address, input []byte, gas uint64) (ret []byte, leftOverGas uint64, err error) {
// ...
ret, err = evm.interpreter.Run(contract, input, false)
// ...
}
func (evm *EVM) create(caller ContractRef, codeAndHash *codeAndHash, gas uint64, value *big.Int, address common.Address) ([]byte, common.Address, uint64, error) {
// ...
ret, err = evm.interpreter.Run(contract, nil, false)
// ...
}--
公式 (64) 执行时最多能消耗的 gas
$$ g \quad\equiv\quad T_{\mathrm{g}} - g_0 $$
公式 (65) 交易执行后 refund 计数器的变化
$$ A'{\mathrm{r}} \quad\equiv\quad A{\mathrm{r}} + \sum{i \in A{\mathbf{s}}} R_{\mathrm{selfdestruct}} $$
公式 (66) 交易执行后剩余的 gas
$$ g^* \quad\equiv\quad g' + \min \left{ \Big\lfloor \dfrac{T{\mathrm{g}} - g'}{2} \Big\rfloor, {A'{\mathrm{r}}} \right} $$
其中
- $g'$
- 交易执行后最终剩余的 gas
- $T_{\mathrm{g}} - g'$
- 交易实际消耗的 gas
- $g^*$
- 交易执行后最终需要返还的 gas
公式 (67) (68) (69) (70) 预备最终状态 $\boldsymbol{\sigma}^*$
$$ \begin{aligned} \boldsymbol{\sigma}^ & \quad\equiv\quad \boldsymbol{\sigma}_{\mathrm{P}} \quad \text{except} \ \boldsymbol{\sigma}^[S(T)]{\mathrm{b}} & \quad\equiv\quad \boldsymbol{\sigma}{\mathrm{P}}[S(T)]{\mathrm{b}} + g^* T{\mathrm{p}} \ \boldsymbol{\sigma}^[m]{\mathrm{b}} & \quad\equiv\quad \boldsymbol{\sigma}{\mathrm{P}}[m]{\mathrm{b}} + (T{\mathrm{g}} - g^) T{\mathrm{p}} \ m & \quad\equiv\quad {B{\mathrm{H}}}_{\mathrm{c}} \end{aligned} $$
状态转换
- $\boldsymbol{\sigma}_{\mathrm{P}}$ 执行交易后临时状态
- $\boldsymbol{\sigma}^*$ 预备最终状态 操作
- 剩余的 gas 返回给发送者
- 消耗的 gas 发给 ${B{\mathrm{H}}}{\mathrm{c}}$ (beneficiary)
公式 (71) (72) (73) 最终状态 $\boldsymbol{\sigma}'$
$$ \begin{aligned} \boldsymbol{\sigma}' & \quad\equiv\quad \boldsymbol{\sigma}^ \quad \text{except} \ \forall i \in A{\mathbf{s}}: \boldsymbol{\sigma}'[i] & \quad=\quad \varnothing \ \forall i \in A{\mathbf{t}}: \boldsymbol{\sigma}'[i] & \quad=\quad \varnothing \quad\text{if}\quad \mathtt{DEAD}(\boldsymbol{\sigma}^\kern -2pt, i) \end{aligned} $$
状态转换
- $\boldsymbol{\sigma}^*$ 预备最终状态
- $\boldsymbol{\sigma}'$ 最终状态 操作
- 删除自毁集合账户
- 删除接触账户集合中的空账户
公式 (74) (75) (76)
$$ \begin{aligned} \Upsilon^{\mathrm{g}}(\boldsymbol{\sigma}, T) & \quad\equiv\quad T{\mathrm{g}} - g^* \ \Upsilon^{\mathbf{l}}(\boldsymbol{\sigma}, T) & \quad\equiv\quad {A{\mathbf{l}}} \ \Upsilon^{\mathrm{z}}(\boldsymbol{\sigma}, T) & \quad\equiv\quad z \end{aligned} $$
其中
- $\Upsilon^{\mathrm{g}}$
- 交易一共消耗的 gas
- $\Upsilon^\mathbf{l}$
- 交易生成的一系列日志
- $\Upsilon^{\mathrm{z}}$
- 交易执行返回的状态码
7. Contract Creation 合约创建
两个步骤
- 合约创建
- 合约初始化
- 调用 $\mathbf{i}$
公式 (77) 盐
$$ \zeta \in \mathbb{B}{32} \cup \mathbb{B}{0} $$
如果是通过 $\small{CREATE2}$ 创建合约,则 $\zeta \neq \varnothing$
公式 (78) 合约创建函数 $\Lambda$
$$ (\boldsymbol{\sigma}', g', A, z, \mathbf{o}) \equiv \Lambda(\boldsymbol{\sigma}, s, o, g, p, v, \mathbf{i}, e, \zeta, w) $$
函数参数
- $\boldsymbol{\sigma}$
- 世界状态
- $s$
- 发送者 sender
- $o$
- 调用者 original transactor
- $g$
- available gas
- $p$
- gas price
- $v$
- 捐献: endowment
- $\mathbf{i}$
- 用于初始化合约的 EVM 代码(二进制字符串)
- $e$
- 当前消息调用/合约创建堆栈的深度
- $\zeta$
- 用于计算新合约地址的盐
- 可能不存在: $\zeta = \varnothing$
- $w$
- 是否有权改变状态
- 参考公式 (63)
函数输出
- $\boldsymbol{\sigma}'$
- 世界状态'
- $g'$
- 剩余 gas
- $A$
- 子状态
- 参考 #6.1 Substrate
- $\mathbf{o}$
- 执行结果
- 对于合约创建而言,成功的话这里得到的是合约的 body code
- 参考公式 (145)
公式 (79) (80) (81) 新创建合约的地址 $a$
$$ \begin{aligned} a & \equiv \mathtt{ADDR}(s, \boldsymbol{\sigma}[s]{\mathrm{n}} - 1, \zeta, \mathbf{i}) \ \mathtt{ADDR}(s, n, \zeta, \mathbf{i}) & \equiv \mathcal{B}{96..255}\Big(\mathtt{KEC}\big( L{\mathrm{A}}(s, n, \zeta, \mathbf{i})\big) \Big) \ L{\mathrm{A}}(s, n, \zeta, \mathbf{i}) & \equiv \begin{cases} \mathtt{RLP}\big(\;(s, n)\;\big) & \text{if}\ \zeta = \varnothing \ (255) \cdot s \cdot \zeta \cdot \mathtt{KEC}(\mathbf{i}) & \text{otherwise} \end{cases} \end{aligned} $$
其中
- $L_{\mathrm{A}}$
- 判断合约创建方式是否为 $\small{CREATE2}$
- $\cdot$
- 拼接字节数组
- $\mathcal{B}_{a..b}(X)$
- 取二进制字节数组的第 $[a, b]$ 位
- $\boldsymbol{\sigma}[x]$
- 地址 $x$ 的世界状态
- 不存在,则为 $\varnothing$
注意
- 公式(79) 中,传给合约地址计算函数 $\Lambda$ 的参数 nonce,值是 $\boldsymbol{\sigma}[s]_{\mathrm{n}} - 1$
- 理解: 在调用合约创建之前,系统已经把发送者的 nonce 加一
公式 (82) (83) (84) (85) 合约创建后的世界状态 $\boldsymbol{\sigma}^*$
$$ \begin{aligned} \boldsymbol{\sigma}^ & \quad\equiv\quad \boldsymbol{\sigma} \quad \text{except:} \ \boldsymbol{\sigma}^[a] & \quad=\quad \big( 1, v + v', \mathtt{TRIE}(\varnothing), \mathtt{KEC}\big(()\big) \big) \ \boldsymbol{\sigma}^[s] & \quad=\quad \begin{cases} \varnothing & \text{if}\ \boldsymbol{\sigma}[s] = \varnothing \ \wedge\ v = 0 \ \mathbf{a}^ & \text{otherwise} \end{cases} \ \mathbf{a}^* & \quad\equiv\quad (\boldsymbol{\sigma}[s]{\mathrm{n}}, \boldsymbol{\sigma}[s]{\mathrm{b}} - v, \boldsymbol{\sigma}[s]{\mathbf{s}}, \boldsymbol{\sigma}[s]{\mathrm{c}}) \end{aligned} $$
公式 (86) $v'$ 合约地址在交易前就有的余额
$$ v' \equiv \begin{cases} 0 & \text{if} \quad \boldsymbol{\sigma}[a] = \varnothing\ \boldsymbol{\sigma}[a]_{\mathrm{b}} & \text{otherwise} \end{cases} $$
到这里,新创建合约的地址的状态已经设置好了(公式(83))
公式 (87) 调用 $\Xi$ 函数执行代码 $\mathbf{i}$ 来初始化合约
$$ (\boldsymbol{\sigma}^{}, g^{}, A, \mathbf{o}) \quad\equiv\quad \Xi(\boldsymbol{\sigma}^*, g, I, {s, a}) \ $$
$\Xi$ 函数的输出
- $\boldsymbol{\sigma}^{**}$
- 合约初始化后的世界状态
- $g^{**}$
- 剩余的可用 gas
- $A$
- 累积的子状态
- $\mathbf{o}$
- 新创建合约的 body code
- 由合约初始化 $\mathbf{i}$ 代码得到
公式 (88) (89) (90) (91) (92) (93) (94) (95) (96) 合约初始化后的世界状态 $\boldsymbol{\sigma}^*$
$I$ 作为 $\Xi$ 函数的输入参数
- 表示 执行环境的一系列变量
- 参考 #9.3 Execution Environment
$$ \begin{aligned} I{\mathrm{a}} & \quad\equiv\quad a \ I{\mathrm{o}} & \quad\equiv\quad o \ I{\mathrm{p}} & \quad\equiv\quad p \ I{\mathbf{d}} & \quad\equiv\quad () \ I{\mathrm{s}} & \quad\equiv\quad s \ I{\mathrm{v}} & \quad\equiv\quad v \ I{\mathbf{b}} & \quad\equiv\quad \mathbf{i} \ I{\mathrm{e}} & \quad\equiv\quad e \ I_{\mathrm{w}} & \quad\equiv\quad w \end{aligned} $$
- $I_{\mathrm{a}}$
- 新创建合约的地址
- $I_{\mathrm{o}}$
- 调用者 original transactor
- $I_{\mathrm{p}}$
- gas Price
- $I_{\mathbf{d}}$
- input data
- 在这里为空,因为对于这个初始化调用而言没有 input
- $I_{\mathrm{s}}$
- 发送者 sender
- $I_{\mathrm{v}}$
- 捐献: endowment
- $I_{\mathbf{b}}$
- 用于初始化合约的 EVM 代码(二进制字符串)
- $I_{\mathrm{e}}$
- 当前消息调用/合约创建堆栈的深度
- $I_{\mathrm{w}}$
- 是否有权修改状态
- 参考公式 (63)
公式 (97) 合约初始化需要支付的 gas
$$ c \quad\equiv\quad G_{\mathrm{codedeposit}} \times \lVert \mathbf{o} \rVert $$
- 出现异常
- 初始化代码执行过程的异常
- 例子
- 因可用 gas $g^{**}$ 不够而导致 Out-Of-Gas 异常
- 成功初始化后可用 gas 不够支付 $c$
- $g^{**} < c$
- 也会导致 Out-of-Gas
- 其他场景
- 例子 TODO
- 导致
- 最终剩余 gas $g‘$ 为0
- 使初始化提前终止
- 合约初始化后的世界状态 $\boldsymbol{\sigma}^{**}$ 为空,即 $\varnothing$
- 最终状态与合约创建前一致
公式 (98) (99) (100) (101) 最终状态 $\boldsymbol{\sigma}'$
$$ \begin{aligned} \quad g' \quad\equiv\quad & \begin{cases} 0 & \text{if} \quad F \ g^{} - c & \text{otherwise} \ \end{cases} \ \quad \boldsymbol{\sigma}' \quad\equiv\quad & \begin{cases} \boldsymbol{\sigma} & \text{if} \quad F \ \lor\ \boldsymbol{\sigma}^{} = \varnothing \ \boldsymbol{\sigma}^{} \quad \text{except:} & \ \quad\boldsymbol{\sigma}'[a] = \varnothing & \text{if} \quad \mathtt{DEAD}(\boldsymbol{\sigma}^{}, a) \ \boldsymbol{\sigma}^{} \quad \text{except:} & \ \quad\boldsymbol{\sigma}'[a]_{\mathrm{c}} = \texttt{KEC}(\mathbf{o}) & \text{otherwise} \end{cases} \ \quad z \quad\equiv\quad & \begin{cases} 0 & \text{if} \quad F \ \lor\ \boldsymbol{\sigma}^{} = \varnothing \ 1 & \text{otherwise} \end{cases} \ \text{where} \ F \quad\equiv\quad & \big( \boldsymbol{\sigma}[a] \neq \varnothing \ \wedge\ \big(\boldsymbol{\sigma}[a]_c \neq \texttt{\small KEC}\big(()\big) \vee \boldsymbol{\sigma}[a]_n \neq 0 \big) \big) \quad \vee \ &(\boldsymbol{\sigma}^{} = \varnothing \ \wedge\ \mathbf{o} = \varnothing) \quad \vee \ &g^{} < c \quad \vee \ &\lVert \mathbf{o} \rVert > 24576 \end{aligned} $$
其中
- $g'$
- 最终剩余的 gas,需要返还给最初交易发起者
- $\big( \boldsymbol{\sigma}[a] \neq \varnothing \ \wedge\ \big(\boldsymbol{\sigma}[a]_c \neq \texttt{\small KEC}\big(()\big) \vee \boldsymbol{\sigma}[a]_n \neq 0 \big) \big)$
- 目标地址已存在,且有 codeHash 或 nonce 不为0
- $\mathbf{o}$
- 新创建合约的 body code
- 由合约初始化 $\mathbf{i}$ 代码得到
- $\boldsymbol{\sigma}'[a]_{\mathrm{c}} = \texttt{KEC}(\mathbf{o})$
- 保存新建合约的 body code 的 hash 到 $\boldsymbol{\sigma}'[a]_{\mathrm{c}}$
-
$\boldsymbol{\sigma}^{**} = \varnothing \ \wedge\ \mathbf{o} = \varnothing$
-
含义
-
执行 $\mathbf{i}$ 后得到的字节码,即合约代码 $\mathbf{o}$ 为空
-
失败例子 Ropsten
-
$\text{\small SELFDESTRUCT}$
- 结论
- 根据执行结果,剩余 gas 有返还,所以不属于 $F$
- 代码
-
pragma solidity >=0.7.0 <0.9.0;
contract Storage {
constructor(address user) payable {
address payable u = payable(address(user));
selfdestruct(u);
}
}结论
- 要么带着初始捐款(endowment)成功创建合约
- 要么不会创建任何合约且不会进行转账
-
REVERT
// github.com/ethereum/go-ethereum@v1.10.6/core/vm/interpreter.go
// It's important to note that any errors returned by the interpreter should be
// considered a revert-and-consume-all-gas operation except for
// ErrExecutionReverted which means revert-and-keep-gas-left.
func (in *EVMInterpreter) Run(contract *Contract, input []byte, readOnly bool) (ret []byte, err error) {
// ...
}-
测试
- 结论
- 不满足 $F$,因此 $g' = g^{**} - c$
- 剩余 gas 和 value 会被归还
- 满足 $\mathtt{DEAD}(\boldsymbol{\sigma}^{**}, a)$,因此 $\boldsymbol{\sigma}'[a] = \varnothing$
- 其余状态不变
- 证明
- 代码 (assert 和 require 都测试过,都返还了 gas,跟参考文章结论不一样)
pragma solidity >=0.7.0 <0.9.0;
contract Storage {
uint256 number;
constructor(address user, uint256 num) payable {
require (msg.sender == user);
number = num;
}
}- 部署
- 发起部署的地址与构造函数的地址不同,使 require/assert 失败
- 根据公式(14),新创建的合约是个 EMPTY 账户
const targetContract = '0xbd83EF1a5A45b54d94895C1897aF2d00154520D5';
const balance = await web3.eth.getBalance(targetContract);
const nonce = await web3.eth.getTransactionCount(targetContract);
const code = await web3.eth.getCode(targetContract);
console.log(`balance: ${balance}`);
console.log(`nonce: ${nonce}`);
console.log(`code: ${code}`);
// storageRoot
// 无法从 web3 直接获得
// 参考 https://github.com/medvedev1088/ethereum-merkle-patricia-trie-example8. Message Call 消息调用 (internal Transaction)
公式 (102) 消息调用函数 $\Theta$
$$ (\boldsymbol{\sigma}', g', A, z, \mathbf{o}) \equiv {\Theta}(\boldsymbol{\sigma}, s, o, r, c, g, p, v, \tilde{v}, \mathbf{d}, e, w) $$
函数参数
- $\boldsymbol{\sigma}$
- 世界状态
- $s$
- 发送者 sender
- $o$
- 调用者 original transactor
- $r$
- 接收者 recipient
- $c$
- 消息调用执行在哪个地址上的代码,通常等于 $r$
- 参考 Appendix H2. Instruction Set 的 ${\small CALL}$, ${\small CALLCODE}$
- $g$
- available gas
- $p$
- gas price
- $v$
- 捐献: endowment
- $\mathbf{d}$
- 消息调用的 input data (二进制字符串)
- $e$
- 当前消息调用/合约创建堆栈的深度
- $w$
- 是否有权改变状态
- 参考公式 (63)
函数输出
- $\boldsymbol{\sigma}'$
- 世界状态'
- $g'$
- 剩余 gas
- $A$
- 子状态
- 参考 #6.1 Substrate
- $z$
- status code
- $\mathbf{o}$
- output data
- 参考公式 (145)
注意区分
- $v$
- msg.value
- $\tilde{v}$
- ${\small DELEGATECALL}$ 指令上下文的中的 value
公式 (103) 临时状态 $\boldsymbol{\sigma}_1$
$$ \begin{aligned} &\boldsymbol{\sigma}1[r]{\mathrm{b}} \equiv \boldsymbol{\sigma}[r]_{\mathrm{b}} + v \quad\wedge\quad \boldsymbol{\sigma}1[s]{\mathrm{b}} \equiv \boldsymbol{\sigma}[s]_{\mathrm{b}} - v \ & unless s = r \end{aligned} $$
意味着
公式 (104) (105) (106) (107) (108) (109) 状态转换 $\boldsymbol{\sigma}$ -> $\boldsymbol{\sigma}_1'$ -> $\boldsymbol{\sigma}_1$
$$ %\boxed{% \boldsymbol{\sigma}_1 \equiv \boldsymbol{\sigma}_1' \quad \text{except:} %}% $$
$$ \boldsymbol{\sigma}_1[s] \equiv \begin{cases} \varnothing & \text{if}\ \boldsymbol{\sigma}_1'[s] = \varnothing \ \wedge\ v = 0 \ \mathbf{a}_1 &\text{otherwise} \ \end{cases} \ $$
$$ \mathbf{a}_1 \equiv \left(\boldsymbol{\sigma}1'[s]{\mathrm{n}}, \boldsymbol{\sigma}1'[s]{\mathrm{b}} - v, \boldsymbol{\sigma}1'[s]{\mathbf{s}}, \boldsymbol{\sigma}1'[s]{\mathrm{c}}\right) $$
$$ \text{and}\quad \boldsymbol{\sigma}_1' \equiv \boldsymbol{\sigma} \quad \text{except:} $$
$$ \begin{cases} \boldsymbol{\sigma}_1'[r] \equiv (0, v, \mathtt{TRIE}(\varnothing), \mathtt{KEC}(())) & \text{if} \quad \boldsymbol{\sigma}[r] = \varnothing \wedge v \neq 0 \ \boldsymbol{\sigma}_1'[r] \equiv \varnothing & \text{if}\quad \boldsymbol{\sigma}[r] = \varnothing \wedge v = 0 \ \boldsymbol{\sigma}_1'[r] \equiv \mathbf{a}_1' & \text{otherwise} \end{cases} $$
$$ \mathbf{a}1' \equiv (\boldsymbol{\sigma}[r]{\mathrm{n}}, \boldsymbol{\sigma}[r]{\mathrm{b}} + v, \boldsymbol{\sigma}[r]{\mathbf{s}}, \boldsymbol{\sigma}[r]_{\mathrm{c}}) $$
执行过程参考 #9 Execution Model
公式 (110) (111) ... (123) 最终状态 $\boldsymbol{\sigma}'$
$$ \begin{aligned} \boldsymbol{\sigma}' & \quad\equiv\quad \begin{cases} \boldsymbol{\sigma} & \text{if} \quad \boldsymbol{\sigma}^{} = \varnothing \ \boldsymbol{\sigma}^{} & \text{otherwise} \end{cases} \ g' & \quad\equiv\quad \begin{cases} 0 & \text{if} \quad \boldsymbol{\sigma}^{} = \varnothing \ \wedge \mathbf{o} = \varnothing \ g^{} & \text{otherwise} \end{cases} \ z & \quad\equiv\quad \begin{cases} 0 & \text{if} \quad \boldsymbol{\sigma}^{} = \varnothing \ 1 & \text{otherwise} \end{cases} \ (\boldsymbol{\sigma}^{}, g^{**},A, \mathbf{o}) & \quad\equiv\quad \Xi\ I{\mathrm{a}} & \quad\equiv\quad r \ I{\mathrm{o}} & \quad\equiv\quad o \ I{\mathrm{p}} & \quad\equiv\quad p \ I{\mathbf{d}} & \quad\equiv\quad \mathbf{d} \ I{\mathrm{s}} & \quad\equiv\quad s \ I{\mathrm{v}} & \quad\equiv\quad \tilde{v} \ I{\mathrm{e}} & \quad\equiv\quad e \ I{\mathrm{w}} & \quad\equiv\quad w \ \mathbf{t} & \quad\equiv\quad {s, r} \ where \ \end{aligned} \ \Xi \equiv \begin{cases} \Xi_{\mathtt{ECREC}}(\boldsymbol{\sigma}1, g, I, \mathbf{t}) & \text{if} \quad c = 1 \ \Xi{\mathtt{SHA256}}(\boldsymbol{\sigma}1, g, I, \mathbf{t}) & \text{if} \quad c = 2 \ \Xi{\mathtt{RIP160}}(\boldsymbol{\sigma}1, g, I, \mathbf{t}) & \text{if} \quad c = 3 \ \Xi{\mathtt{ID}}(\boldsymbol{\sigma}1, g, I, \mathbf{t}) & \text{if} \quad c = 4 \ \Xi{\mathtt{EXPMOD}}(\boldsymbol{\sigma}1, g, I, \mathbf{t}) & \text{if} \quad c = 5 \ \Xi{\mathtt{BN_ADD}}(\boldsymbol{\sigma}1, g, I, \mathbf{t}) & \text{if} \quad c = 6 \ \Xi{\mathtt{BN_MUL}}(\boldsymbol{\sigma}1, g, I, \mathbf{t}) & \text{if} \quad c = 7 \ \Xi{\mathtt{SNARKV}}(\boldsymbol{\sigma}1, g, I, \mathbf{t}) & \text{if} \quad c = 8 \ \Xi{\mathtt{BLAKE2_F}}(\boldsymbol{\sigma}_1, g, I, \mathbf{t}) & \text{if} \quad c = 9 \ \Xi(\boldsymbol{\sigma}_1, g, I, \mathbf{t}) & \text{otherwise} \end{cases} $$
$$ \text{Let} \; \mathtt{KEC}(I{\mathbf{b}}) = \boldsymbol{\sigma}[c]{\mathrm{c}} $$
其中
- $I_{\mathrm{a}}$
- 接收者地址
- $I_{\mathrm{o}}$
- 调用者 original transactor
- $I_{\mathrm{p}}$
- gas Price
- $I_{\mathbf{d}}$
- 消息调用的 input data (二进制字符串)
- $I_{\mathrm{s}}$
- 发送者 sender
- $I_{\mathrm{v}}$
- $\tilde{v}$
- ${\small DELEGATECALL}$ 指令上下文的中的 value
- $I_{\mathrm{e}}$
- 当前消息调用/合约创建堆栈的深度
- $I_{\mathrm{w}}$
- 是否有权改变状态
- 参考公式 (63)
注意
- 映射
- 客户端会存储映射 $\mathtt{KEC}(I{\mathbf{b}})$ => $I{\mathbf{b}}$
- 这样可以方便根据 $\boldsymbol{\sigma}[c]{\mathrm{c}}$ 索引并取出目标地址的代码 $I{\mathbf{b}}$ 以执行
- 预编译合约
- c 在 [1, 9] 表示预编译合约
- 参考 # Appendix E. Precompiled Contracts
9. Execution Model 执行模型
参考 go-ethereum 源码
// github.com/ethereum/go-ethereum@v1.10.6/core/state_processor.go
func applyTransaction(msg types.Message, config *params.ChainConfig, bc ChainContext, author *common.Address, gp *GasPool, statedb *state.StateDB, blockNumber *big.Int, blockHash common.Hash, tx *types.Transaction, usedGas *uint64, evm *vm.EVM) (*types.Receipt, error);
// github.com/ethereum/go-ethereum@v1.10.6/core/state_transition.go
func ApplyMessage(evm *vm.EVM, msg Message, gp *GasPool) (*ExecutionResult, error);
func (st *StateTransition) TransitionDb() (*ExecutionResult, error);
// github.com/ethereum/go-ethereum@v1.10.6/core/vm/evm.go
func (evm *EVM) Call(caller ContractRef, addr common.Address, input []byte, gas uint64, value *big.Int) (ret []byte, leftOverGas uint64, err error);
// github.com/ethereum/go-ethereum@v1.10.6/core/vm/interpreter.go
func (in *EVMInterpreter) Run(contract *Contract, input []byte, readOnly bool) (ret []byte, err error);
// github.com/ethereum/go-ethereum@v1.10.6/core/vm/jump_table.go
type (
executionFunc func(pc *uint64, interpreter *EVMInterpreter, callContext *ScopeContext) ([]byte, error)
)
type operation struct {
execute executionFunc
}
// github.com/ethereum/go-ethereum@v1.10.6/core/vm/instructions.go9.1 Basics 基础
9.2 Fees Overview 费用概述
- 消耗
- 代码执行
- 进一步的 消息调用 或 合约创建
- 内存使用
- refund
- 如果清除了一块存储,系统会免除这项操作的费用,且返还一定额度的 refund
- 参考 # Appendix G. Fee Schedule
- $R_{\mathrm{sclear}}$
- $R_{\mathrm{selfdestruct}}$
9.3 Execution Environment 执行环境
$I$ 执行环境
组成
- $I_{\mathrm{a}}$
- 接收者地址
- $I_{\mathrm{o}}$
- 调用者 original transactor
- $I_{\mathrm{p}}$
- gas Price
- $I_{\mathbf{d}}$
- 消息调用的 input data (二进制字符串)
- $I_{\mathrm{s}}$
- 发送者 sender
- $I_{\mathrm{v}}$
- value
- $I_{\mathrm{b}}$
- 接收者的代码,将被执行
- $I_{\mathrm{H}}$
- 当前区块的区块头
- $I_{\mathrm{e}}$
- 当前消息调用/合约创建堆栈的深度
- $I_{\mathrm{w}}$
- 是否有权改变状态
- 参考公式 (63)
公式 (124) 函数 $\Xi$
$$ (\boldsymbol{\sigma}', g', A, \mathbf{o}) \equiv \Xi(\boldsymbol{\sigma}, g, I) $$
其中
- $\mathbf{o}$
- 执行结果 output
公式 (125) 累计子状态 $A$
$$ A \equiv (A{\mathbf{s}}, A{\mathbf{l}}, A{\mathbf{t}}, A{\mathrm{r}}) $$
- $A_{\mathbf{s}}$
- 自毁集合
- 交易执行完成后会被销毁的账户
- $A_{\mathbf{l}}$
- 一系列日志
- 方便外界旁观者简单跟踪合约调用
- $A_{\mathbf{t}}$
- 交易接触的账户
- 其中的 EMPTY 账户会被删除
- $A_{\mathbf{r}}$
- refund balance
- 累计需要归还的 gas
9.4 Execution Overview 执行概述
公式 (126) (127) (128) ... (137) (138) 函数 ${\Xi}$ 的定义
$$ \begin{aligned} \Xi(\boldsymbol{\sigma}, g, I, T) & \quad\equiv\quad (\boldsymbol{\sigma}'!, \boldsymbol{\mu}'{\mathrm{g}}, A, \mathbf{o}) \ (\boldsymbol{\sigma}', \boldsymbol{\mu}'!, A, ..., \mathbf{o}) & \quad\equiv\quad X\big((\boldsymbol{\sigma}, \boldsymbol{\mu}, A^0!, I)\big) \ \boldsymbol{\mu}{\mathrm{g}} & \quad\equiv\quad g \ \boldsymbol{\mu}{\mathrm{pc}} & \quad\equiv\quad 0 \ \boldsymbol{\mu}{\mathbf{m}} & \quad\equiv\quad (0, 0, ...) \ \boldsymbol{\mu}{\mathrm{i}} & \quad\equiv\quad 0 \ \boldsymbol{\mu}{\mathbf{s}} & \quad\equiv\quad () \ \boldsymbol{\mu}_{\mathbf{o}} & \quad\equiv\quad () \end{aligned} $$
$$ X\big( (\boldsymbol{\sigma}, \boldsymbol{\mu}, A, I) \big) \equiv \begin{cases} \big(\varnothing, \boldsymbol{\mu}, A^0, I, \varnothing\big) & \text{if} \quad Z(\boldsymbol{\sigma}, \boldsymbol{\mu}, I) \ \big(\varnothing, \boldsymbol{\mu}', A^0, I, \mathbf{o}\big) & \text{if} \quad w = \text{\small REVERT} \ O(\boldsymbol{\sigma}, \boldsymbol{\mu}, A, I) \cdot \mathbf{o} & \text{if} \quad \mathbf{o} \neq \varnothing \ X\big(O(\boldsymbol{\sigma}, \boldsymbol{\mu}, A, I)\big) & \text{otherwise} \ \end{cases} $$
where
$$ \begin{aligned} \mathbf{o} & \quad\equiv\quad H(\boldsymbol{\mu}, I) \ (a, b, c, d) \cdot e & \quad\equiv\quad (a, b, c, d, e) \ \boldsymbol{\mu}' & \quad\equiv\quad \boldsymbol{\mu}\ \text{except:} \ \boldsymbol{\mu}'{\mathrm{g}} & \quad\equiv\quad \boldsymbol{\mu}{\mathrm{g}} - C(\boldsymbol{\sigma}, \boldsymbol{\mu}, I) \end{aligned} $$
其中
- $X$
- 循环调用直到遇到异常或执行完成
- $O$
- 单步执行当前指令 $w$
- 参考 (146)
- $Z$
- 检查是否异常
- 参考 (140)
- $o$
- $H$ 的返回结果
- $H$
- 检查是否正常终止
- 返回 $\varnothing$ 空,表示继续执行
- 返回 $()$ 空集,表示停止执行
- 否则,表示有意识的停止执行并附加执行结果 $o$
- 参考 (145)
- $C(\boldsymbol{\sigma}, \boldsymbol{\mu}, I)$
- 参考 (314)
- Appendix H.1. Gas Cost
- $\boldsymbol{\mu}_{\mathrm{g}}$
- 剩余可用 gas
- $\boldsymbol{\mu}_{\mathrm{pc}}$
- program counter
- $\boldsymbol{\mu}_{\mathbf{m}}$
- memory contents
- $\boldsymbol{\mu}_{\mathrm{i}}$
- active number of words in memory
- $\boldsymbol{\mu}_{\mathbf{s}}$
- stack contents
- $\boldsymbol{\mu}_{\mathbf{o}}$
- 执行输出 output
注意
- 公式 (146),执行函数 $\Xi$ 后,会丢弃 $I'$ 并记录 $\boldsymbol{\mu}'_{\mathrm{g}}$ 和 $o$
9.4.1 Machine State
机器状态 $\boldsymbol{\mu}$ 组成为 $(g, pc, \mathbf{m}, i, \mathbf{s})$
(139) 当前待执行的指令 $w$
$$ w \equiv \begin{cases} I{\mathbf{b}}[\boldsymbol{\mu}{\mathrm{pc}}] & \text{if} \quad \boldsymbol{\mu}{\mathrm{pc}} < \lVert I{\mathbf{b}} \rVert \ \text{{\small STOP}} & \text{otherwise} \end{cases} $$
// github.com/ethereum/go-ethereum@v1.10.6/core/vm/interpreter.go
func (in *EVMInterpreter) Run(contract *Contract, input []byte, readOnly bool) (ret []byte, err error)
op = contract.GetOp(pc)
operation := in.cfg.JumpTable[op]
// github.com/ethereum/go-ethereum@v1.10.6/core/vm/contract.go
// GetOp returns the n'th element in the contract's byte array
func (c *Contract) GetOp(n uint64) OpCode {
return OpCode(c.GetByte(n))
}
// GetByte returns the n'th byte in the contract's byte array
func (c *Contract) GetByte(n uint64) byte {
if n < uint64(len(c.Code)) {
return c.Code[n]
}
return 0 // STOP
}9.4.2 Exception Halting
公式 (140) (141) 异常检查函数 $Z$
$$ \begin{aligned} Z(\boldsymbol{\sigma}, \boldsymbol{\mu}, I) \quad\equiv\quad & \boldsymbol{\mu}_g < C(\boldsymbol{\sigma}, \boldsymbol{\mu}, I) \quad \vee \ & \mathbf{\delta}w = \varnothing \quad \vee \ & \lVert\boldsymbol{\mu}\mathbf{s}\rVert < \mathbf{\delta}w \quad \vee \ & ( w = \text{\small JUMP} \; \wedge \; \boldsymbol{\mu}\mathbf{s}[0] \notin D(I\mathbf{b}) ) \quad \vee \ & ( w = \text{\small JUMPI} \; \wedge \; \boldsymbol{\mu}\mathbf{s}[1] \neq 0 \; \wedge\boldsymbol{\mu}\mathbf{s}[0] \notin D(I\mathbf{b}) ) \quad \vee \ & ( w = \text{\small RETURNDATACOPY} \; \wedge \boldsymbol{\mu}{\mathbf{s}}[1] + \boldsymbol{\mu}{\mathbf{s}}[2] > \lVert\boldsymbol{\mu}{\mathbf{o}}\rVert) \quad \vee \ & \lVert\boldsymbol{\mu}\mathbf{s}\rVert - \mathbf{\delta}_w + \mathbf{\alpha}w > 1024 \quad \vee \ & ( \neg I{\mathrm{w}} \; \wedge \; W(w, \boldsymbol{\mu}) ) \quad \vee \ & ( w = \text{\small SSTORE} \; \wedge \; \boldsymbol{\mu}g \leqslant G{\mathrm{callstipend}} ) \end{aligned} $$
where
$$ \begin{aligned} W(w, \boldsymbol{\mu}) \quad\equiv\quad & w \in {\text{\small CREATE}, \text{\small CREATE2}, \text{\small SSTORE}, \text{\small SELFDESTRUCT}} \ \vee \ & \text{\small LOG0} \le w \; \wedge \; w \le \text{\small LOG4} \quad \vee \ & w = \text{\small CALL} \; \wedge \; \boldsymbol{\mu}_{\mathbf{s}}[2] \neq 0 \end{aligned} $$
其中
- $\delta$
- 指令 $w$ 的出栈个数
- $\alpha$
- 指令 $w$ 的入栈个数
- 栈的索引
- 从上往下增长
- 栈顶为0
异常情况
// github.com/ethereum/go-ethereum@v1.10.6/core/vm/errors.go
// List evm execution errors
var (
ErrOutOfGas = errors.New("out of gas")
ErrCodeStoreOutOfGas = errors.New("contract creation code storage out of gas")
ErrDepth = errors.New("max call depth exceeded")
ErrInsufficientBalance = errors.New("insufficient balance for transfer")
ErrContractAddressCollision = errors.New("contract address collision")
ErrExecutionReverted = errors.New("execution reverted")
ErrMaxCodeSizeExceeded = errors.New("max code size exceeded")
ErrInvalidJump = errors.New("invalid jump destination")
ErrWriteProtection = errors.New("write protection")
ErrReturnDataOutOfBounds = errors.New("return data out of bounds")
ErrGasUintOverflow = errors.New("gas uint64 overflow")
ErrInvalidCode = errors.New("invalid code: must not begin with 0xef")
ErrStackUnderflow = errors.New(fmt.Sprintf("stack underflow (%d <=> %d)", e.stackLen, e.required))
ErrStackOverflow = errors.New(fmt.Sprintf("stack limit reached %d (%d)", e.stackLen, e.limit))
ErrInvalidOpCode = errors.New(fmt.Sprintf("invalid opcode: %s", e.opcode))
)9.4.3 Jump Destionation Validity 跳转地址验证
公式 (142) (143) (144)
$$ D(\mathbf{c}) \equiv D_{\mathrm{J}}(\mathbf{c}, 0) $$
where:
$$ D{\mathrm{J}}(\mathbf{c}, i) \equiv \begin{cases} {} & \text{if} \quad i \geqslant \lVert \mathbf{c} \rVert \ { i } \cup D{\mathrm{J}}(\mathbf{c}, N(i, \mathbf{c}[i])) & \text{if} \quad \mathbf{c}[i] = \text{\small JUMPDEST} \ D_{\mathrm{J}}(\mathbf{c}, N(i, \mathbf{c}[i])) & \text{otherwise} \ \end{cases} $$
$$ N(i, w) \equiv \begin{cases} i + w - \text{\small PUSH1} + 2 & \text{if} \quad w \in [\text{\small PUSH1}, \text{\small PUSH32}] \ i + 1 & \text{otherwise} \end{cases} $$
其中
- $\mathbf{c}$
- 当前执行中的一段代码
- $D$ TODO
- 计算 $\mathbf{c}$ 的有效跳转地址的集合
- 按 ${\small JUMPDEST}$ 指令的位置来定义
- $N$ TODO
- 下一有效指令在代码 $\mathbf{c}$ 中的位置
- 且忽略 $\text{\small PUSH1}$ 指令的数据(如果有的话)
9.4.4 Normal Halting
(145) 正常停止检查函数 $H$
$$ H(\boldsymbol{\mu}, I) \equiv \begin{cases} H_{\text{\tiny RETURN}}(\boldsymbol{\mu}) & \text{if} \quad w \in {\text{\small {RETURN}}, \text{\small REVERT}} &\ () & \text{if} \quad w \in { \text{\small {STOP}}, \text{\small {SELFDESTRUCT}} } &\ \varnothing & \text{otherwise} \end{cases} $$
有3种可能的输出
其中
- $H_{\text{\tiny RETURN}}$
- 表示有意识地停止执行并附加执行结果 $o$
- 参考 # Appendix H. Virtual Machine Specification
- $H{\text{\tiny RETURN}}(\boldsymbol{\mu}) \equiv \boldsymbol{\mu}{\mathbf{m}}[ \boldsymbol{\mu}{\mathbf{s}}[0] \dots ( \boldsymbol{\mu}{\mathbf{s}}[0] + \boldsymbol{\mu}_{\mathbf{s}}[1] - 1 ) ]$
- $()$ 空集
- 表示停止执行
- $\varnothing$ 空
- 表示继续执行
9.5 The Execution Cycle 执行循环
公式 (146) (147) (148) (149)
$$ \begin{aligned} O\big((\boldsymbol{\sigma}, \boldsymbol{\mu}, A, I)\big) & \quad\equiv\quad (\boldsymbol{\sigma}', \boldsymbol{\mu}', A', I) \ \Delta & \quad\equiv\quad \mathbf{\alpha}{w} - \mathbf{\delta}{w} \ \lVert\boldsymbol{\mu}'{\mathbf{s}}\rVert & \quad\equiv\quad \lVert\boldsymbol{\mu}{\mathbf{s}}\rVert + \Delta \ \quad \forall x \in [\mathbf{\alpha}{w}, \lVert\boldsymbol{\mu}'{\mathbf{s}}\rVert): \boldsymbol{\mu}'{\mathbf{s}}[x] & \quad\equiv\quad \boldsymbol{\mu}{\mathbf{s}}[x-\Delta] \end{aligned} $$
其中
- $\delta$
- 指令 $w$ 的出栈个数
- $\alpha$
- 指令 $w$ 的入栈个数
- $\Delta$
- 栈大小的变化
- 栈的索引
- 从上往下增长
- 栈顶为0
公式 (150) (151)
$$ \begin{aligned} \boldsymbol{\mu}'{\mathrm{g}} & \quad\equiv\quad \boldsymbol{\mu}{\mathrm{g}} - C(\boldsymbol{\sigma}, \boldsymbol{\mu}, I) \ \boldsymbol{\mu}'{\mathrm{pc}} & \quad\equiv\quad \begin{cases} {J{\text{JUMP}}}(\boldsymbol{\mu}) & \text{if} \quad w = \text{\small JUMP} \ {J{\text{JUMPI}}}(\boldsymbol{\mu}) & \text{if} \quad w = \text{\small JUMPI} \ N(\boldsymbol{\mu}{\mathrm{pc}}, w) & \text{otherwise} \end{cases} \end{aligned} $$
其中
- $N$
- 参考 (144)
公式 (152) (153) (154) (155)
$$ \begin{aligned} \boldsymbol{\mu}'{\mathbf{m}} & \quad\equiv\quad \boldsymbol{\mu}{\mathbf{m}} \ \boldsymbol{\mu}'{\mathrm{i}} & \quad\equiv\quad \boldsymbol{\mu}{\mathrm{i}} \ A' & \quad\equiv\quad A \ \boldsymbol{\sigma}' & \quad\equiv\quad \boldsymbol{\sigma} \end{aligned} $$
通常我们假定内存($\boldsymbol{\mu}'{\mathbf{m}}$, $\boldsymbol{\mu}'{\mathbf{i}}$),自毁集合,世界状态不会被修改
具体参考 # Appendix H. Virtual Machine Specification
10. Blocktree to Blockchain 区块树到区块链
(156) (157) 区块难度计算函数
$$ \begin{aligned} B{\mathrm{t}} & \equiv B'{\mathrm{t}} + B{\mathrm{d}} \ B' & \equiv P(B{\mathrm{H}}) \end{aligned} $$
其中
- $B$
- 一个区块
- $B'$
- 父区块
- $B_{\mathrm{t}}$
- 区块总难度
- $B_{\mathrm{d}}$
- 当前区块的难度
11. Block Finalization 区块定稿
区块定稿要经过 4 步验证
- 验证叔块 Ommer Validation
- 验证交易 Transaction Validation
- 奖励发放 Reward Application
- 验证状态和 nonce State & Nonce Validation
11.1 Ommer Validation 验证 Ommer
(158) (159) (160)
$$ \lVert B{\mathbf{U}} \rVert \leqslant 2 \bigwedge{\mathbf{U} \in B{\mathbf{U}}} {V({\mathbf{U}}})\; \wedge \; k({\mathbf{U}}, P(\mathbf{B}{\mathbf{H}})_{\mathbf{H}}, 6) \ $$
$$ k(U, H, n) \equiv \begin{cases} \mathit{false} & \text{if} \quad n = 0 \ s(U, H) \vee \; k(U, P(H)_{\mathrm{H}}, n - 1) & \text{otherwise} \end{cases} $$
$$ s(U, H) \equiv (P(H) = P(U)\; \wedge \; H \neq U \; \wedge \; U \notin B(H)_{\mathbf{U}}) $$
验证
- 当前区块头最多有2个叔块
- 叔块头列表自身有效,且表示的叔块与当前区块在6代以内
其中
- $k$
- is-kin 是亲属
- $s$
- is-sibling 是兄妹
- $V$
- 区块头验证函数
- 参考公式 (51)
11.2 Transaction Validation 交易验证
$$ {B{\mathrm{H}}}{\mathrm{g}} = {\ell}({\mathbf{R})_{\mathrm{u}}} $$
其中
- ${B{\mathrm{H}}}{\mathrm{g}}$
- 当前区块头中的累计使用 gas
- ${\ell}({\mathbf{R})_{\mathrm{u}}}$
- 当前区块中最后一条收据的累计使用 gas
11.3 Reward Application 奖励发放
公式 (162) (163) (164) (165) (166) $\Omega$ 区块奖励函数
$$ \begin{aligned} \Omega(B, \boldsymbol{\sigma}) & \quad\equiv\quad \boldsymbol{\sigma}': \boldsymbol{\sigma}' = \boldsymbol{\sigma} \quad \text{except:} \ \qquad\boldsymbol{\sigma}'[{\mathbf{B}{\mathrm{H}}}{\mathrm{c}}]{\mathrm{b}} & \quad=\quad \boldsymbol{\sigma}[{\mathbf{B}{\mathrm{H}}}{\mathrm{c}}]{\mathrm{b}} + \left(1 + \frac{\lVert \mathbf{B}{\mathbf{U}}\rVert}{32}\right)R{\mathrm{block}} \ \forall \mathbf{U} \in \mathbf{B}{\mathbf{U}}:\quad \boldsymbol{\sigma}'[\mathbf{U}{\mathrm{c}}] & \quad=\quad \begin{cases} \varnothing &\text{if}\ \boldsymbol{\sigma}[\mathbf{U}{\mathrm{c}}] = \varnothing\ \wedge\ R = 0 \ \mathbf{a}' &\text{otherwise} \end{cases} \ \mathbf{a}' & \quad\equiv\quad (\boldsymbol{\sigma}[U{\mathrm{c}}]{\mathrm{n}}, \boldsymbol{\sigma}[U{\mathrm{c}}]{\mathrm{b}} + R, \boldsymbol{\sigma}[U{\mathrm{c}}]{\mathbf{s}}, \boldsymbol{\sigma}[U{\mathrm{c}}]{\mathrm{c}}) \ R & \quad\equiv\quad \left(1 + \frac{1}{8} (U{\mathrm{i}} - {B{\mathrm{H}}}{\mathrm{i}})\right) R_{\mathrm{block}} \end{aligned} $$
其中
- $\mathbf{B}_{\mathbf{U}}$
- 当前区块内的叔块头列表
- ${\mathbf{B}{\mathrm{H}}}{\mathrm{c}}$
- 当前区块头中存储的 beneficiary
- 即当前区块收益的归属地址
- $U_{\mathrm{c}}$
- 叔块收益的归属地址
(167) ${R_{block}}$ 定义
$$ R{\mathrm{block}} = 10^{18} \times \begin{cases} 5 &\text{if}\ H{\mathrm{i}} < F{\mathrm{Byzantium}} \ 3 &\text{if}\ F{\mathrm{Byzantium}} \leqslant H{\mathrm{i}} < F{\mathrm{Constantinople}} \ 2 &\text{if}\ H{\mathrm{i}} \geqslant F{\mathrm{Constantinople}} \ \end{cases} \ $$
11.4 State & Nonce Validation 状态和 nonce 验证
(168) 映射 Block 到世界状态的函数 $\Gamma$
$$ \Gamma(B) \equiv \begin{cases} \boldsymbol{\sigma}0 & \text{if} \quad P(B{\mathrm{H}}) = \varnothing \ \boldsymbol{\sigma}{\mathrm{i}}: \mathtt{{TRIE}}(L{\mathrm{S}}(\boldsymbol{\sigma}{\mathrm{i}})) = {P(B{\mathrm{H}}){\mathrm{H}}}{\mathrm{r}} & \text{otherwise} \end{cases} $$
其中
- $L_S$
- 世界状态坍塌函数
- 参考 (10)
- $\mathtt{{TRIE}}(L{\mathrm{S}}(\boldsymbol{\sigma}{\mathrm{i}})) = {P(B{\mathrm{H}}){\mathrm{H}}}_{\mathrm{r}}$
- 判断 state TRIE 根节点的内容 等于 区块头的 stateRoot
- 理解
- 不像 Block 存储在区块链上,TRIE 树结构是通过存储在客户端数据库中的数据构造出来的
- 因此需要比较区块头存储中的 stateRoot hash,是否与构造 TRIE 树时层层计算出来的根节点 hash 相等
(169) (170) (171) (172) 区块级别状转换函数 $\Phi$
$$ \begin{aligned} \Phi(B) & \quad\equiv\quad B': \quad B' = B^ \quad \text{except:} \ B'{\mathrm{n}} & \quad=\quad n: \quad x \leqslant \frac{2^{256}}{{H{\mathrm{d}}}} \ B'_{\mathrm{m}} & \quad=\quad m \quad \text{with } (x, m) = \mathtt{PoW}(B^{{\cancel{n}}}, n, \mathbf{d}) \ B^ & \quad\equiv\quad B \quad \text{except:} \quad {{B^{\mathrm{r}}}} = {r}({\Pi}(\Gamma(B), B)) \end{aligned} $$
$\Phi$ 函数计算 nonce 和 mixHash 后分别设置到 $B'{\mathrm{n}}$ 和 $B'{\mathrm{m}}$
其中
- $\mathbf{d}$
- $\Pi$
- 区块级状态转换函数
- 参考公式 (177)
- $\Omega$
- 区块奖励函数
(173) 第 n 个状态 $\boldsymbol{\sigma}[n]$
$$ \boldsymbol{\sigma}[n] = \begin{cases} {\Gamma}(B) & \text{if} \quad n < 0 \ {\Upsilon}(\boldsymbol{\sigma}[n - 1], B_{\mathbf{T}}[n]) & \text{otherwise} \end{cases} $$
(174) (175) (176) $\Upsilon^{\mathbf{u}}$ $\Upsilon^{\mathbf{l}}$ $\Upsilon^{\mathbf{z}}$ 的定义/赋值
$$ \begin{aligned} \mathbf{R}[n]{\mathrm{u}} = \begin{cases} 0 & \text{if} \quad n < 0 \ \Upsilon^g(\boldsymbol{\sigma}[n - 1], B{\mathbf{T}}[n]) \quad + \mathbf{R}[n-1]_{\mathrm{u}} & \text{otherwise} \end{cases} \end{aligned} $$
$$ \mathbf{R}[n]{\mathbf{l}} = \Upsilon^{\mathbf{l}}(\boldsymbol{\sigma}[n - 1], B{\mathbf{T}}[n]) $$
$$ \mathbf{R}[n]{\mathrm{z}} = \Upsilon^{\mathrm{z}}(\boldsymbol{\sigma}[n - 1], B{\mathbf{T}}[n]) $$
其中
- $R_{\mathrm{u}}$
- 当前区块中,交易发生后的累积 gas 使用量
- $R_{\mathrm{l}}$
- 交易过程中创建的一系列日志
- $R_{\mathrm{z}}$
- 交易的状态码
- $R_{\mathrm{b}}$
- 由一系列日志构成的 Bloom 过滤器
- 参考公式 (26) (27) (28) (29) (30)
公式 (177) 区块级状态转换函数 $\Pi$
$$ \Pi(\boldsymbol{\sigma}, B) \equiv {\Omega}(B, \ell(\boldsymbol{\sigma})) $$
对区块应用区块奖励函数 ${\Omega}$,可以得到最新的世界状态,即最终的区块级状态转换
Appendix B. Recursive Length Prefix
Appendix C. Hex-Prefix Encoding
公式 (189) (190)
$$ \begin{aligned} \mathtt{HP}(\mathbf{x}, t): \mathbf{x} \in \mathbb{Y} \equiv \begin{cases} (16f(t), 16\mathbf{x}[0] + \mathbf{x}[1], 16\mathbf{x}[2] + \mathbf{x}[3], ...) & \text{if} \lVert \mathbf{x} \rVert \; \text{is even} \ (16(f(t) + 1) + \mathbf{x}[0], 16\mathbf{x}[1] + \mathbf{x}[2], 16\mathbf{x}[3] + \mathbf{x}[4], ...) & \text{otherwise} \end{cases} \ \end{aligned} $$
$$ \begin{aligned} f(t) & \equiv & \begin{cases} 2 & \text{if} \quad t \neq 0 \ 0 & \text{otherwise} \end{cases} \end{aligned} $$
参考
// https://github.com/ethereum/go-ethereum/blob/master/trie/encoding.go
// https://github.com/sontuphan/debug-geth/blob/master/trie/encoding.go
// This block of code does Compact (hex-prefix) encoding as following table
// hex char bits | node type partial path length
// 0 0000 | extension even
// 1 0001 | extension odd
// 2 0010 | terminating (leaf) even
// 3 0011 | terminating (leaf) odd
func hexToCompact(hex []byte) []byte {
terminator := byte(0)
if hasTerm(hex) {
terminator = 1
hex = hex[:len(hex)-1]
}
buf := make([]byte, len(hex)/2+1)
buf[0] = terminator << 5 // the flag byte
if len(hex)&1 == 1 {
buf[0] |= 1 << 4 // odd flag
buf[0] |= hex[0] // first nibble is contained in the first byte
hex = hex[1:]
}
decodeNibbles(hex, buf[1:])
return buf
}- 输入
- hex
- 16进制明文字符串 path
- 每个字符占用一个字节,取值范围是 [0-9, a-f]
- 可能在 path 尾部追加最后一个字节,值为 0x10,表示 terminator
- 即 hex 是个叶子节点(包含 value),而非中间节点
- 输出
- buf (Hex-Prefix 编码得到的二进制字符串 )
- 添加半个字节(一个hex编码)到 hex 前面,用于表示
- hex 是否包含 terminator
- hex 移除 terminator 后(如果有的话),长度是奇数还是偶数
- 确保 buf 的长度是偶数
例子
| Row | Node Type | Path Length | Path Before Encoding(In HEX) | Path After Encoding(In HEX) |
|---|---|---|---|---|
| 0 | Extension | EVEN | [0, 1, 2, 3, 4, 5] | '00 01 23 45' |
| 1 | Extension | ODD | [1, 2, 3, 4, 5] | '11 23 45' |
| 2 | Leaf(has terminator(10)) | EVEN | [0, f, 1, c, b, 8, 10] | '20 0f 1c b8' |
| 3 | Leaf(has terminator(10)) | ODD | [f, 1, c, b, 8, 10] | '3f 1c b8' |
Appendix D. Modified Merkle Patricia Tree
参考
(191) (192) 数据集合 $\mathfrak{I}$
$$ \mathfrak{I} = { (\mathbf{k}_0 \in \mathbb{B}, \mathbf{v}_0 \in \mathbb{B}), (\mathbf{k}_1 \in \mathbb{B}, \mathbf{v}_1 \in \mathbb{B}), ... } \ \forall I \in \mathfrak{I}: I \equiv (I_0, I_1) $$
(193) (194)
任何 bytes 都可以看为半字节(nibbles 4bit)组成的序列
$$ \begin{aligned} y(\mathfrak{I}) & = { (\mathbf{k}_0' \in \mathbb{Y}, \mathbf{v}_0 \in \mathbb{B}), (\mathbf{k}_1' \in \mathbb{Y}, \mathbf{v}1 \in \mathbb{B}), ... } \ \forall n: \quad \forall i < 2\lVert\mathbf{k}{n}\rVert: \quad \mathbf{k}{n}'[i] & \equiv \begin{cases} \lfloor \mathbf{k}{n}[i \div 2] \div 16 \rfloor & \text{if} \; i \; \text{is even} \ \mathbf{k}_{n}[\lfloor i \div 2 \rfloor] \bmod 16 & \text{otherwise} \end{cases} \end{aligned} $$
公式 (195) 根节点函数 $\texttt{TRIE}$
$$ \texttt{TRIE}(\mathfrak{I}) \equiv \texttt{KEC}\big(\texttt{RLP} (c(\mathfrak{I}, 0))\big) $$
公式 (196)
$$ n(\mathfrak{I}, i) \equiv \begin{cases} () & \text{if} \quad \mathfrak{I} = \varnothing \ c(\mathfrak{I}, i) & \text{if} \quad \lVert \, \texttt{RLP} \big( c(\mathfrak{I}, i) \big) \rVert < 32 \ \texttt{KEC}\big(\texttt{RLP}( c(\mathfrak{I}, i)) \big) & \text{otherwise} \end{cases} $$
公式 (197)
$$ \begin{aligned} c(\mathfrak{I}, i) \equiv \begin{cases} \big(\texttt{HP}(I_0[i .. (\lVert I_0\rVert - 1)], 1), I_1 \big) & \text{if} \ \lVert \mathfrak{I} \rVert = 1 \text{where} \ \exists I: I \in \mathfrak{I} \ \big(\texttt{HP}(I_0[i .. (j - 1)], 0), n(\mathfrak{I}, j) \big) & \text{if} \ i \ne j \ \text{where} \ j = \max { x : \exists \mathbf{l}: \lVert \mathbf{l} \rVert = x \wedge \forall I \in \mathfrak{I}: I_0[0 .. (x - 1)] = \mathbf{l} } \ (u(0), u(1), ..., u(15), v) & \text{otherwise} \ \text{where} \ & u(j) \equiv n({ I : I \in \mathfrak{I} \wedge I_0[i] = j }, i + 1) \ & v = \begin{cases} I_1 & \text{if} \ \exists I: I \in \mathfrak{I} \wedge \lVert I_0 \rVert = i \ () & \text{otherwise} \end{cases} \end{cases} \end{aligned} $$
其中
- 叶子节点 Lea
- 包含两个字段
- 第一个字段是剩下的 Key 的 HP 编码(HP 的第二个参数为1)
- 第二个字段是 Value
- 扩展节点 Extension
- 包含两个字段
- 第一个字段是剩下的 Key 的可以至少被两个剩下节点共享的最大公共前缀((HP 的第二个参数为0)
- 第二个字段是 $n(\mathfrak{I}, j)$
- 分支节点 Branch
- 包含17个字段
- 前16个项目对应于 [0-9,a-f]
- 第17个字段是存储在当前结点结束的节点
- 例如
- 有三个key,分别是 abc,abd,ab
- 第17个字段储存了ab节点的值
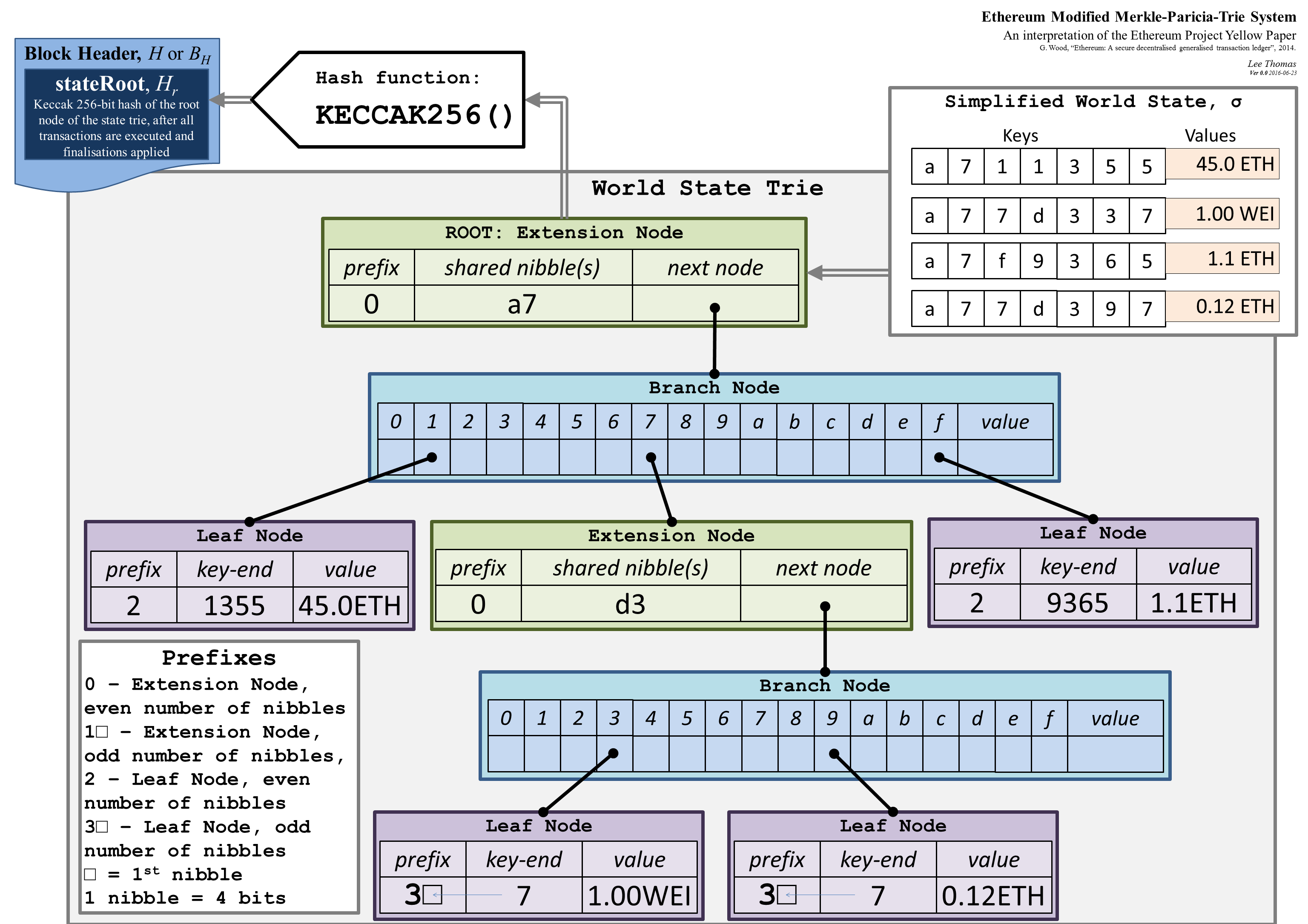
图片来源 ELI5 How does a Merkle-Patricia-trie tree work?
Appendix H. Virtual Machine Specification
注意区分单位
$\boldsymbol{\mu}{\mathbf{s}}$ / $\boldsymbol{\sigma}[a]{\mathbf{s}}$ 以 32 字节为单位
$\boldsymbol{\mu}_{\mathbf{m}}$ 以 1 字节为单位
参考 SSTORE/SLOAD, MSTORE/MLOAD
H.2. Instruction Set
参考 Difference between CALL, CALLCODE and DELEGATECALL
DELEGATECALL was a new opcode that was a bug fix for CALLCODE which did not preserve msg.sender and msg.value. If Alice invokes Bob who does DELEGATECALL to Charlie, the msg.sender in the DELEGATECALL is Alice (whereas if CALLCODE was used the msg.sender would be Bob).
- 深入探索 CALL 指令参数0 5011 浏览

