深入探索 CALL 指令参数0
- ripwu
- 发布于 2021-10-25 09:58
- 阅读 4988
CALL 指令参数0 的用途,以及外部调用中 gas 的计算
此前和几位朋友交流过智能合约外部调用的问题,有点久了;最近开始有些时间,简单整理记录下
外部调用有好几种指令,下面以最常见的 CALL 为例
问题
讨论最多的是 CALL 指令的参数0 gas 具体的作用,比如:
问题一:参数0 是否无用,为什么 opCall() 中直接 pop 掉了?
func opCall(pc *uint64, interpreter *EVMInterpreter, scope *ScopeContext) ([]byte, error) {
stack := scope.Stack
// Pop gas. The actual gas in interpreter.evm.callGasTemp.
// We can use this as a temporary value
temp := stack.pop()
gas := interpreter.evm.callGasTemp
// Pop other call parameters.
addr, value, inOffset, inSize, retOffset, retSize := stack.pop(), stack.pop(), stack.pop(), stack.pop(), stack.pop(), stack.pop()
// Too Long Not Listed
// ...
}问题二:此前 Paradigm CTF 2021: BabySandbox 题解,能否稍做解释?
问题三:题解测试有效,但为什么修改原题,CALL 时 0x4000 改为 0x30000 的话,题解无效?
pragma solidity 0.7.0;
contract BabySandbox {
function run(address code) external payable {
assembly {
// if we're calling ourselves, perform the privileged delegatecall
if eq(caller(), address()) {
switch delegatecall(gas(), code, 0x00, 0x00, 0x00, 0x00)
case 0 {
returndatacopy(0x00, 0x00, returndatasize())
revert(0x00, returndatasize())
}
case 1 {
returndatacopy(0x00, 0x00, returndatasize())
return(0x00, returndatasize())
}
}
// ensure enough gas
if lt(gas(), 0xf000) {
revert(0x00, 0x00)
}
// load calldata
calldatacopy(0x00, 0x00, calldatasize())
// run using staticcall
// if this fails, then the code is malicious because it tried to change state
if iszero(staticcall(0x4000, address(), 0, calldatasize(), 0, 0)) {
revert(0x00, 0x00)
}
// if we got here, the code wasn't malicious
// run without staticcall since it's safe
switch call(0x4000, address(), 0, 0, calldatasize(), 0, 0)
case 0 {
returndatacopy(0x00, 0x00, returndatasize())
// revert(0x00, returndatasize())
}
case 1 {
returndatacopy(0x00, 0x00, returndatasize())
return(0x00, returndatasize())
}
}
}
}定义
黄皮书关于 gas 机制的介绍,确实比较散乱..
要解释上面的问题,首先需要理解 CALL 的定义:
$$ \mathbf{i} \equiv \boldsymbol{\mu}{\mathbf{m}}[ \boldsymbol{\mu}{\mathbf{s}}[3] \dots (\boldsymbol{\mu}{\mathbf{s}}[3] + \boldsymbol{\mu}{\mathbf{s}}[4] - 1) ] $$
$$ \begin{aligned} (\boldsymbol{\sigma}', g', A^+, \mathbf{o}) \equiv \begin{cases}{\Theta}(\boldsymbol{\sigma}, I{\mathrm{a}}, I{\mathrm{o}}, t, t, C{\text{\tiny CALLGAS}}(\boldsymbol{\mu}), I{\mathrm{p}}, \boldsymbol{\mu}{\mathbf{s}}[2], \boldsymbol{\mu}{\mathbf{s}}[2], \mathbf{i}, I{\mathrm{e}} + 1, I{\mathrm{w}}) & \text{if} \ \boldsymbol{\mu}{\mathbf{s}}[2] \leqslant \boldsymbol{\sigma}[I{\mathrm{a}}]{\mathrm{b}} \;\wedge I{\mathrm{e}} < 1024 \ (\boldsymbol{\sigma}, g, \varnothing, ()) & \text{otherwise} \end{cases} \end{aligned} $$
$$ n \equiv \min({ \boldsymbol{\mu}_{\mathbf{s}}[6], \lVert \mathbf{o} \rVert}) $$
$$ \boldsymbol{\mu}'{\mathbf{m}}[ \boldsymbol{\mu}{\mathbf{s}}[5] \dots (\boldsymbol{\mu}_{\mathbf{s}}[5] + n - 1) ] = \mathbf{o}[0 \dots (n - 1)] $$
$$ \boldsymbol{\mu}'_{\mathbf{o}} = \mathbf{o} $$
$$ \boldsymbol{\mu}'{\mathrm{g}} \equiv \boldsymbol{\mu}{\mathrm{g}} + g' $$
$$ \boldsymbol{\mu}'_{\mathbf{s}}[0] \equiv x $$
$$ A' \equiv A \Cup A^+ $$
$$ t \equiv \boldsymbol{\mu}_{\mathbf{s}}[1] \bmod 2^{160} $$
where $x=0$ if the code execution for this operation failed due to an ${exceptional\ halting}$ (or for a $\text{\small REVERT}$) $\boldsymbol{\sigma}' = \varnothing$ or if $\boldsymbol{\mu}{\mathbf{s}}[2] > \boldsymbol{\sigma}[I{\mathrm{a}}]{\mathrm{b}}$ (not enough funds) or $I{\mathrm{e}} = 1024$ (call depth limit reached); $x=1$ otherwise.
$$ \boldsymbol{\mu}'{\mathrm{i}} \equiv M(M(\boldsymbol{\mu}{\mathrm{i}}, \boldsymbol{\mu}{\mathbf{s}}[3], \boldsymbol{\mu}{\mathbf{s}}[4]), \boldsymbol{\mu}{\mathbf{s}}[5], \boldsymbol{\mu}{\mathbf{s}}[6]) $$
Thus the operand order is: gas, to, value, in offset, in size, out offset, out size.
$$ C{\text{\tiny CALL}}(\boldsymbol{\sigma}, \boldsymbol{\mu}) \equiv C{\text{\tiny GASCAP}}(\boldsymbol{\sigma}, \boldsymbol{\mu}) + C_{\text{\tiny EXTRA}}(\boldsymbol{\sigma}, \boldsymbol{\mu}) $$
$$ C{\text{\tiny CALLGAS}}(\boldsymbol{\sigma}, \boldsymbol{\mu}) \equiv \begin{cases} C{\text{\tiny GASCAP}}(\boldsymbol{\sigma}, \boldsymbol{\mu}) + G{\mathrm{callstipend}} & \text{if} \quad \boldsymbol{\mu}{\mathbf{s}}[2] \neq 0 \ C_{\text{\tiny GASCAP}}(\boldsymbol{\sigma}, \boldsymbol{\mu}) & \text{otherwise} \end{cases} $$
$$ C{\text{\tiny GASCAP}}(\boldsymbol{\sigma}, \boldsymbol{\mu}) \equiv \begin{cases} \min{ L(\boldsymbol{\mu}{\mathrm{g}} - C{\text{\tiny EXTRA}}(\boldsymbol{\sigma}, \boldsymbol{\mu})), \boldsymbol{\mu}{\mathbf{s}}[0] } & \text{if} \quad \boldsymbol{\mu}{\mathrm{g}} \ge C{\text{\tiny EXTRA}}(\boldsymbol{\sigma}, \boldsymbol{\mu}) \ \boldsymbol{\mu}_{\mathbf{s}}[0] & \text{otherwise}\end{cases} $$
$$ C{\text{\tiny EXTRA}}(\boldsymbol{\sigma}, \boldsymbol{\mu}) \equiv G{\mathrm{call}} + C{\text{\tiny XFER}}(\boldsymbol{\mu}) + C{\text{\tiny NEW}}(\boldsymbol{\sigma}, \boldsymbol{\mu}) $$
$$ C{\text{\tiny XFER}}(\boldsymbol{\mu}) \equiv \begin{cases}G{\mathrm{callvalue}} & \text{if} \quad \boldsymbol{\mu}_{\mathbf{s}}[2] \neq 0 \0 & \text{otherwise} \end{cases} $$
$$ C{\text{\tiny NEW}}(\boldsymbol{\sigma}, \boldsymbol{\mu}) \equiv \begin{cases} G{\mathrm{newaccount}} & \text{if} \quad \mathtt{DEAD}(\boldsymbol{\sigma}, \boldsymbol{\mu}{\mathbf{s}}[1] \bmod 2^{160}) \wedge \boldsymbol{\mu}{\mathbf{s}}[2] \neq 0 \ 0 & \text{otherwise}\end{cases} $$
资料
除了 CALL 自身定义外,可能还需要参考附录:
Appendix G. Fee Schedule
Appendix H. Virtual Machine Specification H.1. Gas Cost
填坑
Paradigm CTF 2021: BabySandbox 题解挖了个坑,引出上面的问题二和问题三
这里尝试用另外一个坑的方式作为例子,算是把两个坑填一填~
在 Ethernaut 第13题 Gatekeeper One 题解中,有提到对某些 OPCODE 的 GAS 存在疑惑
比如题解中的测试交易,gas 消耗状况如下
| Step | PC | Operation | Gas | GasCost | Depth |
|---|---|---|---|---|---|
| [131] | 377 | EXTCODESIZE | 2976410 | 2600 | 1 |
| [132] | 378 | ISZERO | 2973810 | 3 | 1 |
| [133] | 379 | DUP1 | 2973807 | 3 | 1 |
| [134] | 380 | ISZERO | 2973804 | 3 | 1 |
| [135] | 381 | PUSH2 | 2973801 | 3 | 1 |
| [136] | 384 | JUMPI | 2973798 | 10 | 1 |
| [137] | 389 | JUMPDEST | 2973788 | 1 | 1 |
| [138] | 390 | POP | 2973787 | 2 | 1 |
| [139] | 391 | DUP8 | 2973785 | 3 | 1 |
| [140] | 392 | CALL | 2973782 | 2891523 | 1 |
| [141] | 0 | PUSH1 | 2891423 | 3 | 2 |
注意 [140],在准备调用 CALL 前,堆栈和内存如下
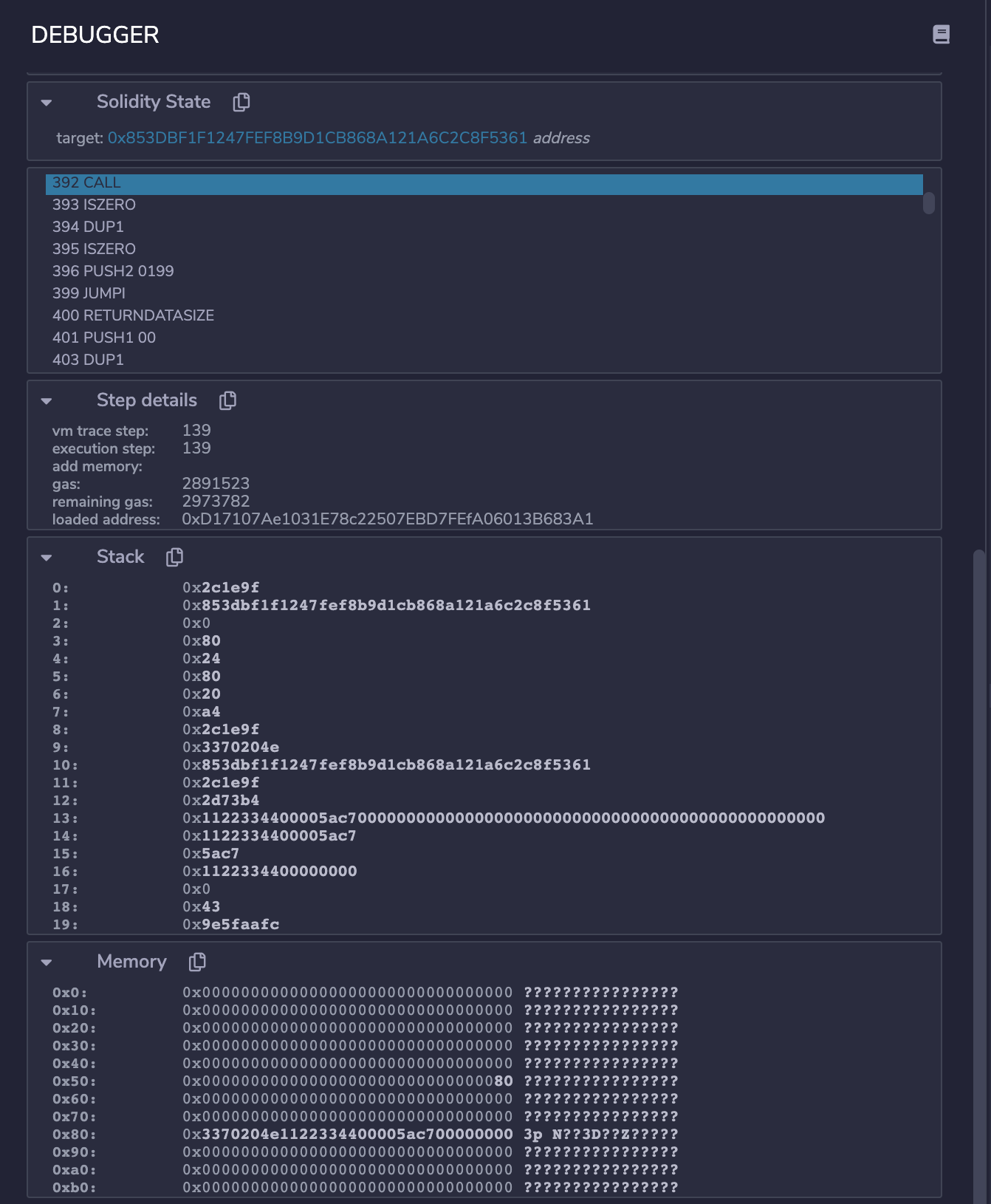
结合 CALL 定义的相关公式和上面截图,可知此时
$\boldsymbol{\mu}_{\mathbf{s}}[0] = 0x2c1e9f = 2891423$
$\boldsymbol{\mu}_{\mathbf{s}}[2] = 0$
$\boldsymbol{\mu}_{\mathrm{g}} = 2973782$
问题如下:
为什么 [141] 的 Gas 为 2891423,而 [140] 的 GasCost 为 2891523,这两个数字是怎么来的?
解答
上面例子中 $(\boldsymbol{\mu}{\mathbf{s}}[3], \boldsymbol{\mu}{\mathbf{s}}[4]) \gt (\boldsymbol{\mu}{\mathbf{s}}[5], \boldsymbol{\mu}{\mathbf{s}}[6])$
因此没有扩展内存,即内存相关的 gas 为 0
--
推导1 $C_{\text{\tiny EXTRA}}(\boldsymbol{\sigma}, \boldsymbol{\mu}) = 100$
已知公式
$$ C{\text{\tiny EXTRA}}(\boldsymbol{\sigma}, \boldsymbol{\mu}) \equiv G{\mathrm{call}} + C{\text{\tiny XFER}}(\boldsymbol{\mu}) + C{\text{\tiny NEW}}(\boldsymbol{\sigma}, \boldsymbol{\mu}) $$
$$ C{\text{\tiny XFER}}(\boldsymbol{\mu}) \equiv \begin{cases} G{\mathrm{callvalue}} & \text{if} \quad \boldsymbol{\mu}_{\mathbf{s}}[2] \neq 0 \ 0 & \text{otherwise} \end{cases} $$
$$ C{\text{\tiny NEW}}(\boldsymbol{\sigma}, \boldsymbol{\mu}) \equiv \begin{cases} G{\mathrm{newaccount}} & \text{if} \quad \mathtt{DEAD}(\boldsymbol{\sigma}, \boldsymbol{\mu}{\mathbf{s}}[1] \bmod 2^{160}) \wedge \boldsymbol{\mu}{\mathbf{s}}[2] \neq 0 \ 0 & \text{otherwise} \end{cases} $$
又有 $\boldsymbol{\mu}_{\mathbf{s}}[2]$ 为 0
因此 $C{\text{\tiny XFER}}(\boldsymbol{\mu}) = 0$ 且 $C{\text{\tiny NEW}}(\boldsymbol{\sigma}, \boldsymbol{\mu}) = 0$
因此 $C{\text{\tiny EXTRA}}(\boldsymbol{\sigma}, \boldsymbol{\mu}) = G{\mathrm{call}} + 0 + 0$
再查看编译得到的 OPCODE
GatekeeperOne(target).enter.gas(sendGas)(_gateKey);上面代码会先通过 EXTCODESIZE 检查 target 是否存在源码,然后 CALL 时再对 target 发起消息调用。
根据 EIP-2929: Gas cost increases for state access opcodes
前面 [131] 的 EXTCODESIZE 首次对该地址操作,消耗 2600 gas;因此接下来 [141] CALL 时,只需要消耗 100 gas,即 $G_{\mathrm{call}} = 100$
因此 $C{\text{\tiny EXTRA}}(\boldsymbol{\sigma}, \boldsymbol{\mu}) = G{\mathrm{call}} + 0 + 0 = 100$
// github.com/ethereum/go-ethereum@v1.10.6/params/protocol_params.go
const (
ColdAccountAccessCostEIP2929 = uint64(2600) // COLD_ACCOUNT_ACCESS_COST
WarmStorageReadCostEIP2929 = uint64(100) // WARM_STORAGE_READ_COST
)
// github.com/ethereum/go-ethereum@v1.10.6/core/vm/eips.go
func enable2929(jt *JumpTable) {
jt[CALL].constantGas = params.WarmStorageReadCostEIP2929
jt[CALL].dynamicGas = gasCallEIP2929
}
// github.com/ethereum/go-ethereum@v1.10.6/core/vm/operations_acl.go
var (
gasCallEIP2929 = makeCallVariantGasCallEIP2929(gasCall)
)
func makeCallVariantGasCallEIP2929(oldCalculator gasFunc) gasFunc {
return func(evm *EVM, contract *Contract, stack *Stack, mem *Memory, memorySize uint64) (uint64, error) {
addr := common.Address(stack.Back(1).Bytes20())
// Check slot presence in the access list
warmAccess := evm.StateDB.AddressInAccessList(addr)
// The WarmStorageReadCostEIP2929 (100) is already deducted in the form of a constant cost, so
// the cost to charge for cold access, if any, is Cold - Warm
coldCost := params.ColdAccountAccessCostEIP2929 - params.WarmStorageReadCostEIP2929
if !warmAccess {
evm.StateDB.AddAddressToAccessList(addr)
// Charge the remaining difference here already, to correctly calculate available
// gas for call
if !contract.UseGas(coldCost) {
return 0, ErrOutOfGas
}
}
// Now call the old calculator, which takes into account
// - create new account
// - transfer value
// - memory expansion
// - 63/64ths rule
gas, err := oldCalculator(evm, contract, stack, mem, memorySize)
if warmAccess || err != nil {
return gas, err
}
// In case of a cold access, we temporarily add the cold charge back, and also
// add it to the returned gas. By adding it to the return, it will be charged
// outside of this function, as part of the dynamic gas, and that will make it
// also become correctly reported to tracers.
contract.Gas += coldCost
return gas + coldCost, nil
}
}--
推导2 $C_{\text{\tiny GASCAP}}(\boldsymbol{\sigma}, \boldsymbol{\mu}) = 2891423$
已知公式
$$ C{\text{\tiny GASCAP}}(\boldsymbol{\sigma}, \boldsymbol{\mu}) \equiv \begin{cases} \min{ L(\boldsymbol{\mu}{\mathrm{g}} - C{\text{\tiny EXTRA}}(\boldsymbol{\sigma}, \boldsymbol{\mu})), \boldsymbol{\mu}{\mathbf{s}}[0] } & \text{if} \quad \boldsymbol{\mu}{\mathrm{g}} \ge C{\text{\tiny EXTRA}}(\boldsymbol{\sigma}, \boldsymbol{\mu})\ \boldsymbol{\mu}_{\mathbf{s}}[0] & \text{otherwise} \end{cases} $$
其中
(318)
$$ L(n) \equiv n - \lfloor n / 64 \rfloor $$
The Dark Side of Ethereum 1/64th CALL Gas Reduction
// github.com/ethereum/go-ethereum@v1.10.6/core/vm/gas.go
// callGas returns the actual gas cost of the call.
//
// The cost of gas was changed during the homestead price change HF.
// As part of EIP 150 (TangerineWhistle), the returned gas is gas - base * 63 / 64.
func callGas(isEip150 bool, availableGas, base uint64, callCost *uint256.Int) (uint64, error) {
if isEip150 {
availableGas = availableGas - base
gas := availableGas - availableGas/64
// If the bit length exceeds 64 bit we know that the newly calculated "gas" for EIP150
// is smaller than the requested amount. Therefore we return the new gas instead
// of returning an error.
if !callCost.IsUint64() || gas < callCost.Uint64() {
return gas, nil
}
}
if !callCost.IsUint64() {
return 0, ErrGasUintOverflow
}
return callCost.Uint64(), nil
}参考截图,这里 $\boldsymbol{\mu}{\mathbf{s}}[0]$ 为 2891423,$\boldsymbol{\mu}{\mathrm{g}}$ 为 2973782,且如上所述 $C_{\text{\tiny EXTRA}}(\boldsymbol{\sigma}, \boldsymbol{\mu})$ 为 100
因此 $C_{\text{\tiny GASCAP}}(\boldsymbol{\sigma}, \boldsymbol{\mu}) = \min{ (2973782 - 100) - \lfloor (2973782 - 100) / 64 \rfloor, 2891423 } = 2891423$
又根据公式
$$ C{\text{\tiny CALLGAS}}(\boldsymbol{\sigma}, \boldsymbol{\mu}) \equiv \begin{cases} C{\text{\tiny GASCAP}}(\boldsymbol{\sigma}, \boldsymbol{\mu}) + G{\mathrm{callstipend}} & \text{if} \quad \boldsymbol{\mu}{\mathbf{s}}[2] \neq 0 \ C_{\text{\tiny GASCAP}}(\boldsymbol{\sigma}, \boldsymbol{\mu}) & \text{otherwise} \end{cases} $$
因此 $C{\text{\tiny CALLGAS}}(\boldsymbol{\sigma}, \boldsymbol{\mu}) = C{\text{\tiny GASCAP}}(\boldsymbol{\sigma}, \boldsymbol{\mu}) = 2891423$
再根据公式
$$ \begin{aligned} (\boldsymbol{\sigma}', g', A^+, \mathbf{o}) \equiv \begin{cases}{\Theta}(\boldsymbol{\sigma}, I{\mathrm{a}}, I{\mathrm{o}}, t, t, C{\text{\tiny CALLGAS}}(\boldsymbol{\mu}), I{\mathrm{p}}, \boldsymbol{\mu}{\mathbf{s}}[2], \boldsymbol{\mu}{\mathbf{s}}[2], \mathbf{i}, I{\mathrm{e}} + 1, I{\mathrm{w}}) & \text{if} \ \boldsymbol{\mu}{\mathbf{s}}[2] \leqslant \boldsymbol{\sigma}[I{\mathrm{a}}]{\mathrm{b}} \;\wedge I{\mathrm{e}} < 1024 \ (\boldsymbol{\sigma}, g, \varnothing, ()) & \text{otherwise} \end{cases} \end{aligned} $$
其中,${\Theta}$ 第6个参数为表示目标合约的 gas
因此,[141] 的 Gas 为 2891423
--
推导3 $C_{\text{\tiny CALL}}(\boldsymbol{\sigma}, \boldsymbol{\mu}) = 2891523$
最后根据公式
$$ C{\text{\tiny CALL}}(\boldsymbol{\sigma}, \boldsymbol{\mu}) \equiv C{\text{\tiny GASCAP}}(\boldsymbol{\sigma}, \boldsymbol{\mu}) + C_{\text{\tiny EXTRA}}(\boldsymbol{\sigma}, \boldsymbol{\mu}) $$
因此,[140] 的 GasCost 为 $C_{\text{\tiny CALL}}(\boldsymbol{\sigma}, \boldsymbol{\mu}) = 2891423 + 100 = 2891523$
小结
理解上面的例子,应该就可以理解问题一和问题二了
至于问题三,为什么修改原题,加大 CALL 首个参数后题解无效?可以看看 $C_{\text{\tiny GASCAP}}$ 中的 min
最后,此前的题解利用 EIP-2929: Gas cost increases for state access opcodes 的方式比较非主流,正经解答请参考官方题解~
最后的最后,可以思考下,假设当时题目首个参数确实为比较大的值,那么能否仍然利用 EIP-2929 解题呢?// 一时挖坑一时爽
- 以太坊黄皮书学习笔记 6203 浏览

