突破区块链不可能三角(一) — 扩容,扩展,与无限扩展
- maxdeath
- 发布于 2020-01-17 10:42
- 阅读 8170
本系列详细地解释扩容和区块链不可能三角
本系列文章如下:
- 扩容,扩展,与无限扩展
- 在比特币POW之上的尝试
- POS与POW-DAG
- 区块链中的BFT及HotStuff BFT(Libra BFT)分析
- 闪电网络,链下技术,以及它们的局限性
- 吹个关于区块链活性的哨子
- 分片(上)
- 分片(中)
- 分片(下)
写在前面的话:
算是想了很久,加上个人最近工作上的变动,这篇又拖了很久,犹豫再三,决定这篇结合我自己的研究,来写一写区块链领域的热门问题——扩容和区块链不可能三角。
我看过不少介绍可扩展性和不可能三角的文章,中文和英文都有,甚至不乏一些知名作者或者著名研究机构的文章,但是没有一篇能够非常准确的完全解释清楚这个问题。不太客气地说,几乎每篇文章里总会有那么几句话会让我皱起眉头:“等等这里写得不对”。所以,我决定在这里用一个系列详细地解释这个问题。
那么,凭什么这篇会比其他的好一些呢?
实际上,区块链可扩展性,也就是不可能三角的这个问题,是我之前研究的主要方向,也是我一直想要写的东西。但是,具体到成文其实我斟酌了很久。犹豫的主要原因是,我个人其实比较抵触在科普文章里夹私货这种行为——我的答案里我会尽量分清科普的部分和个人意见的部分,而如果我要写科普文章的话,我会写一些更中立更经过检验的内容,而尽量避免仍旧争议或未经过同行评议的创新性内容。而且,由于应该说在区块链这个领域目前的现状是——大部分搞科普和媒体的人对于区块链技术不够专业,而大部分专业的人多多少少都是利益相关方,于是这个专栏的定位是希望创造一个“没有利益相关的专业视角”的原创技术专栏,因此我一直在刻意去避免自己成为某个“利益相关方”而失去了科普的中立性(当然,这完全是个人选择问题,有些区块链从业者的科普也做得很好)。
基于以上的原因,我一直都没有在我的专栏里介绍关于我自己的研究和成果,一方面,之前的成果还有待完善,另一方面,我也担心介绍不成熟的论点有悖于这个专栏的定位。不过,最终还是考虑在现在把这个东西写出来的原因,主要是因为我的论文“VAPOR: a Value-Centric Blockchain that is Scale-out, Decentralized, and Flexible by Design”在刚刚结束的Financial Crypto 2019上正式发表,因此,我觉得现在我比较有底气来写一写关于不可能三角的问题,也介绍一下自己对于这个问题的解决方案。
为了证明自己确实在区块链可扩展性领域有一定的发言权,可能在这里还是需要介绍一下我的一些工作:
我关于区块链无限扩展的第一篇论文Implicit Consensus: Blockchain with Unbounded Throughput于2017年5月上传arxiv,算是最早的关于无限扩展(scale-out)的论文之一,如果说投稿的时间的话,其实比公认最早的无限扩展方案omniledger上传arxiv的时间还要早两天。不过其实这没有什么值得说的,因为它没有正式在学术会议或期刊上发表,而且,从现在看起来,确实想法不算很成熟,关于无限扩展的原因没有写到点上。这篇文章的另一个偏工程实现的版本,发表于IFIP Networking 2018,叫A Blockchain Consensus Protocol With Horizontal Scalability。
后来,我把这篇文章的共识部分抽象出来进行了更严谨的证明,并且提出了Spontaneous Sharding(自主分片)的概念并做了实验室的仿真证明无限扩展的可能性,即:A Scale-Out Blockchain for Value Transfer with Spontaneous Sharding。这篇论文发表在Crypto Valley Conference on Blockchain Technology 2018上,这个会议据称(主办方说的)是IEEE的第一个区块链会议,虽然是个新会议,影响力远不及相关领域的顶会,名字听起来也很山寨,但是这个会确实是个正经的学术会议,审稿也很严格,技术委员会看起来简直是全明星阵容(主席包括康奈尔大学的Emin Gun Sirer教授),这也是我当时投这个会的原因。
我去年下半年的主要工作就是把这个共识算法可以达到无限扩展的原因再次抽象出来,并且针对这个原因提出了“价值中心区块链(Value-centric Blockchain)”的概念和理论结构,并且论证了这种结构实际上在实现“价值转移”,换句话说就是虚拟货币的基本功能上,比传统区块链的结构拥有许多优势,最重要的是,应该天然是无限扩展的。这篇论文最终在去年年底被Financial Cryptography and Data Security 2019(FC2019)接收,并且在今年二月20号发表了,就是上文中提到的那一篇。
在这里我说一下FC。关于FC,也许非密码学专业甚至非应用密码学领域的人听起来都有些陌生,在中科院的排名也只是C类(我是后来才知道还有中科院排名这回事。。。)。但是,这个会议在应用密码学领域,本就是声望卓著的顶会之一。而如果要具体到“区块链”这个刚刚出现在学术界没多久的领域的话,那么FC应该毫无疑问的是区块链领域的顶会。这其中有两个原因,一是历史原因:FC是最早开始接受关于比特币和区块链论文的会议之一,也是最早加入了比特币workshop的会议(相比于这两年陆陆续续的有不少相关领域的会议加入了关于区块链的workshop,FC早在2014年就加入了Bitcoin Workshop),许多关于比特币的重要论文都发表在这个会或者是BW上,例如selfish mining的论文,共识算法Ghost的论文,关于可扩展性的position paper:On scaling decentralized blockchain等等。这其中更深层次的原因是因为这个会的参会者的研究领域本来就与数字货币高度重合,所以这些人也成为了第一批学术界中接纳并开始研究比特币的学者,到了今年,由于区块链的热度已经上升成为金融密码学领域最热门的研究问题,以及其实际上已经无法界定哪些论文应该发表在主会而哪些应该发表在BW中,因此,主办方今年将BW并入了主会。第二个原因其实也和第一个原因相辅相成——到目前为止,FC(以及BW)的技术委员会都可以说是世界上最懂区块链的那批人,而也正是因此,对于一篇关于区块链的论文而言,FC是能够收到最客观和最有意义的审稿人意见的会议,同时,也是在区块链上的学术贡献最容易被发现和认可的地方。
这个是FC2019的网站:Financial Cryptography 2019
回归正题:扩容(Scaling)与扩展(Scaling)与可扩展的(Scalable)与可扩展性(Scalability)
以上这几个概念毫无疑问都是区块链领域的热词,但是,如果你是一个严谨的学者,或者,你只是喜欢刨根问底,想要真正从媒体或者白皮书乃至论文里想要搞清楚频繁出现的Scalability和Scaling到底是个什么意思,我估计你八成会被搞疯,因为很多论文里面说的scaling根本就不是一个事。但如果你恰巧又不是英文读者的话,那么这种混乱也许会被加剧,因为scaling在不同的语境下也许会被翻成扩容或扩展。总之,标题里提到的这三个词在区块链领域没有任何确切的定义,在不同的语境中他们可能有不同的意义,甚至,在有些白皮书中这个词可能没有任何意义。换句话说,当你在白皮书上看到“这是个可扩展的区块链”或者“解决了可扩展性问题”又或者“可扩展的共识算法”的时候,在不结合上下文的情况下,你压根就不知道它指的是什么。
出现这种情况的原因,我认为,是因为区块链本身就是个没有严谨定义的领域,而Scalability在各领域中又有不一样的定义,因此,当不同领域的人来按照自己的想法定义Scalability的问题,而没有一篇共同承认的权威论文或者教材做出某个大家都认可的定义时,就变成了现在这个样子——人人都可以从自己的角度上去说自己的系统是可扩展的。而接下来,由于大部分人都很难理解这些不同方案之间关于可扩展性的区别,于是,很多概述文、科普文、媒体文将各种可扩展混为一谈就更加剧了这种混乱。
可扩展的第一个定义——可扩展的POW
我们来先说说什么是scalable(可扩展的)。在不加任何限定下,这是指某个表现x随着某个变量y的增长的变化情况,如果x能够随着y的增长而线性增长,我们会说x是linear scalable的,或者就简单地说是scalable的。换句话说,如果我们定一个很高的目标x,如果我们知道“这种东西我们只要用某f方法,然后把y堆起来就一定可以达到”,那么我们就说这个f方法是scalable的。
然后,在很早之前,人们就已经意识到比特币是不scalable的——因为想要提升比特币的7TPS,尤其是想要把它提高到能和传统支付手段相比的输出,例如10000TPS,我们能做的事很有限。最自然而然的方法是加大区块大小,或者降低区块间隔,而因为即便没有严谨的数学分析和证明,人们也知道这是不可能的,因为要是把区块加大1000倍到一个G然后十分钟一个区块,不说别的,就是放在当时的网速也不允许。
然而,其实制约区块大小和区块间隔的远远不止传输区块的网速。定量的分析大家可以参照前文提到的On Scaling Decentralized Blockchain那篇论文,而定性的解释是——
比特币的POW算法里,安全性依赖于区块同步速度远小于区块间隔的前提。
比特币的安全性的前提是——假设所有矿工都是逐利的,那么任何人想要作弊,都需要打败50%的算力,因为你必须要拥有超过其他人的算力,才能挖出比别人更长的链。然而,这个竞争是公平的前提是,作弊者和其他所有人都在挖同一条链,即全网对于当前最长链在大多数时间里是同步的。然而,对于比特币而言,这是不一定的。而这也是比特币的POW和传统分布式系统的算法不一样的地方——比特币中允许网络中出现短暂的不一致,即分叉,即网络中的两部分不同节点同时分别认为两条不同的链是合法的。这个时候,如果恶意节点想要挖出最长的链,他不再需要竞争过其他所有人了。假设一个分叉中两条链各被50%的算力接受,那么这个时候一个恶意节点只要拥有超过25%的算力就能够有超过50%的概率挖到下一个区块了。于是,如果比特币中总是拥有两条分叉,我们其实可以认为比特币的安全性下降了一半。
看到这里也许大家还不理解——比特币不是很少出现分叉,而且一般分叉很快就会消失吗?为什么会有“比特币中多数时间都在分叉”的情况出现呢?
这里,大家来回想一下分叉是怎么出现的——当A挖到一个块的时候,A会尽快把这个块公布到全网,越多的人知道,就越多人会继续在后面挖矿,于是这一条链比别人长的可能性就越大,于是这一块最终出现在最长链上的可能性就越高——而在比特币中,只有最长链上的才是最终结果。然而,如果A的这块还没有被网络中的另一点B收到的时候,B也挖到了一块,而B在不知道A挖到这块的前提下,也会做同样的事情,于是就产生了分叉,而网络也会被分割成两部分,先收到A的块的就会认为A的链更有前途,在后面继续挖,反之亦然。在现在的比特币网络中,一个区块是1M,传输和验证起来都比较快,所以需要把一个区块同步到全网的时间很短,只有当两个节点在这段时间里同时挖到区块才可能产生分叉。因此,如果这个延迟远小于区块间隔的话,分叉的概率就会很小,而连续几次分叉的概率就更小,所以大概率分叉在一个区块后就会结束,留下一个深度1的孤块。而如果我们加大区块大小,或者缩短区块间隔,使得同步区块的时间和区块间隔的比例没有那么悬殊的时候那么同步所需要的时间就会变长,于是产生分叉的可能性就会增加。而如果同步区块时间超过了区块间隔,那么分叉数量就永远不会减少,而是会越来越多。
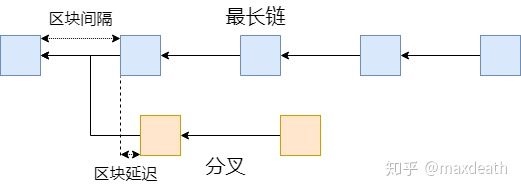
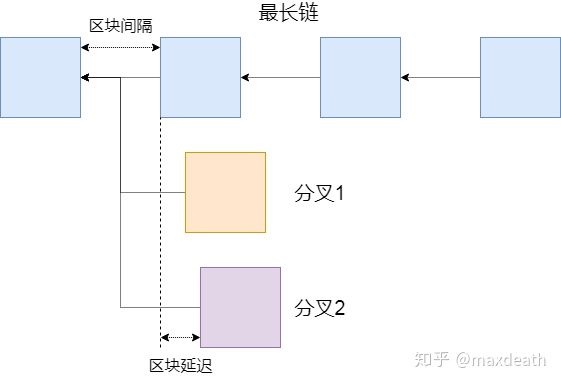 区块大小增大导致区块传输延迟增大,于是区块延迟/区块间隔的比例增大导致网络中可能出现分叉的几率增大。同理,如果减小区块间隔也会造成一样的结果。
区块大小增大导致区块传输延迟增大,于是区块延迟/区块间隔的比例增大导致网络中可能出现分叉的几率增大。同理,如果减小区块间隔也会造成一样的结果。
而如果网络中一直有分叉,很难收敛,那么就总有人不是在最终的最长链上挖矿,于是整个网络的安全性就达不到POW理论上的50%的水平;而分叉无法收敛,则不仅仅是安全性下降,而是交易永远无法确认。
后者不仅仅局限于比特币的POW算法,而可以说是区块链不可能三角或者说分布式系统CAP的问题——如果网速跟不上区块传播速度,无论如何这个系统是不可能保证一致的。
但前者,则是比特币POW算法上的限制。
从这个角度讲,比特币不可扩展——因为它的输出不能随着扩大区块大小(减小区块间隔)而在碰上网速的边界之前无限提升,而是在那之前就先碰上比特币POW算法自身安全性对于同步依赖的边界了。
于是,也是出于同样的角度,我们想要改进比特币的POW算法,使得它能够摆脱安全性对于同步性的依赖,使得我们能够简单地通过扩大区块大小(减小区块间隔)来提升输出,直到遇到网速的边界为止,这类的尝试,我们称为“扩展比特币(Scaling Bitcoin)”,而这样的算法,则可以称为“可扩展的POW算法”,因为,相比于比特币的POW,它们从这个角度上来讲更可扩展了。
这一类算法例如Bitcoin-NG,GHOST,Hybrid Consensus等。然后,可扩展性也在同一级别的还包括使用了类比特币POW结构的POS例如Snow White和Ouroboros,我们下期再详细介绍。
可扩展的第二个定义——无限扩展
看到这里,可扩展的定义似乎没什么争议——实际上,一开始当没有区块链只有比特币的时候,谈到可扩展,就是第一个定义。
那什么时候开始“可扩展”这个词又有了新的意思呢?
大概是从传统分布式系统的人开始研究比特币开始的……
在传统分布式系统里,通常scalable的定义是指系统的输出是否能够随着增加节点的数量而线性增加,如果能,就是scalable的,或者叫Horizontally scalable的。所以用这个定义的话,如果一个区块链系统是scalable的,那么如果他有1000个节点的输出是x,那么如果我们加上1000个节点,输出应该变成2x。比如,如果把比特币的网络扩大一倍,那么TPS应该翻倍。
然而,如上所述,比特币并没有这样的性质——比特币的算法决定了它的输出就是7TPS。
因此,比特币是不scalable的。
但是,其实这带来了一个问题——从这个角度讲,就算是第一个定义中可扩展的POW也不是scalable的,即便到现在为止,也几乎没有哪个区块链是scalable的,其实这也好理解——一个linear scalable的分布式系统中,每增加一台服务器它都能增加相应的输出的原因是,新增加的这台服务器可以独立承担一部分任务。
而区块链和传统数据库不同,它几乎一定在某种程度上需要多个节点存储同样的数据(传统分布式数据库的人管这叫异地多活,冗余设计),否则就失去了去中心的意义,所以,一定从某种程度上,它无法达到多出几个节点就提高多少输出的效果。除非,它要做出一定的安全性牺牲,或者可信假设,而这就是总是被人津津乐道的“区块链不可能三角”。
因此,很多人诟病对于这种scalable的追求——他们认为牺牲了安全性和去中心化而盲目追求高输出,就失去了区块链的意义。
然而,即便如此,高输出的吸引力还是巨大的——区块链出现之后,人们总是把区块链对标互联网,也总是把公链对标未来的互联网独角兽。然而,如果区块链达不到这样的可扩展性,那么它的输出最终会受制于网络,是无论如何支撑不起互联网独角兽的场景的。为了将这种可扩展和之前所说的可扩展区分开,在区块链共识算法的语境下,这种被称为scale-out,即无限扩展。
总体来说,能够达到无限扩展目前的方法有两类——链下技术和分片,前者其实本身就不在不可能三角的框架之中,从我的角度看,更多的是一种把区块链当成可信中介,然后根据不同应用和场景,然后考虑不同区块链的特性,提出一个可以借由区块链的链下解决方案。例如链下支付通道,实际上就是储值卡这种针对小额高频交易的解决方案在区块链场景中的映射。从理论上来讲,链下技术和链上最大的区别在于BFT中的一致性(见上一篇),链上技术需要共识算法保证交易的一致性(尽管可能会需要在安全性或者去中心上做出妥协),而链下技术中交易的一致性共识算法本身是不管的,而依赖于链下方案本身的设计以及双方根据场景对链下的协商。
但是,在学术界,通常不用scale-out这个词来形容链下算法——因为就如我之前说的,链下算法天然scale-out,所以没有必要再特地去用这个词来形容。所以,一般说道scale-out都是分片算法,能够归于这一类的算法包括Omniledger,Chainspace,和 @王嘉平老师的Monoxide,以及偏工程的以太坊分片和Rchain,我的方案VAPOR从结果看来也是分片,但是原理比较不同。这些,我最后一部分再详述。
从这种角度看来,两者似乎和很火的另外两个概念即“第二层(链下扩容)”和“第一层(链上扩容)”方案的定义非常类似,但是实际上,第一层和第二层的概念更多地不是从我们在这里考虑的无限扩展角度出发的,而是从“要不要改变主链算法”或者“是不是通过链上抵押把交易挪到链下进行”这种角度定义的,所以,实际上,除了分片,许多达不到“无限扩展”而只是“可扩展”,即我们的第一个定义以及我们接下来要讲的第三个定义的方案,也被称为第一层方案。
这其中,最容易造成混淆的是DAG(有向无环图)。由于一些DAG项目的宣传,以及很多人对于DAG结构直观印象造成的错误概念,DAG在很多综述类文章中被和分片并列,认为是无限扩展的——然而,DAG只是一个概念,而把DAG用于区块链的方法有很多,例如GHOST,BLOCKDAG,SPECTRE,PHANTOM,Swirld Hashgraph,IOTA,Byteball,Conflux等等。尽管DAG理论上有无限扩展的可能,但是目前的所有有具体算法的DAG方案(光有个概念的不算)中,没有一个是无限扩展的,而都只是可扩展。
可扩展的第三个定义——可扩展的BFT
现在,如果管第一类的可扩展叫做“可扩展”,第二类叫做“无限扩展”,似乎“可扩展”这个词也没有什么歧义。
然而,实际上我们还有第三个概念,就是我之前介绍过的BFT类算法。
之前我的几篇文章中着重介绍了拜占庭容错问题和一些重要的拜占庭容错算法,其中,我们介绍了一个重要的拜占庭容错算法PBFT(实用拜占庭容错),也介绍了它的消息复杂度是O(N^2),即,想要对一条消息(一笔交易)达成共识,需要首先将消息广播给网络中的每一个节点(O(N)消息复杂度),然后为了防止恶意节点伙同恶意消息发布者故意在网络中散播假消息导致不一致,每一个节点需要再把自己收到的消息广播一遍,于是就有了O(N^2)的消息复杂度。
O(N^2)是个什么概念呢?我们用可扩展性的概念去分析一下——假设每个节点的带宽是c,那么全网的总吞吐量上限是cN。那么,消息复杂度是O(N^2)的概念是,如果你把节点数量翻一倍,那么全网的带宽变成原来的两倍,但是所需要消耗的资源却是原来的四倍。换句话说,传统BFT岂止是不可扩展,简直是可扩展的反面,所以采用BFT算法的区块链的共识节点基本上都只有十几或者几十个。
而我在之前关于BFT的文章里也说过了,大家一开始并没有认为这个O(N^2)消息复杂度有啥问题,因为第一,他们一开始没考虑实用,第二,就算有了PBFT,也只是考虑在安全条件更严苛分布式数据库中使用,并没有考虑到区块链这种大网络的场景。
然而,当区块链出现之后,人们又开始重新审视BFT的时候,O(N^2)消息复杂度就完全没法用了。于是,人们开始考虑更“可扩展”(你看,又是这个词)的BFT算法,即O(N)消息复杂度的BFT算法,这类BFT算法就多了,包括Honeybadger,Byzcoin,Hyperledger-Iroha,Elastico,乃至Algorand和Avalanche的BFT的部分,都属于此类。他们确实是“使用了(更)可扩展的BFT的区块链”,然而,当有的地方单纯地在突出他们的优势的时候说“可扩展”或者简单地把他们称为“可扩展的区块链”的时候,就和第一类可扩展的POW混在一起了。虽然,我们会在后面介绍,两者实际上最终的效果是殊途同归的。但是,如果想要更深刻的理解这个问题,需要知道可扩展的POW和可扩展的BFT的来历并不一样。
可扩展的第3.5个定义——比特币扩容
此外,还有第3.5类可扩展,也就是比特币扩容方案——例如大区块和隔离见证。
之所以是第3.5类,是因为从任何角度来讲,它们都只是提高了一些输出,而完全没有解决可扩展性问题。然而,扩容本身英文也是scalable,而且从历史角度讲,这两个方案的确也是扩展的第一步,因为——
大区块-->分叉多-->采用GHOST-->可扩展POW
隔离见证-->解决比特币可变性问题-->方便链下方案的实现-->无限扩展
所以,从这种角度讲,说两个方案扩展了比特币也无可厚非——只不过最终,真正在比特币上的升级,也就只停留在了这第一步上。
不同定义之间的关系
看到这里,是不是很多原先以为自己已经了解了可扩展性问题的人觉得脑子更乱了——
难道想知道什么是可扩展的区块链就一定得知道这东西的来历么?有没有啥可以更简单的可以在一看到“可扩展的区块链”,就知道它大概是做什么的,它的性能是什么的方法呢?
实际上很简单——
首先,第3.5类只有两种方案,大区块和隔离见证首先可以排除出去,因为这两种方案现在基本上只会以“扩容”的名称出现,只有非常不专业的地方会用“可扩展”的名义去拿它和其他可扩展算法比较。
其次,在目前,能标榜自己是“无限扩展”的,基本上也不会介绍自己是“可扩展”的。如果这里仍有疑问的话,也只要记住,分片和链下技术是不应该和其他“可扩展”方案放在一起比较的,因为这两个方案的可扩展性更高,即在大网络中的输出更高,但是会在安全性或者中心化上做出一些妥协。更基础一些的不同是——看这些算法为了保证一致性,是不是要求每个节点都记录每一笔交易,如果是,则消息复杂度至少是O(N),于是当网络中加入节点的时候,输出一定是不会增加的。而想要无限扩展,就一定有一些交易,是不需要广播到整个网络的。
然后,剩下的所有可扩展算法,即我们定义中的第一种和第三种,其实最终都殊途同归,达到了一样的可扩展性,即O(N)消息复杂度。然后,两者的输出最终都只会受到网络网速和响应延迟的约束,最终,比较优秀的算法大概在实验室环境下,达到1000TPS这个量级,最终当然还是会取决于算法的优劣以及实现的优化程度,但是实验室环境模拟的大网络的延迟实际上是远好于实际的水平,所以在现实中,随着网络的扩大,输出不随着节点数量增加的提升而提升是个美好的想象——输出几乎一定会随着网络的增大而下降。
这其中最容易混淆的就是DAG,但是这类算法中,我们之前也已经介绍过了,无论是工业界的IOTA,Swirld Hashgraph还是偏学术的Phantom和Conflux,无论在某些媒体或,文章,或者他们自己白皮书中是怎么介绍的,请记住,它们严格都是“可扩展”的共识算法,而不是“无限扩展”的。
下一篇:比特币的尝试,我们会着重介绍这里第一种和第三种定义中的可扩展方案,他们的共性和目前面临的挑战。在后面,我们会介绍一些DAG算法和分片的算法,最后介绍一下我自己的工作。这次,我会尽量地更新的快一些……
