zk-stark实践
- jianghai
- 发布于 2022-06-07 11:20
- 阅读 6636
zk-stark意为零知识—可拓展的—透明的—知识论证,在区块链上的应用前景备受瞩目。它不仅能提供隐私功能,还能提供无需信任第三方的扩容功能。下面将从一个具体问题出发对 zk-stark进行实践
目前 rollup已经成为ETH链下扩容的主流,rollup可以分为 op-rollup和 zk-rollup。其中 op-rollup基于经济学方法解决信任问题;而 zk-rollup基于数学方法解决信任问题,被认为是一种终局性的解决方案。
zk-rollup又可以分为两种方案,zk-snark和 zk-stark。两者都将待证明程序执行转换为证明多项式存在特定根式。而对多项式存在特定根式的证明,前者通过在 ECC加密空间进行挑战—证明的模式,再通过可信设置将交互模式转变为非交互模式;后者通过对原式除以根式后的式子进行低度测试进行证明。
zk-stark意为零知识—可拓展的—透明的—知识论证,在区块链上的应用前景备受瞩目。它不仅能提供隐私功能,还能提供无需信任第三方的扩容功能。下面将从一个具体问题出发对 zk-stark进行实践(本文来自于对V神关于zk-stark的三篇文章的实践与总结,文章链接见最后的引用)
背景知识
在正式开始前,可以先搞清楚一些背景知识;也可以先跳到下一章,到需要时再回过头看这一章。
模运算
模运算,即求余运算,使得运算发生在有限空间中。通过模运算,数学家们建立起一个新的运算系统,而且这个运算系统与传统数学运算系统是自洽的。我们可以在新的运算系统讨论传统系统里的各种结构,包括称为“常规数学”的多项式。而密码学家尤其喜欢这个新的运算系统。
模运算系统中同样有四则运算以及指数运算,不过它的除法运算实现起来比较复杂,一般是先求除数的逆元,将除法转换为乘法进行计算。
实际中,一般以质数 p为模:
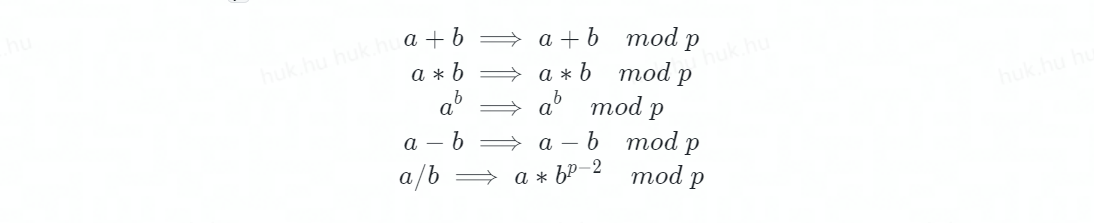
费马小定理
假如 a是一个整数,p是一个质数,那么 a^p-a是 p的倍数。
费马小定理也可以用来求逆元,这是模运算体系下除法运算的基础。
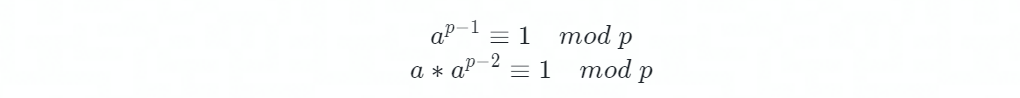
费马小定理还有个推论,在模运算空间中,若 p-1是 k的倍数,x => x^k的值空间的大小为 (p-1)/k+1
欧几里得拓展算法
欧几里得算法又叫辗转相除法,用来求两个数的最大公约数。对欧几里得算法进行拓展也可以用来求模运算下的逆元。
蒙哥马利算法
当在模运算中有除法时,会先通过逆元将所有的除法转化为乘法。不过求逆元的操作也很麻烦,当需要求大量逆元时,也很耗时。蒙哥马利算法通过将多个求逆元的操作转化为多个乘法以及一次求逆元的操作来简化计算:

快速傅里叶变换
在 zk-stark的计算过程中,有很多需要根据多项式系数求点值,以及根据点值求多项式系数的。使用拉格朗日插值法也可以计算,但其时间复杂度为 O(n^2),而快速傅里叶变化为 O(n*log(n))。例如若需要对100万个点进行插值,拉格朗日方法需要计算1万亿次,而快速傅里叶变换只需要2千万次。不过快速傅里叶变换对取点有要求,需要按等比递增,并且个数满足 2^k
低度测试—FRI算法
多项式的度指的是最高次数。假设已知一个多项式的 n个点,如何证明其度最高为 m呢(m<n-1,根据拉格朗日插值算法,n个点可以决定一个度最高为 n-1的多项式)。一个比较简单的方法是,先使用 m+1个点求出一个 m次多项式,然后验证其它点都在此多项式上。但当 m很大时,这种方法的计算量会线型增加。FRI算法可以以小于 m次的计算量验证上述问题。
思路如下。假设有 N(比如等于10亿)个点,位于一个度小于 m(等于100万)的多项式中。假设 f(x)=x^12012+x^11011+x^3005+x^1001+x+1,现在令 y=x^1000代入可得 g(x,y)=x^12*y^12+x^11*y^11+x^5*y^3+x*y+x+1。对于 g(x,y),固定 y不变时,对 x来说,多项式的度小于1000;同样的,固定 x不变时,对 y来说,多项式的度也是小于1000
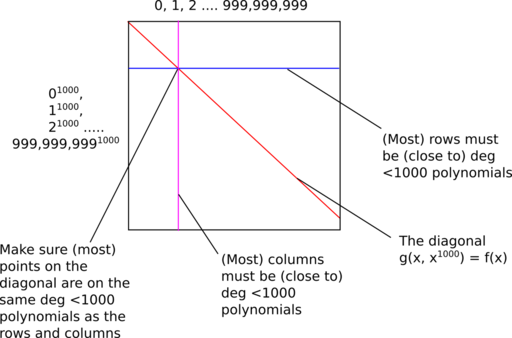
证明流程:
- 证明者首先需要计算
g(x,y)每行每列上所有点的值,需要计算10^18次,并得到其 Merkle Root - 验证者随机选出几十行和几十列,对于每一行或列,随机选择
1010个点,证明者还需要给出相应的 Merkle 路径,验证者验证 Merkle 路径以及其度是否小于1000
可以看到在这种情景下,证明者需要计算 10^18次,下面考虑如何减少证明者的计算。
前面提到,费马小定理有个推论,在模运算空间中,若 p-1是 k的倍数,x => x^k的值空间的大小为 (p-1)/k+1,且每个值对应 k个元素。所以事实上,证明者只需要计算 10^9次,对于上图中的某一行,相关的点可以在前面的计算中找到;而且某一行可以插值到指定列,这样就为列上的低度计算准备了数据。
新的证明流程:
- 证明者计算
f(x)所有点的值,需要计算10^9次,并得到其 Merkle Root - 验证者随机选择一些列,在每一列上随机选择一些点,点的值来源于对应行的插值,而对应行插值的数据源是证明者已经计算的
f(x)的值,同样证明者需要给出所有用到的点的 Merkle 路径
实际计算时,往往取 y=x^4,而 y的低度证明,再次使用 FRI方法,令 z=y^4,可以不断这样进行下去。

zk-stark证明思路
- 程序计算的每一步会对应一个值,所有的步骤组合起来形成一条计算轨迹,也对应一个多项式
P(n) - 计算轨迹的每一步计算产生一个约束
C(p)=0 - 将轨迹多项式与约束多项式多项式与约束多项式结合起来得到
D(x)=C(p(x),p(x-1)....) - 组合多项式
D(x)在计算轨迹的每一步处都为零,即具有根式Z(x)=(x-x_1)(x-x_2)...(x-x_n) - 使用
FRI算法对多项式T(x)=D(x)/Z(x)进行低度检验
待证明问题
def mimc(inp, steps, round_constants):
start_time = time.time()
for i in range(steps-1):
inp = (inp**3 + round_constants[i % len(round_constants)]) % modulus
print("MIMC computed in %.4f sec" % (time.time() - start_time))
return inpmimc函数的计算过程如下

说明
- 这里的计算是在有限域内的模运算,模取
2^256-351*2^32+1,为[1,2^256]范围内的最大质数,比特币和以太坊的相关计算也是以此数为模 round_constants的长度较小,在整个计算中循环使用,这里取64mimc算法只能依次进行,不能并行计算
问题证明
在使用zk-stark证明上述问题时,需要做一些说明
- 证明中需要大量的根据多项式的点值求系数以及系数求点值的计算,使用FFT(快速傅里叶变换)算法;
- FFT算法对点的数量和位置有要求,需要点的数量为
2^n,并且x坐标依次具有等比关系; - 原本轨迹多项式的自变量
x取值为自然数序列,这里取某一质数的对应的幂,即x'=p^x,来满足FFT算法对点x位置的要求; - 当轨迹多项式的样本点不满足
2^n时,需要补充,相应的值可以取0 - 在证明时,需要对原本的样本点进行延拓,也就是需要插值。对有限域里面的幂进行插值,需要针对单位根做文章。假设原本的单位根为
G1,现在需要拓展k倍,则令新的单位根为G2, G1=G2^k,即可满足要求
下面对生成zk-stark的证明的mk_mimc_proof做进一步的说明
- 首先,是一些
assert函数
assert steps <= 2**32 // extension_factor
assert is_a_power_of_2(steps) and is_a_power_of_2(len(round_constants))
assert len(round_constants) < steps拓展因子是用来对原本的执行轨迹的点做插值的
- 然后是计算轨迹在每一步的值
# Generate the computational trace
computational_trace = [inp]
for i in range(steps-1):
computational_trace.append(
(computational_trace[-1]**3 + round_constants[i % len(round_constants)]) % modulus
)
output = computational_trace[-1]
print('Done generating computational trace')- 然后是在原本的轨迹点处进行插值拓展
# Interpolate the computational trace into a polynomial P, with each step
# along a successive power of G1
computational_trace_polynomial = fft(computational_trace, modulus, G1, inv=True)
p_evaluations = fft(computational_trace_polynomial, modulus, G2)
print('Converted computational steps into a polynomial and low-degree extended it')这里,先基于原本的单位根 G1使用反向FFT计算多项式系数,然后基于新的“更小的”单位根 G2使用FFT计算点值
- 然后是拓展并获取循环常量的表达式
skips2 = steps // len(round_constants)
constants_mini_polynomial = fft(round_constants, modulus, f.exp(G1, skips2), inv=True)
constants_polynomial = [0 if i % skips2 else constants_mini_polynomial[i//skips2] for i in range(steps)]
constants_mini_extension = fft(constants_mini_polynomial, modulus, f.exp(G2, skips2))
print('Converted round constants into a polynomial and low-degree extended it')- 然后是构造组合多项式
# Create the composed polynomial such that
# C(P(x), P(g1*x), K(x)) = P(g1*x) - P(x)**3 - K(x)
c_of_p_evaluations = [(p_evaluations[(i+extension_factor)%precision] -
f.exp(p_evaluations[i], 3) -
constants_mini_extension[i % len(constants_mini_extension)])
% modulus for i in range(precision)]
print('Computed C(P, K) polynomial')- 然后是计算需要进行
FRI检验的数据
# Compute D(x) = C(P(x), P(g1*x), K(x)) / Z(x)
# Z(x) = (x^steps - 1) / (x - x_atlast_step)
z_num_evaluations = [xs[(i * steps) % precision] - 1 for i in range(precision)]
z_num_inv = f.multi_inv(z_num_evaluations)
z_den_evaluations = [xs[i] - last_step_position for i in range(precision)]
d_evaluations = [cp * zd * zni % modulus for cp, zd, zni in zip(c_of_p_evaluations, z_den_evaluations, z_num_inv)]
print('Computed D polynomial')注意 Z(x)=(x-x_1)(x-x_2)...(x-x_n),在此处,等于 (x^steps - 1) / (x - x_atlast_step)
- 对输入输出单独处理
# Compute interpolant of ((1, input), (x_atlast_step, output))
interpolant = f.lagrange_interp_2([1, last_step_position], [inp, output])
i_evaluations = [f.eval_poly_at(interpolant, x) for x in xs]
zeropoly2 = f.mul_polys([-1, 1], [-last_step_position, 1])
inv_z2_evaluations = f.multi_inv([f.eval_poly_at(zeropoly2, x) for x in xs])
b_evaluations = [((p - i) * invq) % modulus for p, i, invq in zip(p_evaluations, i_evaluations, inv_z2_evaluations)]
print('Computed B polynomial')为了对输入输出的值进行证明,首先根据输入输出得到一条曲线,然后使用原来的曲线减去刚得到的曲线,得到新曲线,则将输入输出的信息包含在曲线中
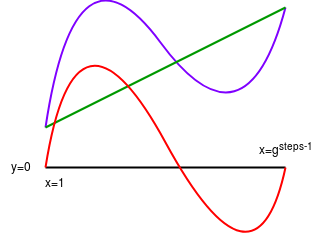
- 减少FRI算法的证明量
# Compute their Merkle root
mtree = merkelize([pval.to_bytes(32, 'big') +
dval.to_bytes(32, 'big') +
bval.to_bytes(32, 'big') for
pval, dval, bval in zip(p_evaluations, d_evaluations, b_evaluations)])
print('Computed hash root')
# Based on the hashes of P, D and B, we select a random linear combination
# of P * x^steps, P, B * x^steps, B and D, and prove the low-degreeness of that,
# instead of proving the low-degreeness of P, B and D separately
k1 = int.from_bytes(blake(mtree[1] + b'\x01'), 'big')
k2 = int.from_bytes(blake(mtree[1] + b'\x02'), 'big')
k3 = int.from_bytes(blake(mtree[1] + b'\x03'), 'big')
k4 = int.from_bytes(blake(mtree[1] + b'\x04'), 'big')
# Compute the linear combination. We don't even both calculating it in
# coefficient form; we just compute the evaluations
G2_to_the_steps = f.exp(G2, steps)
powers = [1]
for i in range(1, precision):
powers.append(powers[-1] * G2_to_the_steps % modulus)
l_evaluations = [(d_evaluations[i] +
p_evaluations[i] * k1 + p_evaluations[i] * k2 * powers[i] +
b_evaluations[i] * k3 + b_evaluations[i] * powers[i] * k4) % modulus
for i in range(precision)]
l_mtree = merkelize(l_evaluations)
print('Computed random linear combination')将前面的 P,D,B使用他们的 merkle root进行伪随机线性组合,则只需要对组合后的数据进行 FRI低度检测,该组合的次数小于 2*steps
- 生成随机索引,并提供相应的默克尔分支以及证明
# Do some spot checks of the Merkle tree at pseudo-random coordinates, excluding
# multiples of `extension_factor`
branches = []
samples = spot_check_security_factor
positions = get_pseudorandom_indices(l_mtree[1], precision, samples,
exclude_multiples_of=extension_factor)
augmented_positions = sum([[x, (x + skips) % precision] for x in positions], [])
#for pos in positions:
# branches.append(mk_branch(mtree, pos))
# branches.append(mk_branch(mtree, (pos + skips) % precision))
# branches.append(mk_branch(l_mtree, pos))
print('Computed %d spot checks' % samples)
# Return the Merkle roots of P and D, the spot check Merkle proofs,
# and low-degree proofs of P and D
o = [mtree[1],
l_mtree[1],
mk_multi_branch(mtree, augmented_positions),
mk_multi_branch(l_mtree, positions),
prove_low_degree(l_evaluations, G2, steps * 2, modulus, exclude_multiples_of=extension_factor)]
print("STARK computed in %.4f sec" % (time.time() - start_time))
return o至此,证明就结束了。而验证过程则是反着的,先是解析数据;然后验证默克尔路径;然后检查 C(P(x), P(g1*x), K(x)) = Z(x) * D(x)、B(x) * Z2(x) + I(x) = P(x)以及线性组合,并进行 FRI低度检验
链接
STARKs, Part I: Proofs with Polynomials
- ZK编年史:哈希登场 147 浏览
- Layer Zero 发布 Zero 链:去中心化的多核世界计算机 359 浏览
- “Jolt Inside” - 构建者需要了解的全新武器 286 浏览
- 以太坊的下一个重大转变:从重新执行每笔交易到验证 ZK 证明 372 浏览
- Zcash:比特币遗忘的隐私 432 浏览
- ZK编年史:计算模型 301 浏览
- lambdaworks 2026 年更新路线图和优先级 365 浏览
- 2026年构建机构级DeFi平台真正需要什么 907 浏览
- zkMesh:2026年1月回顾 450 浏览
- 如果它能编译,那它就是正确的(几乎):Lean 4 在 ZK 系统和工程中的介绍 644 浏览
- Zcash 的时代到来了 779 浏览
- ZK 编年史:电路(第二部分) 422 浏览

