《编程珠玑》第二章提到了两个问题，解法都非常精妙，展示了二分搜索和排序等基本操作获得高效算法的威力。

编程珠玑:Rust实现“无处不在的二分搜索”问题

问题描述及思路

给定一个最多包含40亿个随机排列的32位整数的顺序文件，找出一个不在文件中的32位整数（在文件中至少缺失一个这样的数—为什么？）。在具有足够内存的情况下，如何解决该问题？如果有几个外部的“临时”文件可用，但是仅有几百字节的内存，又该如何解决该问题？

第一个精妙的算法是第一张提到的位图排序算法：如果有足够的内存， 可以采用书中第1章中介绍的位图技术，使用536 870 912个8位字节形成位图来表示已看到的整数，将已知的整数对应的位置为1，然后从高位依次搜索该位图的每一位，为0的一位对应的整数即为所求，算法复杂度O(n)。

在内存不够时，位图和对所有整数排序的操作都不可行，作者提到了一个非常精妙的二分搜索实现算法。

其基本思想是根据元素的二进制位为0或1来进行二分查找。具体而言：根据整数的最高二进制位是否为1，将所有数据中该位为0的划到左半部分(记为:l),为1的划到右半部分(记为:r),由于数据有缺失，因此该数据肯定在长度更小的那一部分中(记为arr= l if l.len()< r else r)；然后在arr中重复上述操作，直到l或r的长度为0，就说明这个整数不存在。

举一个简单例子，假设最多包含7个整数的3位整数文件(arr)，其中缺失的整数为4，那么算法流程如下:

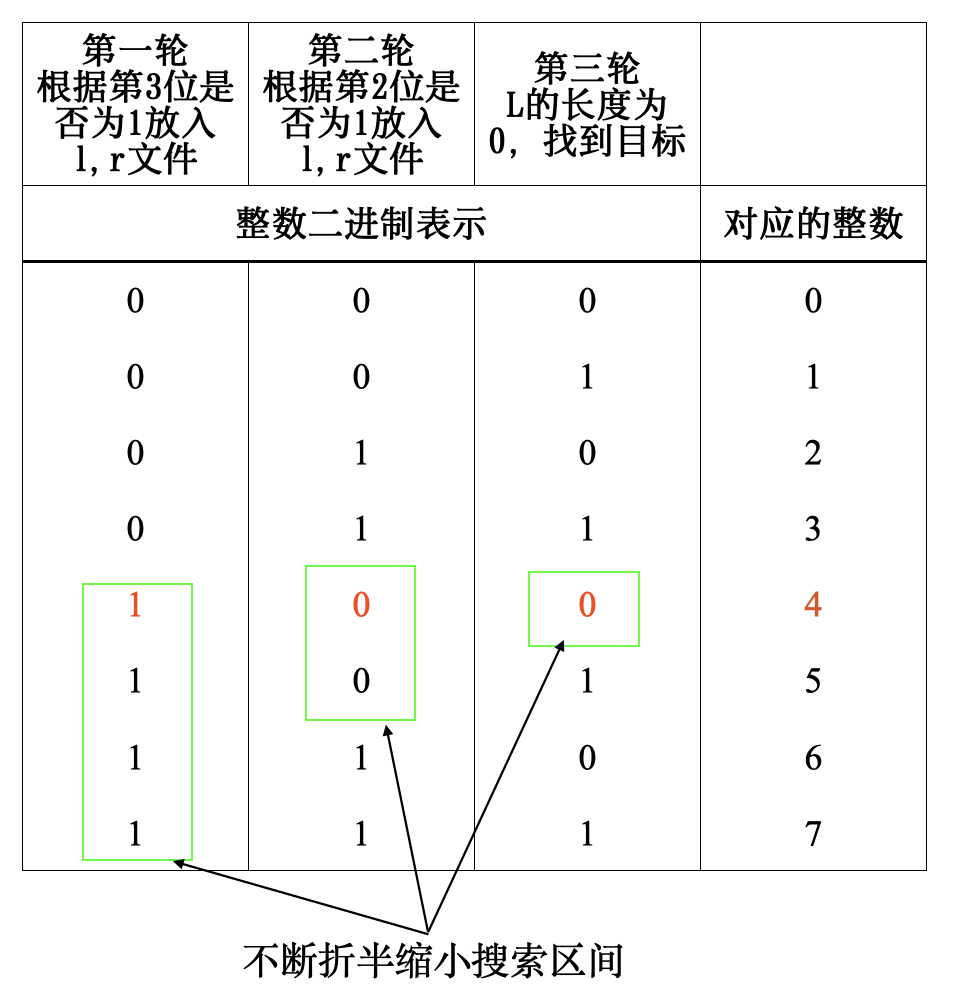
1. 第一轮 elem & 1<<2 ;for elem in arr 则l=[0,1,2,3], r=[5,6,7]，由于r中元素的个数更小，因此缺失的数据肯定在r中，且该元素第2为肯定为1。令arr=r,继续下一轮操作;
2. 第二轮 elem & 1<<1 ;for elem in arr 则l=[5],r=[6,7],同理缺失的数据在l中，且该元素第1为为0。令arr=l，继续下一轮操作;
3. 第三轮 elem & 1<<0 ;for elem in arr 则l=[],r=[5],由于l中元素个数位0,因此l对应位上的整数即为缺失的数据，且该元素第0位肯定为0。 因此缺失的数据为: 1<<2 + 0 + 0 = 4

Rust代码实现

fn search_miss(files: &[u32],bit:i32) -> u32 { //用files模拟包含40亿个随机排列的32位整数的顺序文件
    let mut bit = bit;
    let mut arr = Vec::from(files);
    let mut res = 0;
    let mut l:Vec<u32> = vec![];  //这里用Vec模拟外部可用的“临时”文件
    let mut r:Vec<u32>= vec![];   //这里用Vec模拟外部可用的“临时”文件
    while bit >= 0 {
        // looping invirant: 1. bit > 0 2. thre result located in the array whose length is smaller
        // breaking condition: one arr‘s length is zero
        for index in 0..arr.len(){
            let elem = arr[index];
            if elem & (1<< bit) == 0  {
                l.push(elem);
            } else {
                r.push(elem);
            }
        }

        if l.len() <= r.len() {
            arr = l.clone();
        } else {
            arr = r.clone();
            res += 1<<bit;
        }

        if l.len() == 0 || r.len() == 0{
            break
        }
        l.clear();
        r.clear();
        bit -= 1;
    }
    res
}

fn main(){
    //scanfoidding to create random array inputs
    let mut arr = vec![];
    let bit = 16;
    for i in 0..1<<bit{
        arr.push(i);
    }
    arr.remove((1<<10)+1);
    arr.remove(1<<9);
    arr.remove(1<<5);
    // thread_rng().shuffle(&mut arr);
    println!("res:{:b}", search_miss( &arr,bit -1));
}

编程珠玑:Rust实现“变位词”问题

问题描述及思路

一个变位词问题,该问题非常巧妙地使用排序这一基本操作来进行预处理，非常精妙: 给定一个英语字典，找出其中的所有变位词集合。 例如，“pots”、“stop”和“tops”互为变位词，因为每一个单词都可以通过改变其他单词中字母的顺序来得到。 例如:

输入:
["pans","pots","opt","snap","stop","tops"]
输出:
[
    ["pans","snap"] 
    ["pots","stop","tops"]
    ["opt"] 
]

对于该问题，任何采用排列组合的方法来生成所有可能得单词组合方法都会失效，比如22个字符长度的单词的变位词长度就有22!,接近1.124×10^20,在当时的计算条件下(2004年)需要花费近14个小时。

作者给出了一个灵机一动的算法，其基本思路是给具有相同变位词的单词一个相同的标识，然后讲这些具有相同标识的单词聚集起来。这样就将问题转化为:

1. 如何产生标识，可以采用Hash算法，但文中采用的是更为简单的将单词中字母排序；
2. 如何将单词聚集起来: 只需要将单词按照其标识排序，然后对相邻的单词比较即可。

虽然思路和代码现在看起来都很简单，但是这样的算法经过了长久的考研，依然是现在常用的基本操作，可见这样的代码称得上是真正的珠玑。

Rust代码实现

#[derive(Debug)]
struct Word {
    sign:String,
    word:&'static str
}

fn init_words()->Vec<Word>{
  let w = Word{sign:String::from(""),word:"pans"};
  let mut v = vec![w];
  let w = Word{sign:String::from(""),word:"pots"};
  v.push(w);
  let w = Word{sign:String::from(""),word:"opt"};
  v.push(w);
  let w = Word{sign:String::from(""),word:"snap"};
  v.push(w);
  let w = Word{sign:String::from(""),word:"stop"};
  v.push(w);
  let w = Word{sign:String::from(""),word:"tops"};
  v.push(w);
  v
} 
  //通过对每个单词排序生成标识(sign)，便于后面排序组装
fn generate_sign(words:&mut Vec<Word> ){
  for w in words{
    let mut chars:Vec<char> = w.word.chars().collect();
    chars.sort_by(|a,b| a.cmp(b));
    w.sign = String::from_iter(chars);
  }
}

fn main() {
    let mut words = init_words();
    generate_sign(&mut words);
    //对所有的Words按照其标识sign排序
    words.sort_by(|a,b|a.sign.cmp(&b.sign));
    //所有标识相同的输出为一行
    let mut old_sign = &String::from("");
    for w in &words{
        if &w.sign != old_sign{
            old_sign = &w.sign;
            println!("")
        }
        print!("{} ",w.word);
    }
    println!()
}