DeFi借贷概念 #1 - 借与贷

理解借贷协议的份额币及借贷利息计算逻辑

这篇文章是借贷系列文章的一篇，在这篇文章里，我们回顾 DeFi 协议如何进行借贷。

我们见讨论DeFi借贷协议如何工作， 它们的关键组成部分、公式和使用案例。在这个过程中，我们将强调，尽管各协议有不同的命名，协议往往使用类似的的核心概念。我们在这篇博文中详细写到的一个这样的共享核心概念实现，就是使用ERC20代币来代表用户在借贷池中的份额。我们将首先强调这些协议的独特概念元素，并提供技术概念来区分它们的工作方式。

阅读完本文，将了解到以下概念：

  • 借贷池

  • 份额币（Share Token）

  • aToken：AAVE 的份额币

  • cToken：Compound 的份额币

  • eToken：Euler 的份额币。

借贷池（Lending Pools）

在传统金融（或TradFi）中，借贷是由第三方的金融机构来调解的。这些金融机构被赋予两个关键任务：强制借款方向贷款方支付利息，以及评估和防止被认为不值得信任的各方参与这些活动。

相比之下，在去中心化金融（或DeFi）中，第三方贷款人和借款人是不被信任的（没有担保）。这种缺乏信任的情况激发了一种促进链上借贷过程的新颖设计。

一个借贷池是一个智能合约。DeFi协议的用户可以存入资产（通常是ERC20代币），目的是使用这个合约来借出他们存入的资产。其他用户可以与借贷池交互，享受即时贷款--用存入池中的抵押资产进行借贷。

与传统的金融方法相比，借贷池有一些重大的好处，比如说：

  • 通过DeFi，贷款不受借出资金与借入金额1:1的可用性限制。相反，来自该协议所有用户的资金被存入资金池--从而创造出足够大的代币库存，以立即满足贷款需求。
  • DeFi摒弃了还款时间表。贷款是使用以前存入代币作为抵押品，用户可以选择在任何时候偿还。

在这一点上，你可能会想："如果我必须提供同等价值（甚至更高估值）的资产作为抵押，我为什么要在借贷协议上借入资产？我不是应该卖掉抵押品，然后买下借来的资产吗？"

不是的，看上去DeFi借贷协议似乎只允许完全（或超额）抵押的贷款，但这为一种有趣的 "交易 "方法打开了大门：杠杆交易。

想象一下，你看好WBTC--100%肯定它的价值会暴涨！你可以存入一些WBTC（比如说，你可以把WBTC存入银行）！你可以在你最喜欢的贷款协议上存入一些WBTC（比如价值1000美元），用它来借一些稳定币（即USDC），然后你可以在一些交易所购买更多的WBTC（在我们的场景中，让我们假设你初始存款的一半--500美元）。在此案例中，你将从最初的1000美元中获得1500美元的WBTC风险资金。

但是，等等，还有更多!如果你将价值500美元的WBTC抵押品存入，并以其为抵押借入更多的USDC呢？这个过程被称为过度杠杆化，你可以反复这样做，直到协议的政策停止这样做，一旦你超过了你的借贷能力。

在类似情况下，假设你看跌WBTC（毕竟现在是加密货币的冬天❄️）。你可以采取与之前的方案相反的做法，存入USDC作为抵押品来借入WBTC，并立即卖出 WBTC 以获得更多的稳定币。如果你的预测如实，WBTC的价格下跌，那么你可以在交易所以更低的价格买入相同数量的WBTC ，偿还你的债务，多余的USDC则是自己的利润

份额币（Share Tokens）

与TradFi一样，将资产存入借贷池的用户被激励将其资金长期保留在借贷池中，他们的存款会产生利息。利息随着时间的推移而累积，协议按用户在借贷池中的存款比例来计算，并由其各自的存款用户索取。用户在借贷池中保持其资产的时间越长，他们应计的利息就越多。

协议是如何核算每个用户在池子里的份额的？请记住，当一个用户将资产存入资金池时，他们的 "份额" 会稀释所有用户的份额，协议也会相应地反映这一点。然而，协议并不直接跟踪和更新每个用户在资金池中的份额，在每一次提款或存款的时候。在链上这样做会造成巨大的浪费，而且对储户来说成本过高，储户得为每次更新动作买单。

相反，该协议被设计为只处理储户份额的变化，而不需要主动更新其他用户的份额。

协议通过铸造和燃烧ERC20代币来处理利息的发行，我们将其称为 "份额币（Share Tokens）"，代表贷款人在其贷款池中的份额（或标的资产存款的比例）。"份额币 "的设计会自动调整其他 "股东（存款人）" 的股份稀释，以反映 "股份" 的铸造和燃烧，分别与他们的标的资产的存入或提取对应。

下面，我们将提供不同协议采用 "份额币" 的真实例子，并讨论其相似性。

aToken：AAVE 的份额币

aToken 是 AAVE 的可产生收益的代币，由借贷池在向协议存入和提取资产时分别铸造和燃烧。

aToken是AAVE协议中的类似ERC20的代币，这样，用户可以进入的每个市场都有一个aToken（将抵押品存入）。

每个 aToken 合约对应一个市场

如果我们看一下 AAVE 借贷池合约，可以看到当用户将资产存入池中时发生的底层操作：

pragma solidity ^0.8.13;

function deposit(
  address asset,
  uint256 amount,
  address onBehalfOf,
  uint16 referralCode
) external override whenNotPaused {
  DataTypes.ReserveData storage reserve = _reserves[asset];

  ValidationLogic.validateDeposit(reserve, amount);

  address aToken = reserve.aTokenAddress;

  reserve.updateState();
  reserve.updateInterestRates(asset, aToken, amount, 0);

  IERC20(asset).safeTransferFrom(msg.sender, aToken, amount);

  bool isFirstDeposit = IAToken(aToken).mint(onBehalfOf, amount, reserve.liquidityIndex);

  if (isFirstDeposit) {
    _usersConfig[onBehalfOf].setUsingAsCollateral(reserve.id, true);
    emit ReserveUsedAsCollateralEnabled(asset, onBehalfOf);
  }

  emit Deposit(asset, msg.sender, onBehalfOf, amount, referralCode);
}

源码

我们可以看到，与用户存入的市场相对应的aToken将被调用，并有mint函数。

pragma solidity ^0.8.13;

function mint(
  address user,
  uint256 amount,
  uint256 index
) external override onlyLendingPool returns (bool) {
  uint256 previousBalance = super.balanceOf(user);

  uint256 amountScaled = amount.rayDiv(index);
  require(amountScaled != 0, Errors.CT_INVALID_MINT_AMOUNT);
  _mint(user, amountScaled);

  emit Transfer(address(0), user, amount);
  emit Mint(user, amount, index);

  return previousBalance == 0;
}

源码

我们可以看到，实际要铸造的数量是：

img

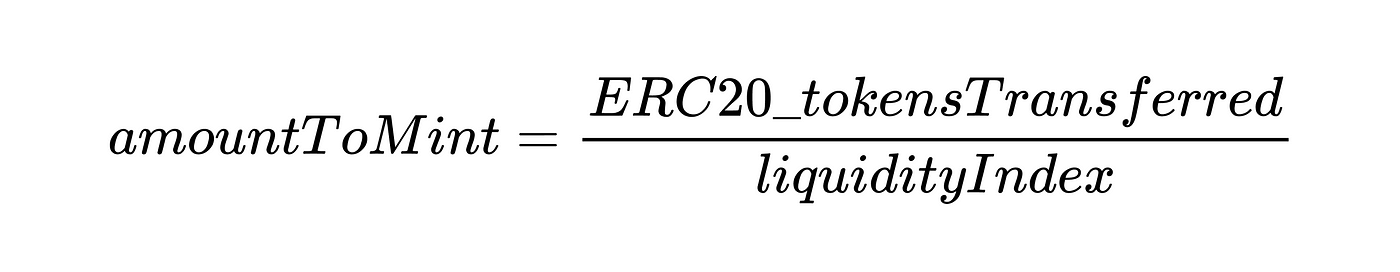
在我们的例子中，用户已经加入的市场，其储备已经在他们之前存入的资产上累积了一些利息。上面的等式有助于我们理解这一点，因为它显示了如何用一个在各种行动（存款、取款等）中更新的全局指数来说明所有用户的利息累积。

译者注：liquidityIndex 是一个累积量，理解这一点很关键

当用户提取他们的标的资产时，liquidityIndex 被用作一个乘数来计算交易中所持有的代币数量。

下面是借贷池合约取款的相关代码片段：

pragma solidity ^0.8.13;

function withdraw(
  address asset,
  uint256 amount,
  address to
) external override whenNotPaused returns (uint256) {
  DataTypes.ReserveData storage reserve = _reserves[asset];

  address aToken = reserve.aTokenAddress;

  uint256 userBalance = IAToken(aToken).balanceOf(msg.sender);

  uint256 amountToWithdraw = amount;

  if (amount == type(uint256).max) {
    amountToWithdraw = userBalance;
  }

  ValidationLogic.validateWithdraw(
    asset,
    amountToWithdraw,
    userBalance,
    _reserves,
    _usersConfig[msg.sender],
    _reservesList,
    _reservesCount,
    _addressesProvider.getPriceOracle()
  );

  reserve.updateState();

  reserve.updateInterestRates(asset, aToken, 0, amountToWithdraw);

  if (amountToWithdraw == userBalance) {
    _usersConfig[msg.sender].setUsingAsCollateral(reserve.id, false);
    emit ReserveUsedAsCollateralDisabled(asset, msg.sender);
  }

  IAToken(aToken).burn(msg.sender, to, amountToWithdraw, reserve.liquidityIndex);

  emit Withdraw(asset, msg.sender, to, amountToWithdraw);

  return amountToWithdraw;
}

源码

在这里，aToken合约的balanceOf功能是很奇怪的! 毕竟，我们刚刚确定，铸造的aTokens的数量与存入的标的资产的数量有偏差。为什么调用IAToken(aToken).balanceOf(address(user))会产生要提取的标的资产的数量（如函数底部所示）？ 是这样的：

  • 当用户提取他们的资产时，其对应的aTokens被销毁。这些 aTokens被销毁后，其他用户拥有的 aTokens总量与他们在用户资产被提取后在资金池中的份额依旧成正比。
  • 用户提取资金的市场的利率随着每次提取而更新。

img

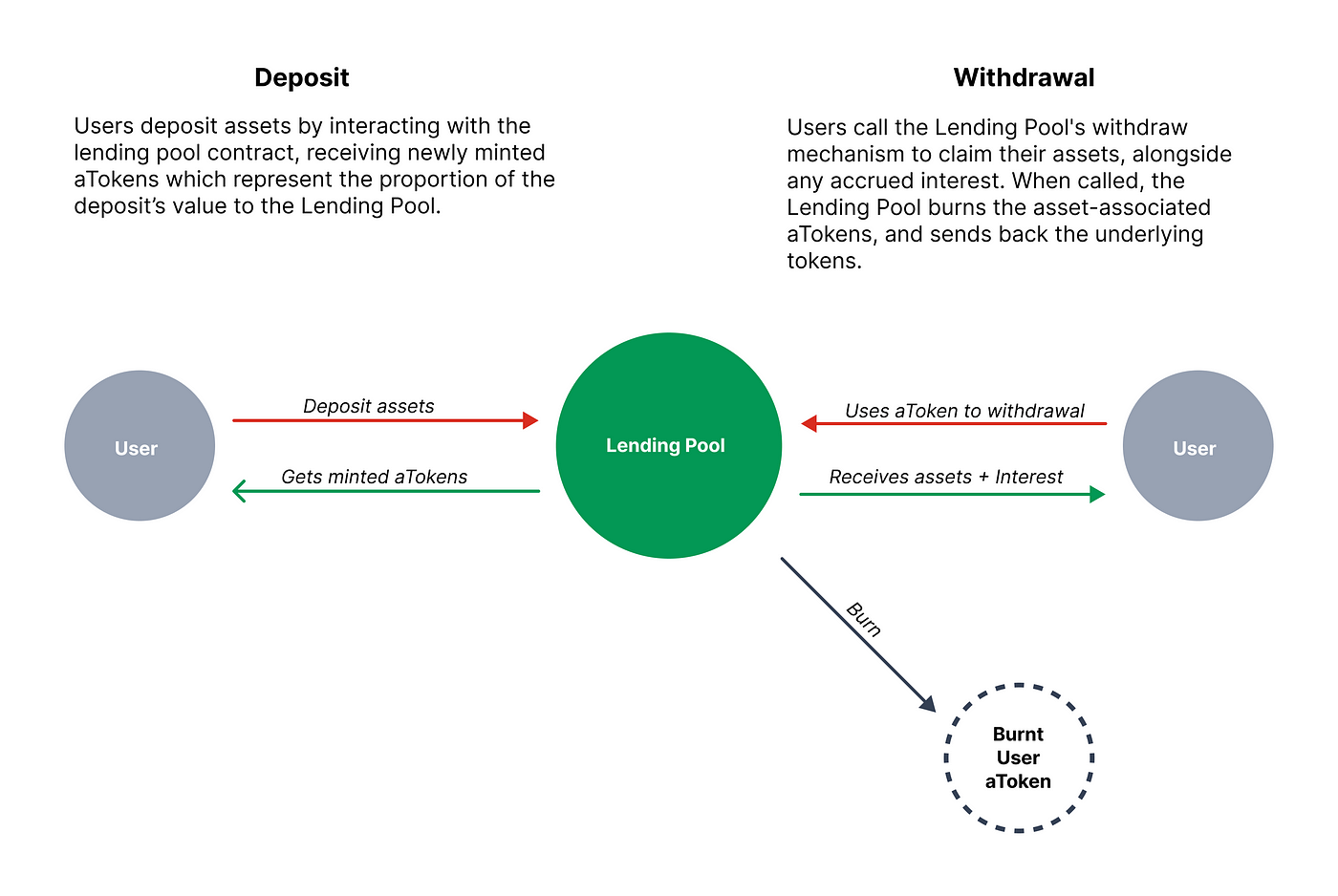
正如我们之前介绍的，aTokens是类似ERC20的代币。我们强调它们 像ERC-20代币，是因为它的 balanceOf函数有独特属性。在常规的ERC20代币中，balanceOf函数仅是返回一个地址拥有的代币数量。

因为aToken代表了资金池的份额，而不是直接的价值，aToken的balanceOf函数返回协议”欠“用户的标的(underlying)代币的数量，用于他们的存款。

pragma solidity ^0.8.13;

function balanceOf(address user)
  public
  view
  override(IncentivizedERC20, IERC20)
  returns (uint256)
{
  return super.balanceOf(user).rayMul(_pool.getReserveNormalizedIncome(_underlyingAsset));
}

源码

这里，这个balanceOf函数重写了被继承的aToken合约中的balanceOf。因此，这个例子的balanceOf逻辑被执行，而不是被继承的的token数量的映射查询。

上面提到的代币数量然后乘以 getReserveNormalizedIncome的结果，它执行了以下逻辑：

pragma solidity ^0.8.13;

function getNormalizedIncome(DataTypes.ReserveData storage reserve)
  internal
  view
  returns (uint256)
{
  uint40 timestamp = reserve.lastUpdateTimestamp;

  if (timestamp == uint40(block.timestamp)) {
    return reserve.liquidityIndex;
  }

  uint256 cumulated =
    MathUtils.calculateLinearInterest(reserve.currentLiquidityRate, timestamp).rayMul(
      reserve.liquidityIndex
    );

  return cumulated;
}

源码

我们可以分析这里的分支条件：

  • 如果在该块中已经发生了对储备金数据的更新：返回该市场的liquidityIndex值，因为它已经被更新。
  • 否则：我们需要看看在calculateLinearInterest中发生了什么，以找出要执行的下一个流程：
pragma solidity ^0.8.13;

function calculateLinearInterest(uint256 rate, uint40 lastUpdateTimestamp)
  internal
  view
  returns (uint256)
{
  uint256 timeDifference = block.timestamp.sub(uint256(lastUpdateTimestamp));

  return (rate.mul(timeDifference) / SECONDS_PER_YEAR).add(WadRayMath.ray());
}

源码

市场的ReserveData对象中的currentLiquidityRate和lastUpdateTimestamp被传入这个函数，结果将是：

img

让我们来分解这个等式的组成部分，以更好地理解linearInterest值的要点：

  • currentLiquidityRate：可以把它看作是我们所在市场的APY（Annual Percentage Yield ：年化收益率）。
  • block_{timestamp}- lastUpdatedTimestamp：自上次更新以来的时间。

注意：由于我们在getNormalizedIncome中的第2个语句，所以保证这个值在此时是正数!

因此，我们可以把这种应计利息的机制看作是一种简单的利息复利机制，每一个区块都是复利。

现在我们已经确定了用户的应计利息金额，我们只需要将这个值乘以 liquidityIndex（流动性指数），就可以得到用户的正常收入（NormalizedIncome），在balanceOf函数中相乘：

img

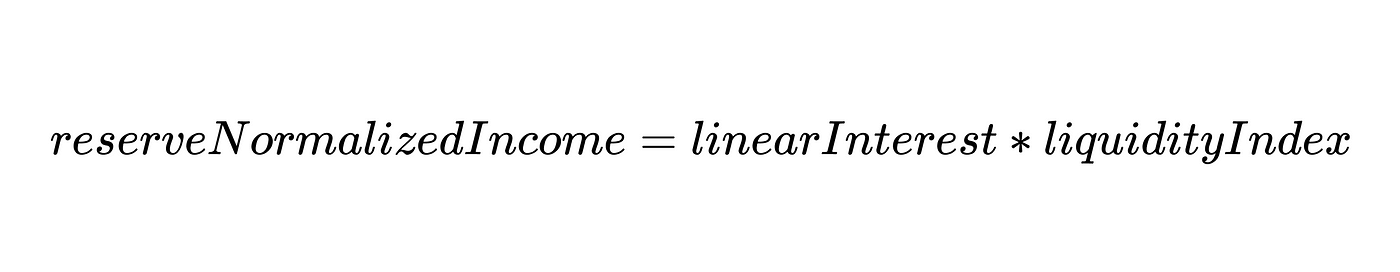
现在我们理解了aToken背后的逻辑，但我们仍然要解决liquidityIndex如何工作的。

在下面的例子中，流动性指数可以定义为储备金在一定时期内积累的利息：

pragma solidity ^0.8.13;

function _updateIndexes(
  DataTypes.ReserveData storage reserve,
  uint256 scaledVariableDebt,
  uint256 liquidityIndex,
  uint256 variableBorrowIndex,
  uint40 timestamp
) internal returns (uint256, uint256) {
  uint256 currentLiquidityRate = reserve.currentLiquidityRate;

  uint256 newLiquidityIndex = liquidityIndex;
  uint256 newVariableBorrowIndex = variableBorrowIndex;

  if (currentLiquidityRate > 0) {
    uint256 cumulatedLiquidityInterest =
      MathUtils.calculateLinearInterest(currentLiquidityRate, timestamp);
    newLiquidityIndex = cumulatedLiquidityInterest.rayMul(liquidityIndex);
    require(newLiquidityIndex <= type(uint128).max, Errors.RL_LIQUIDITY_INDEX_OVERFLOW);

    reserve.liquidityIndex = uint128(newLiquidityIndex);

    if (scaledVariableDebt != 0) {
      uint256 cumulatedVariableBorrowInterest =
        MathUtils.calculateCompoundedInterest(reserve.currentVariableBorrowRate, timestamp);
      newVariableBorrowIndex = cumulatedVariableBorrowInterest.rayMul(variableBorrowIndex);
      require(
        newVariableBorrowIndex <= type(uint128).max,
        Errors.RL_VARIABLE_BORROW_INDEX_OVERFLOW
      );
      reserve.variableBorrowIndex = uint128(newVariableBorrowIndex);
    }
  }

  reserve.lastUpdateTimestamp = uint40(block.timestamp);
  return (newLiquidityIndex, newVariableBorrowIndex);
}
}

源码

回顾之前的 liquidityRate变量 -- 现在我们将讨论它在 "liquidityIndex "的计算。只有当 "liquidityRate" 大于0时，才会有利息的积累，换句话说，只有在该市场有APY的情况下。这是有道理。

让我们快速回顾一下calculateLinearInterest的实际作用：

pragma solidity ^0.8.13;

function calculateLinearInterest(uint256 rate, uint40 lastUpdateTimestamp)
  internal
  view
  returns (uint256)
{
  uint256 timeDifference = block.timestamp.sub(uint256(lastUpdateTimestamp));

  return (rate.mul(timeDifference) / SECONDS_PER_YEAR).add(WadRayMath.ray());
}

源码

上述逻辑可转化为以下方程式：

img

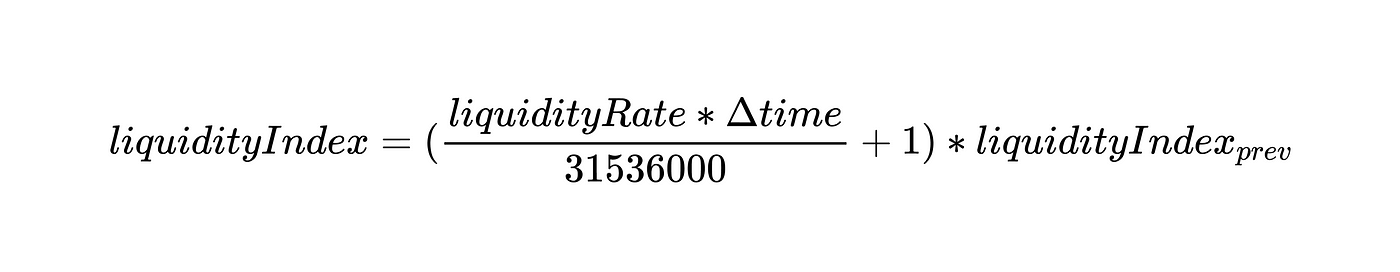
正如我们在DefaultReserveInterestRateStrategy.sol合约中看到的，liquidityRate 的定义是：


pragma solidity ^0.8.13;

function calculateInterestRates(
    address _reserve,
    uint256 _availableLiquidity,
    uint256 _totalBorrowsStable,
    uint256 _totalBorrowsVariable,
    uint256 _averageStableBorrowRate
)
    external
    view
    returns (
        uint256 currentLiquidityRate,
        uint256 currentStableBorrowRate,
        uint256 currentVariableBorrowRate
    )
{

uint256 utilizationRate = (totalBorrows == 0 && _availableLiquidity == 0)
      ? 0
      : totalBorrows.rayDiv(_availableLiquidity.add(totalBorrows));

// ...

currentLiquidityRate = getOverallBorrowRateInternal(
        _totalBorrowsStable,
        _totalBorrowsVariable,
        currentVariableBorrowRate,
        _averageStableBorrowRate
    )
        .rayMul(utilizationRate);

}

源码

因此，它可以写成：

img

这里又定义了 "总体借贷率"（overallBorrowRate）：

pragma solidity ^0.8.13;

function getOverallBorrowRateInternal(
    uint256 _totalBorrowsStable,
    uint256 _totalBorrowsVariable,
    uint256 _currentVariableBorrowRate,
    uint256 _currentAverageStableBorrowRate
) internal pure returns (uint256) {
    uint256 totalBorrows = _totalBorrowsStable.add(_totalBorrowsVariable);

    if (totalBorrows == 0) return 0;

    uint256 weightedVariableRate = _totalBorrowsVariable.wadToRay().rayMul(
        _currentVariableBorrowRate
    );

    uint256 weightedStableRate = _totalBorrowsStable.wadToRay().rayMul(
        _currentAverageStableBorrowRate
    );

    uint256 overallBorrowRate = weightedVariableRate.add(weightedStableRate).rayDiv(
        totalBorrows.wadToRay()
    );

    return overallBorrowRate;
}
}

源码

而我们可以把它写成：

img

img

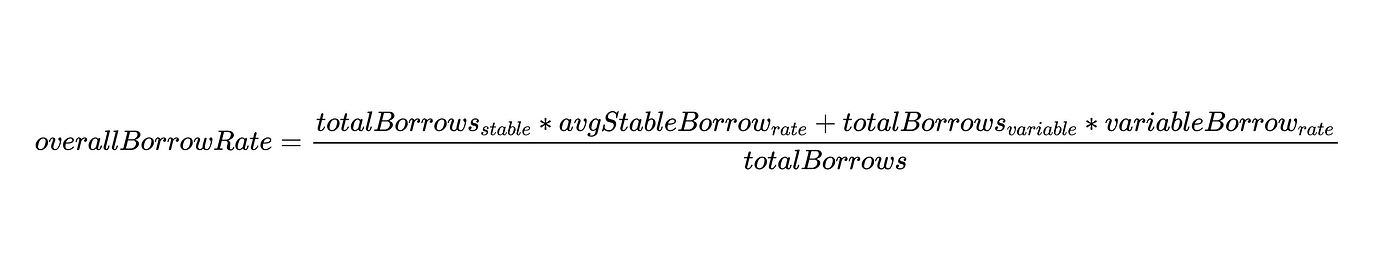
而 "利用率utilizationRate" 可以被定义为：

img

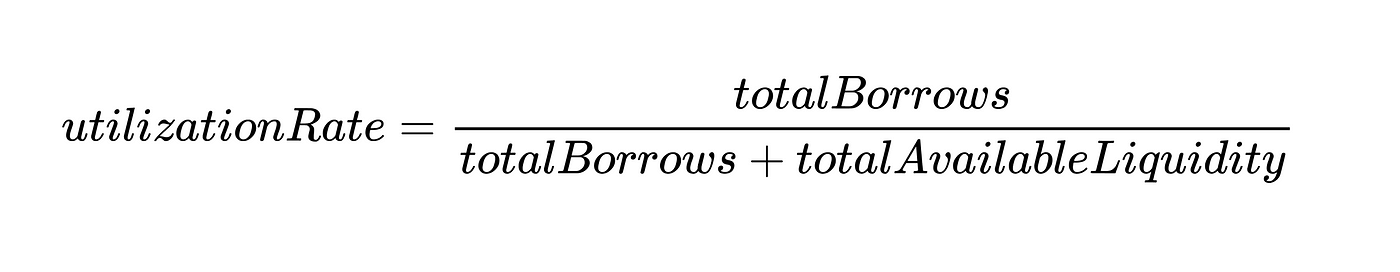
在定义利用率时，更容易想到它是储备中的流动性（目前借来的）与市场上总的流动性之间的比率，可以简化为：

img

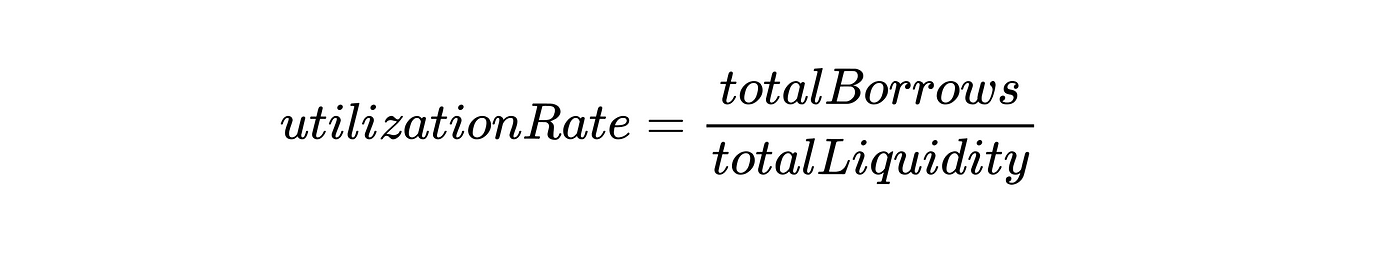
现在我们可以用这两个定义来写下流动性比率（liquidity rate）的方程式：

img

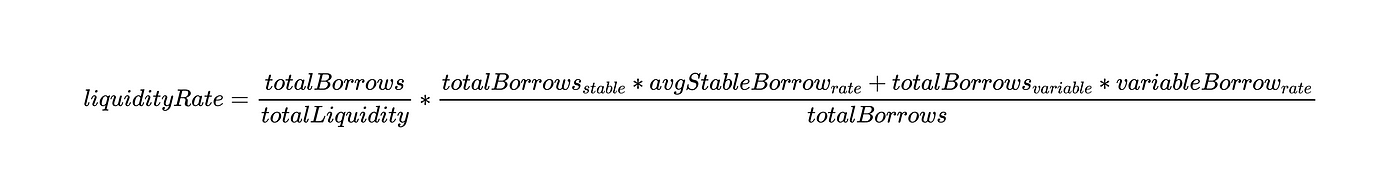
由于 totalBorrows 在分子和分母中都有，我们可以推出：

img

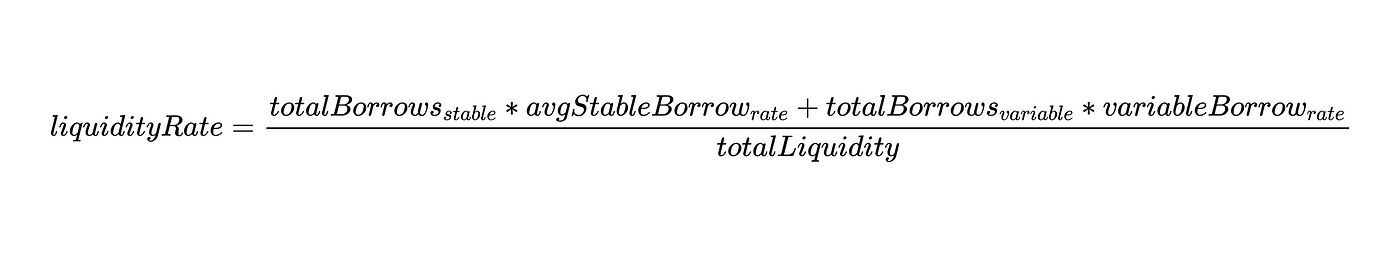
现在，我们对 "流动性比率"的公式的阐述就到此为止。我们以后会再来讨论这个定义。

cToken：Compound 的份额币

让我们继续看下一个借贷协议的例子：Compound。

Compound使用一个叫做 "cToken" 的份额币来处理借贷。这个代币为Compound协议中用户可用于借贷的所有资产进行记账。

与我们讨论的 AAVE V2 类似，Compound的 "份额币" 被铸造并用于赎回标的资产。

Compound使用一个兑换率（exchange rate），类似于AAVE V2的流动性指数，来决定应该铸造多少cToken。这个兑换率是一个函数：


pragma solidity ^0.8.13;

function exchangeRateStoredInternal() internal view returns (MathError, uint) {
    uint _totalSupply = totalSupply;
    if (_totalSupply == 0) {
        return (MathError.NO_ERROR, initialExchangeRateMantissa);
    } else {
        uint totalCash = getCashPrior();
        uint cashPlusBorrowsMinusReserves;
        Exp memory exchangeRate;
        MathError mathErr;

        (mathErr, cashPlusBorrowsMinusReserves) = addThenSubUInt(totalCash, totalBorrows, totalReserves);
        if (mathErr != MathError.NO_ERROR) {
            return (mathErr, 0);
        }

        (mathErr, exchangeRate) = getExp(cashPlusBorrowsMinusReserves, _totalSupply);
        if (mathErr != MathError.NO_ERROR) {
            return (mathErr, 0);
        }

        return (MathError.NO_ERROR, exchangeRate.mantissa);
    }
}

源码

让我们来解释一下这里的关键术语：

  • totalCash（在合约留下的数量）：cToken 账户所拥有的ERC20 标的代币（underlying token）的数量。
  • totalBorrows（借出的总量）：从市场借出给借款人的 ERC20 标的代币的数量。
  • totalReserves（总储备金）：储备的 ERC20 标的代币的数量，可通过治理提取或转账。
  • totalSupply：ERC20函数，返回 cToken的总发行量。

有了这个背景，我们可以写出Compound的兑换率方程：

img

当用户存入ERC20代币时， 兑换率决定了会有多少cToken被铸造出来作为回报：


pragma solidity ^0.8.13;

function mintFresh(address minter, uint mintAmount) internal returns (uint, uint) {
    uint allowed = comptroller.mintAllowed(address(this), minter, mintAmount);
    if (allowed != 0) {
        return (failOpaque(Error.COMPTROLLER_REJECTION, FailureInfo.MINT_COMPTROLLER_REJECTION, allowed), 0);
    }

    if (accrualBlockNumber != getBlockNumber()) {
        return (fail(Error.MARKET_NOT_FRESH, FailureInfo.MINT_FRESHNESS_CHECK), 0);
    }

    MintLocalVars memory vars;

    (vars.mathErr, vars.exchangeRateMantissa) = exchangeRateStoredInternal();
    if (vars.mathErr != MathError.NO_ERROR) {
        return (failOpaque(Error.MATH_ERROR, FailureInfo.MINT_EXCHANGE_RATE_READ_FAILED, uint(vars.mathErr)), 0);
    }

    vars.actualMintAmount = doTransferIn(minter, mintAmount);

    (vars.mathErr, vars.mintTokens) = divScalarByExpTruncate(vars.actualMintAmount, Exp({mantissa: vars.exchangeRateMantissa}));
    require(vars.mathErr == MathError.NO_ERROR, "MINT_EXCHANGE_CALCULATION_FAILED");

    (vars.mathErr, vars.totalSupplyNew) = addUInt(totalSupply, vars.mintTokens);
    require(vars.mathErr == MathError.NO_ERROR, "MINT_NEW_TOTAL_SUPPLY_CALCULATION_FAILED");

    (vars.mathErr, vars.accountTokensNew) = addUInt(accountTokens[minter], vars.mintTokens);
    require(vars.mathErr == MathError.NO_ERROR, "MINT_NEW_ACCOUNT_BALANCE_CALCULATION_FAILED");

    totalSupply = vars.totalSupplyNew;
    accountTokens[minter] = vars.accountTokensNew;

    emit Mint(minter, vars.actualMintAmount, vars.mintTokens);
    emit Transfer(address(this), minter, vars.mintTokens);

    return (uint(Error.NO_ERROR), vars.actualMintAmount);
}

源码

而要铸造的cToken的数量由以下公式定义：

img

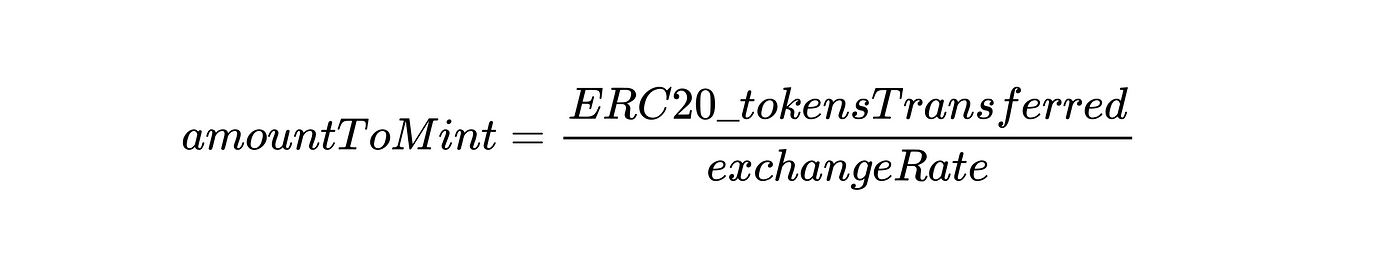
关于借贷协议利息的计算，还可参考： https://learnblockchain.cn/article/5036

eToken：Euler的份额币

为了进一步巩固这些协议的相似性，我们将分解另一个借贷协议： Euler，并看看它如何处理借贷。

在下面的例子中，存款函数让用户存入ERC20代币以换取......eToken。


pragma solidity ^0.8.13;

function deposit(uint subAccountId, uint amount) external nonReentrant {
    (address underlying, AssetStorage storage assetStorage, address proxyAddr, address msgSender) = CALLER();
    address account = getSubAccount(msgSender, subAccountId);

    updateAverageLiquidity(account);
    emit RequestDeposit(account, amount);

    AssetCache memory assetCache = loadAssetCache(underlying, assetStorage);

    if (amount == type(uint).max) {
        amount = callBalanceOf(assetCache, msgSender);
    }

    amount = decodeExternalAmount(assetCache, amount);

    uint amountTransferred = pullTokens(assetCache, msgSender, amount);
    uint amountInternal;

    unchecked {
        assetCache.poolSize -= amountTransferred;
        amountInternal = underlyingAmountToBalance(assetCache, amountTransferred);
        assetCache.poolSize += amountTransferred;
    }

    increaseBalance(assetStorage, assetCache, proxyAddr, account, amountInternal);

    if (assetStorage.users[account].owed != 0) checkLiquidity(account);

    logAssetStatus(assetCache);
}

源码

我们可以看到，internalAmount是为这次转账铸造的 eToken 的数量。

pragma solidity ^0.8.13;

function computeExchangeRate(AssetCache memory assetCache) private pure returns (uint) {
    uint totalAssets = assetCache.poolSize + (assetCache.totalBorrows / INTERNAL_DEBT_PRECISION);
    if (totalAssets == 0 || assetCache.totalBalances == 0) return 1e18;
    return totalAssets * 1e18 / assetCache.totalBalances;
}

function underlyingAmountToBalance(AssetCache memory assetCache, uint amount) internal pure returns (uint) {
    uint exchangeRate = computeExchangeRate(assetCache);
    return amount * 1e18 / exchangeRate;
}

源码

然而，与Compound的另一个直接重合：exchangeRate的名称和功能。

img

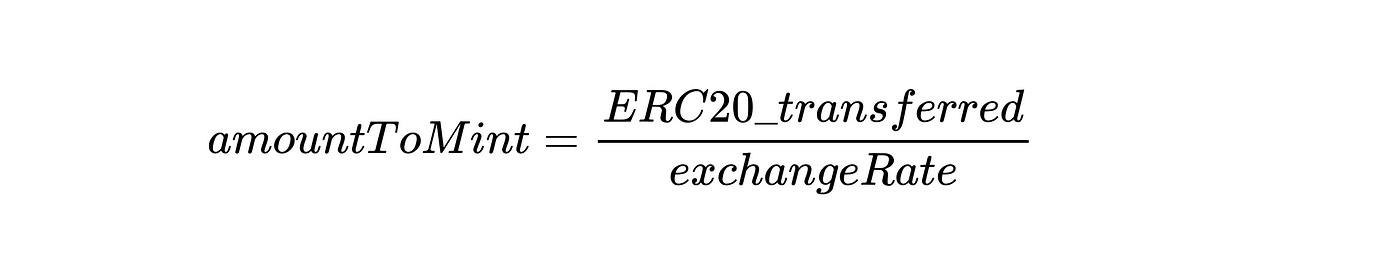
让我们解释一下用于计算兑换率的关键参数：

  • poolSize：标的资产ERC20合约对应池子地址上的余额，即调用balanceOf(池子地址)的结果。
  • totalBorrows：借入的ERC20总量，目前不在资金池中。
  • totalBalances：所有 eToken持有人的总余额。

因此，方程式将是：

img

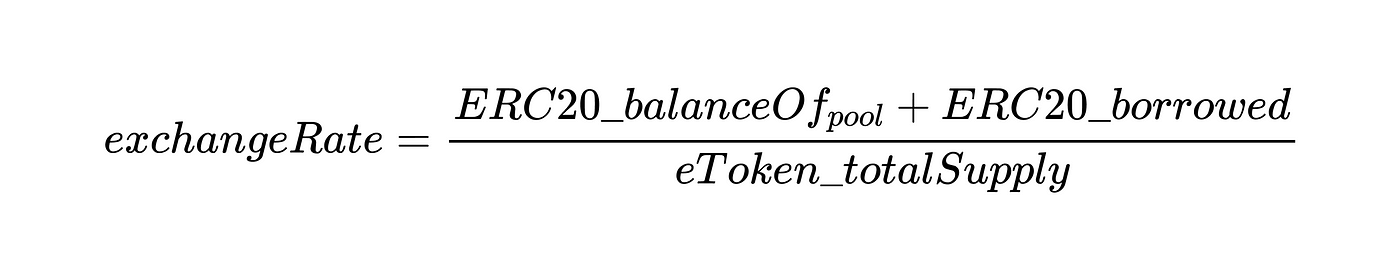
小结

回顾一下，我们已经涵盖了3个借贷协议：

  • AAVE V2
  • Compound
  • Euler

我们已经研究了 "份额币" 的铸造，以及它们如何通过借贷池兑换成存款资产。

我们提出的三个方程显示了这些过程是如何工作的，可以归纳为这个简单的方程：

img

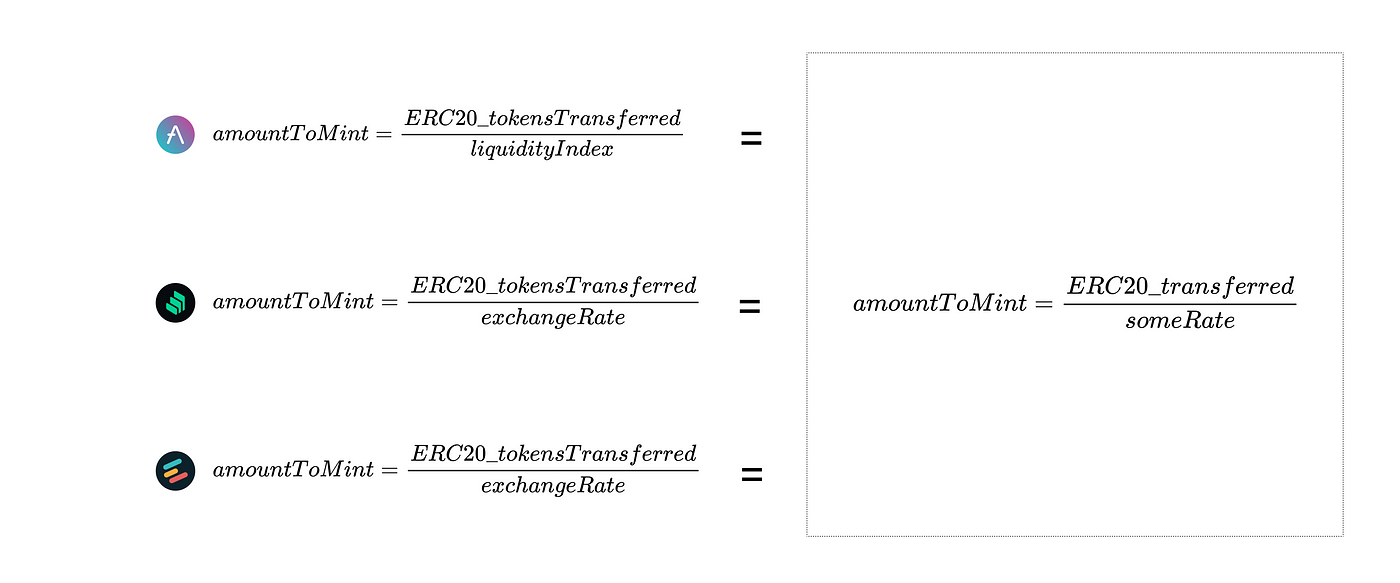
请记住，兑换率（exchange rate）可以用协议规定的任何方式来定义。在AAVE V2和Compound中，我们已经看到$someRate$变量的定义方式有一些相似之处。在Compound中，someRate是：

img

而在AAVE V2中，someRate 被定义为：

img

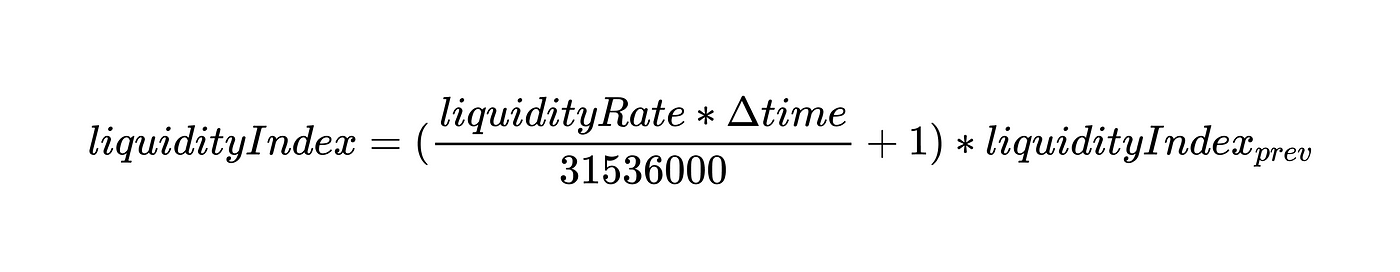
而 liquidity rate 定义为：

img

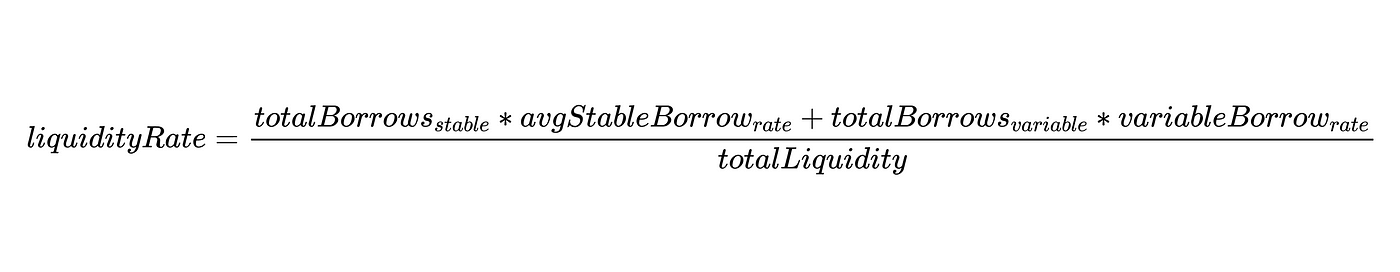
虽然我们不能概括每个协议的比率，但对于AAVE2和Compound，我们知道比率是市场上总流动性的函数。回到我们的方程上，鉴于 "总流动性(totalLiquidity)" 是市场上 ERC20 标的代币的总量，"兑换率(exchangeRate) "表达式中的分子和 liquidityRate 中的分母在功能上是一样的。

简单地说：这些协议实际上是相同的。虽然它们有时可能使用不同的术语，但当分解成方程式时，每个组件在执行中都有类似的目的。

作者：Tal 研究员 @ smlXL, 感谢 Sam Ragsdale 和为本帖提供建议和反馈的smlXL团队成员。

感谢 Chaintool 对本翻译的支持， Chaintool 是一个为区块链开发者准备的开源工具箱

点赞 6
收藏 10
分享
本文参与登链社区写作激励计划 ，好文好收益，欢迎正在阅读的你也加入。
该文章收录于 DEFI 协议解析
524 订阅 20 篇文章

0 条评论

请先 登录 后评论
翻译小组
翻译小组
0x9e64...7c84
大家看到好的文章可以在 GitHub 提 Issue： https://github.com/lbc-team/Pioneer/issues 欢迎关注我的 Twitter： https://twitter.com/UpchainDAO

翻译小组

如果觉得我的文章对您有用，请随意打赏。你的支持将鼓励我继续创作！