CycleFold Based Nova
- 白菜
- 发布于 2023-08-27 00:40
- 阅读 5290
背景下面这张图是revisitingnova中非常经典的描述cyclecurves的图:通过上面这张图,我们可以有以下共识:我们通常称上面一层电路为primary电路,下面一层电路为secondary电路。以secondary电路为例,secondary电路需要把prima
Thanks
- 非常感谢secbit labs的@郭宇老师 和 @even ,讨论过程中收获颇多,对folding 有了更抽象层次的理解
CycleFold 是什么
CycleFold 是针对NOVA系的folding scheme 在代码实现层面的优化技巧,适用于所有基于cycle curves 的诸如SuperNova/HyperNova/Protostar,使得电路的成本更低,原始paper 是针对HyperNova 进行地论证,为了陈述方便,本文是基于Nova的讨论。
<br /> 文章最后有一个自己的“思考”,是论文中没有涉及到的,感兴趣的欢迎讨论。
背景
下面这张图是revisiting nova 中非常经典的描述cycle curves 的图:
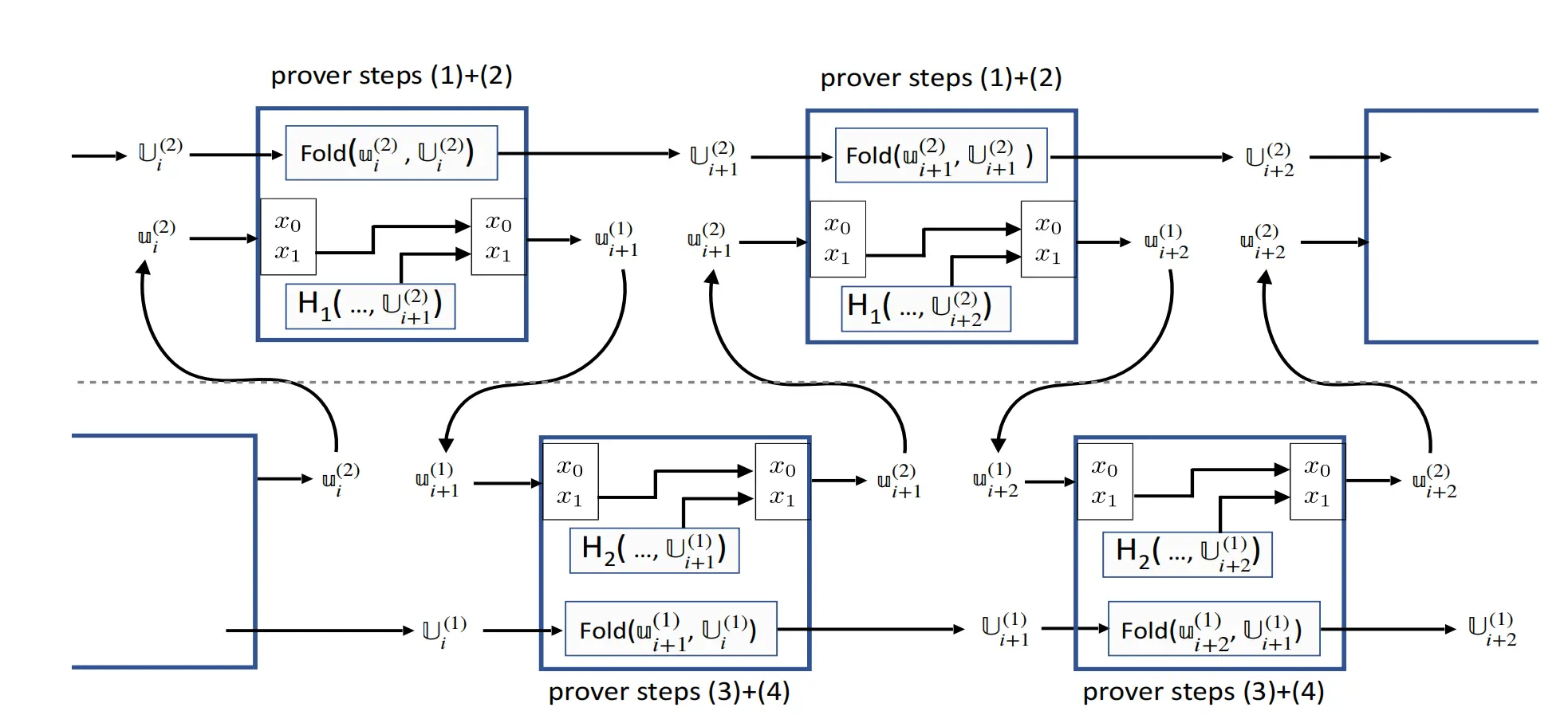
通过上面这张图,我们可以有以下共识:
- 我们通常称上面一层电路为primary 电路,下面一层电路为secondary 电路。以secondary 电路为例,secondary 电路需要把primary 电路的proof $u_i^{(1)}$ fold 进$Ui^{(1)}$,生成$U{i+1}^{(1)}$
<br />
- primary 电路会以public IO 形式吐出来两个hash值,$x_0$ 和 $x_1$,这两个hash会随着$u_i^{(1)}$ 传递给secondary 电路
<br />
先看一下$u_i^{(1)}$ 的数据结构:
pub struct AllocatedR1CSInstance<G: Group> {
pub(crate) W: AllocatedPoint<G>,
pub(crate) X0: AllocatedNum<G::Base>,
pub(crate) X1: AllocatedNum<G::Base>,
}<br />
再看一下$U_i^{(1)}$ 的数据结构:
pub struct AllocatedRelaxedR1CSInstance<G: Group> {
pub(crate) W: AllocatedPoint<G>,
pub(crate) E: AllocatedPoint<G>,
pub(crate) u: AllocatedNum<G::Base>,
pub(crate) X0: BigNat<G::Base>,
pub(crate) X1: BigNat<G::Base>,
}<br />
我们把folding的过程大概展开一下看看:
$$ \begin{aligned}
&U_{i + 1}^{(1)}.W \leftarrow U_i^{(1)}.W \overset{\text{fold}} \oplus r * u_i^{(1)}.W, \in \mathbb{F_q} \
&U_{i + 1}^{(1)}.E \leftarrow U_i^{(1)}.E \overset{\text{fold}} \oplus r * \widetilde{T}, \in \mathbb{F_q} \
&U_{i + 1}^{(1)}.u \leftarrow U_i^{(1)}.u \overset{\text{fold}} \oplus r * 1, \in \mathbb{F_q} \
&U_{i + 1}^{(1)}.x_0 \leftarrow U_i^{(1)}.x_0 \overset{\text{fold}} \oplus r * u_i^{(1)}.x_0, \textcolor{red} {\in \mathbb{F_p}} \
&U_{i + 1}^{(1)}.x_1 \leftarrow U_i^{(1)}.x_1 \overset{\text{fold}} \oplus r * u_i^{(1)}.x_1, \textcolor{red} {\in \mathbb{F_p}} \
\end{aligned} $$
<br />
folding的计算主要分为两种,一种是椭圆曲线上的点的folding,另一种是hash值的folding。 熟悉EC运算的应该知道第一种比较复杂的计算过程;而第二种就非常简单了。但因为它们分别属于两个不同的field,所以即使引入cycle curves也避免不了non-native计算,只是看孰轻孰重了。
<br />
椭圆曲线上的点的folding比较贵,所以,cycle curves 就尽量照顾到它,把它变成native 的计算,那么$x_0$ 和$x_1$ 的folding就变成了non-native的计算,最大限度的降低了电路的成本。细心地会发现,它是通过把field 转成bigint 来完成non-native 计算的。bigint 的计算成本也不算很低,但相对non-native的椭圆曲线点的计算肯定要低很多很多了。那么有没有更轻量级的secondary电路呢?
<br />
更轻量级的secondary 电路
有没有一种可能在secondary 电路中完全避开这种non-native的计算?产生non-native的根源在于我们把椭圆曲线点的folding 和 hash值的folding放在一个电路里做了,导致cycle curve只能二选一。那么有没有可能拆开,使得他们都在native field上?
<br />
下面这张图节选自Cycle-Fold 原文中比较经典的图:
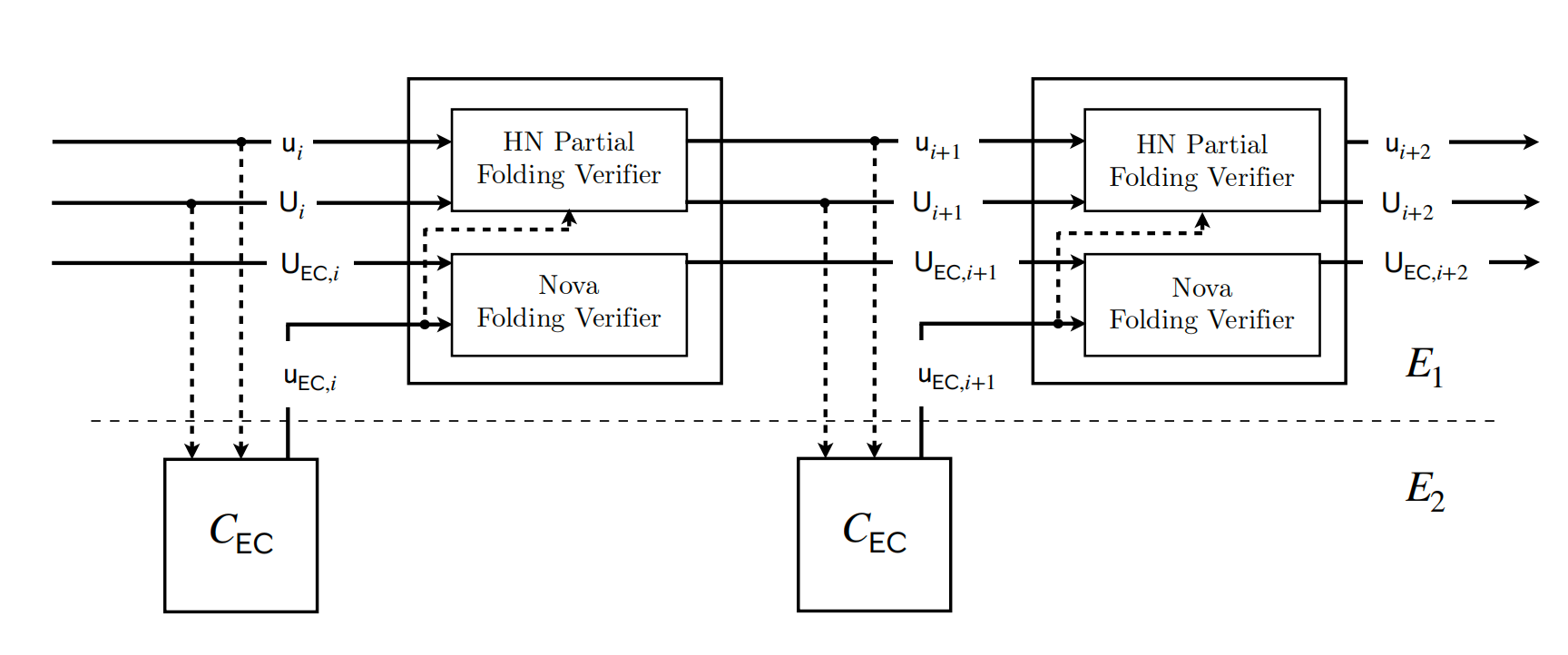
<br />
我们先描述一下它的宗旨:
- 把基于椭圆曲线E1 的primary 电路的proof $ui^{(1)}$ 中椭圆曲线的folding工作代理给基于椭圆曲线E2 的secondary 电路 $C{EC}$
<br />
- 剩余的两个hash 值$x_0$ 和 $x_1$ 的folding工作透传给下一个step 的primary 电路(HN Partial 部分),也就是说下一个step 的primary 电路会验证上一个step primary 电路
<br />
- secondary 电路 $C{EC}$的proof $u{EC}$ 还是交给primary 电路(Nova 部分)来完成(这里有个细节后面会提到)
<br />
下面主要把代理的整个过程给展开一下看看,对应上面的第1、2步:
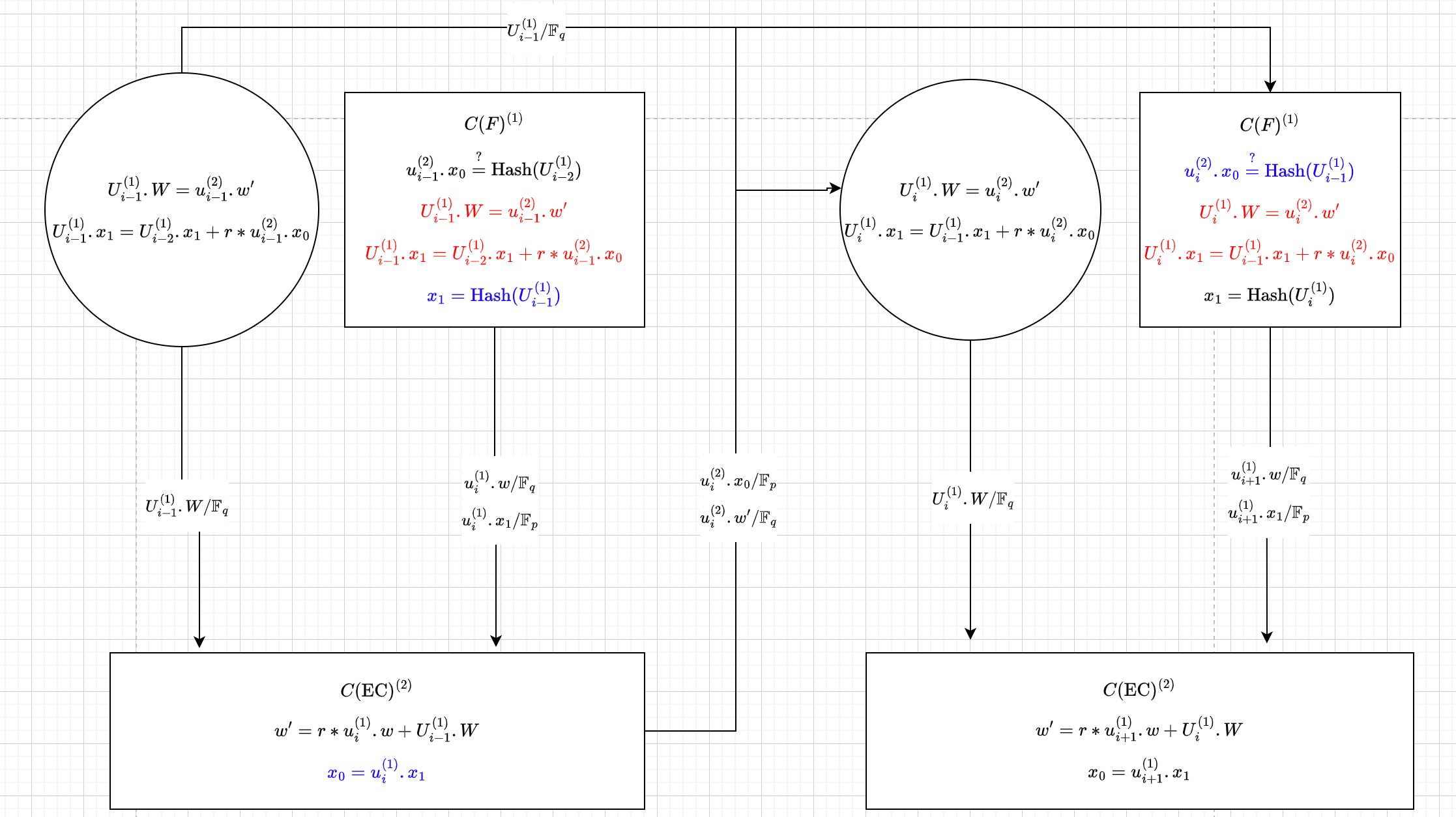
<br />
大概流程如下:
-
primary 电路吐出proof $ui^{(1)}$的时候,需要对当前电路更新后的状态$U{i−1}^{(1)}$ 进行hash,并publisize 给$u_i^{(1)}.x_1$,最后再通过$u_i^{(2)}$ 透传给下一个step 的primary 电路。
<br />
目的是,在下一个step 的primary 电路folding之前对电路 $C(EC)^{(2)}$ 的input $U_{i−1}^{(1)}$ 进行合法性校验,校验通过,就默认 电路 $C(EC)^{(2)}$ 对椭圆曲线点$u_i^{(1)}.w$ 的folding 结果$u_i^{(2)}.w′$是正确的,这样primary 电路就可以进行其它的工作了。
<br />
而电路$C(EC)^{(2)}$ 的验证工作是通过上面第3步中提到的primary 电路中的Nova folding verifier 来完成的,跟原始Nova的primary 电路一样,上图只是代理的过程,这部分就没有标出。
-
正是由于primary 电路吐出proof $u_i^{(1)}$中包含hash值 $u_i^{(1)}.x_1$,而电路 $C(EC)^{(2)}$ 只是完成了$u_i^{(1)}$中的$u_i^{(1)}.w$ 的folding,$u_i^{(1)}.x_1$ 的field 又刚好与primary 电路的field 相同,所以$u_i^{(1)}.x_1$ 的folding工作轮到了下一个step 的primary 电路。
<br />
到这里,Cycle-Fold 的核心理念就完成了。
<br />
思考
CycleFold 强调的是轻量级的secondary 电路,主要思想是最大限度地减轻secondary 电路的成本,只是负责代理 primary 电路的proof中的椭圆曲线点的计算,最后把代理计算的结果publisize后返回给primary 电路,primary 电路完成验证后接着就可以进行其它的工作了。
<br />
而secondary 电路本身的验证工作,同Nova一样,仍然需要primary 电路来做,secondary 电路吐出来的proof 中因为有public IO,所以secondary 电路proof 的folding 过程仍然免不了有少量的non-native 计算(1-2个)。
<br />
如果套用上面的思路,可不可以也把这部分non-native 的计算放到下一个step 的secondary 电路中呢?这样最终就会形成:primary 电路proof中椭圆曲线的计算代理给了secondary 电路,secondary 电路proof中的椭圆曲线的计算代理给了primary 电路,整个folding scheme中就完全避开了non-native 的计算。理论上是可行的,只是CycleFold原始论文中并没有提到这一点,它只是强调了轻量级的secondary 电路。
<br /> 最终的逻辑大概是这样子的:
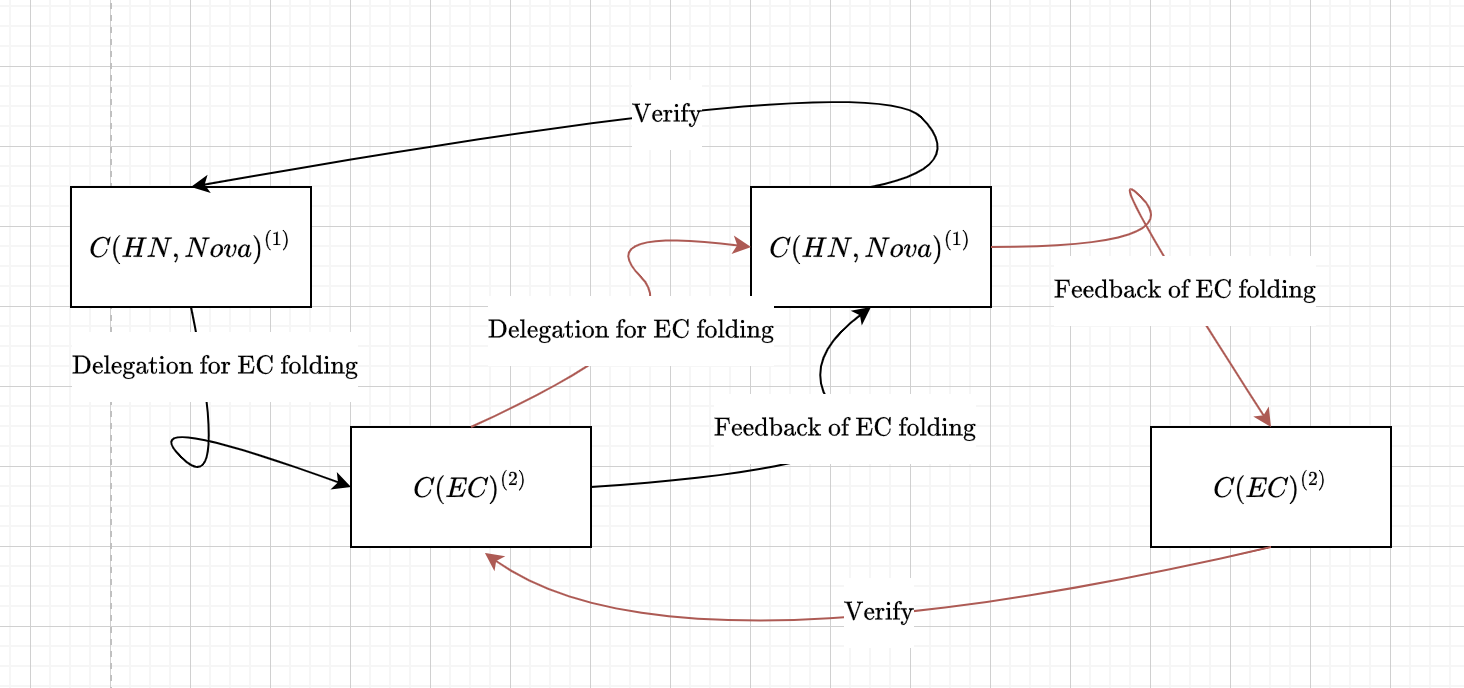
参考资料
【1】CycleFold论文: https://eprint.iacr.org/2023/1192.pdf
其它相关资料
【1】关于cycle curve更多的细节:https://learnblockchain.cn/article/6429
- 零知识API使用信用:大型语言模型及其他应用 23 浏览
- 民主事物的再思考:构建共识发现工具 149 浏览
- Zero 链: 技术定位报告 222 浏览
- 以太坊亟需的两大深度改造——二进制树 + VM 改造 258 浏览
- 以太坊 2029 Strawmap 傻瓜指南 303 浏览
- 不实的断言:攻破 6 个 zkVMs 209 浏览
- zERC20 在 Arbitrum 上线:最完备 L2 的原生隐私 392 浏览
- 零知识编年史:群 277 浏览
- 以太坊执行层优化:状态树与虚拟机 479 浏览
- 首批 ZK 漏洞利用事件已发生,但它们并非我们所预期 320 浏览
- 首次 ZK 攻击发生,且出乎意料 323 浏览
- Vitalik: 以太坊量子抵抗路线图 295 浏览

