本文翻译自 https://medium.com/@med456789d/uniswap-v3-math-insights-part-1-of-6-f85e1597b411，原系列标题为 Uniswap v3 Math Insights，共有六部分，此为第一部分。

为了让更多人可以访问和了解关于 Uniswap V3 投资的有用信息，我们翻译了系列文章，让中文读者对 Uniswap V3 机制和投资策略选择有更深入的理解。在阅读本翻译同时，可以随时参考原文以获取更多详细信息。

Uniswap v3的进步催生了一种通用的自动做市商（AMM），能够复制各种引人注目的收益结构。在这里，我们将介绍一个独特收益的示例，该示例利用了集中流动性。

简而言之:

• 类似Uniswap Analytics和Yewbow这样的工具可以帮助发现产生 LP 费用的交易量。

• 使用循环图这一统计工具（附录中提供的代码），可以识别价格范围的模式，从而帮助找到最小化发散损失（无偿损失）的交易点。

• +/- 84% 的价格边界范围优化了对称的最大范围，来减少在 LP 头寸中使用的资本（提高资本效率）的同时，避免市场价格走出可接受的范围。

v3 的快速视觉审查:

让我们通过 Lambert 的desmos文件进行一个小模拟，来可视化 Uniswap v3 上的 LP 头寸行为：

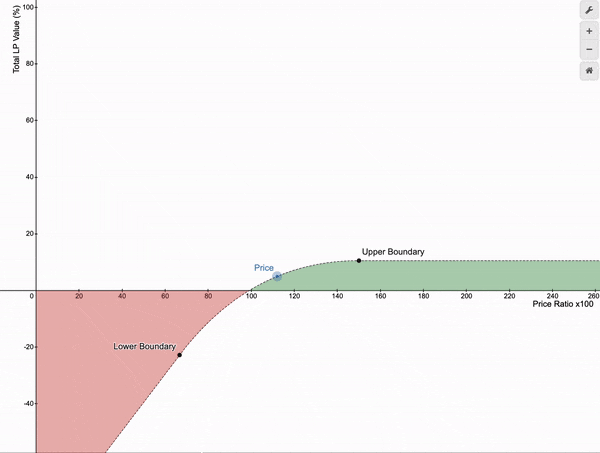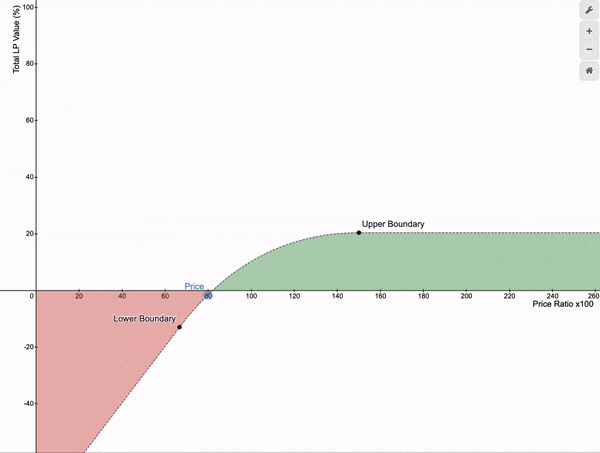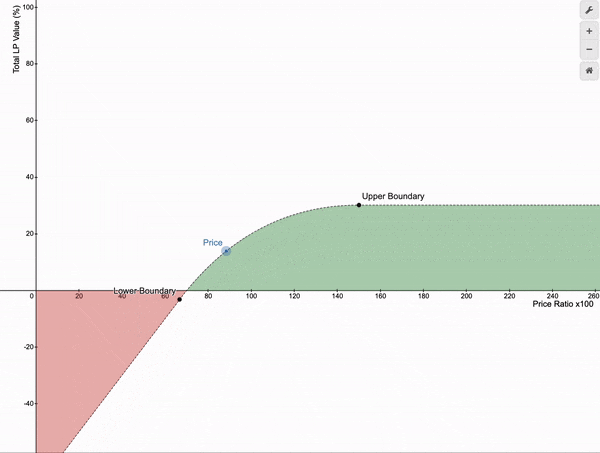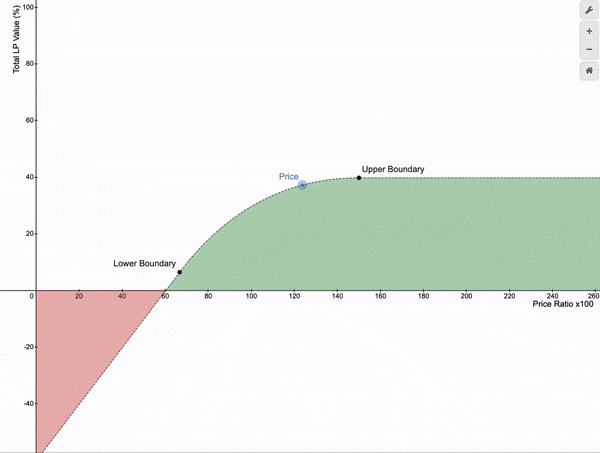如果价格在这些边界之间波动，LP 头寸的总价值会随着不同的费用而增长。

传统的 Uniswap v3 收益结构呈现出凸形（山丘状）的形态。以与进入时相同的比例退出、并使市场价格比率保持在做市价格范围的上下限之间是有收益的。但如果你在 LP 头寸中停留的时间较长会发生什么呢？假设你进入了一个 X/ETH 的 LP 头寸，其中 X 是与 ETH 相关的代币。有时它的表现会优于 ETH，而有时它的表现会不如预期，这取决于其他人在市场上买卖 X 的情况。

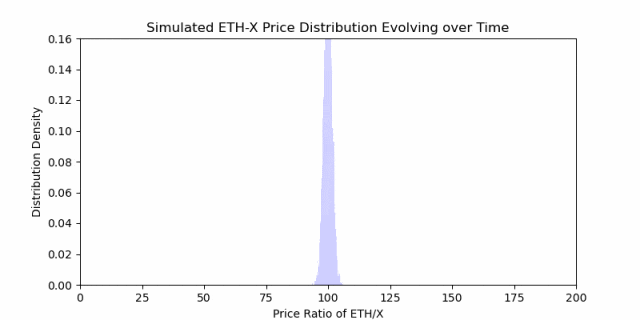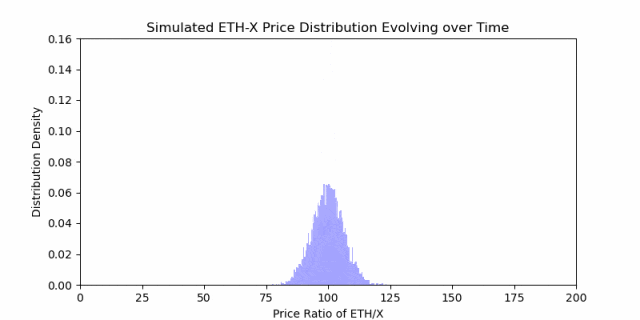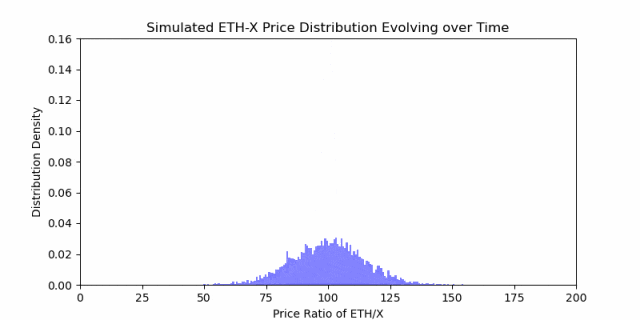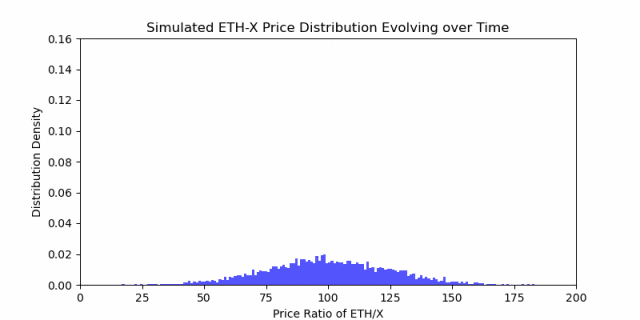等待的时间越长，越有可能与当前进场价格产生偏差。

正如上面分布动画中的膨胀所观察到的，随着时间的推移，X/ETH 的概率空间越来越扩大（波动性随时间的平方根演化）。这使得如果在随机的时间点退出，而此时 X/ETH 的比率与您最初进入时的比率不匹配，您更有可能发生发散损失（发散损失简单推理见附录）。然而，与此同时，作为 LP，您会从这个发散的山丘中获得费用收益。 这是 LP 所面临的主要权衡。

如何保持在山丘上以避免发散损失？从数学的角度来看，人们的目标是选择一个 X/Y 池， 该池具有较高的费用、高交易活动 以及 重新回到原始价格的高可能性 ，以便能够平仓 LP 头寸。

此外，还需要对 X 代币的协议风险（尽管 Euler 最近经历了六次专业审核仍然遭受黑客攻击）、团队/尽职调查风险（值得研究诈骗/欺诈/地毯模式）进行仔细研究，因为如果 X 发生风险事件并且X的价格暴跌，因为价格发散，LP 头寸将主要分配给 X。

在 Uniswap 上进行流动性提供（LPing）的核心要点如下：

1). 确定 交易量 发生的地点。
2). 找出价格回归到原始比率的地点，以最小化发散损失。我将这个比率称为 循环点 。
3). 选择一个最佳范围，以最小化资本使用并最大化范围。作为基本策略，我们将通过一些微积分找到，不论随机过程的性质如何，当我们对价格走势不确定时，+/- 84% 是我们的上下界限的限制。
让我们深入讨论每个要点：

1 — 交易量分析

在 Uniswap 上，LP 仅在发生交易时获得费用。更多的交易往往发生在具有交易量和价格波动性的资产周围。

• 确定一个代币是否有交易量可以通过 Uniswap Analytics 工具 https://info.uniswap.org/#/pools 来完成，按“volume”列进行排序。

• 另一种有趣的方法是通过 Yewbow 工具 https://info.yewbow.org/#/pools 按“ 隐含波动率 ”进行排序。隐含波动率（IV）关注费用和交易量与当前价格下锁定的总交易量之间的关系。 需要注意的是，这并不意味着这些交易对的风险/收益比是合理的。重要的是要注意，仅仅依靠隐含波动率可能是危险的，因为承诺过高的费用回报的资产很可能过于美好，事实并非如此。 因此，非常过高的IV应该受到谨慎怀疑，并对代币对进行尽职调查。

然而，找到具有高费用和交易量的池子还不够。人们必须要考虑到令人恐惧的 发散损失 。

2 — 循环点

作为 LP，人们希望 最大程度地增加回归/价格回归的机会 ，以最小化发散损失。这意味着人们从 X/ETH 的某个比率开始，比如 2/1，并希望在未来的某个时间重新回到 2/1。在统计学中，用于发现回归的一个有用工具是查看循环图。这些图允许我们看到系统何时再次回到特定点，比如比率，随着时间的推移。让我们来看一些示例，然后是一个 LP 的示例，以及这些循环图如何帮助我们。

2.1 — 简单的循环模型 让我们看一个涉及 随着时间减弱的摆动钟摆 的简单系统的循环图（蓝线）。可以将这个简单模型看作是市场崩盘后的归一化，或者是新协议代币（如 Arbitrum 空投）发布后的平衡价格的发现，或者是协议被黑客攻击并对价格产生影响。在这里，我们的系统是可预测的、非混沌的，但随着时间的增加，系统变得更加可预测，并且系统稳定在一个位置上，因此也就无法产生更多的LP费用。没有价格波动 — 没有 LP 费用。

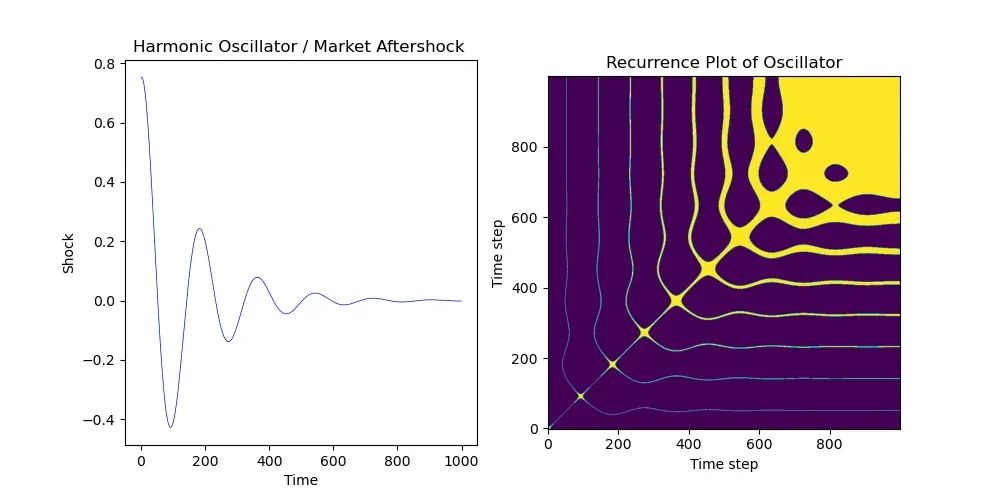最近Arbitrum代币的推出展现了类似的振荡然后减弱的模式。

右侧的循环图捕捉到了这一模式，颜色越黄，点在时间中重新访问的可能性越大。随着系统在特定范围内稳定，注意当发散减少时，它会在右上方变得更加明亮。

2.2 — 混沌的循环模型
然而，上述模型的简单性并不能准确描述价格动态的现实情况。首先，我们必须注意，当人们买卖一个代币时，所购买的数量会以 非线性 的方式影响价格。此外，我们还必须注意，由于区块链是透明的，一旦价格发生变动，其他交易者可能会采取行动，LP 也会注意到这一点，并可能添加或移除流动性。添加或移除流动性的操作在另一次交易发生时再次产生不同的价格影响。价格影响开始影响价格影响，它在本质上变得 自我参照 。最简单的非线性和自我参照的模型称为 逻辑映射（logistic map） ，它产生了 混沌 。

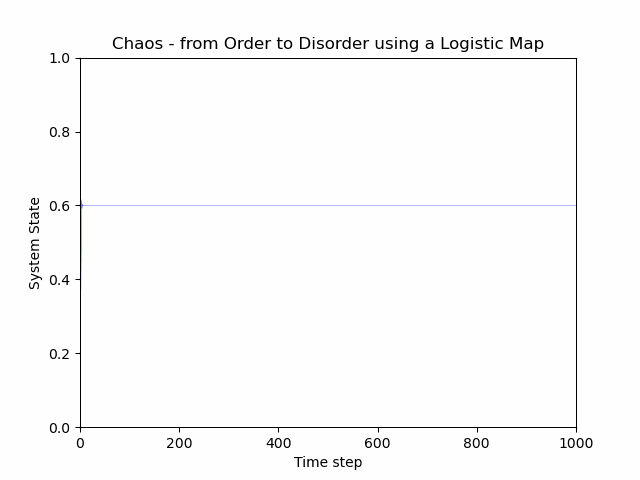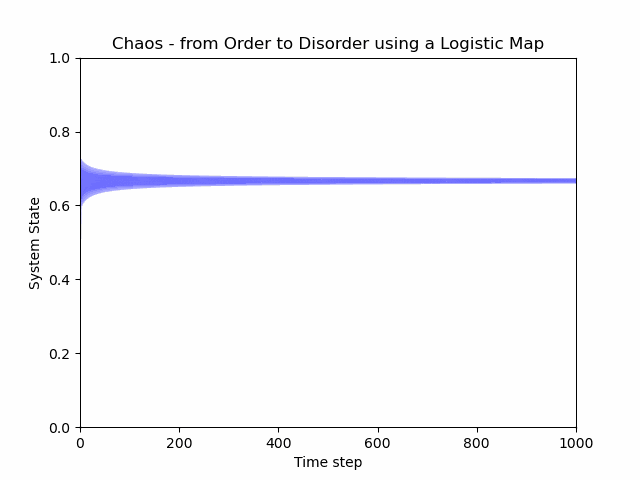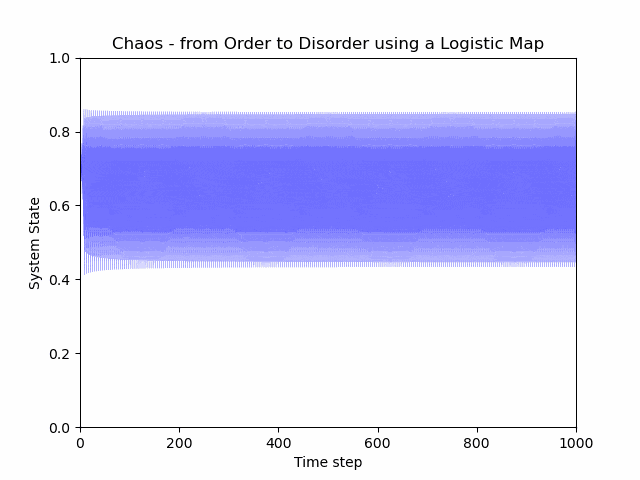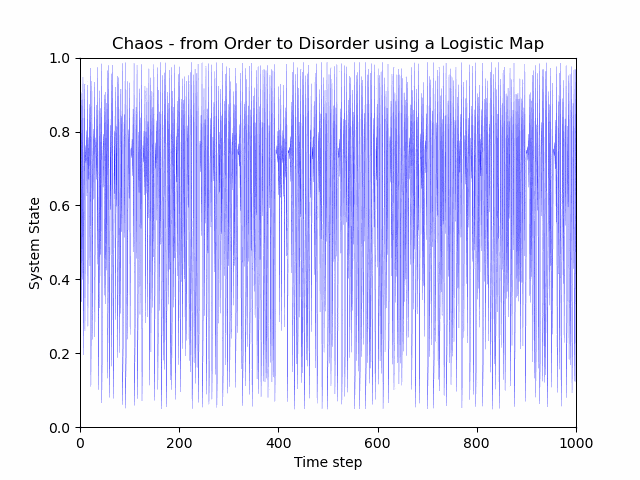一个非线性函数在自身上形成循环，导致混沌: https://en.wikipedia.org/wiki/Logistic_map

需要注意的是，尽管这个系统存在混沌，但我们仍然有系统重新访问循环点的时刻。让我们使用循环图来看一看，当我们增加逻辑映射方程 x[n+1] = rx(1-x) 的特定参数 r 时会发生什么。

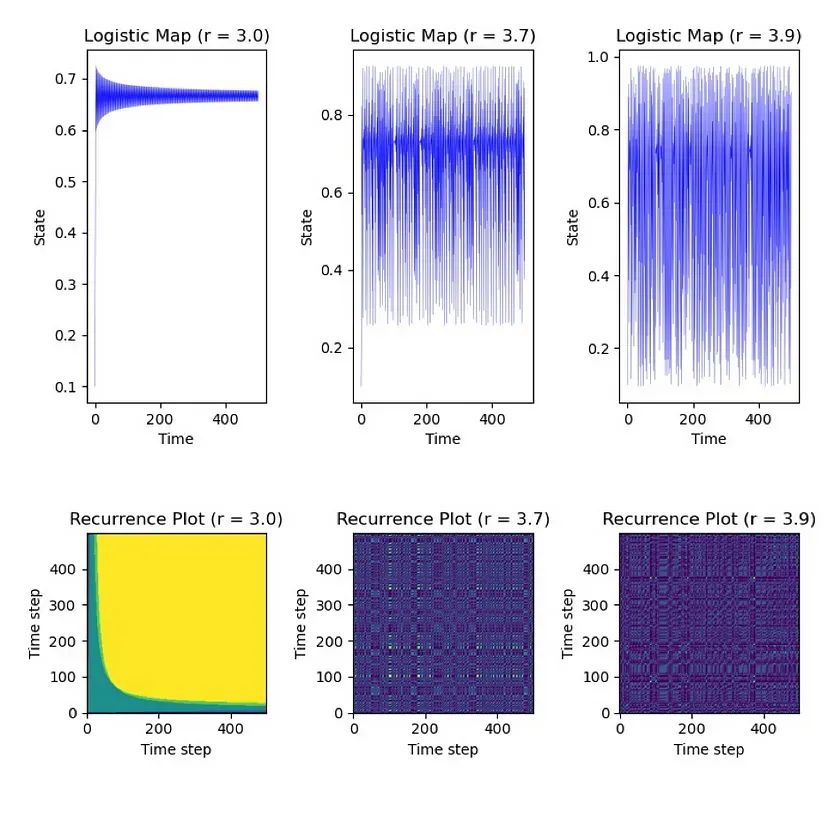尽管混沌已经开始，我们仍然观察到在右下方有明亮的区域。

观察如何循环不完全消失。我们仍然保留一些黄色区域，因为系统在自身循环中循环，显示即使在混沌系统中，我们仍然可以接近我们开始时的参考点。这会引起 LP 的兴趣。考虑到混沌的本质，让我们来看一个复杂的非线性系统，比如加密货币，以一个实时的例子。

2.3 - 循环的现实

当我们看 ETH/USD 自 2017 年以来的情况时，我们发现循环图仅在熊市期间亮起来。

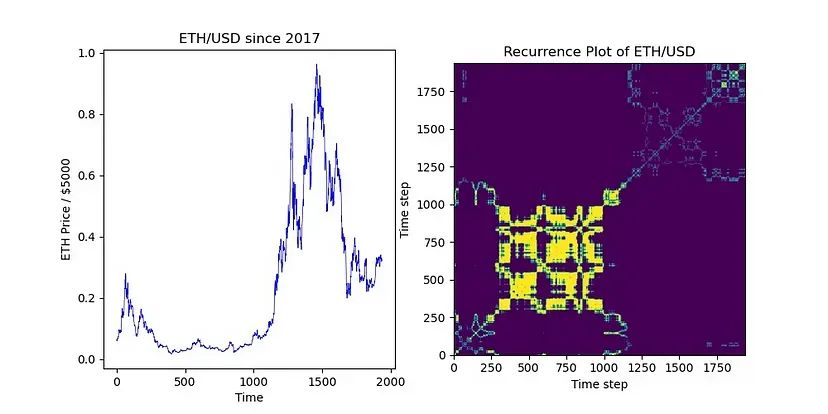
再现图大多是暗淡的。难怪 LP 们对于 ETH/USD 有困难，因为计价货币（分母）是一种稳定币。在这些情况下，需要使用更先进的模型，如 ARIMA + GARCH 来预测 ETHUSD（但这是另一篇文章的内容），并且必须使用频繁进出的较短时间段。相反，对于中性和被动的 LPing，我们可以看看计价货币与 X 代币漂移的池子。让我们来看看最大的这样的案例—— ETH/BTC。

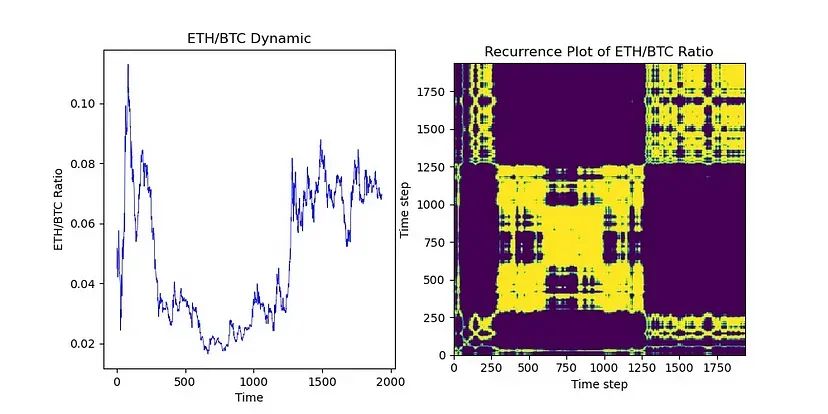
立即点亮循环点（如果您想玩下循环图代码，请参阅附录）。我们可以看到在 250-1250 和 1300-2000 之间存在大量循环！

但 LP 可能会担心 ETH 和 BTC 同时下跌。例如，我们可能会遇到像 COVID 这样的冲击，影响 ETH 和 BTC 的价值。在这种情况下，我们可以再次使用我们方便的循环图，找到一个组合，使两个代币一起漂移，也不会下跌 — 稳定币。让我们来看一下下面的 USDC/USDT 循环图。

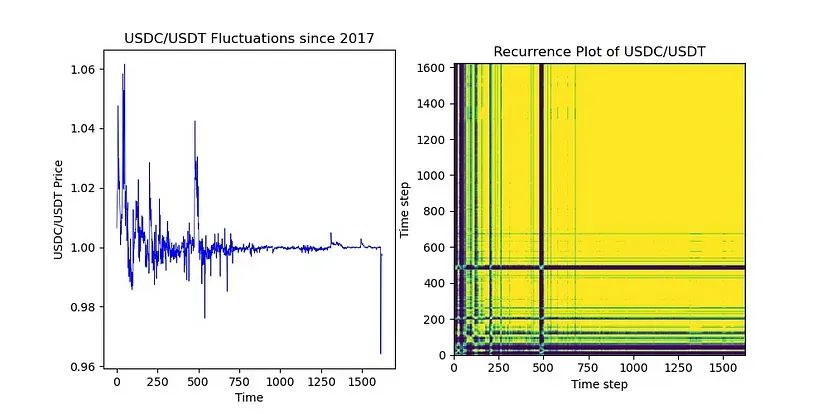
我们发现存在很多的循环。在这种情况下，我们可以利用这一点来将流动性集中到 Uniswap v3 中。

3 - 使用 Uniswap v3 进行最佳范围选择

当我们将上下边界（也称为 P_b 和 P_a 或简称为 b 和 a ）集中在一起时，我们实际上是加深了LP收益结构的“山峰”，在极端情况下将分散的“山峰”转化为悬崖。这得益于 Lambert 的 desmos 文件：

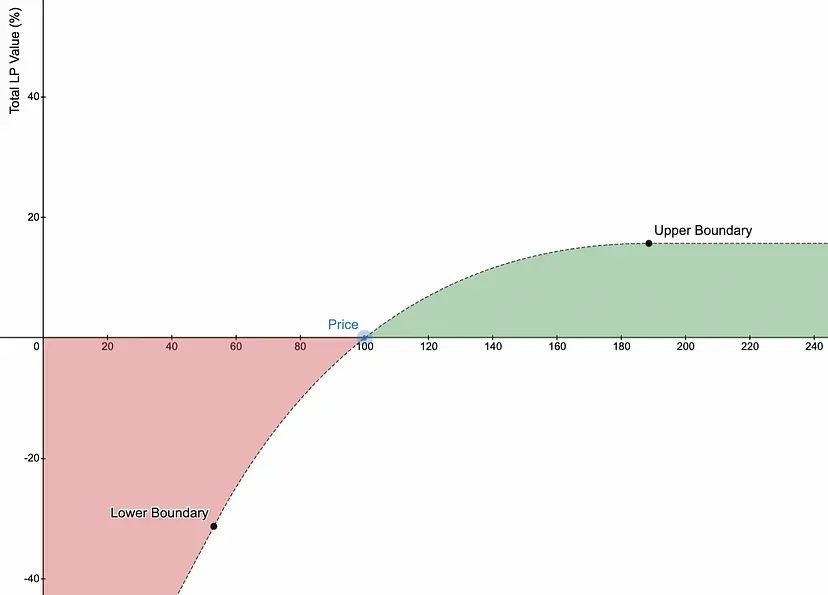宽波动边界导致价格波动时流动性提供者（LP）价值的平稳变动。

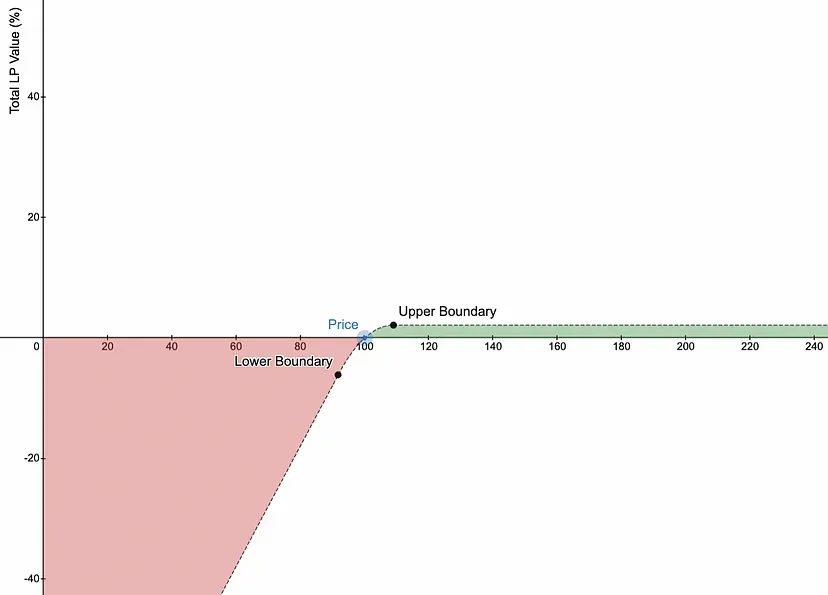高度集中的界限会导致悬崖般的形状。持有这样的头寸时间越长，就越有可能超出界限，无法获得任何 LP 费用。

考虑到边界约束，我们必须选择一个最优范围，以确保在尽可能高效地利用资本的同时平衡最大可能范围，以便仍然可以收取费用。Hayden Adams针对 Uniswap v3 提供了一种资本效率的公式。

关于上述公式的推导，可以看Lambert的链接：https://twitter.com/guil_lambert/status/1507163985531047938

如果我们将下边界价格（P_a）和上边界价格（P_b）同时以 百分比 x 移离当前价格：

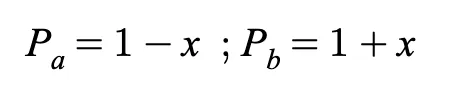
我们将这个公式重写为：

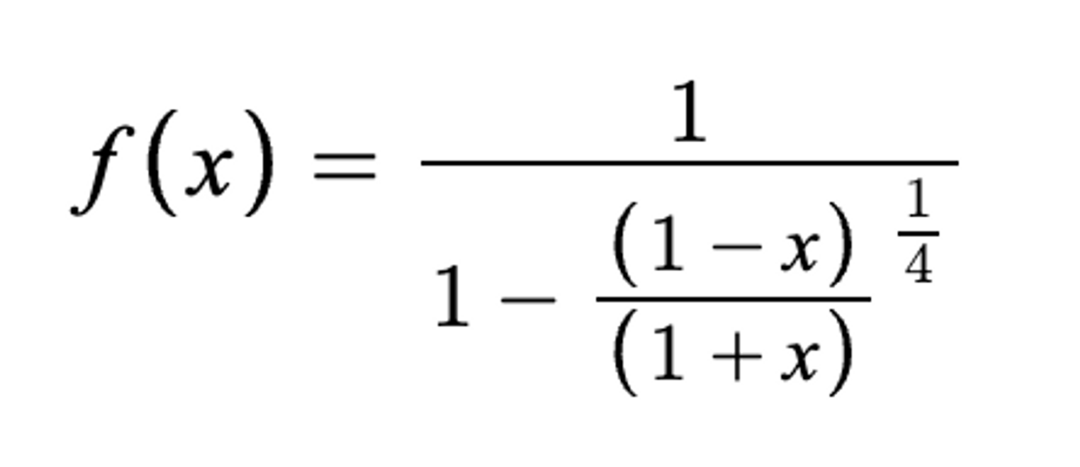
对函数进行x求导：

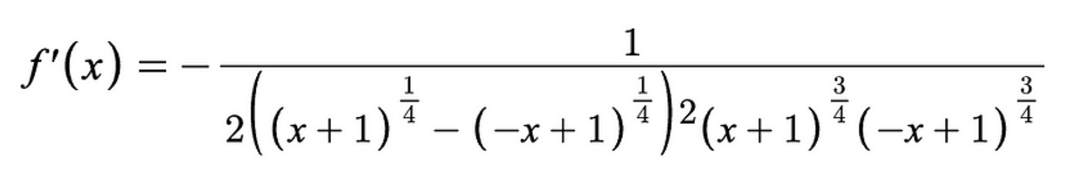
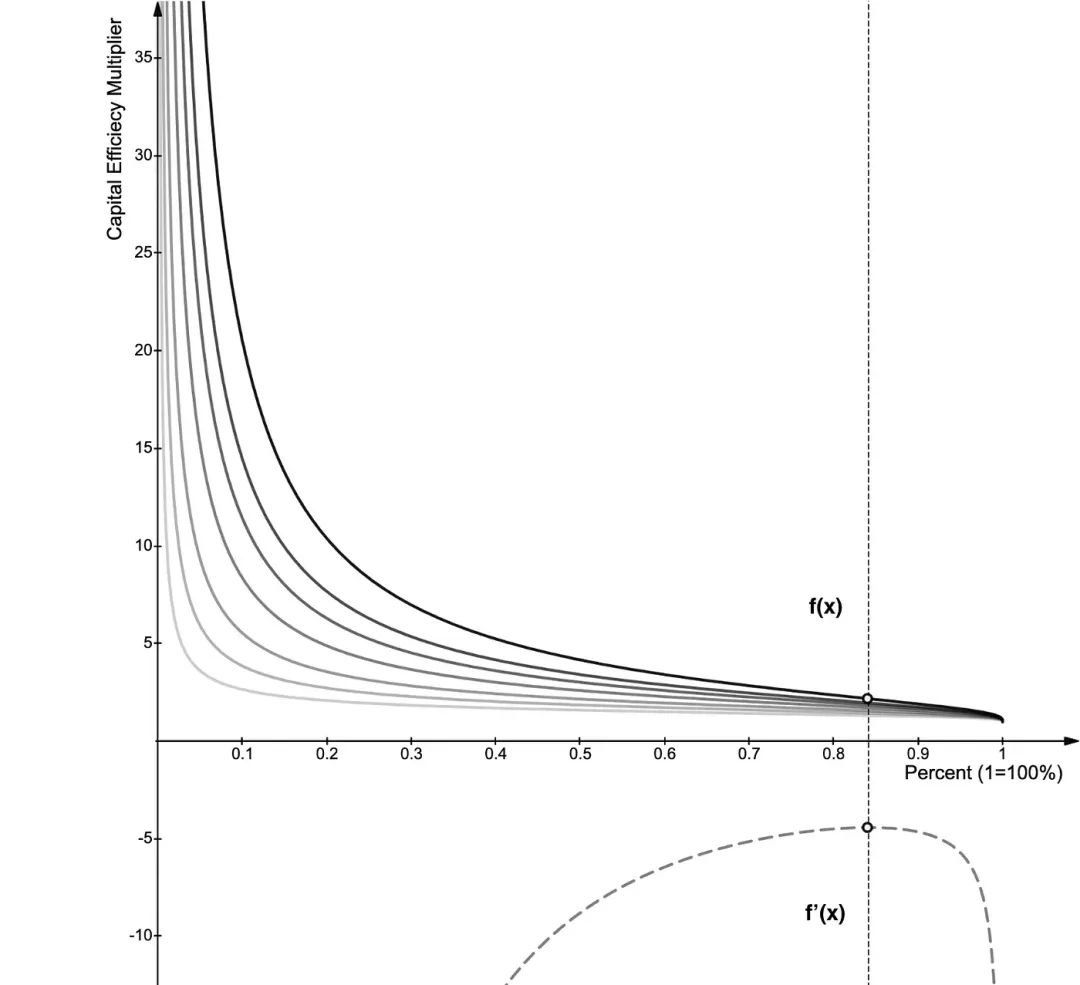
我们可以绘制这种关系图并注意到 f’（x）在84％时有一个峰值 ，资本效率为 2.18x 。这到底是什么意思？这意味着只要我们在 +/-84％ 的范围内，我们就可以使用大约两倍少的资本。

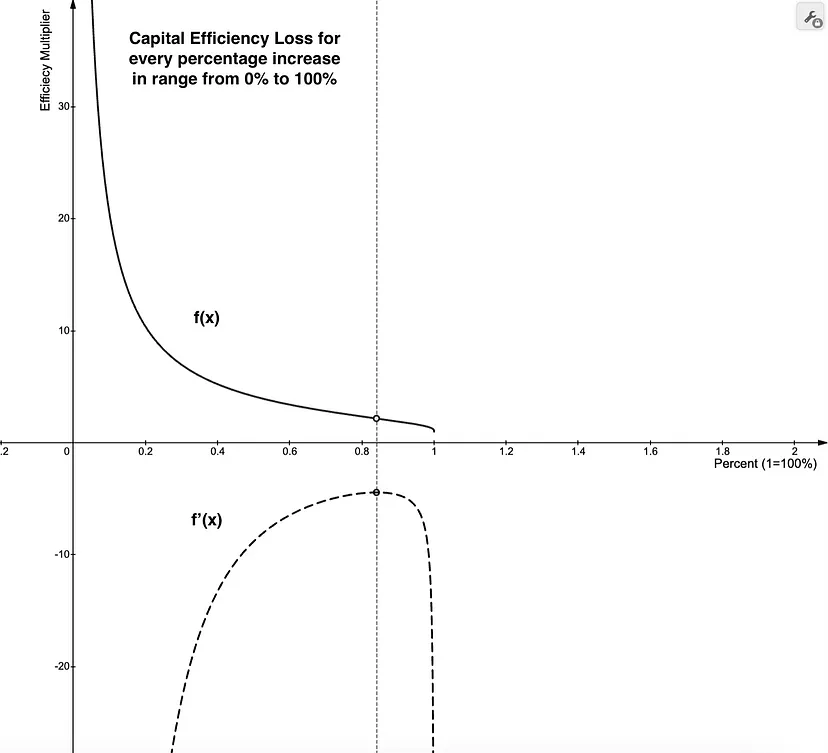Desmos交互链接：https://www.desmos.com/calculator/ysv2j74j6k

这也意味着，当我们开始增加上下边界以尽可能多地捕获范围时，我们会发现如果我们不确定价格走势，超过 84％ 变得微不足道。对于每超过 1％ 的增加，我们获得的回报越来越少，相反，84％ 成为平衡价格逃离边界和资本效率的 LP 策略的极限。

这种保守策略对于担心快速价格波动同时接收 LP 奖励的 LP 可能是有意义的。请注意，这种策略不旨在最大化费用，而是确保在尽可能少的资本的同时保持在范围内。

• 在第2部分与后续部分将持续发出。

• 如果您觉得这很有教育意义，请随意在Twitter上关注这只刺猬：@CK_2049

免责声明：请注意，为了努力弥合中英文信息差，这篇文章从 Medium 上翻译而来，详细的英文原文请查阅以下链接。我们也欢迎您关注我们的账号 zelos-research。本研究仅供一般信息目的。Uniswap 基金会很慷慨地赞助了这次私人研究的出版。它不构成投资建议或买卖任何投资的建议或招揽，并且不应用于评估做出任何投资决策的优点。不应依赖它作为会计、法律或税务建议或投资建议。本文反映了作者当前的观点。这些意见可能会随时更改而不进行更新

原文链接：https://medium.com/@med456789d/uniswap-v3-math-insights-part-1-of-6-f85e1597b411
关注 zelos-research：https://medium.com/zelos-research
我们的 github 仓库：https://github.com/orgs/zelos-alpha/repositories

附录

循环图的 python 代码：

import math
import numpy as np
import yfinance as yf
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.animation as animation

datausdc=yf.download("USDC-USD", start="2017-01-01", end="2023-04-21")
datausdt=yf.download("USDT-USD", start="2017-01-01", end="2023-04-21")

data3=datausdc/datausdt

dat=data3['Close']
dat = pd.to_numeric(dat, errors='coerce')
dat=dat.dropna()

x = np.array(dat.values)

fig, (ax1, ax2) = plt.subplots(nrows=1, ncols=2, figsize=(10,5))

# Plot the time series in the first subplot
ax1.plot(range(len(x)), x, 'b-', linewidth=.5)
ax1.set_xlabel('Time')
ax1.set_ylabel('USDC/USDT Price')
ax1.set_title('USDC/USDT Fluctuations since 2017')
n_end=len(x)

# Create a recurrence plot in the second subplot
R = np.zeros((n_end, n_end))
for i in range(n_end):
    for j in range(i, n_end):
        if abs(x[i] - x[j]) < 0.01:
            R[i, j] = 1
            R[j, i] = 1
ax2.imshow(R, cmap='viridis', origin='lower', vmin=0, vmax=1)
ax2.set_xlabel('Time step')
ax2.set_ylabel('Time step')
ax2.set_title('Recurrence Plot of USDC/USDT')

# Display the plots
plt.show()
plt.savefig("usdc/usdt.jpg", dpi=100)

发散损失的简单推导：

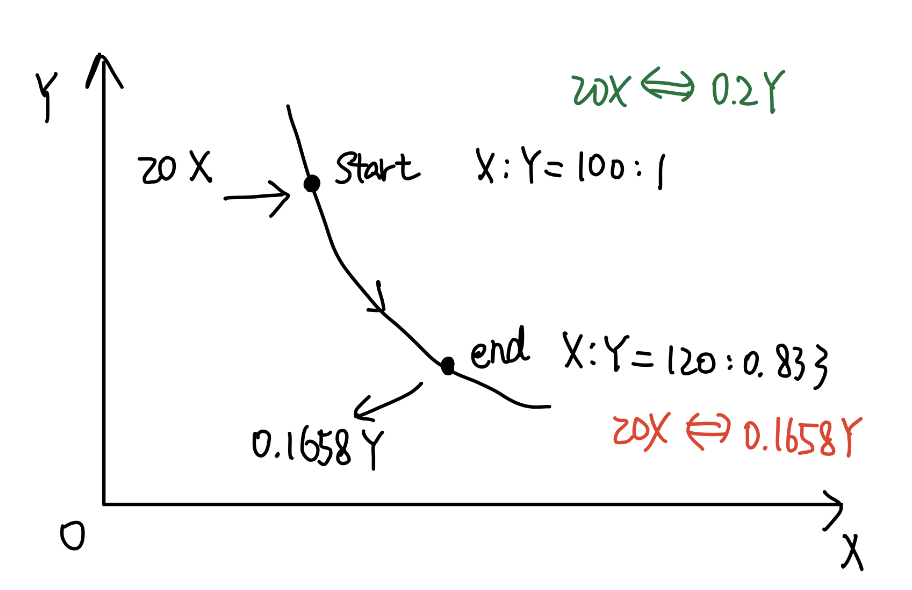
以进入时价格为 X:Y=100:1，退出时为 X:Y=120:0.833 为例，起初 20X 能兑换 0.2Y，由于发散损失，在退出时，资产价格损失使得 20X 只能兑换 0.1658Y

推荐阅读

Uniswap v3 数学洞察系列翻译 —— 第一部分 共 6 部分
Uniswap v3 数学洞察系列翻译 —— 第二部分 共 6 部分 Uniswap v3 数学洞察系列翻译 —— 第三部分 共 6 部分 Uniswap v3 数学洞察系列翻译 —— 第四部分 共 6 部分 Uniswap v3 数学洞察系列翻译 —— 第五部分 共 6 部分 Uniswap v3 数学洞察系列翻译 —— 第六部分 共 6 部分