Uniswap v3 数学洞察系列翻译 —— 第四部分 共 6 部分

本文翻译自 https://medium.com/@med456789d/uniswap-insights-part-3-of-6-f49aa1e5523c，原系列标题为  Uniswap v3 Math Insights ，共有六部分，此为第四部分，该篇主要介绍期权如何与头寸结合，需要对该系列之前所述的头寸策略有一定了解。

为了让更多人可以访问和了解关于 Uniswap V3 的有用信息，我们翻译了系列文章，让中文读者对 Uniswap v3 机制和投资策略选择有更深入的理解。在阅读本翻译同时，可以随时参考原文以获取更多详细信息。

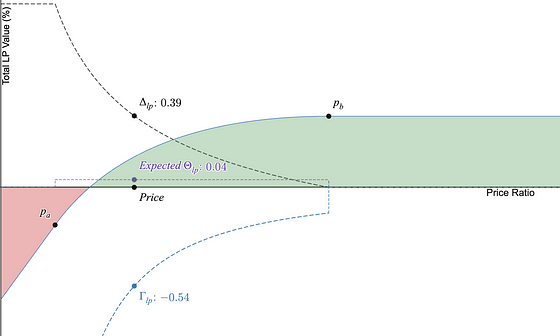LP头寸表现出凹性（也称为负凸性）-价格下跌时加速下降，价格上涨时放缓增长。

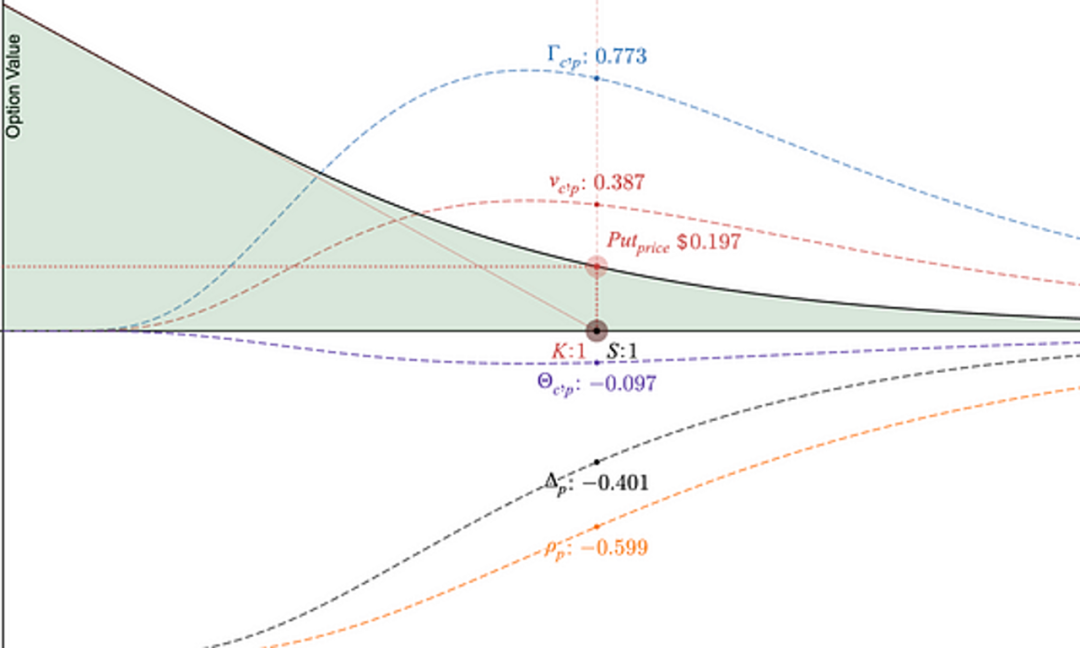
看涨期权表现出凸性 - 价格下降时加速攀升，价格上涨时放缓下跌。

简而言之：
主要有两种简单的对冲 LP 头寸的方法和一种复杂的方法：

1. 借用基础资产 ，但这并不能取消凹形，因为仍然会保留一定程度的发散损失。

2. 借用相似的LP头寸 ，在这里可以摆脱凹性，但是还没有为定制LP头寸提供流动性市场。

3. 将 LP 头寸与看跌期权结合 。在这里，可以暂时取消凹性，但是随着时间的推移，发散损失会产生。需要重新滚动期权以维持 LP 对冲。

看起来没有免费午餐，只有权衡取舍。

1. 借用基础资产

与其将 100% 分配给 LP 头寸，不如将部分分配给 X 资产的做法，其余部分用于做空X资产以减少但不消除发散损失。结果是将支付结构从悬崖转换为山丘，如 Guillaume Lambert 所示：

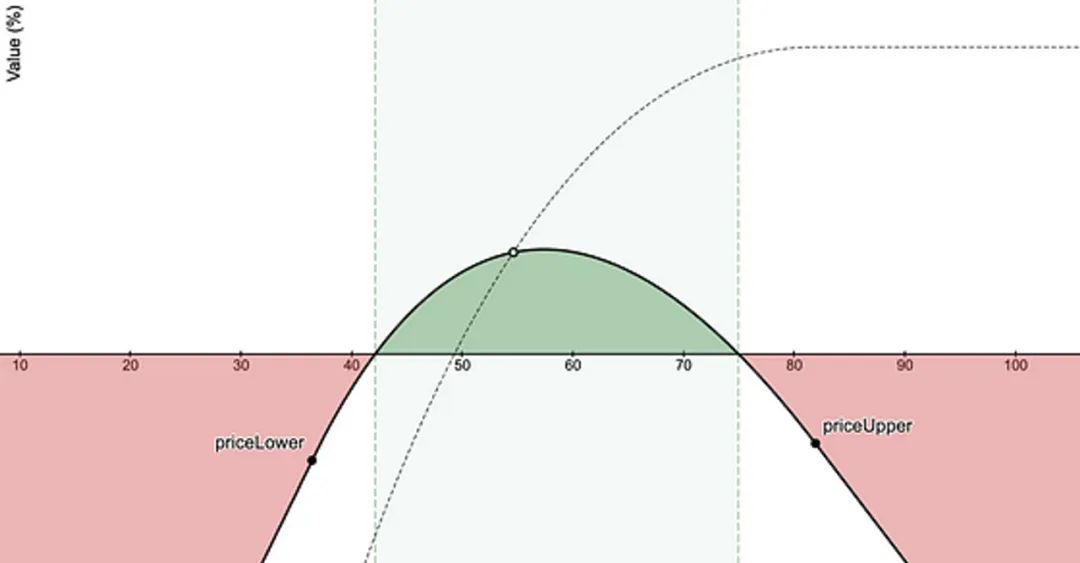
Guillaume Lambert 用于组合短 + LP的desmos文件：https://www.desmos.com/calculator/669zg1rmvb
Atiselsts.eth 还提供了一种动态对冲的方法，涉及随着价格变动的频繁买卖：https://atise.medium.com/liquidity-provider-strategies-for-uniswap-v3-dynamic-hedging-9e6858bea8fa。这是一种非常有趣的方法，但在主网上进行动态对冲将消耗大量费用，因此第 2 层实际上可以为 LP 提供有用的目的，但要注意，较低的费用通常是以集中化的代价为代价的，正如我们最近看到的 Arbitrum 的错误导致 L2 停止处理一样。

2. 借用LP头寸-更简单的方法

LP 头寸的本质是凹形的。使用下面的全范围 LP 头寸的基本交互式示例：

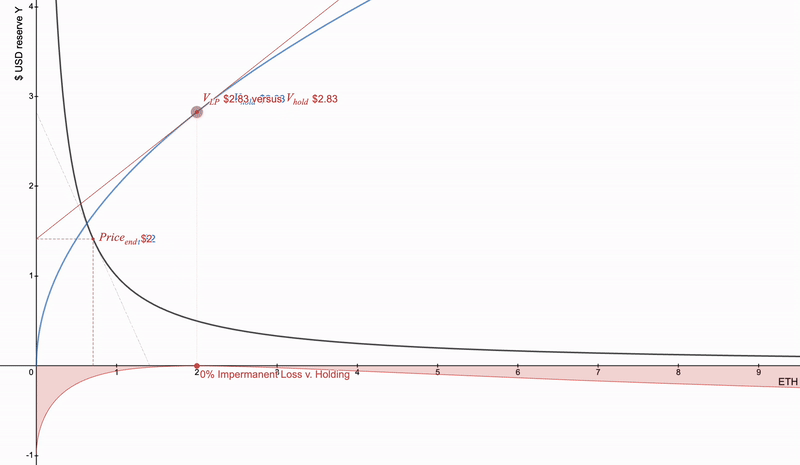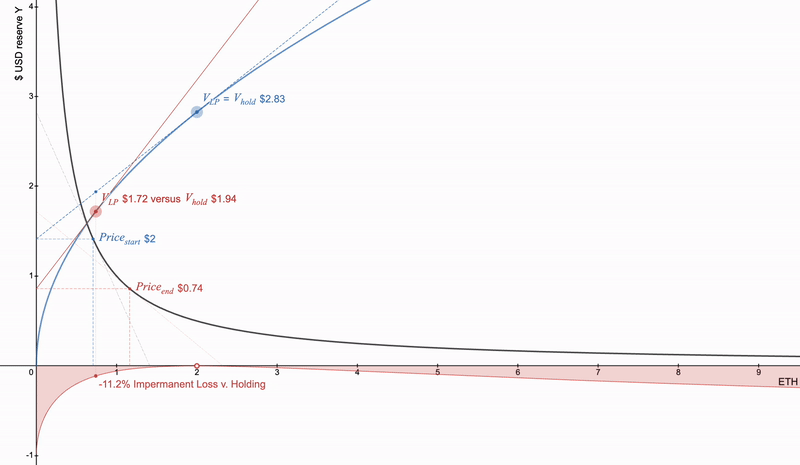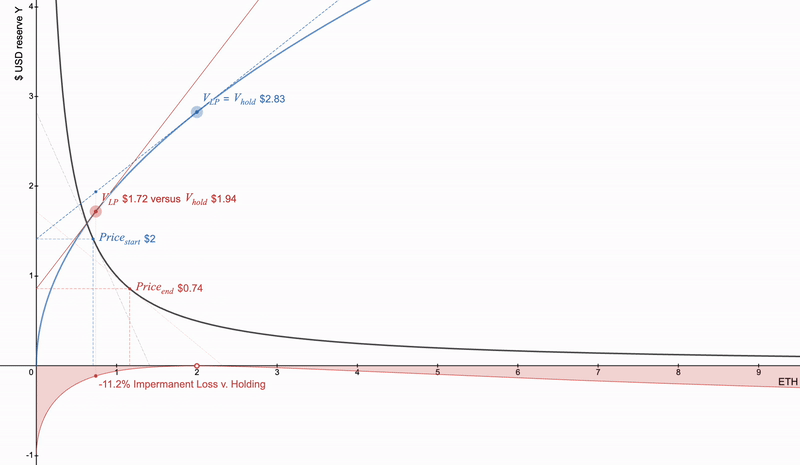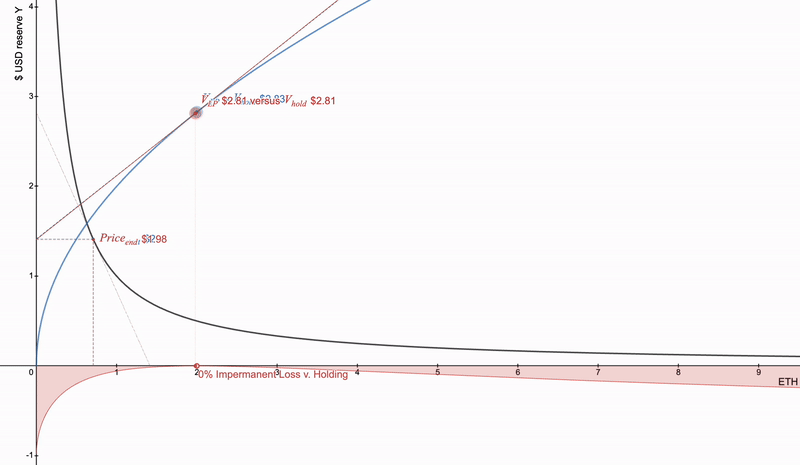
Uniswap全范围LP头寸价值为蓝色。红色为价格变化。在x轴下面的是LP和持有之间的发散。Desmos交互链接-https://www.desmos.com/calculator/cntuhfqang

如果主要资产价格下降，则损失加速。要取消它，可以借用这样的头寸，它将是完美的匹配。

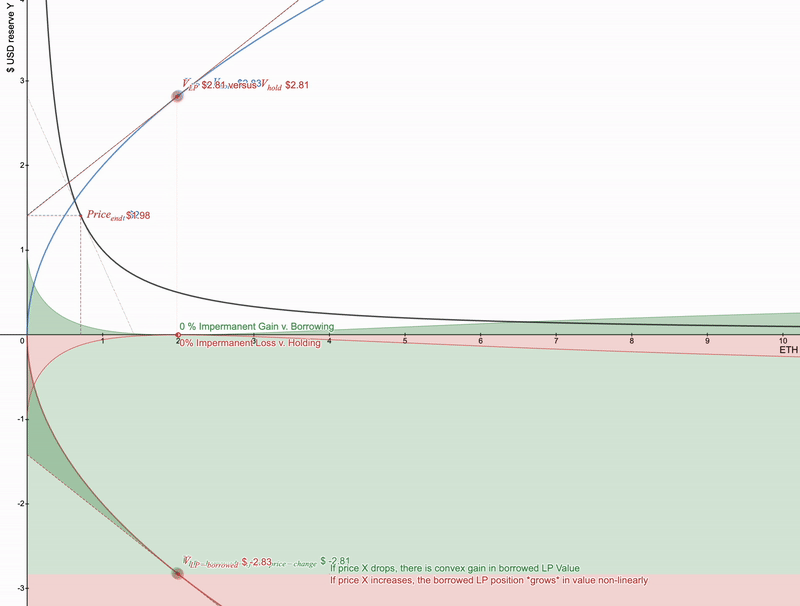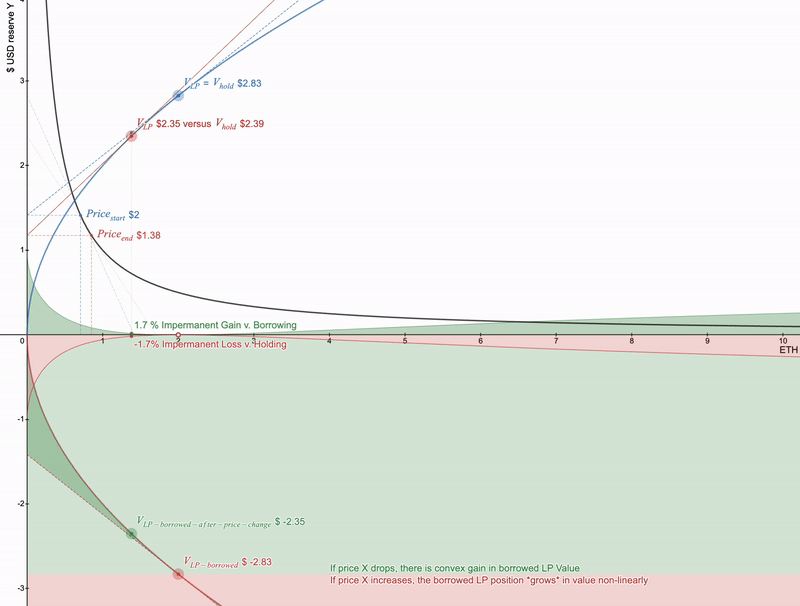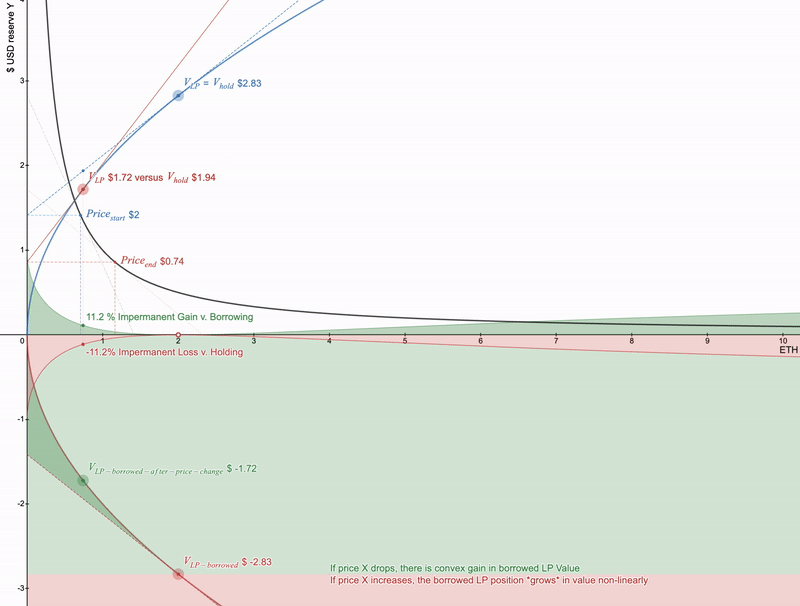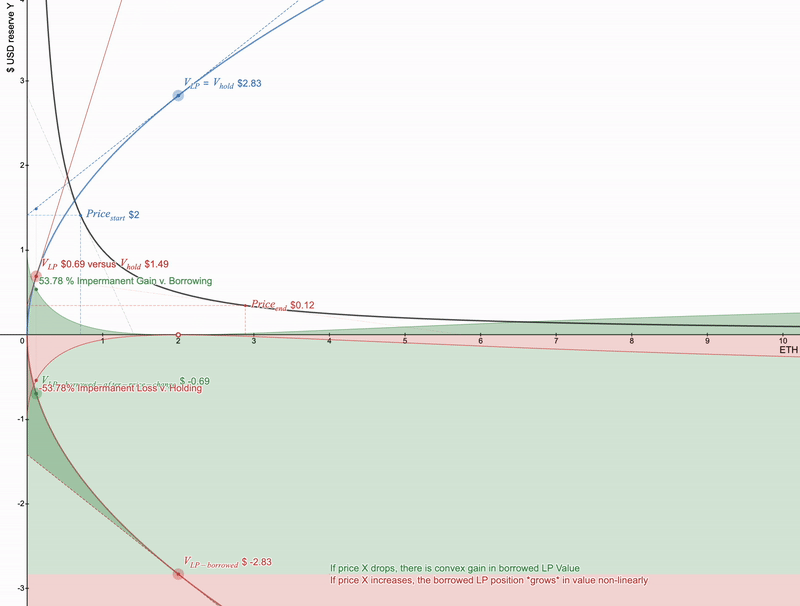
将“Borrow LP”按钮在Desmos中展示 - https://www.desmos.com/calculator/cntuhfqang

仅借用 LP 头寸就将支付从凹形转换为凸形，但请注意，如果 X 的价格 上涨 ，那么借用的 LP 头寸实际上会变得更加昂贵。

价格上涨会导致借用的全范围 LP 值增长。通过集中的流动性，可以将其减少。

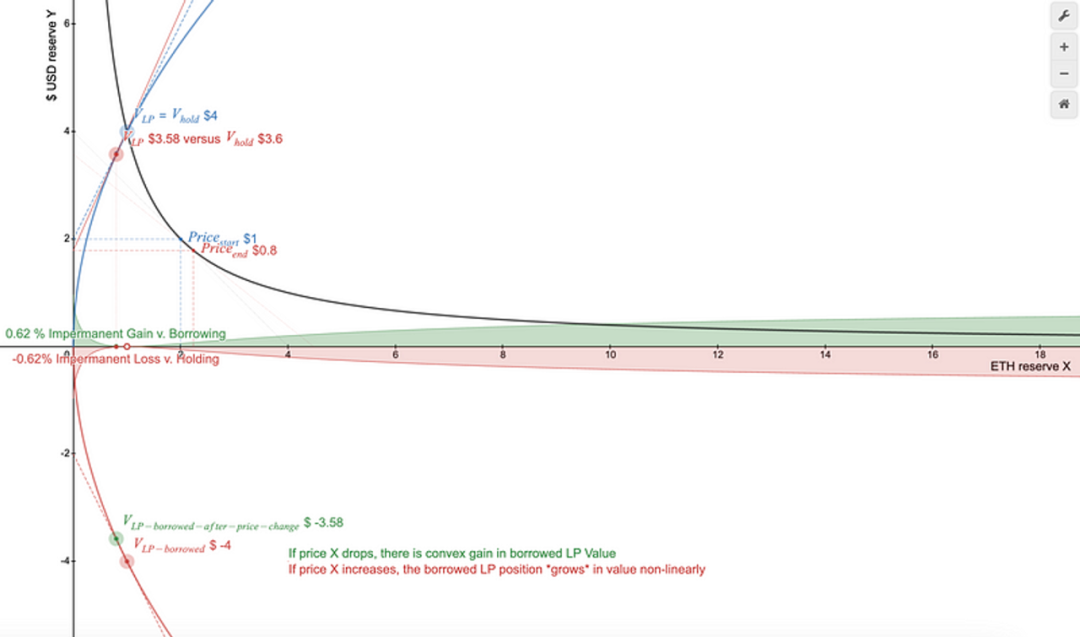
价格上涨会导致借用的全范围LP头寸价值增长。通过集中流动性，这种增长可以得到减少。

如果使用集中的流动性，就会在 p_a 和 p_b 之后创建线性支付。借用这些位置可以展现有趣的特性。这特别明显， 如果将借用基础资产与借用 LP 头寸相结合 。可以得出一系列有趣的支付：

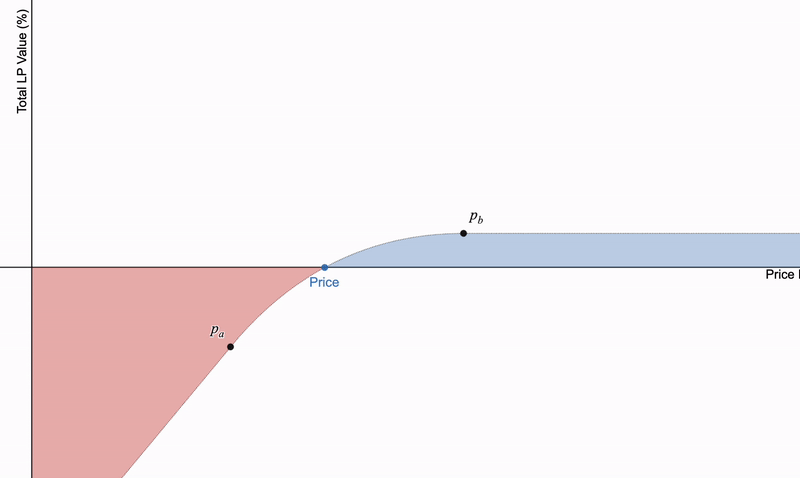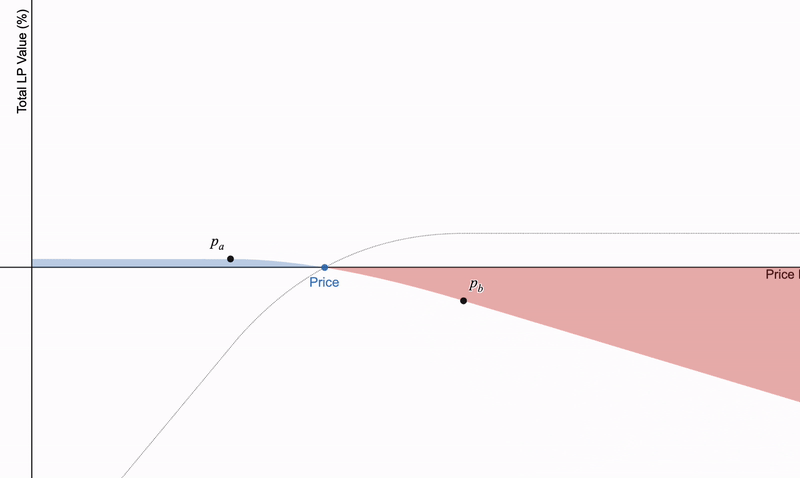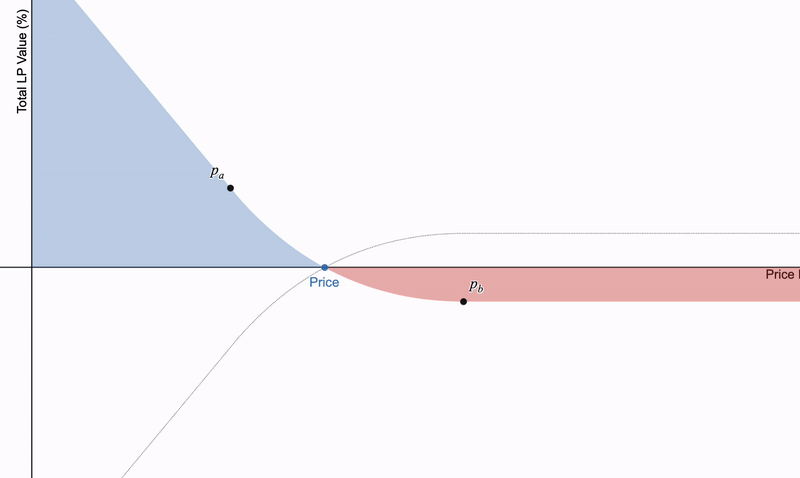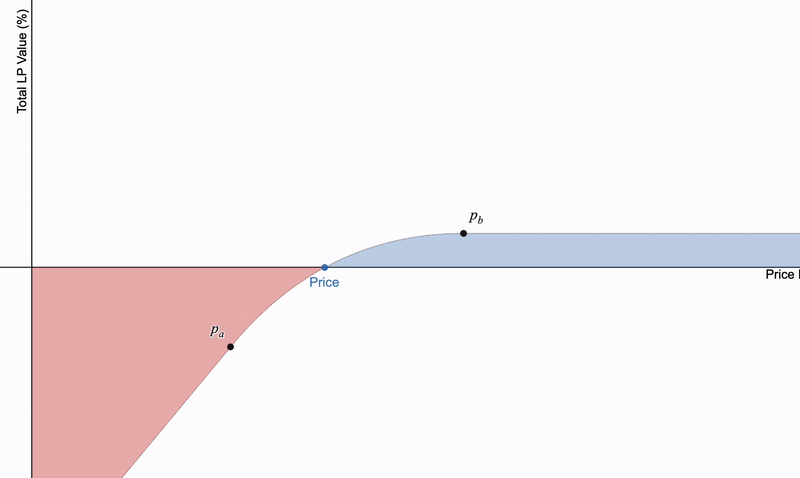
（1）长期持有 LP 头寸；（2）借用标的资产并持有 LP 头寸；（3）借用 LP 头寸并持有标的资产；（4）借用 LP 头寸并卖空标的资产。

我个人将这些合成组合称为 CPs—— 曲线永续合约，因为它们不会到期。当收益结构是凸的时候，它被称为 凸永续合约，也是 CP。当收益结构是凹的时候，它被称为 凹永续合约，同样也是 CP！

这样的合成 DeFi 原始组合与永续合约的关系可以通过看涨期权-看跌期权平价关系来解释。通过组合一个长凸永续合约和一个长凹永续合约，可以得到一个普通的长永续合约：

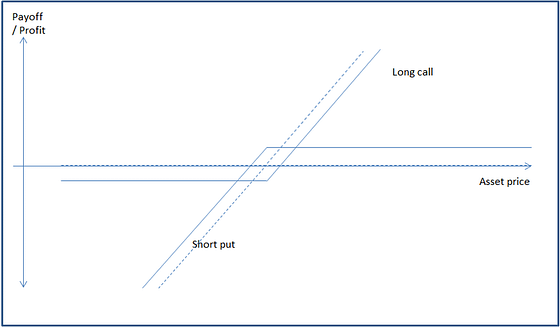这与将平价的看涨期权与看跌期权进行组合以复制一个标的资产（虚线对角线）的概念完全相同，只是用长期合约（Perpetual）来复制标的资产。

从交易成本和工程角度来看，理论上借贷和构建这样的 CPs 可能成本高昂且具有挑战性，但正如我写这篇文章时，已经有非常聪明的人在解决这个问题。但就目前而言，我们只能使用 Black-Scholes 期权模型来消除 LP 仓位的曲率。

3.将期权与 LP 头寸结合

为了理解 LP 对冲，我们必须了解“希腊字母”（金融指标），因为这些期权的衍生品使我们能够比较 LP 头寸和期权之间的支付。我们可以看到下面的所有希腊字母在期权到期时的视觉行为：

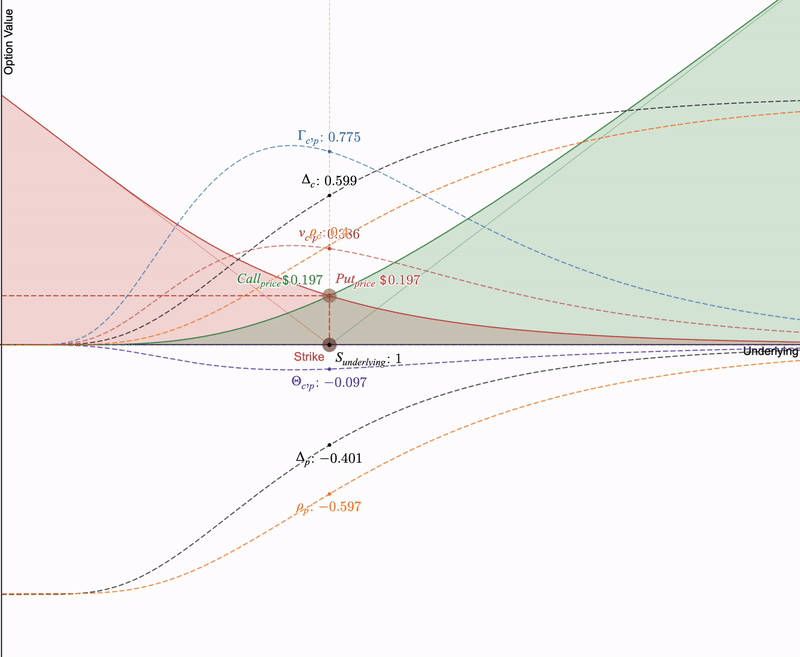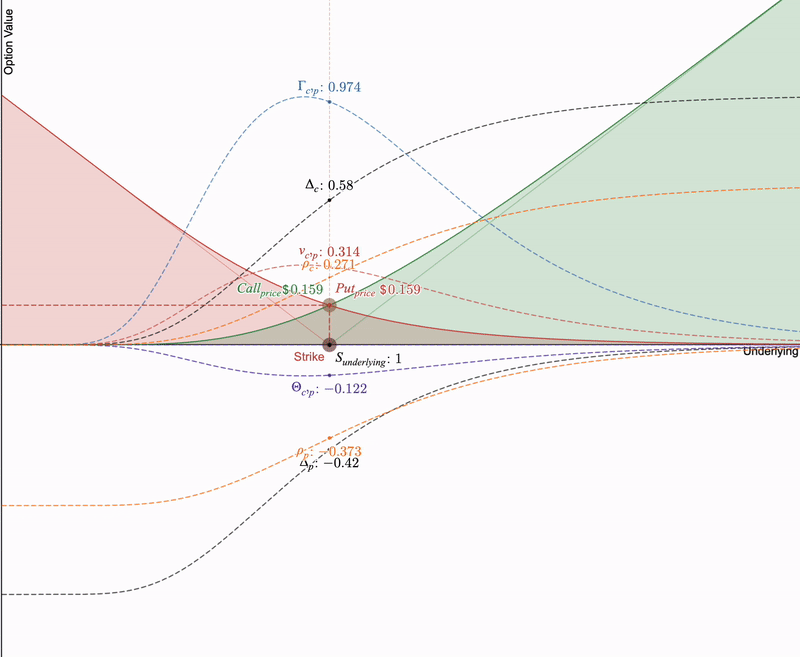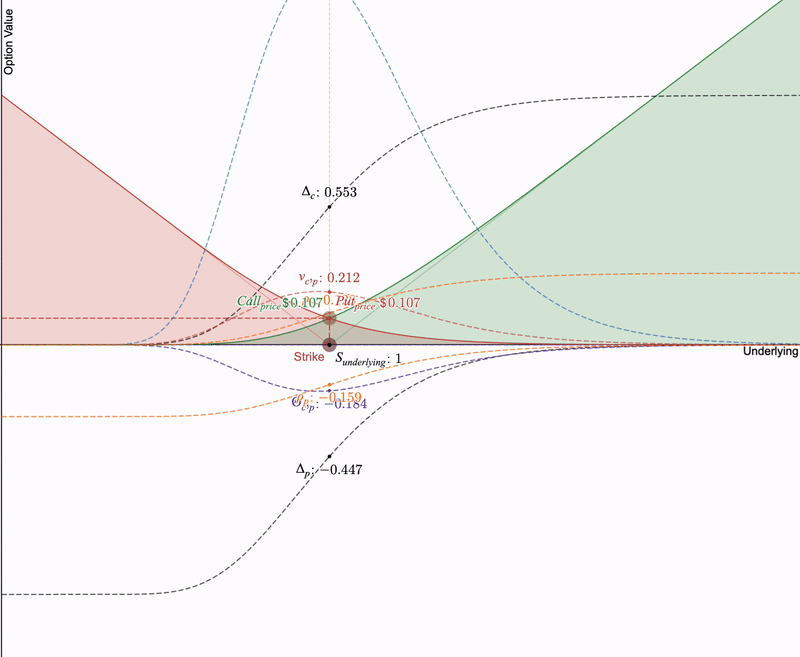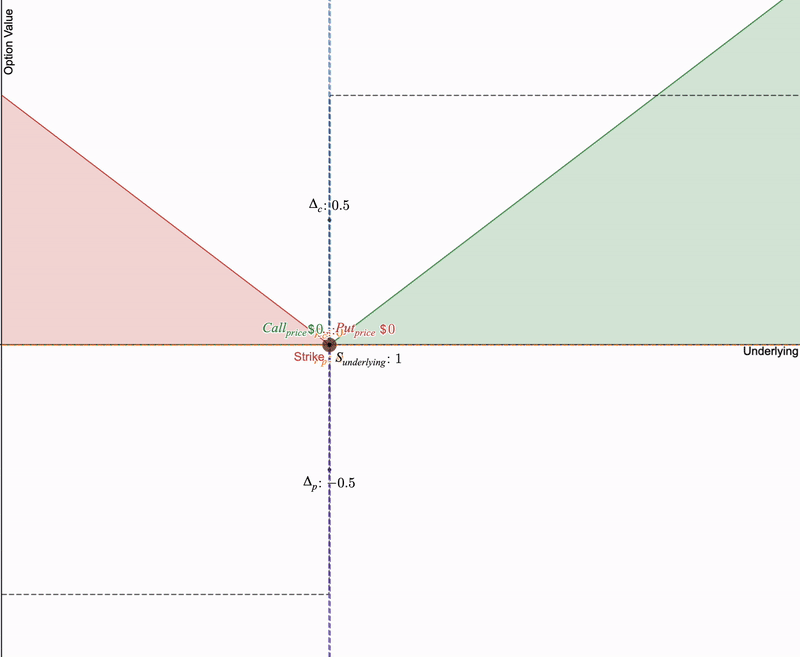
当期权在行权价格处到期时，看涨期权和看跌期权的价值都逐渐趋近于零。希腊字母也随之变化。Delta值越来越陡峭，Gamma值达到顶峰，Theta值加速下降至最低点。

我创建了一个交互式期权计算器，其中包含我认为对于不仅仅是这个受众而言的所有希腊字母都很有用的内容 - https://www.desmos.com/calculator/x5vk8qkweg

现在了解期权的主要希腊字母是 delta，gamma 和 theta，因为我们将开始将它们与 LP 希腊字母进行比较，然后进入 vega 和第 5 部分中的其他希腊字母。

我们将在此处仅涵盖前三个。

LP 通过费用获得 Theta，而期权买家则通过对冲支付 Theta。> 作为 LP，会通过费用得到 Theta 的补偿。
作为期权，您需要支付期权费用的 Theta 来获得凸性的特权。

对于我们的看跌期权，重要的是随着时间接近到期，期权的价值会以紫色的 Theta 捕获的加速方式下降。它变得更加敏感于快速价格变化（强调 delta 和 gamma），其红色形状变得更陡峭，因为其价值趋近于零。

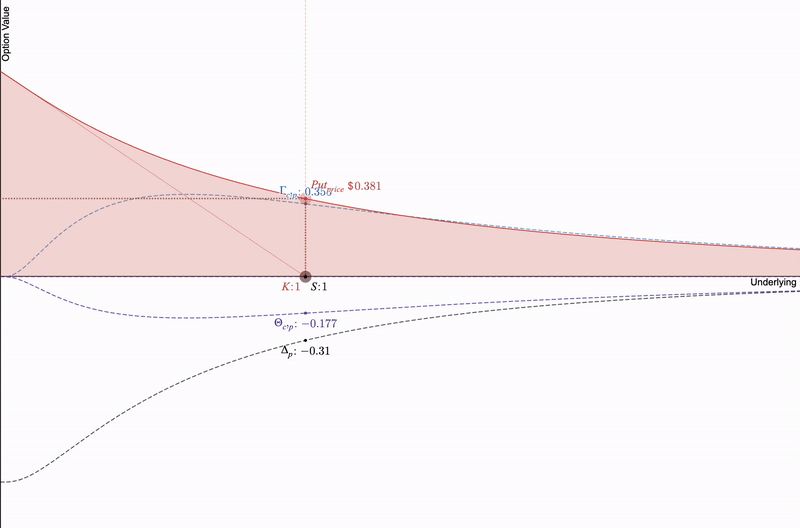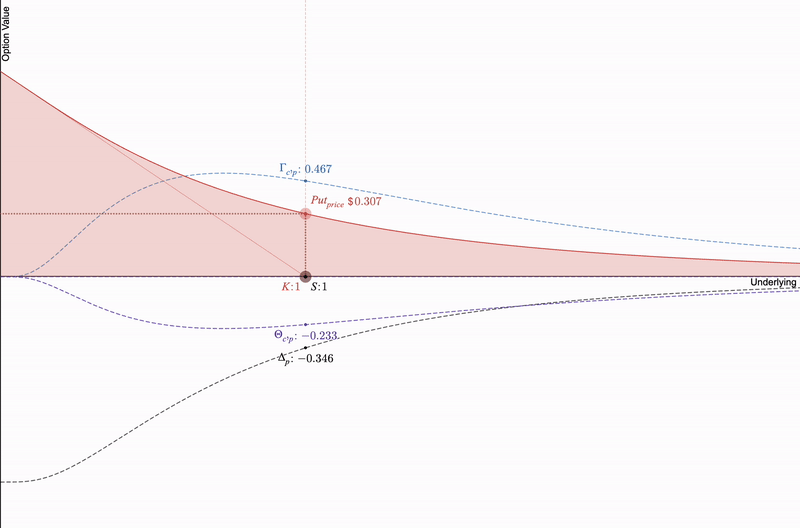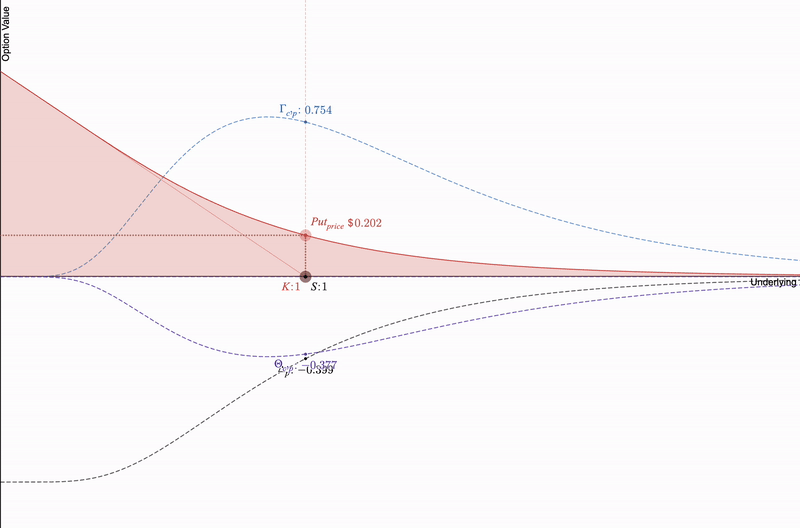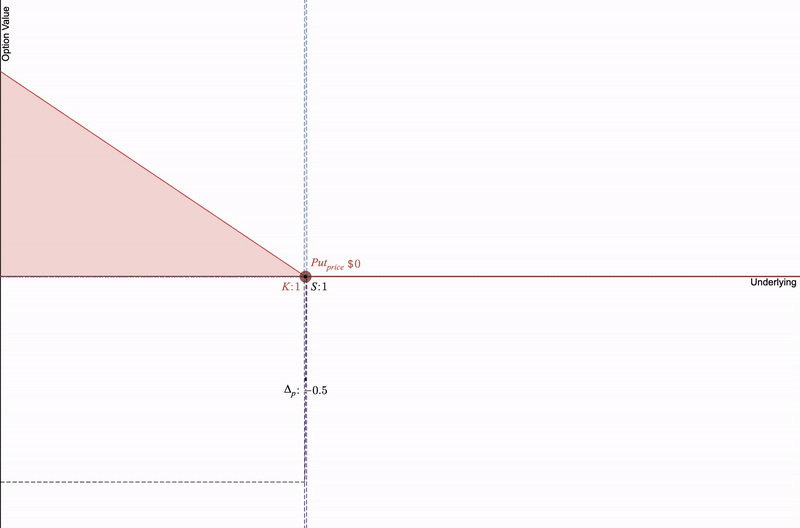
看跌期权接近到期。需要注意的是，Delta、Gamma 和 Theta 都会加速变化。

如果我们将这三个期权希腊字母与仅限制流动性头寸进行比较，当价格几乎不发生变化时，价格敏感的希腊字母（delta 和 gamma）在时间推移时大多固定，但以 LP 费用表示的 theta（严格为正）取决于池中的交易活动而有所变化：

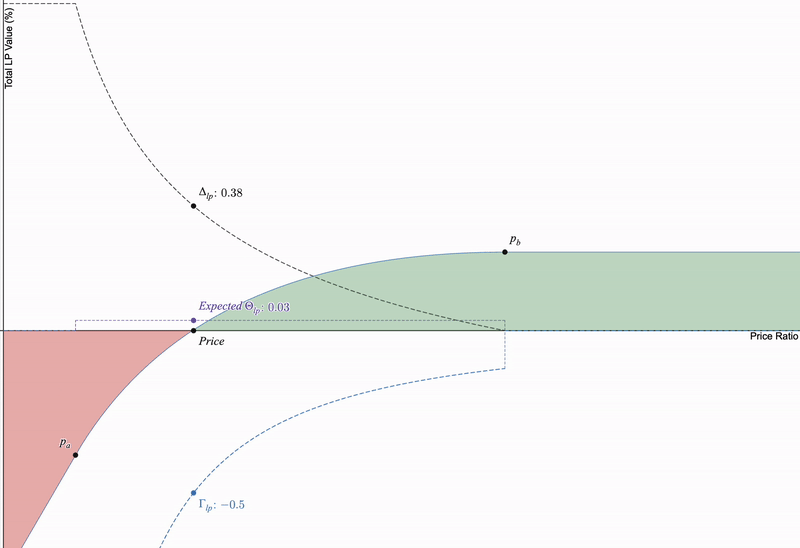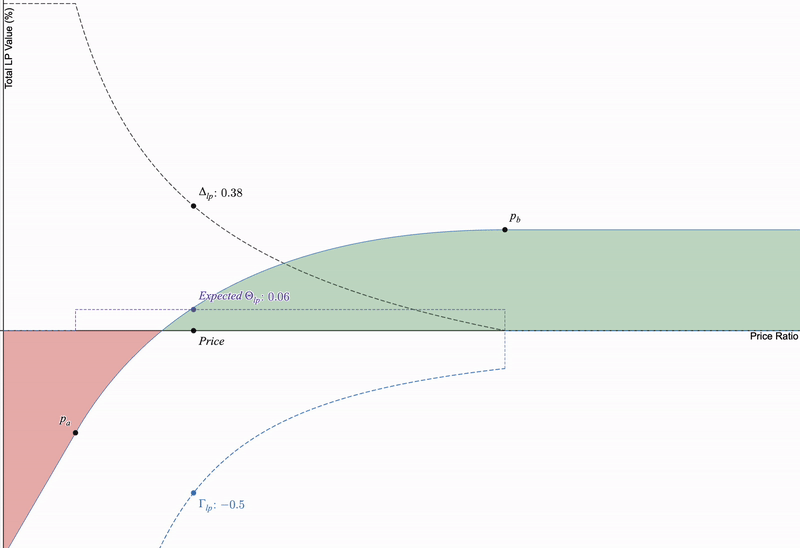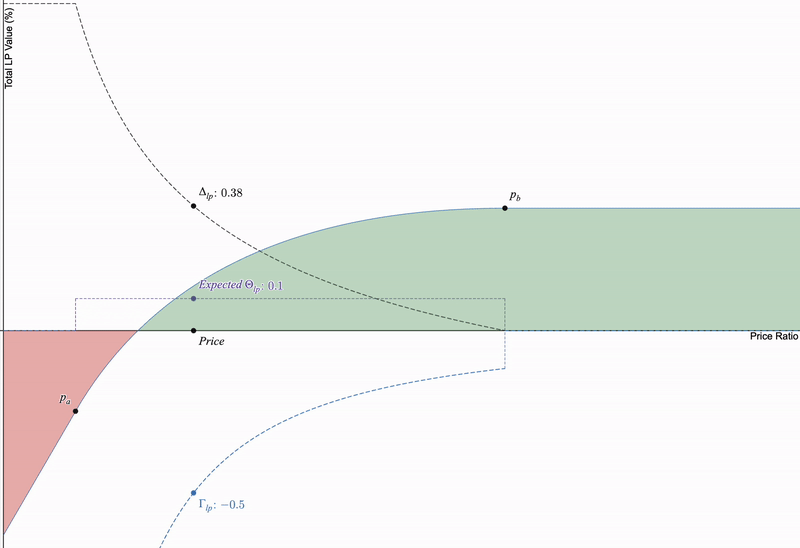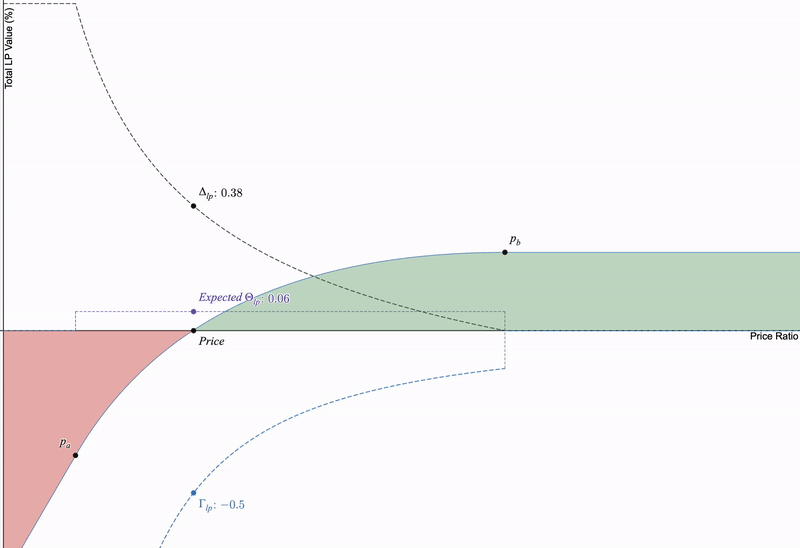
theta始终为正，但作为LP，它取决于交易量而有所变化。我将价格变动固定以便于可视化，以显示时间对delta和gamma没有影响。

如果放大，为了通过费用产生 Theta，价格本身必须具有小的刻度增量移动，因为如果底层交换中没有扰动，则无法产生费用，我们将损失 Theta。

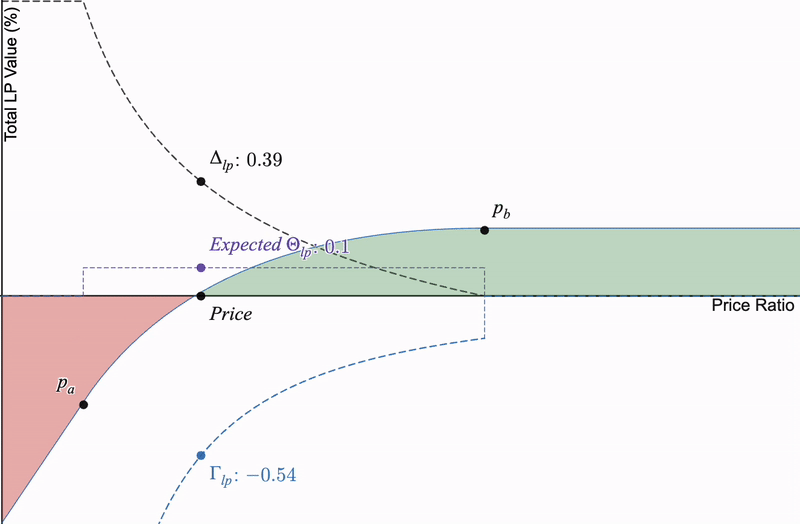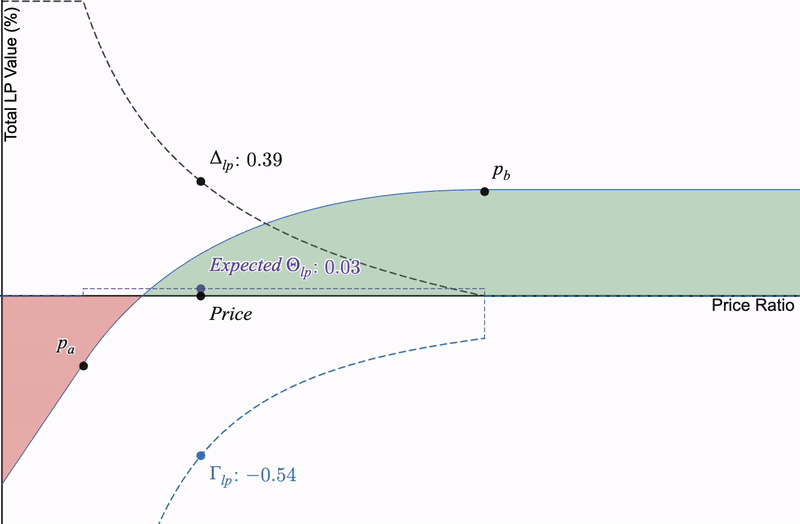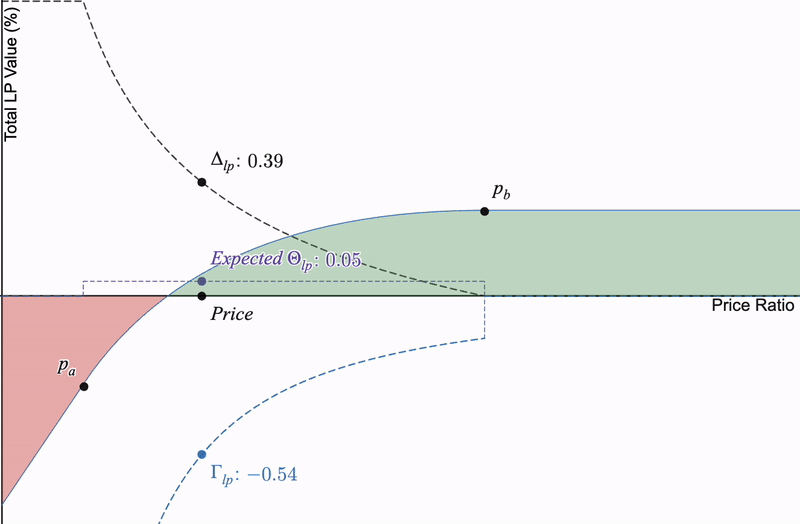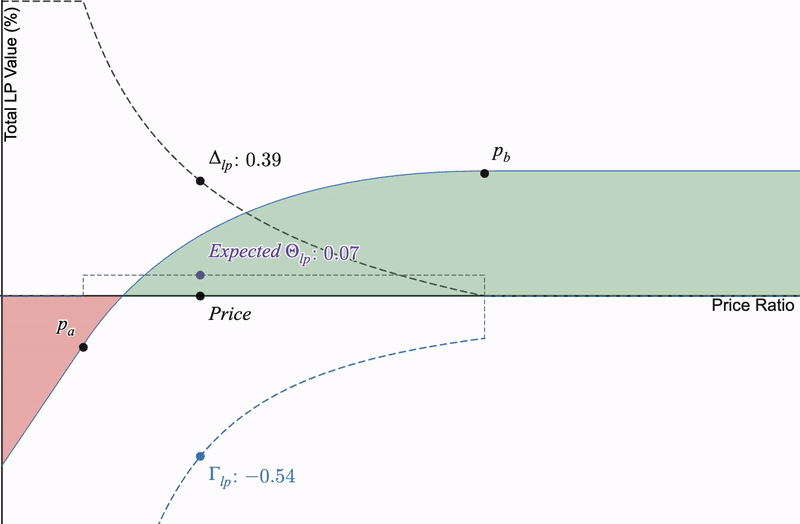
如果没有交易量>>没有交换>>预期Theta趋近于0

期权和 LP 头寸之间的三个希腊字母的巨大差异是由于 LP 头寸的非到期/永久特性导致 Theta 不匹配以及 xy=k 不变的性质导致 Delta 和 Gamma 不完全对齐。

如果我们尽可能接近将看跌期权与 Uniswap 的集中流动性位置相匹配，我们的 Delta 和其他希腊字母 大致 匹配，但它们不是 100％ 完美的（请参见黑线），我们也可以看到红色的看跌期权和蓝色的 LP 头寸的取消会有所不同：

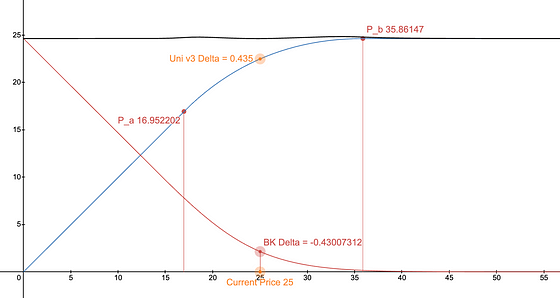最接近的看跌期权相对于LP Delta的-0.43 Delta。看跌期权和LP头寸之和应该是一个完美的黑线，但请注意它的轻微曲率。

如果某个资产的期权在 AMM 上没有交易量怎么办？则我们的 Delta 随时间推移而开始发散：

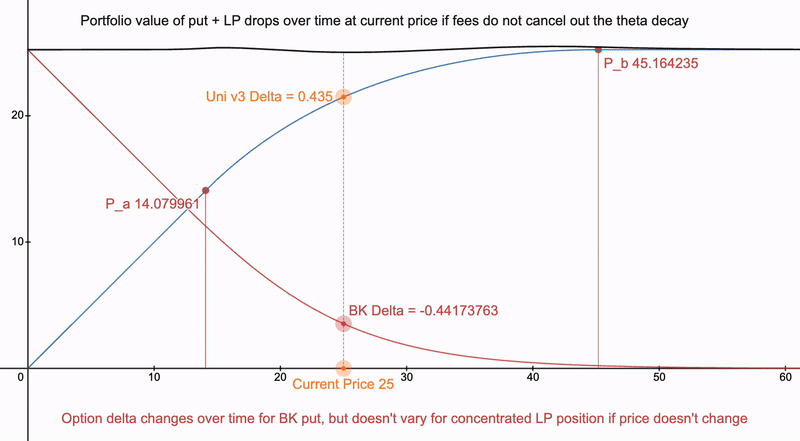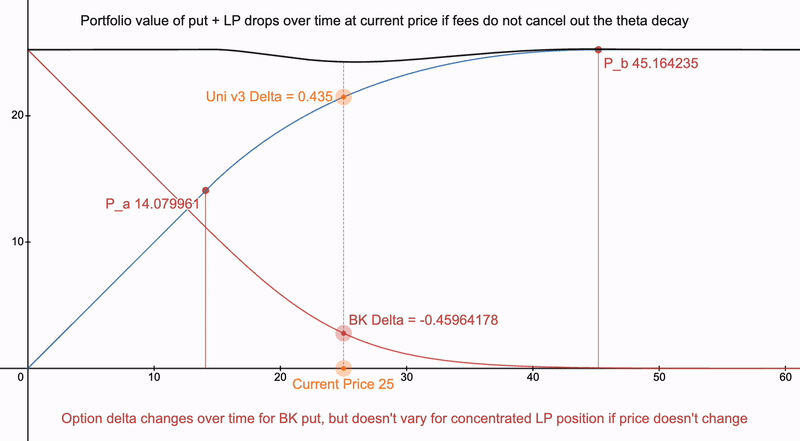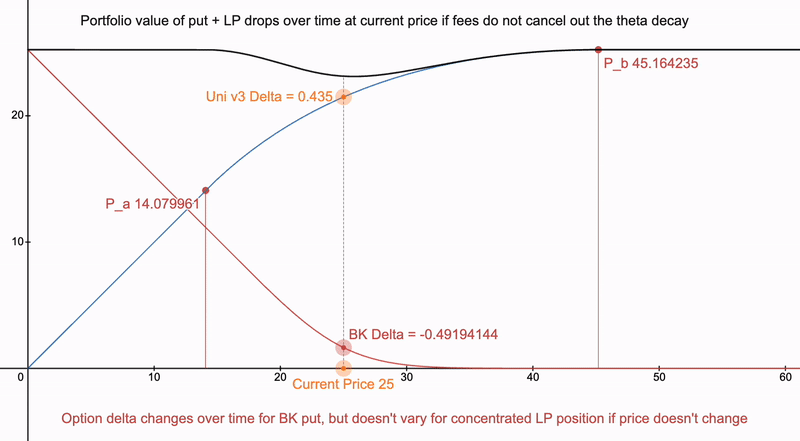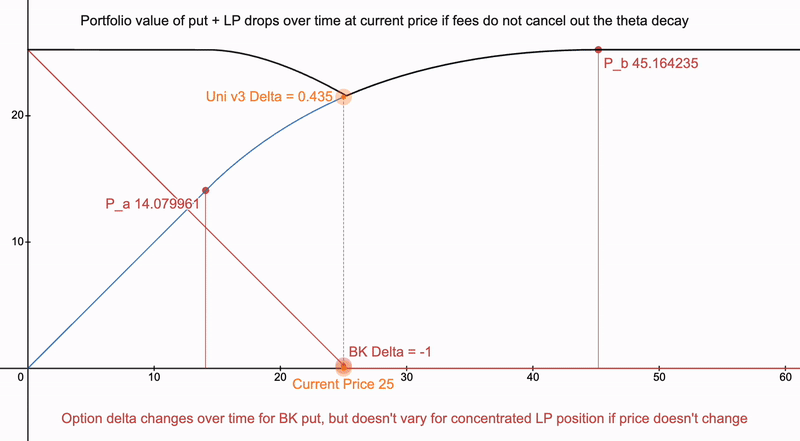
我们还需要考虑希腊字母 vega 及其如何改变这样的支付结构，因为这种情况会导致借用此类 LP 头寸的激励：

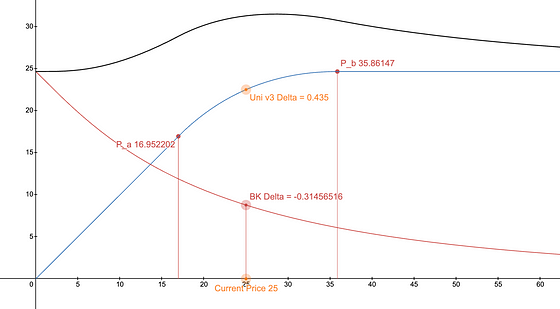一个隐含波动率过高的看跌期权可能会使对冲LP仓位变得不切实际。

以下的 Desmos 文件主要归功于 Guillaume Lambert。我在单个 LP 仓位的基础上优化了一个 Black-Scholes 期权，以动态求解近似对冲，链接:Greeks Hedge for Uni v3

但是，我们如何完全匹配集中的 LP 仓位的希腊值呢？嗯，要么我们需要改变不变量（PrimitiveFi的方法），要么我们可以使用数值方法，通过构建一组集中的 Uniswap LP 仓位，它们的希腊值之和确实与曲线匹配。我们将在第 5 部分中介绍如何使用对数正态分布来实现这一点！

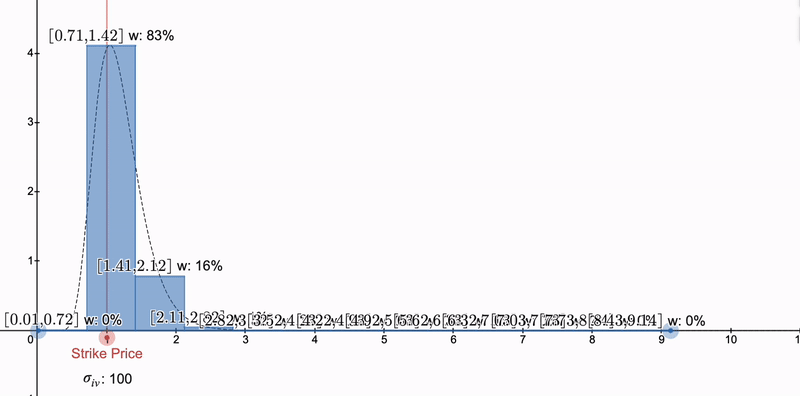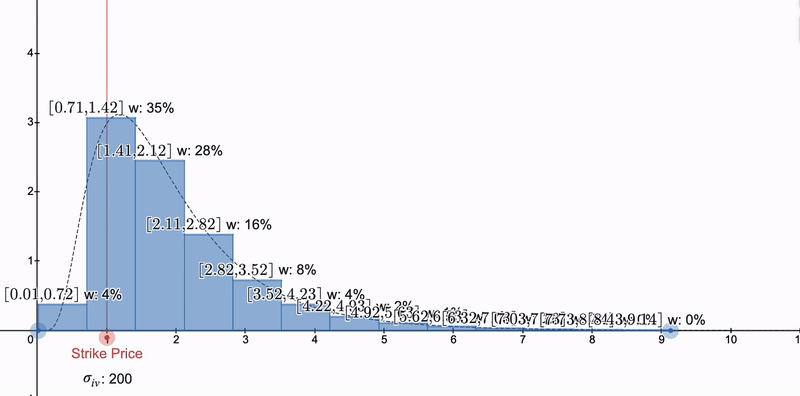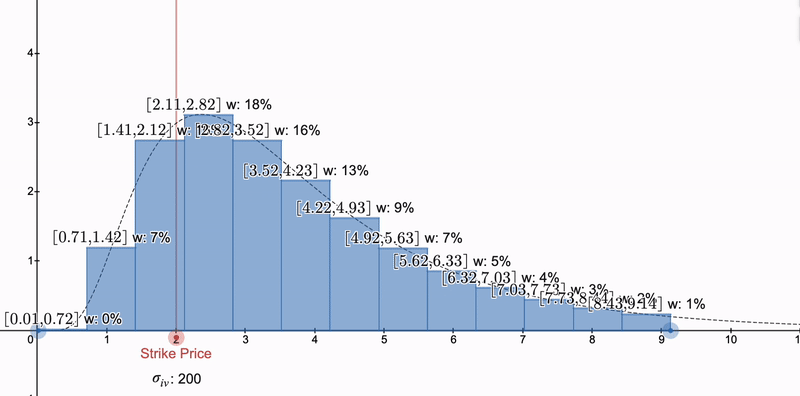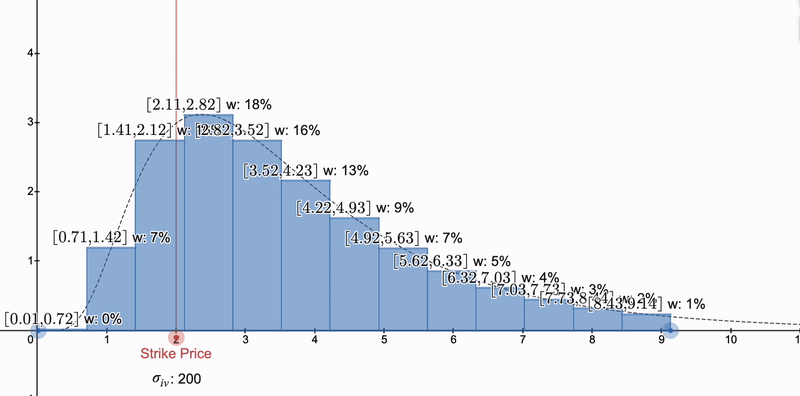
通过组合多个 LP 头寸，我们不仅可以在常规欧洲期权上，还可以在第 5 部分中的亚式期权上数值匹配希腊字母。

免责声明：请注意，为了努力弥合中英文信息差，这篇文章从Medium上翻译而来，详细的英文原文请查阅以下链接。我们也欢迎您关注我们的账号zelos-research。本研究仅供一般信息目的。Uniswap基金会很慷慨地赞助了这次私人研究的出版。它不构成投资建议或买卖任何投资的建议或招揽，并且不应用于评估做出任何投资决策的优点。不应依赖它作为会计、法律或税务建议或投资建议。本文反映了作者当前的观点。这些意见可能会随时更改而不进行更新。

原文链接：https://medium.com/@med456789d/uniswap-insights-4-of-6-lp-hedging-3b958161ab5a

关注zelos-research： https://medium.com/zelos-research
我们的github仓库： https://github.com/orgs/zelos-alpha/repositories

推荐阅读

Uniswap v3 数学洞察系列翻译 —— 第一部分 共 6 部分
Uniswap v3 数学洞察系列翻译 —— 第二部分 共 6 部分 Uniswap v3 数学洞察系列翻译 —— 第三部分 共 6 部分 Uniswap v3 数学洞察系列翻译 —— 第四部分 共 6 部分 Uniswap v3 数学洞察系列翻译 —— 第五部分 共 6 部分 Uniswap v3 数学洞察系列翻译 —— 第六部分 共 6 部分