零知识证明 - Coda SNARK挑战(Stage2)
- Star Li
- 发布于 2019-07-17 12:37
- 阅读 4387
零知识证明 - Coda SNARK挑战(Stage2)
SNARK挑战的第二阶段(Stage2)挑战的主要内容是:Groth16算法的证明生成和验证性能的优化。第二阶段的挑战又分成两部分内容:Groth16算法的证明生成(65000美金)以及Groth16算法的验证(10000美金)。
SNARK挑战使用的零知识证明算法是:BG18。BG18是Groth16算法的一种变种算法,由Zcash的团队在2018年发表。
https://eprint.iacr.org/2018/187.pdf
BG18的证明的生成,比Groth16算法增加了z变量。

BG18的验证,比Groth16算法增加了一个验证:
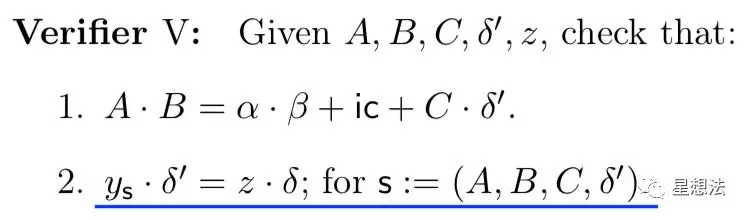01 BG18算法的验证
https://codaprotocol.github.io/snark-challenge/verifier.html
挑战的主要内容:优化JS或者WebAssembly,提高BG18算法的验证性能。这部分不需要GPU优化。不详细介绍。主要介绍一下,证明生成的挑战内容。
02 BG18算法的证明生成
https://codaprotocol.github.io/snark-challenge/problem-07-groth16-prover-challenges.html
BG18算法的证明生成逻辑涉及到以下相关的计算:
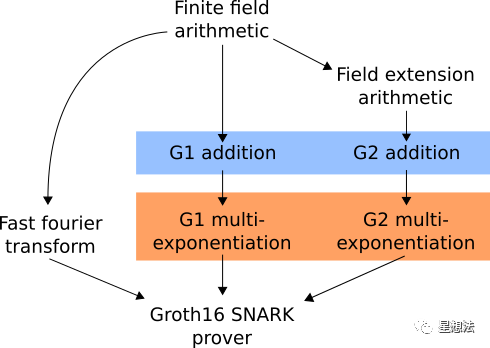
G1/G2椭圆曲线的点加和多点加法求和以及快速FFT(快速傅立叶变换)。
在$\Bbb F MNT4753$或者 $\Bbb F MNT6753$上,给定如下的参数:
-
d (uint64)
可以理解成门电路多项式的最高项的阶,也可以理解成门的个数
-
m (uint64)
m+1可以理解成整个电路向量的大小
-
A (G1, m+1)
G1椭圆曲线上m+1个点
-
B1(G1,m+1)
G1椭圆曲线上m+1个点
-
B2(G2,m+1)
G2椭圆曲线上m+1个点
-
L(G1,m+1)
G1椭圆曲线上m+1个点,可以理解成witness的部分
-
T(G1,d)
G1椭圆曲线上d个点
在挑战描述的符号下,BG18算法满足的QAP表示为:$\sum^m_{i=0}\omegaA_i(x)\sum^m_{i=0}\omegai*B(x)-\sum^m{i=0}\omega_iL(x)=H(x)T(x)$。如果电路给定,$A_i(x),B_i(x),L_i(x)$也就确定。注意$A_i(x),B_i(x),L_i(x)$是多项式,A/B1/B2/L是椭圆曲线上的点。对一个确定x,再给定G1/G2椭圆曲线的基点,对应椭圆曲线上的点也可以确定,这也是为什么直接给出A/B1/B2/L的原因(在证明生成中,L只需要计算witness的部分,所以只需要提供m+1个点就足够)。因为门电路的个数是d,也就是$T(x)=(x-t_1)(x-t_2)...(x-td)$,表示成多项式 $T(x)=x^d+T{d_1}*x^{d-1}+...$。给出的T参数,就是多项式每一项的在椭圆曲线上的点。
以上的信息,可以理解成电路的相关信息。再提供以下的输入信息:
-
w(F,m+1)
statement+witness信息
-
ca,cb,cc(F,d+1)
在给定x的情况下,$Ai(x)$的值给定。并且已知w的情况下$\sum^m{i=0}\omegaAi(x),\sum^m{i=0}\omega_iB(x),\sum^m_{i=0}\omega_i*L(x)$都可知。ca,cb,cc是$\omega^0,\omega^1,...,\omega^d$对应的各个多项式的值。
-
r(F)
r满足$\sigma^{r-1}=1$,每个$\sigma$值在每个域已经给定。在给定$\sigma,\gamma$的情况下,$\omega=\sigma^{(r-1)/(d+1)}$,也就是$\omega^{d+1}=1$。
计算BG18的证明信息:A(G1),B(G2),C(G1)。计算公式如下:
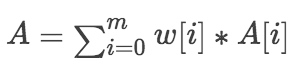


注意以上的计算公式,并不是完整的BG18或者Groth16的计算公式,但是,绝大部分的计算量已经体现。
在以上的计算中,只有$H[i]$未知。$T(x)=(x-1)(x-\omega^1)(x-\omega^2)...(x-\omega^d)=x^{d+1}-1$。
挑战的说明,给出了利用傅立叶变换和反变换的方式计算$H[i]$的过程。
-
ca,cb,cc是$\omega^0,\omega^1,...,\omega^d$对应的各个多项式的值。通过反傅立叶变换,可以获取$fA(x)=\sum^m{i=0}\omega_iA_i(x),fB(x)=\sum^m{i=0}\omega_iB_i(x),fC(x)=\sum^m{i=0}\omega_i*L_i(x)$多项式对应的系数。
-
在已知系数的情况下,并对每个系数进行偏移(每个系数乘以$\sigma^i$),通过傅立叶变换,可以计算出$\sigma ,\sigma\omega^1,\sigma\omega^2,...,\sigma\omega^d$对应的多项式的值。
-
因为
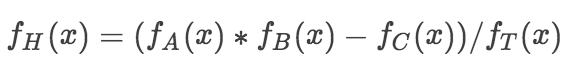
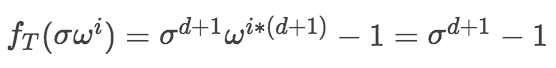 所以从第2步的结果,可以求解出$f_H(x)$的$\sigma ,\sigma\omega^1,\sigma\omega^2,...,\sigma\omega^d$对应的多项式的值。
所以从第2步的结果,可以求解出$f_H(x)$的$\sigma ,\sigma\omega^1,\sigma\omega^2,...,\sigma\omega^d$对应的多项式的值。 -
通过傅立叶逆变换,可以求的$f_H(x)$的系数的表示形式。每个系数除以$\sigma$,就能求得$f_H(x)$的系数的最终结果。
总的来说,需要三次傅立叶变换和4次傅立叶逆变换获取H多项式的系数。整个证明生成,还需要G1椭圆曲线上的4次多点加法求和计算和G2椭圆曲线上的一次多点加法求和计算。
总结:
Stage2的挑战是对BG18(Groth16)算法的性能优化。计算量涉及点加和多点加法求和以及快速FFT(快速傅立叶变换)。
- zERC20 在 Arbitrum 上线:最完备 L2 的原生隐私 45 浏览
- 零知识编年史:群 28 浏览
- 以太坊执行层优化:状态树与虚拟机 160 浏览
- 首批 ZK 漏洞利用事件已发生,但它们并非我们所预期 163 浏览
- 首次 ZK 攻击发生,且出乎意料 189 浏览
- Vitalik: 以太坊量子抵抗路线图 138 浏览
- zkMesh:2026年2月回顾 176 浏览
- 失效的 Groth16 `delta == gamma == G2 生成元` 142 浏览
- 量子可恢复的 Zcash 156 浏览
- ZK编年史:哈希登场 242 浏览
- Layer Zero 发布 Zero 链:去中心化的多核世界计算机 440 浏览
- “Jolt Inside” - 构建者需要了解的全新武器 364 浏览

