Caulk, Caulk+ 学习笔记
- Antalpha Labs
- 更新于 2024-01-24 15:17
- 阅读 1652
Caulk+ 是 Caulk 的优化版本方案，它用了一个被称为「polynomial divisibility check」的方法来替换原本的子协议，以提升 Caulk 生成证明的效率，使得证明复杂度仅与子集的大小有关，而与原向量的大小无关。
本文为 AHH Ist 期间阅读论文的学习笔记，如有笔误，欢迎指正。
Caulk 是一种向量承诺方案，可以零知识的证明一个或多个值都属于一个向量，并且不泄露这一个或者多个值的位置。Caulk 可以用来做 Membership 证明，也可以作为 Lookup Argument，并且比先前的方案在生成证明的效率上更有优势。Caulk+ 是 Caulk 的优化版本方案，它用了一个被称为「polynomial divisibility check」的方法来替换原本的子协议，以提升 Caulk 生成证明的效率，使得证明复杂度仅与子集的大小有关，而与原向量的大小无关。
1. 前提知识
1.1 Commitment Schemes
承诺方案（Commitment schemes）是一种很重要的密码学原语。它允许承诺的一方公开一个被称为承诺（commitment）的值，承诺的值与某个消息绑定（binding），同时又不泄露消息的具体内容（hiding）。
-
向量承诺（Vector Commitments）向量承诺（Vector Commitments，简称 VCs）允许通过某种方式去承诺一组有顺序的值（或者称为向量），并且在后面可以在某个特定的位置打开（open）它。
-
多项式承诺（Polynomial Commitments）多项式承诺（Polynomial Commitments）允许去承诺一个多项式，并且验证者可以用它来验证承诺多项式所声明的值的计算。可以用来验证多项式在某个点处的取值。
-
KZG10 做向量承诺KZG10 承诺方案原本是一种多项式承诺方案，它同样也可以用来做向量承诺，并证明某个值（$c_i$）等于被承诺的向量在某个特定位置（$i$）的值。假设有一个向量$\vec {c_i}$ ，长度为
N。我们可以用它生成一个多项式 $C(x)=\sum^N_i c_i \cdot \lambda_i(x)$ ，其中 $\lambdai(x)$ 是拉格朗日插值多项式，满足$C(\omega^i)=c{i\circ} {\omega^i}$ 。 是一组单位根 $\mathbb{H}={1,\omega,...,\omega^{N-1}}$ ，满足 $\omega^N =1$ 。当且仅当证明者（prover）知道向量 $\vec {c_i}$ 的所有值，才能构造多项式 $C(x)$ 。那么就可以通过对多项式 $C(x)$ 做多项式承诺并验证，来代替直接对向量 $\vec{c_i}$ 的承诺和验证。
Caulk, Caulk+（以及很多其他的 Lookup Argument ，如 Baloo，CQ，CQLin 等）就是基于 KZG10 设计的方案，所以在讨论 Caulk, Caulk+ 之前，先来看看 KZG10 方案的步骤。
1.2 KZG10 步骤
使用 KZG10 的方案来使得验证者（verifier）相信证明者（prover）知道一个多项式 C(x) 的步骤：
-
首先，证明者（prover）和验证者（verifier）获得一组安全的 SRS 参数
-
证明者（prover）使用 SRS 参数生成 C(x) 的承诺（commitment）, 并公开承诺值 $C=[c(\gamma)]_1$
-
验证者（verifier）生成随机数 $\alpha$ 并发送给证明者（prover）
-
证明者（prover）计算多项式 C(x) 在 $\alpha$ 处的取值 $y=C(\alpha)$ ，并生成证明 $\pi$ ，将 $(y,\pi)$ 发送给验证者（verifier）。$\frac{C(x)-y}{x-\alpha}=Q(x),\pi=[Q(\gamma)]_1$，
-
验证者（verifier）执行验证$e(C-[y]_1,[1]_2)=e(\pi,[\alpha]_2-[1]_2)$
KZG10 方案还可以用来一次做多点的打开（batch opening）和验证，协议步骤如下：
-
首先，证明者（prover）和验证者（verifier）获得一组安全的 SRS 参数
-
证明者（prover）使用 SRS 参数生成 C(x) 的承诺（commitment）, 并公开承诺值 $C=[c(\gamma)]_1$
-
验证者（verifier）生成一组随机挑战数 ${\alpha_1,\alpha_2,...,\alpha_m}$ 并发送给证明者（prover）
-
证明者（prover）计算多项式： a. $zI(x)=\prod^m{i=1}(x-\alpha_i)$ b. $cI=\sum^m{i=1}y_i \tau_i(x)$，其中 $y_i=c(\alpha_i),i \in [1,k],c_I(\omega^i)=y_i$ c. 证明者（prover）继续计算证明 $Q(x)=\frac{c(x)-c_I(x)}{z_I(x)},\pi=[Q(\tau)]_1$
-
证明者（prover）发送 ${\pi,{yi}^m{i=0}}$ 给验证者（verifier）
-
验证者（verifier）生成 $[C_I]_1=[c_i(\tau)]_1$ 和 $z_I(x)$，并执行验证：$e(C-[C_I]_1,[1]_2)=e(\pi,[z_I(x)]_2)$
2. Caulk 实现原理及步骤
Caulk 要实现的是在不泄露点的位置的前提下，验证向量在某个（或某些）点处的取值。这里分成在单个点验证和多个点验证两种情况来讨论。
2.1 single element
2.1.1 修改协议步骤
很显然使用最原生的 KZG10 还远不能实现 Caulk 的目标，原因是：
1）证明者（prover）在验证者（verifier）生成的一个随机点 $\alpha$ 处做验证，而 Caulk 需要在一个特定的 $\omega^i$ 点处做验证；
2）KZG10 中要求被验证的点及多项式在这个点处的取值 y 都是公开的，而 Caulk 需要隐藏这些值。
首先，KZG10 可以验证任意位置的取值，包括 $\omega^i$，当前仅当证明者（prover）知道多项式C(x)在 $\omega^i$ 处的取值，他才能算出正确的证明信息。所以我们可以验证多项式在特定点的取值。 $\frac{C(x)-y_v}{x-\omega^v}=Q(x)$
其次我们需要在上述多项的基础上继续做修改，来隐藏 $\omega^v$ 和 $y_v$ ，为了实现这个目标同时也需要隐藏等式关系中的 Q(x)。
-
$\omega^v$ 为了隐藏 $\omega^v$，这里由证明者（prover）产生了一个随机数 a，并生成多项式 $z(x)=a(x-\omega^v)=ax-b$。由于随机数 a 是不公开的，因此若证明者（prover）将 z(x) 的 commitment 发送给验证者（verifier），他无法从中提取 $\omega^v$ 的信息。但这里会引入一个问题，就是验证者（verifier）无法确信证明者（prover）发送的承诺值确实是由多项式 z(x) = ax-b 计算而来的，而不是一个作弊的值。为了解决这个问题，这里使用了一个子协议 $\pi_{unity}$ 来解决这个问题（下文中展开说明）。
-
$y_v$为了隐藏 $y_v$，这里使用了 Pedersen Commitment。Pedersen Commitment 也是一种类型的承诺方案，它允许证明者承诺某个值，而不透露它或能够改变它。（下文中展开说明）
-
Q(x)证明者（prover）产生一个随机数 s，并生成一个新的多项式$T(x)=\frac{Q(x)}{z}+hs$ 。为了保持等式成立，他需要继续生成另一个多项式 $S(x)=-\tau -sz(x)$。
现在我们可以开始构造新的等式了：
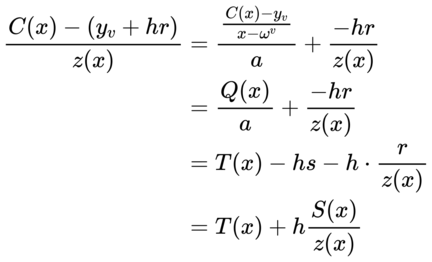
于是我们最终得到一个等式关系：
$$ C(x) - (y_v + hr) = T(x) z(x) + hS(x) $$
2.1.2 $\pi_{unity}$
对于多项式 $z(x)=a(x-\omega^v)=ax-b$ 。这里有一个重要的性质，由于 $\omega =1$，所以 $b^n=(a \cdot \omega^v)^n=a^n$ 。为了验证这层关系，我们首先定义一组值：
-
$f_0=z(1)=a-b$
-
$f_1 =z(\sigma)=a\sigma-b$
-
$f_2 =\frac{f_0-f_1}{1-\sigma}=\frac{a(1-\sigma)}{1-\sigma}=a$
-
$f_3=\sigma f_2 - f_1 = \sigma a -\sigma a + b=b$
-
$f_4 =\frac{f_2}{f_3}=\frac{a}{b}$
-
$f{5+i}=f^2{4+i} \in [0,...,logN)$
-
$f_{4+logN}=1$ 其中 $\sigma$ 是子群的单位根 $\mathbb{V}={1,...,\sigma^{n-1}}$，其中 $\sigma^n =1,n=logN+6$ 。我们再继续定义相对应的拉格朗日插值多项式 ${ \rhoi(x)}$ 和vanishing多项式$z{V_n}(X)$。现在我们继续定义一个新的多项式，使得 $f(\sigma^i)=f_i$。
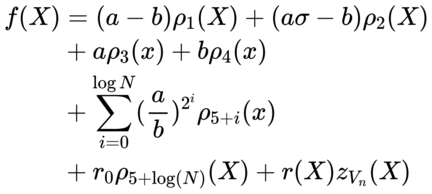
其中 $r(X)=r_1+r_2X+r_2X^2$，其中 $r_1,r_2,r_3$ 为随机数。
我们再继续构造新的多项式
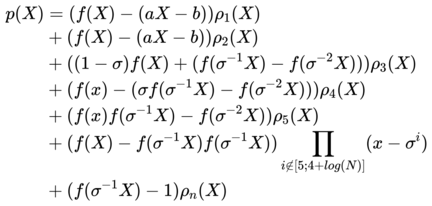
由于$x=\sigma^i,p(X)=0$ ，所以 p(X) 可以被 $z_{Vn}(X)$ 整除。所以继续定义一个多项式关系 $\hat h(X){z_{V_n}}(X)=p(X)$。因此我们可以通过验证多项式 f(X) 和 p(X) 来最终实现验证 $[z]_2$ 的目的。
完整的验证步骤：
-
证明者（prover）产生随机数 $r_0,r_1,r_2,r_3$，并生成多项式 $r(X)=r_1+r_2X+r_3X^2$
-
证明者（prover）继续定义多项式 $f(X),p(X),h(X)$ $$ \begin{aligned} f(X)&=f(\sigma^0)\rho_1(X)+f(\sigma^1)\rho_2(X) \ &+ a \rho_3(x)+b\rho4(x)\ &+ \sum^{logN}{i=0} (\frac{a}{b})^{2^i} \rho_{5+i}(x)\ &+r0 \rho{5+log(N)}(X)+r(X){z{V_n}}(X) \end{aligned} $$
$$ \begin{aligned} p(X)&=(f(X)-(aX-b))(\rho_1(X)+\rho_2(X)) \ &+((1-\sigma)f(X)+f(\sigma^{-1}X)-f(\sigma^{-2}X))\rho_3(X)\ &+(f(x)-(\sigma f(\sigma^{-1}X)-f(\sigma^{-2}X)))\rho_4(X)\ &+(f(x)f(\sigma^{-1}X)-f(\sigma^{-2}X))\rho5(X)\ &+(f(X)-f(\sigma^{-1}X)f(\sigma^{-1}X))\prod{i\notin[5;4+log(N)]}(x-\sigma^i)\ &+(f(\sigma^{-1}X)-1)\rho_n(X) \end{aligned} $$
$$ h(X)=\frac{p(X)}{z_{V_n}(X)}+x^{d-1}z(X) $$
-
证明者（prover）生成承诺 $[F]_1=[f(x)]_1$，$[H]_1=[h(x)]_1$并将其发送给验证者（verifier）
-
验证者（verifier）产生随机值 $\alpha$，并发送给证明者（prover）
-
证明者（prover）继续定义 $\alpha_1=\sigma^{-1}\alpha$，$\alpha_2=\sigma^{-2}\alpha$,
-
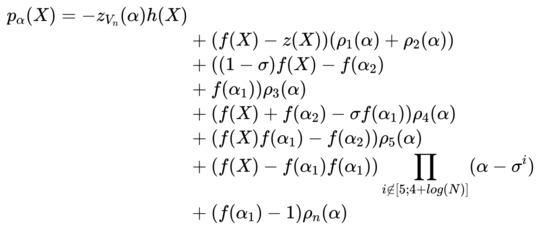
证明者（prover）生成多项式 f(x) 承诺在 $\alpha_1,\alpha_2$ 处的open的证明 $((v_1,v_2),\pi1)$，再继续生成多项式$p{\alpha}(X)$ 在 $\alpha$ 处的 open 的证明$(0,\pi_2)$ ，并将证明发送给 $(v_1,v_2,\pi_1,\pi_2)$ 验证者（verifier）
-
验证者（verifier）计算
-
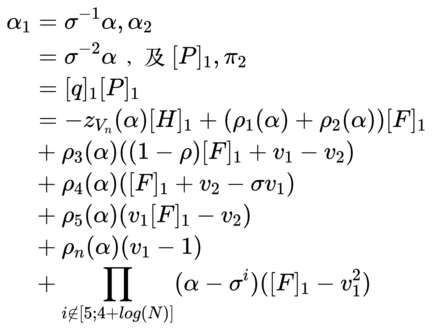
验证者（verifier）执行验证步骤 a.多项式 f(X) 在两个点 $\alpha_1,\alpha_2$ 处打开的验证：ZG.verify($[F]_1,(\alpha_1,\alpha_2),(v_1,v_2),\pi1$) b.多项式 $p{\alpha}(X)$ 的验证：
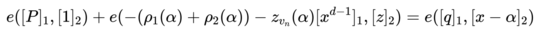
2.1.3 $\pi_{ped}$
为了隐藏 $y_c$，这里使用了 pedersen commitment，具体步骤如下：
-
在 Trusted Setup 阶段，产生一个承诺值$H=[h]_1$ ,h 是一个隐藏的随机值，任何人都不知道它的具体值
-
证明者（prover）生成两个随机数：$s_1,s_2$，产生一个承诺$R=[s_1+hs_2]$ ，并将 R 发送给验证者（verifier）
-
验证者（verifier）生成两个随机数：r，v，并发送给证明者（prover）
-
证明者（prover）产生 $y_c$ 的承诺 $cm=[y_v+h_r]$，并计算两个值 $t_1=s_1+y_vc,t2=s_2+rc$，然后将两个值发送给验证者（verifier）
-
验证者（verifier）检查等式关系 $R+c \cdot cm =[t_1+ht_2]$.
2.1.4 验证步骤
完整的验证步骤总结如下：
-
首先，证明者（prover）和验证者（verifier）获得一组安全的 srs 参数
-
证明者（prover）使用 SRS 参数生成 C(x) 的承诺（commitment）, 并公开承诺值 $C=[c(\tau)]_1$
-
证明者（prover）选择一个位置 i 的值 $y_v$
-
证明者（prover）产生两个随机值 a，s
-
验证者（verifier）生成两个随机数 r，v，并将它们发送给证明者（prover）
-
证明者（prover）产生 $y_v$ 的承诺 $cm=[y_v+hr]$， 并公开
-
证明者（prover）定义三个多项式
a.$z(X)=a(X-\omega^i)$ b.$T(x)=\frac{C(x)-v}{z(X)}+sh$ c.$S(X)=-r-sz(X)$
-
证明者（prover）生成证明 $([z]_2,[T]_1,[S]2,\pi{ped},\pi_{unity})$，并将其发送给验证者（verifier）
-
验证者（verifier）执行验证 a. $e(C-cm,[1]_2)=e([T]_1,[z]_2)+e([h]_1,[S]2)$ b. Verify($\pi{ped}$) c. Verify($\pi_{unity}$)
2.2 subset elements
上一节我们讨论了如何使用 KZG10 方案在不揭露具体值和值所在位置的前提下验证向量中某个具体值的方案。本节我们继续验证向量中多个点（m 个，点的集合定义为$I$ ）的情况。这种对 subset elements 的验证也可以被称为 KZG 向量承诺方案的position-hiding linkability。
2.2.1 修改协议步骤
这里使用 KZG10 的 batch opening 方案，与单点验证一样，同样需要做一些修改来隐藏信息。
-
$c_I(x)$
-
$z_I(x)$
-
$Q(x)$
2.2.1.1 $z_I(x)$
首先，证明者（prover）产生一个随机值$r_1$ ，并生成 $z_I(x)=r1\prod^m{i=1}(x-\omega^{k_i})$。为了验证者$z_I(x)$ ，需要通过以下方法执行验证：
-
首先，构造一个子群，单位根为$v$ ，$\mathbb{V}m={v^0,v^1,...,v^{m-1}}$, 其中 $v^m=1$。相对应的 vanishing 多项式定义为 $z{V_m}(x)$
-
然后证明者（prover）构造一个新的多项式$u(x)=\sum^{m-1}_{i=0}\omega^{k_i}\mu_i(x)$，其中 ${\mu_i(x)}$ 是拉格朗日插值多项式，使得$u(v^i)=\omega^{k_i}$
-
因为当 $x=\omega^{k_i}$ 时，$z_I(x)=0$，所以当 $x=v^i$ 时，$z_I(u(x))=0$。换句话说，$zI(u(x))$ 可以被 $z{V_m}(x)$ 整除。这里满足一个等式关系 $zI(u(x))=z{V_m}(x)H_2(x)$
-
那么也就是说我们这里的验证分为两个部分： a. $u(v^i)=\omega^{ki}$，这里使用了一个子协议 $\pi{unity}$ 来解决这个问题（下文中展开说明）。 b. $zI(u(x))=z{V_m}(x)H_2(x)$
2.2.1.2 $c_I(x)$
为了隐藏 ${y_i}$，我们要去构造一个新的多项式$cI(x)=\sum^m{i=1}y_i\tau_i(x)+(r_2+r_3X+r_4X^2)z_I(x)$证明者（prover）生成承诺 $[C_I]_1=[c_I(x)]_1$。为了验证这个承诺，需要执行以下步骤：
-
证明者（prover）产生随机数 $a{m+1}$，并构造另一个多项式 $\phi(x)=\sum^m{i=1}y_i\mui(x)+a{m+1}z_{Vm}(x)$ ，其中 $a{m+1}$ 是由证明者（prover）生成的随机值，并计算承诺 $cm=[\phi(x)]_1$。
-
由于$c_I(\omega^{k_i})=y_i$ ，所以 $c_I(u(v^i))=y_i$。也就是说对于 $i\in [0...m-1]$ ,$c_I(u(x))=\phi(x)$ 。换句话说 $cI(u(x))-\phi(x)$ 可以被 $z{V_m}(x)$ 整除。我们可以定义一个等式关系 $cI(u(x))-\phi(x)=z{V_m}(x)H_3(x)$
2.2.1.3 $Q(x)$
现在，我们重新构造等式
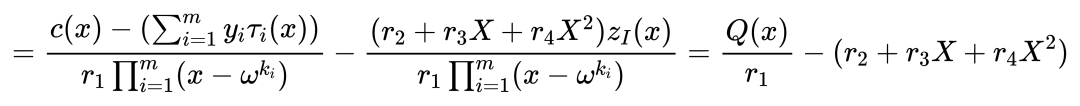
因而我们再继续定义一个新的多项式 $H_1(x)=\frac{Q(x)}{r_1}-(r_2+r_3X+r_4X^2)$.
2.2.2 $\pi_{unity}$
具体步骤如下：
-
证明者（prover）生成一组随机数$t_1,...,t_m$
-
证明者（prover）生成多项式$us(X)=\sum^m{j=1}(\omega^{i_j})^{2^s}u_j(X)+tsz{V_m}(X),s={1,...,m}$
-
证明者（prover）继续定义多项式:
-
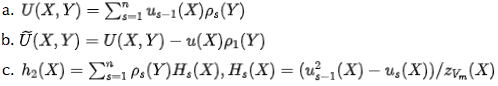
证明者（prover）计算承诺 $[\tilde{U}]_1=[\tilde{U}(x^n,x)]_1,[h_2]_1=[h_2(x^n,x)]_1$，并发送给验证者（verifier）
-
验证者（verifier）产生随机数 $\alpha$，并发送给证明者（prover）
-
证明者（prover）定义多项式 $h1(Y)=(U^2(\alpha,Y)-\sum^n{s=1}u^2_{s-1}(\alpha)\rhos(Y))/z{V_n}(Y)$，并计算承诺$[h_1]_1=[h_1(x)]_1$ ，并发送给验证者（verifier）
-
验证者（verifier）生成随机数$\beta$ ，并发送给证明者（prover）
-
证明者（prover）继续计算多项式 P(Y)，及多项式 $u(X)m,\widetilde{U}(X,Y),h_2(X,Y),\widetilde{U}(\alpha,Y),p(Y)$ 的证明
- $P(Y)=(U^2(\alpha,\beta)-h1(Y)z{V_m}(\beta)-\widetilde{U}(\alpha,\beta \sigma)+id(\alpha)\rhon(\beta))-z{V_m}(\alpha)h_2(\alpha,Y)$
- $(v_1,\pi_1)=KZG.Open(srs,u(x),X=\alpha)$
- $([\widetilde{U}(\alpha,x)]_1,\pi_2)=KZG.Open(srs,\widetilde{U}(X,Y),X=\alpha)$
- $([\widetilde{h}_2(\alpha,x)]_1,\pi_3)=KZG.Open(srs,\widetilde{h_2}(X,Y),X=\alpha)$
- $((0,v_2,v_3),\pi_4)=KZG.Open(srs,\widetilde{U}(\alpha,Y),X=(1,\beta,\beta \sigma))$
- $(0,\pi_5)=KZG.Open(srs,p(Y),Y=\beta)$
-
证明者（prover）定义 $([\widetilde{U}_{\alpha}]_1=[\widetilde{U}(\alpha,x)]1),[\widetilde{h}{2,\alpha}]_1=[\widetilde{h}_2(\alpha,x)]1$，并将 $([\widetilde{U}\alpha,\widetilde{h}_{2,\alpha}]_1,v_1,v_2,v_3,\pi_1,,\pi_2,,\pi_3,\pi_4,,\pi_5)$ 发送给验证者（verifier）
-
验证者（verifier）计算 a.$\begin{aligned}U=v_1\rho_1(\beta)+v_2\end{aligned}$ b.$[P]_1=U^2-[h_1]1 z{V_m}(\beta)-(v_3+id(\alpha)\rhon(\beta))-z{Vm}(\alpha)[h{2,\alpha}]_1$
-
验证者（verifier）对 $\pi_1,\pi_2,\pi_3,\pi_4,\pi_5$ 执行验证
2.2.3 验证步骤
完整的验证步骤总结如下：
-
首先，证明者（prover）和验证者（verifier）获得一组安全的 SRS 参数
-
证明者（prover）使用 SRS 参数生成 C(x) 和 $\phi(x)$ 的承诺（commitment）,并公开承诺值 $C=[c(\tau)]_1$ , $cm=[\phi(x)]_1$
-
证明者（prover）产生随机值 $\boldsymbol{r}_1,\boldsymbol{r}_2,\boldsymbol{r}_3,\boldsymbol{r}_4,\boldsymbol{r}_5,\boldsymbol{r}_6,\boldsymbol{r}_7$
-
证明者（prover）定义多项式： a. $z_I(x)=r1\prod{i=1}^m(x-\omega^{k_i})$ b.$cI(x)=\sum^m{i=1}y_i\tau_i(x)+(r_2+r_3x+r_4x^2)z_I(x)$ c.$H_1(x)=\frac{Q(x)}{r_1}-(r_2+r_3x+r4x^2)$ d.$u(x)=\sum^m{i=1} \omega^{k_i} \mu_i(x)+(r_5+r_6x+r7x^2)z{V_m}(x)$
-
证明者（prover）为 u(x) 生成证明 $\pi_{unity}$ ，并生成承诺 $[C_I]_1=[C_I(x)]_1,[z_I]1=[z_I(x)]_1,[u]_1=[u(x)]_1,[H_1]_2=[H_1(x)]2$。然后证明者（prover）发送这几个承诺和证明 $\pi{unity}$ 给验证者（verifier）
-
验证者（verifier）生成随机值 $\mathbf{x}$ ，并将其发送给证明者（prover）
-
证明者（prover）将两个多项式 $zI(u(x))=z{V_m}(X)H_2(x)$ 和 $cI(u(x))-\phi(x)=z{V_m}(x)H_3(x)$ 结合起来生成新的多项式 $z_I(u(x))+\mathbf{x}(cI(u(x))-\phi(x))=z{V_m}(x)H_2(x)$。
-
证明者（prover）计算证明 $[H_2]_1=[H_2(x)]_1$ ，并发送给验证者（verifier）
-
验证者（verifier）生成新的随机值 $\alpha $ ，并发送给证明者（prover）
-
证明者（prover）继续构造多项式 $p_1(x),p_2(x)$ a. $p_1(x)=z_I(x)+\mathbf{x}c_I(x)$ b. $p_2(x)=z_I(u(\alpha))+\mathbf{x}(cI(u(\alpha))-\phi(X))-z{V_m}(\alpha)H_2(x)$
-
证明者（prover）生成多项式 $p_1(x),p_2(x),u(x)$ 的证明，并发送给验证者（verifier）
-
验证者（verifier）计算 a. $[P_1]_1=[z_I]_1+\mathbf{x}[C_I]_1$ b. $[P_2]_1=v2-\mathbf{x}cm-z{v_m}(\alpha)[H_2]_1$
-
验证者（verifier）执行验证 a. $\pi{unity}$ ， b. KZG.Verify( $\left[u\right]{1}$ ) c. KZG.Verify( $[P_1]_1$ ) d. KZG.Verify( $\left[P_2\right]_1$ ) e. $e([C]_1-[C_I]_1,[1]_2)=e([z_I]_1,[H_1]_2)$
2.2.4 复杂度
Caulk 的证明时间相比较于之前的 Lookup Argument 协议在证明时间上有了很大的提升。当向量的大小为 N，而子向量的大小为 m 时，生成证明的时间复杂度为 $O(m\log N+m^2)$ ，验证证明的复杂度为 $O(\log(\log N))$ 。
3. Caulk+ 优化方案
Caulk+ 对 Caulk 的算法步骤做了改进，将生成证明的复杂度降低到 $O(m^2)$ ，这样证明的复杂度仅与子集的大小 m 有关，与向量 v 的长度 N 无关。
3.1 证明计算优化
KZG10 做单点验证时，检查的等式关系为： $\begin{aligned}\frac{C(x)-c_i}{x-\omega^i}&=Q_i(x)\end{aligned}$
KZG10 做多点（batch）验证时，检查的等式关系为： $\begin{aligned}\frac{c(x)-c_I(x)}{z_I(x)}=Q(x)\end{aligned}$
多点的证明( $Q(x)$ )和单点的证明 $\left(Q_i(x)\right)$ 之间存在着关系：
$\frac{c(x)-c_I(x)}{z_I(x)}=\frac{c(x)-cI(x)}{\prod{i\in I^{(x-\omega^i)}}}=\sum{i \in I} \frac{C(x)-ci}{(x-\omega^i)\prod{j \in I,i \ne j^{(\omega^i-\omega^j)}}}=\sum_{i \in I}\frac{Qi(x)}{\prod{j \in I,i \ne j^{(\omega^i-\omega^j)}}}$
因此证明者（prover）可以预先计算好所有的 ${Qi}{i\in[0..N)}$ ，这样在每次生成证明的时候，直接带入 ${Qi}{i\in[0..N)}$ 去计算 Q(x)。
3.2 协议步骤
下面是完整的协议步骤：
-
首先，证明者（prover）和验证者（verifier）获得一组安全的 SRS 参数
-
证明者（prover）构造关于向量 $\overrightarrow{c}$ 的多项式 C(x) ，并计算承诺 $C=[c(\tau)]_1$
-
证明者（prover）先计算两组承诺 a. ${[W_1^{(i)}]2}{i\in I},W_1^{(i)}(X)=(C(X)-c_i)/(C-\omega^i)$ b. ${[\boldsymbol{W}_2^{(i)}]2}{i\in I},W_2^{(i)}(X)=z_I(X)/(X=\omega^i)$
-
证明者（prover）计算 $\phi(x)$ 的承诺（commitment）,并公开承诺值 $cm=[\phi(x)]_1$
-
证明者（prover）产生随机数$\tau_1,\tau_2,\tau_3,\tau_4,\tau_5$
-
证明者（prover）计算多项式 a. $z_I(x)=r1\prod{i=1}^m(x-\omega^{k_i})$ b. $cI(x)=\sum^m{i=1} y_i \tau_i(x),c'_I(x)=c_I(x)+(r_2+r_3x+r_4z^2)zI(x)$ c. $u(x)=\sum^m{i=1}\omega^{k_i}\mu_i(x)+(r_5+r6x)z{V_m}(x)$，满足 $\color{blue}{u(v_i)=\omega^{u(i)},i\in[m]}$
-
证明者（prover）计算承诺 $[C_I]_1=[C_I(x)]_1,[z_I]_1=[z_I(x)]_1,[u]_1=[u(x)]_1,[H_1]_2=[H_1(x)]_2$。并发送给验证者（verifier）
-
验证者（verifier）产生随机数 $\chi_1,\chi_2$ ，并发送给证明者（prover）
-
证明者（prover）计算 a. 将两个多项式 $zI(u(x))=z{V_m}(X)H_2(x)$ 和 $cI(u(x))-\phi(x)=z{V_m}(x)H_3(x)$ 结合起来生成新的多项式 $z_I(u(x))+\chi_1(cI(u(x))-\phi(x))=z{V_m}(x)H_2(x)$。 b. $[W_1(X)+\chi_2W_2(X)]2 = \sum{i \in I} \frac{[W_1^{(i)}(x)]_2+ \chi_2[W_2^{(i)}(x)]2}{\prod{j \in I,i\ne j^{\omega^i-\omega^j}}}$
-
证明者（prover）计算承诺，并发送给验证者（verifier） a. $[W]_2=r_1^{-1}[W_1(X)+ \chi_2W_2(X)]_2-[r_2+r_3x+r_4x^2]_2$ b. $[H_2]_1=[H_2(x)]_1$
-
验证者（verifier）产生随机数 $\alpha $ ，并发送给证明者（prover）
-
证明者（prover）继续构造多项式 $p_1(x),p_2(x)$ a. $p_1(x)=z_I(x)+\chi_1c_I(x)$ b. $p_2(x)=z_I(u(\alpha))+\chi_1(cI(u(\alpha))-\phi(X))-z{V_m}(\alpha)H_2(x)$
-
证明者（prover）生成多项式 $p_1(x),p_2(x),u(x)$ 的证明，并发送给验证者（verifier）
-
验证者（verifier）首先计算： a. $[P_1]_1=[z_I]_1+\chi_1[C_I]_1$ b. $[P_2]_1=v_2-\chi1cm-z{v_m}(\alpha)[H_2]_1$
-
验证者（verifier）执行验证： a. KZG.Verify( $u,\alpha,v_1,\pi_1$ ) b. KZG.Verify( $p_1,v_1,v_2,\pi_2$ ) c. KZG.Verify( $p_2,\alpha,0,\pi_3$ ) d. $e([C]_1-[C_I]_1+\chi_2[x^n-1]_1,[1]_2)=e([z_I]_1,[W]_2)$
3.3 单点验证的协议改进
上一小节中，我们讨论的协议步骤，原来的子协议被一种优化过的新方案所代替，而对于单点验证的步骤中，若采用同样的优化，可能引入一个问题，就是无法保证 $\left[z\right]_2$ 确实是由正确的 z(x) 多项式计算得来的。为了解决这个问题，这里可以用 schnor 协议来执行验证。
3.3.1 schnorr protocol 相关部分的步骤
-
证明者（prover）生成随机数 $k,\hat{v},\hat{r},\hat{k}$
-
证明者（prover）生成多项式 $A(x)=y_v+k(x-1)$ ,并生成承诺 $A=[A(x)]_1$
-
证明者（prover）生成 $V'=[\hat{v}+\hat{r}h]_1$ , $A'=[\hat{v}+\hat{k}(x-1)]_1$ ，并将 A, A', V' 发送给验证者（verifier）
-
验证者（verifier）生成随机值 $\chi$
-
证明者（prover）生成三个值，并发送给验证者（verifier） a. $s_v=\hat{v}+\chi v$ b. $s_r=\hat{r}+\chi r$ c. $s_k=\hat{k}+\chi k$
-
验证者（verifier）执行验证 a. $[s_v]_1+s_r[h]_1=V'+\chi cm$ b. $[s_v]_1+s_k[x_1]_1=A'+\chi A$
