简析 Cached Quotients Lookup Arguments
- Antalpha Labs
- 发布于 2024-01-29 17:57
- 阅读 3824
Lookup Arguments 允许证明者(prover)证明一个值属于一个预先定义的集合。
本文来自于 PSE Acceleration Program[^1ID1]的赞助支持。
代码: pylookup[^2ID2]
这个代码是参考 CQ 的 paper 实现的,请看
README.md了解如何运行。另外,其中还包括了一个cq.ipynb文件, 是一个 Python notebook 版本的实现,是一个简化版本的 CQ 实现,和这个教程比较接近。
Lookup 要解决的问题
在零知识证明系统中,通常会利用算数化过程将一个计算问题转化为与之等价的数学表达形式(通常是多项式),这样就可以利用数学性质来对多项式进行变换,计算和验证。这是构建零知识证明的关键步骤,因为它使得复杂的计算过程可以在数学上被精确地表达和验证。
但有些计算不能被很好的算数化,或者算数化后会产生更多的约束(多项式)。比如证明一个值是否在一个范围内( $0<x<5$ ),可能需要 10 个以上的约束。这时候使用 Lookup Arguments 能减少约束的数量,减少生成的证明大小。
Lookup Arguments 允许证明者(prover)证明一个值属于一个预先定义的集合。
拿刚才的例子来说,证明 $0<x<5$ 只需要一个 lookup 约束: $x \in {1, 2, 3, 4}$ , 即证明 $x$ 在表 ${1, 2, 3, 4}$ 中。
| Table |
|---|
| 1 |
| 2 |
| 3 |
| 4 |
| 上面的例子是一个单列的表格。更进一步,一个表可以表达任意的关系,只要对应的输入输出能在表中找到,我们就可以说 lookup 证明成立。 | Input 1 | Input 2 | Input3 | Output |
|---|---|---|---|---|
| 1 | 2 | 3 | 6 | |
| 2 | 3 | 4 | 24 | |
| 3 | 3 | 8 | 48 | |
| 4 | 8 | 3 | 13 | |
| 13 | 6 | 4 | 33 |
比如表格第一行我们可以定义为一个加法: $1+2+3=6$ ,只要给定的查找是 ${1, 2, 3, 6}$ ,就满足 lookup 的约束; 第二行可以定义为乘法: $2 3 4 = 24$ ,只要给定的查找是 ${2, 3, 4, 24}$ ,就满足 lookup 的约束。
CQ 的贡献
从论文中的对比(下图)可以看到,CQ(Cached Quotients Lookup Arguments) 是目前 prover 计算复杂度最低的 lookup argument,仅为 $O(n logn)$ ,这一点通过一定的预处理来实现。和 Baloo 相比,CQ 有更少的群运算和更小的 proof size。
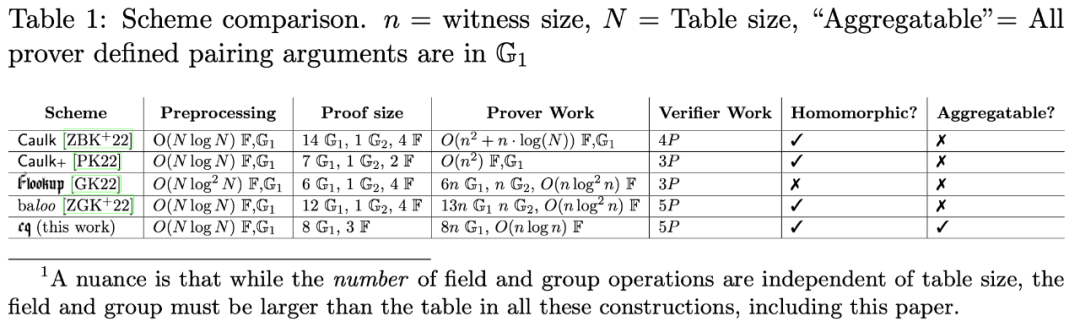
CQ 和上表中提到的四个 lookup arguments 主要差别是,CQ 利用了对数导数这个技巧,让 prover 的计算可以基于原始的大表,而不需要从大表中提取出一个子表(subtable),从而让 prover 的计算更加高效。
下面我们针对 CQ 的核心原理进行解释,如果你对更多的细节和优化感兴趣,可以参考原始的 paper。
对数导数
lookup argument 就是要证明向量/表 $\vec f$ 中的元素都在 $\vec t$ 中,这一点和其它 lookup argument 都是一致的。
假设:
-
$\vec f = {f_1, f_2, f_3, f_4, ..., f_n}$
-
$\vec t = {t_1, t_2, t_3, t_4, .., t_n}$
例如:
-
$\vec f = {1, 2, 2, 3, 3, 3}$
-
$\vec t = {1, 2, 3, 4}$
上面的问题可以转化为一个新的问题: 用这些元素构建一个多项式, 他们拥有相同的根:
-
$f(x) = (x-1)(x-2)(x-2)(x-3)(x-3)(x-3)$
-
$t(x) = (x-1)^1(x-2)^2(x-3)^3(x-4)^0$
这样的好处是,我们可以利用多项式的数学性质进行后续的计算和证明。
注意 $t(x)$ 中需要统计 $\vec f$ 中出现重复元素的次数,作为多项式 $t(x)$ 对应根的位置的幂次,没有出现的元素的次数为 0。可以看到, $\vec f$ 中元素在 $\vec t$ 中出现的次数:
-
1 在 $\vec t$ 中出现的次数为 1
-
2 出现次数为 2
-
3 出现次数为 3
-
4 出现次数为 0
这里可以用一个向量 $\vec m$ 表示:
$\vec m = {1, 2, 3, 0}$
所以 $t(x)$ 有这样的构造: $t(x) = (x-1)^1(x-2)^2(x-3)^3(x-4)^0$ 。
可以看到,如果 $f(x)$ 等于 $t(x)$ ,就可以说 $\vec f$ 中的元素都在 $\vec t$ 中,满足 lookup argument 的证明。
构造连乘的多项式还有一个好处,可以不用考虑 $\vec f$ 和 $\vec t$ 两个向量中元素的顺序。
不过实际中通常不会直接对比,因为:
-
$\vec f$ 通常是秘密的值,不是公开的,不能直接对比
-
$\vec f$ 和 $\vec t$ 的 size 一般都非常大,构建的多项式次数很高,相对难以处理
有没有更好的方式证明 $f(x) = t(x)$ 呢?
有。CQ 使用了Multivariate lookups based on logarithmic derivatives[^3ID3]论文中提到的「对数导数法」,将乘法关系转换为加法关系,让证明变得简洁了很多。
什么叫对数导数法?
在数学中,对数导数法是一种求函数导数的技巧,特别适用于复杂函数的求导,尤其是当函数是多个函数的乘积形式时。这种方法通过应用自然对数( $ln$ )和链式法则来简化求导过程。
下面我们来计算 $f(x) = (x-1)(x-2)^2(x-3)^3$ 的对数导数。按照对数导数法的步骤,我们先对 $f(x)$ 取对数,然后对所得表达式求导。下面是具体的计算步骤:
取对数:
$$ \begin{array}{c} \ln(f(x)) &= \ln((x-1)(x-2)(x-2)\ &(x-3)(x-3)(x-3)) \end{array} $$
展开对数(利用对数的性质,将乘积转换为求和):
$$ \begin{array}{c} \ln(f(x)) & = \ln(x-1) + \ln(x-2) \ &+ ln(x-2)+ \ln(x-3)\ &+ {} ln(x-3) + \ln(x-3) \end{array} $$
对等式两边求导(应用链式法则和基本导数规则):
$$ \begin{array}{c} \frac{d}{dx}\ln(f(x)) &= \frac{d}{dx}(\ln(x-1) + \ln(x-2)\ &+ \ln(x-2)+ \ln(x-3)\ &+ \ln(x-3) + \ln(x-3)) \end{array} $$
化简为:
$$ \begin{array}{c} \frac{f'(x)}{f(x)} &= \frac{1}{x-1} + \frac{1}{x-2}+ \frac{1}{x-2} \ &+ \frac{1}{x-3} + \frac{1}{x-3} + \frac{1}{x-3} \end{array} $$
即:
$$
\frac{f'(x)}{f(x)} = \sum_{j \in |\vec f|} \frac{1}{x-f_j}
$$
同样对 $t(x)$ 求对数导数得到:
$$
\frac{t'(x)}{t(x)} = \frac{1}{x-1} + \frac{2}{x-2}+ \frac{3}{x-3}
$$
即:
$$
\frac{t'(x)}{t(x)} = \sum_{i \in |\vec t|} \frac{m_i}{x-t_j}
$$
所以需要证明:
$$
\frac{f'(x)}{f(x)} = \frac{t'(x)}{t(x)}
$$
即:
$$
\sum_{j \in |\vec f|} \frac{1}{x-fj} = \sum{i \in |\vec t|} \frac{m_i}{x-t_i}
$$
简化一下写法,定义 $a_i = m_i / (x - t_i)$ 和 $b_j = 1 / (x - f_j)$ ,
即需要证明:
$$
\sum_i a_i = \sum_j b_j
$$
可以看到这个过程将多个函数的乘积转换为求和的形式。最终将 lookup 证明转换为证明对数导数( $\frac{f'(x)}{f(x)}$ 和 $\frac{t'(x)}{t(x)}$ ) 相等。
对数导数 lookup 协议
通过上面的对数导数可以构建一个简单的 lookup argument:
-
prover 给 verifier 发送 $\vec f, \vec t, \vec m$
-
verifier 给 prover 发送随机数 $\beta$
-
prover 给 verifier 发送多个值: $a_i = m_i / (\beta - t_i)$ 和 $b_j = 1 / (\beta - f_j)$ ,其中 $i$ 和 $j$ 的取值范围为 $\vec t$ 和 $\vec f$ 中元素的个数,即 $i \in |\vec t|,j \in |\vec f|$
-
verifier 做三种检查
- $a_i$ 值检查: $a_i * (\beta - t_i) = m_i$
- $b_i$ 值检查: $b_i * (\beta - f_i) = 1$
- sum 检查: $\sum_i a_i = \sum_j b_j$
对于 $a_i$ 和 $b_i$ 的检查,上面的 lookup 协议有一个问题,就是 proof size 比较大,因为需要将所有的 $a_i$ 和 $b_i$ 值都发给 verifier。要解决这个问题,我们可以利用 Schwartz-Zippel 定理,将所有 $a_i$ 和 $b_i$ 的值编码到多项式中,然后 verifier 只需要发送一个随机值进行验证就可以保证 prover 提供的所有 $a_i$ 和 $b_i$ 的值是正确的。
对于 sum 检查,我们可以直接使用 univariate sumcheck。
下面我们分别看看如何构造对应的证明。
多项式构造和 pairing: 证明 $a_i$ 和 $b_i$
为了验证:
-
$a_i$ 的正确性: $a_i * (\beta - t_i) = m_i$
-
$b_i$ 的正确性: $b_i * (\beta - f_i) = 1$
我们通过将 $a_i$ 和 $b_i$ 分别构造成一个多项式,然后利用多项式的性质来进行验证。
所以需要:
-
从 $a_i$ 构建出多项式 $A(x)$ ,并验证构造的正确性
-
从 $b_i$ 构建出多项式 $B(x)$ ,并验证构造的正确性
构造多项式我们通常使用拉格朗日插值法。这就需要构造一系列 ${x_i, y_i}$ 值对,将这些值对插值成多项式,通常 ${x_i}$ 的值来自于一个乘法子群,群的大小为 ${y_i}$ 的大小,这里分别为 $|\vec t|$ 和 $|\vec f|$
如何构造 $A(x)$ ?
-
verifier 发送随机数 $\beta$ ,令 $x = \beta$
-
选择大小为 $|\vec t|$ 的乘法子群 $H_t = {\omega_i}$ , $i \in |\vec t|$
-
$A(\omega_i) = a_i = m_i / (t_i - \beta)$ 。 ${x_i, y_i}$ 值对为 ${\omega_i, a_i}$
-
使用拉格朗日插值法得到多项式 $A(x)$
如何检查 $A(x)$ 被正确构造?
-
分别对 $\vec m$ 和 $\vec t$ 在乘法子群上进行插值得到多项式 $M(x),T(x)$
-
在乘法子群 $H_t$ 上,多项式满足 $A(x) = M(x)/(T(x) - \beta)$
-
变换为 $A(x)(T(x) - \beta) - M(x) = 0$
-
由多项式余式定理得到 $A(x)(T(x) - \beta) - M(x) = Q_A(x) * Z_A(x)$ 。这个等式对 $x$ 为群上的任意值都成立。其中 $Q_A(x)$ 为商多项式, $Z_A(x) = \prod_i(x - \omega_i)$ 为消失多项式
-
prover 发送 a. $A(x)$ 的承诺 $[A(x)]_1$ b. $Q_A(x)$ 的承诺 $[Q_A(x)]_1$ c. $M(x)$ 的承诺 $[M(x)]_1$
-
verifier 自行计算 $T(x)$ 的承诺 $[T(x)]_2$ 和 $Z_A(x)$ 的承诺 $[Z_A(x)]_2$ ,然后通过椭圆曲线的 pairing 进行 KZG 验证: $e([T(x)]_2, [A(x)]_1) = e([1]_2, [A(x)]_1 \beta + [M(x)]_1) e([Z_A(x)]_2, [Q_A(x)]_1)$
注意: 和 paper 有些区别的地方是,为了方便解释,文章中有些地方使用了 $-$ 号而不是 $+$ 号,这是因为在群上做减法运算会转化成加法运算,比如对于 $modulus = 5$ 的群, $\beta=-2\%5 = 3$ ,所以 $(x - 2)\%5 = x + 3$ ,我们随时可以将减法转化为加法表示,因此在符号表示上,在有些场景下不做区分。
同样的方法构造 $B(x)$ :
-
verifier 发送随机数 $\beta$ ,令 $x = \beta$
-
选择大小为 $|\vec f|$ 的乘法子群 $H_f = {\omega_j}$ , $j \in |\vec f|$
-
$B(\omega_j) = b_j = 1 / (f_j - \beta)$ , ${x_j, y_j}$ 值对为 ${\omega_j, b_j}$
-
使用拉格朗日插值法得到多项式 $B(x)$
检查 $B(x)$ 被正确构造:
-
对 $\vec f$ 在乘法子群上进行插值得到多项式 $F(x)$
-
在乘法子群 $H_f$ 上,多项式满足 $B(x) = 1/(F(x) - \beta)$
-
变换为 $B(x)(F(x) - \beta) - 1 = 0$
-
由多项式余式定理得到 $B(x)(F(x) - \beta) - 1 = Q_B(x) * Z_B(x)$ 。这个等式对 $x$ 为群上的任意值都成立. 其中 $Q_B(x)$ 为商多项式, $Z_B(x) = \prod_j(x - \omega_j)$ 为消失多项式
-
prover 发送 a. $B(x)$ 的承诺 $[B(x)]_1$ b. $Q_B(x)$ 的承诺 $[Q_B(x)]_1$ c. $F(x)$ 的承诺 $[F(x)]_1$
-
verifier 自行计算 $Z_B(x)$ 的承诺 $[Z_B(x)]_2$ ,然后通过椭圆曲线的 pairing 进行验证: $e([F(x)]_2, [B(x)]_1) = e([1]_2, [B(x)]_1 \beta + [1]_1) e([Z_B(x)]_2, [Q_B(x)]_1)$
注意: paper 中的验证对计算过程进行了一定的优化,我们这里为了叙述方便,没有使用和 paper 中一样的验证方式,不过核心原理是一样的, 都是通过 pairing 进行 KZG 验证。
Sumcheck
接下来我们要验证 sum 成立: $\sum_i a_i = \sum_j b_j$
前面证明了左右两边每一项都是正确的,那下面需要证明左右两边的加和是正确的,也就是需要彼此相等. 证明的方法是 sumcheck。可以利用这样一个引理来证明:
$$ \sum_{a \in H} f(a) = t \cdot f(0) $$
其中:
-
$H$ 为乘法子群: $H={1, \omega, \omega^2, ..., \omega^{t-2}, \omega^{t-1} }$ , $t$ 是 $H$ 中元素的个数, $t=|H|$ , $\omega$ 是单位根
-
$f(x)$ 为一个多项式, $$ \begin{array}{c}f(x) &= f_0 + f_1x + f2x^2 + ...\ &+ f{t-2}x^{t-2} + f_{t-1}x^{t-1} \end{array} $$
让我们来分解一下计算过程,将 $a$ 取 $H$ 中的值带入 $f(x)$ 可得:
$$ \begin{align} & \sum_{a \in H} f(a) = f(1) + f(\omega) + f(\omega^2) + ... + + f(\omega^t-1) \ & \ & \ & = f_0 + f_1 + f2 + ... + f{t-2} + f_{t-1} \ & + f_0 + f_1\omega + f2\omega^2 + ... + f{t-2}\omega^{t-2} + f_{t-1}\omega^{t-1} \ & + f_0 + f_1(\omega^2) + f2(\omega^2)^2 + ... + f{t-2}(\omega^2)^{t-2} + f_{t-1}(\omega^2)^{t-1} \ & . \ & . \ & . \ & + f_0 + f_1(\omega^{t-2}) + f2(\omega^{t-2})^2 + ... + f{t-2}(\omega^{t-2})^{t-2} + f_{t-1}(\omega^{t-2})^{t-1} \ & + f_0 + f_1(\omega^{t-1}) + f2(\omega^{t-1})^2 + ... + f{t-2}(\omega^{t-1})^{t-2} + f_{t-1}(\omega^{t-1})^{t-1} \ & \ & \ & = t \cdot f_0 + f1\sum{i \in t}(\omega)^i + f2\sum{i \in t}(\omega^2)^i + ... + f{t-2}\sum{i \in t}(\omega^{t-2})^i + f{t-1}\sum{i \in t}(\omega^{t-1})^i \ \end{align} $$
上面公式中,除了第一项,后面的 $t-1$ 项每个 $sum$ 都为 0。这是因为,每个 $\omega^i$ 都是有限域上乘法子群中的元素,而乘法子群中每个元素都可以作为乘法子群的生成元,也就说明后面的 $t-1$ 项的每个 $sum$ 都是乘法子群中所有元素的 $sum$ 。
有限域上的乘法子群与复数域上的单位圆结构类似。在单位圆上:
-
所有元素都由单位元生成并均匀分布在单位圆上
-
每个元素基于原点都有另外一个对称的点, 这两点复平面上的矢量和抵消,加和等于 0
因此所有单位圆的元素 $sum$ 等于 0。
因为要使用 FFT(Fast Fourier Transform)做多项式的插值,所以要求乘法子群的元素个数是 2 的幂次个。在乘法子群中,每个元素也有对称的点,对于拥有 $t$ 个元素的乘法子群 $H$ : $Hi + H{i+t/2} = 0$ ,这两个对称的点相加等于 0,所以乘法子群所有元素的 $sum$ 也等于 0。这就是为什么后面的 $t-1$ 项每个 $sum$ 都为 0:
$$ \begin{align} & \sum{i \in t}(\omega)^i = 0\ & \sum{i \in t}(\omega^2)^i = 0 \ & . \ & . \ & . \ & \sum{i \in t}(\omega^{t-2})^i = 0 \ & \sum{i \in t}(\omega^{t-1})^i = 0 \ \end{align} $$
所以:
$$ \begin{align} & \sum_{a \in H} f(a) \ & = t \cdot f_0 + f1\sum{i \in t}(\omega)^i + f2\sum{i \in t}(\omega^2)^i + ... + f{t-2}\sum{i \in t}(\omega^{t-2})^i + f{t-1}\sum{i \in t}(\omega^{t-1})^i \ & = t \cdot f_0 + f_1 \cdot 0 + f2 \cdot 0 + ... + f{t-2} \cdot 0 + f_{t-1} \cdot 0 \ & = t \cdot f_0 \end{align} $$
所以:
$\sum_{x \in Ht} A(x) = |\vec t| \cdot A(0)$
$\sum{x \in H_f} B(x) = |\vec f| \cdot B(0)$
我们只需要验证下面的关系是否成立:
$|\vec t| \cdot A(0) \stackrel{?}{=} |\vec f| \cdot B(0)$
最终,我们通过这三个证明就完成了 CQ 要证明的 lookup。
致谢
-
Guo Yu
-
Yu-Ming Hsu
-
Jing-Jie Wang
-
Paul Yu
-
Even Lu
参考
[^1ID1]: PSE Acceleration Program: https://github.com/privacy-scaling-explorations/acceleration-program
[^2ID2]: pylookup: https://github.com/luckyyang/pylookup/tree/cq_fk/src/cq
[^3ID3]: Multivariate lookups based on logarithmic derivatives: https://eprint.iacr.org/2022/1530.pdf
撰文:@harryx1x1
编辑:@ziyinlox
- 在 ZK 电路中发现健全性错误的实用指南 14 浏览
- a16z: 我们对 2026 年加密货币领域感到兴奋的 17 件事 805 浏览
- ZK Mesh:2025年12月回顾 277 浏览
- ZK 编年史:多线性扩展 499 浏览
- Celo 上的首个同步可组合的 Appchain 496 浏览
- 从零开始构建 ZK (STARK) 证明器的旅程 429 浏览
- Base-Solana 桥梁工程 481 浏览
- 通过设计实现自主性: 在后界面世界中维护用户控制权 231 浏览
- 安全研究人员的数学指南 510 浏览
- ZK编年史:电路(第一部分) 542 浏览
- ZK Rollup 开发公司:构建可扩展、私密和高速的 Web3 解决方案 355 浏览
- 密码朋克人物传之《Zcash创始人 Zooko Wilcox-O'Hearn》 911 浏览

