Circom 常见陷阱及规避方法 — 第 1 部分 - ZKSECURITY

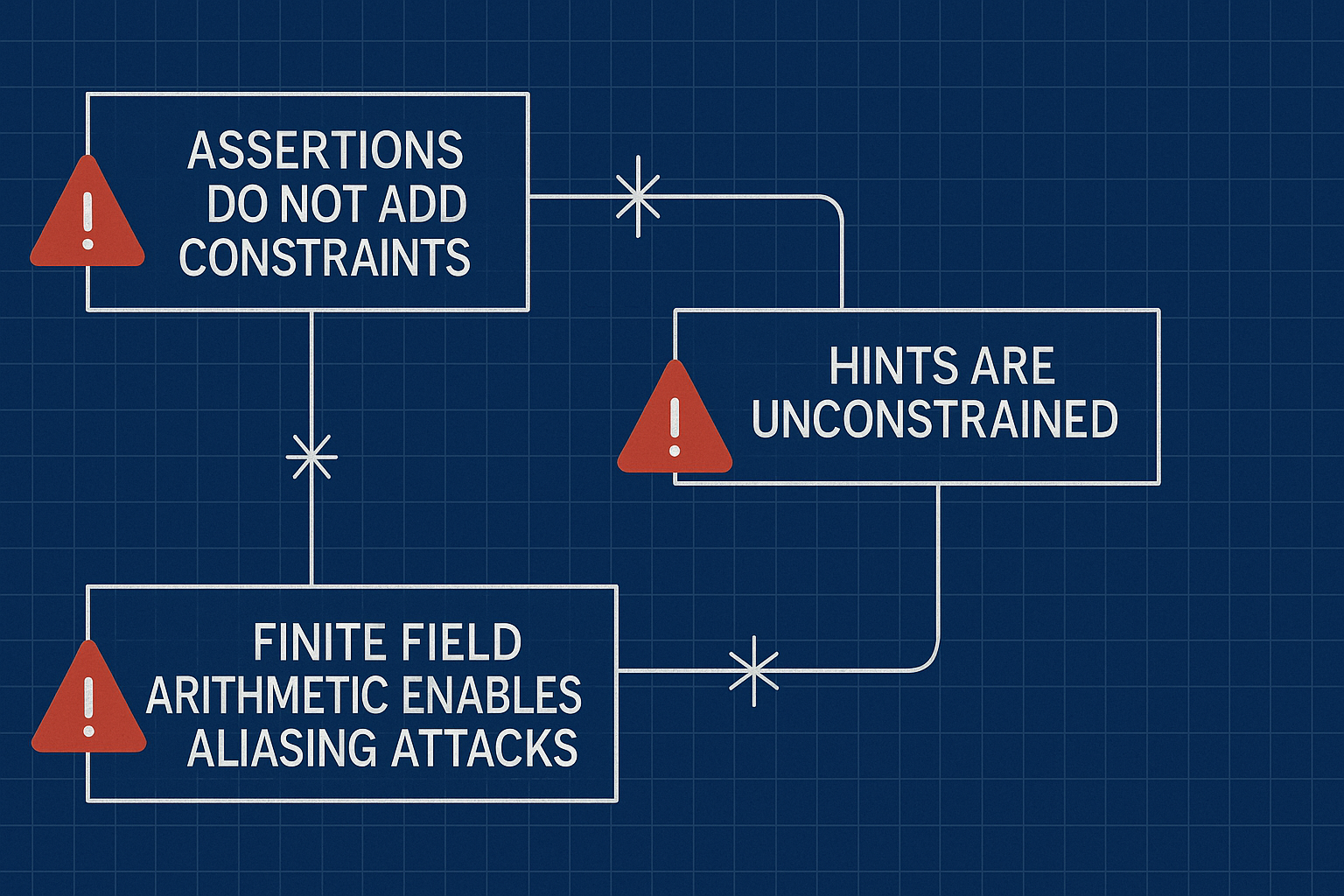
使用 Circom 编程会遇到相当多的挑战。在审查了大量的 Circom 代码库后，我们发现了一些经常出现的反模式。

在本系列中，我们将全面概述这些问题，以帮助你避免最常见的陷阱。

当然，这不会是所有可能错误的完整列表（Circom 有很多让你绊倒的方法）。但我们将介绍的这些 埋雷点 是最容易让开发者措手不及的。因此，让我们分解它们，更重要的是，学习如何躲避它们。

断言不会添加约束

Circom 的 assert 不会向电路底层的 R1CS 添加约束。因此，你永远不应该使用 assert 来代替 ===！

Circom 断言 的唯一目的是添加安全检查，以确保模板不会被实例化为不需要的编译时参数。例如，circomlib 使用 assert 来确保开发者只能使用 LessThan(n) 模板，且 n <= 252，因为使用 n = 253 实例化 LessThan(n) 可能会导致别名错误。（如果你以前从未听说过别名错误，请不要担心！我们稍后会介绍这些。）

template LessThan(n) {
    // 确保开发者无法使用 n > 252 编译此模板
    assert(n <= 252);
    signal input in[2];
    signal output out;

    component n2b = Num2Bits(n+1);

    n2b.in <== in[0]+ (1<<n) - in[1];

    out <== 1-n2b.out[n];
}

人们错误地使用 assert 的部分原因可能是，即使是相对较新的 AI 模型也会犯错：

当被问及 “在 Circom 中使用 assert 的实际用例是什么？” 时的 o3-mini-high 输出

这个建议是 江湖骗术。Circom 的 assert 应该只应用于 模板参数，而不是信号。

然而，令人困惑的是，你实际上 可以 在 Circom 中将 assert 应用于信号。更糟糕的是，将 assert 应用于信号的结果看起来非常像应用 === 的结果！例如，考虑 zkrepl.dev 中的以下电路：

pragma circom 2.1.6;

template TwoBools () {
    signal input a;
    signal input b;

    (a - 1) * a === 0;
    (b - 1) * b === 0;
}

component main = TwoBools();

/* INPUT = {
    // A valid boolean
    "a": "1",
    // Not a valid boolean
    "b": "42"
} */

运行此代码将产生以下错误，因为将 b 的输入设置为 42 违反了第二个约束。

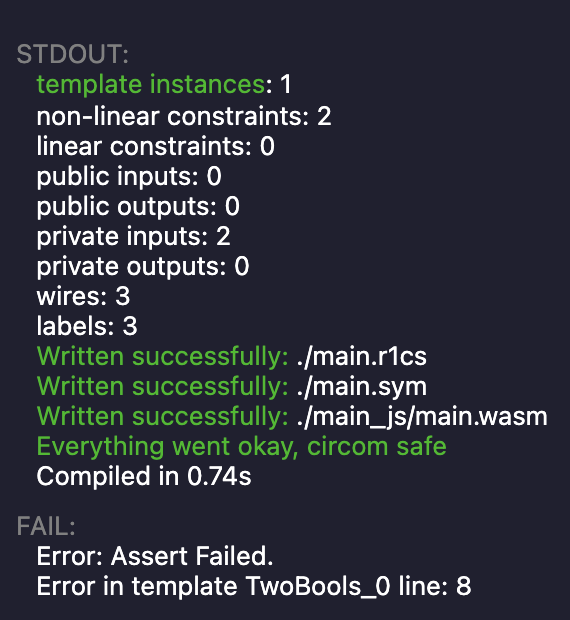
好的，到目前为止没有意外。但是，如果我们用断言替换 (b - 1) * b === 0 会发生什么？

pragma circom 2.1.6;

template TwoBools () {
    signal input a;
    signal input b;

    (a - 1) * a === 0;
    // 使用 `assert` 而不是 `===`
    assert((b - 1) * b == 0);
}

component main = TwoBools();

/* INPUT = {
    "a": "1",
    "b": "42"
} */

运行这段代码实际上会产生相同的错误！

因此，乍一看，使用 assert 和 === 看起来没什么坏处。但是，这里有一个细微的差别：我们电路的 R1CS 现在只有一个约束，而不是两个！

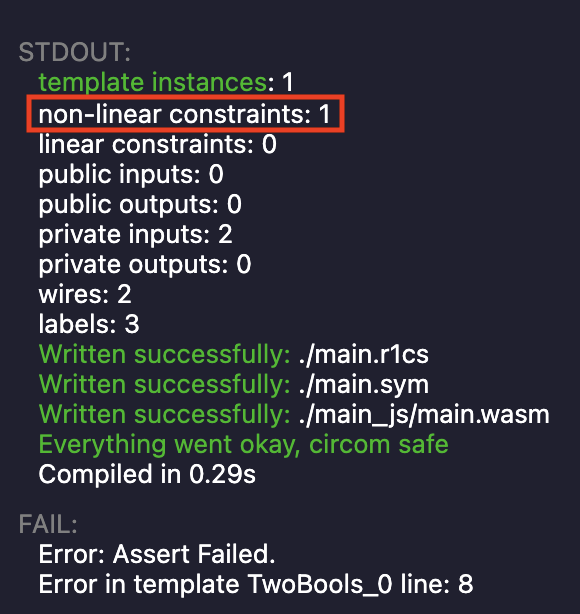
因此，虽然在开发过程中使用 assert “感觉与 === 相同”，但你应该始终假设恶意证明者最终可以复制电路代码，删除 assert，并创建一个证明。请注意，这个恶意证明将满足你电路的所有约束，因为你的 assert 从一开始就没有添加适当的约束！

底线：仅在模板参数上使用 assert，以确保你的模板不是使用不需要的参数值创建的。不要在信号上使用 assert，尤其不要使用 assert 来代替 ===。

提示是不受约束的

Circom 的 <-- 运算符有很多名称：

• 提示 (hint)
• 电路外计算 (out-of-circuit computation)
• 赋值 (assignment)
• 见证生成 (witness generation)
• …

无论你怎么称呼它，如果你在代码中使用此运算符，都应该敲响警钟！原因是什么？

Circom 的 <-- 不会向电路添加任何约束！

将 <-- 运算符视为“接受不受信任的用户输入”，必须始终通过添加约束来清理。

一个流行的例子是不受约束的除法：

template Inverse() {
  signal input in;
  signal output out;

  out <-- 1 / in;
}

可以说，这是一个 非常 简单的例子，即使是初级开发人员也应该能够快速识别出上述电路缺乏约束：

template Inverse() {
  signal input in;
  signal output out;

  out <-- 1 / in;

  // 不要忘记约束你的电路外计算！
  out * in === 1;
}

现在你可能会说“嗯，废话…… 为什么会有人掉进这个 坑？！” 但请放心：现实世界的电路很少这么简单。

让我们更进一步，考虑以下电路：

template IsZero() {
  signal input in;
  signal output out;
  signal inv;

  inv <-- in!=0 ? 1/in : 0;
  out <-- -in*inv +1;
  out === -in*inv +1;
}

与我们的 Inverse 示例相比，识别这里的问题 已经 稍微具有挑战性了，不是吗？毕竟，我们的三个信号都出现在约束中，所以我们应该没问题，对吧？对吗？

嗯…… 不。

我们必须添加第二个约束 in * out === 0。否则，攻击者可以轻松地构造一个恶意见证，例如 in = 42，inv = 0，out = 1，验证者会很乐意接受，因为它满足电路的唯一约束 out === -in*inv +1。但是，42 显然是非零的。换句话说，验证者会认为用户有一个零值，而实际上他们没有！

对 Circom 赋值 使用 <-- 而不是 <== 可能很诱人，尤其是因为这会消除编译器可能抛给你的任何“不允许非二次约束！”错误。此外，通过使用提示来分离计算和约束通常比单独使用纯约束来建模计算更有效。特别是，你希望在计算难以执行但易于使用加法和乘法检查的情况下使用 <--。这种电路的一个例子是上面提到的 Inverse 模板。

底线：如果你在 Circom 代码中使用 <--，请绝对确保所有必需的约束都在电路的其他地方显式强制执行！

有限域算术启用别名攻击

如果数字大于 p−1，其中 p 表示 Circom 的域素数，则通过位数组对数字进行编码可能会导致别名错误。

更具体地说，别名 是指二进制数组编码的值 ≥p，因此，在模 p 算术下，它“别名”到不同的、较小的域元素，而不是其真正的整数值。

示例。 假设我们使用 3 位数组编码域元素，即我们可以编码的最大无符号整数是 M=23−1=7。此外，假设 p=5。在这种情况下，（小端）数组 [0,1,1] 是 a=6 的编码，在域 F5 中，它是 x=1 的别名（因为 6 mod 5=1）。请注意，0 和 2 也恰好有一个别名（分别是 5 和 7），而其余域元素 3 和 4 没有 别名。这是因为 3+p(=8) 和 4+p(=9) 超过了我们的 3 位编码最大值 M=7。

更一般地说，假设我们使用 n 位数组来编码输入信号 x。此外，令 p≤M 且 m:=M mod p，其中 M=2n−1 是可以用 n 位表示的最大无符号整数。此外，让我们假设 x∈[0,m]。你可以将 m 视为“阈值，超过该阈值，别名的数量减少 1”。（请注意，这与上面的示例一致，在上面的示例中，我们有 m=7 mod 5=2。元素 0、1、2 各有一个别名，而 3 和 4 没有别名。）

在这种设置中，x 将具有

N:=⌊(M−x)/p⌋

个别名 ai。给定这个数字 N，域元素 y∈(m,p−1] 将有 N−1 个别名 a~j。

对于 x∈[0,m]，可以通过以下方式计算别名：

a1=x+1⋅pa2=x+2⋅p⋮aN=x+N⋅p

给定数字 N，则可以通过以下方式计算剩余域元素 y∈(m,p−1] 的别名：

a~1=y+1⋅pa~2=y+2⋅p⋮a~N−1=y+(N−1)⋅p

你应该将区间 [p,M] 视为 “危险区域”，因为 [p,M] 中的每个元素都将别名化 [0,p−1] 中的一个元素。

换句话说，只要我们编码的二进制数组满足 M≥p，我们就有可能引入别名错误。

在实践中，你通常会发现 M 严格介于 p 和 2p 之间，因此某些（但不是全部）域元素可能具有两个有效的表示形式。

为了使事情更具体，让我们检查一下实际 Circom 代码中的攻击。假设我们要证明我们知道十进制数 42 的 254 位表示形式。为此，我们可以天真地使用以下电路：

pragma circom 2.1.6;

template Bits2Num(n) {
    signal input in[n];
    signal output out;
    var lc1=0;

    var e2 = 1;
    for (var i = 0; i<n; i++) {
        lc1 += in[i] * e2;
        e2 = e2 + e2;
    }

    lc1 ==> out;
}

template Alias (n) {
    signal input in[n];
    signal output out;

    component b2n = Bits2Num(n);

    for (var i=0; i<n; i++) {
        b2n.in[i] <== in[i];
    }

    out <== b2n.out;
}

component main = Alias(254);

但是，此电路不健全！要看到这一点，首先要注意

• n=254，
• p 是 Circom 的默认素数，
• 并且 x=42 是我们想要伪造二进制编码的域元素。

请注意，这意味着：

• M=2254−1 且
• m=M mod p≈7.05⋅1075

因此，我们有 x∈[0,m]，因此可以计算：

N=⌊(M−x)/p⌋=1

换句话说：在默认 Circom 中，数字 x=42∈[0,p−1] 恰好有一个别名，即 a=42+p∈[p,M]。特别是，我们可以说服验证者 a 的二进制表示是 x 的二进制表示 — 而实际上并非如此！

要查看电路是否确实不健全，你可以在 zkREPL 中运行以下示例：

pragma circom 2.1.6;

template Bits2Num(n) {
    signal input in[n];
    signal output out;
    var lc1=0;

    var e2 = 1;
    for (var i = 0; i<n; i++) {
        lc1 += in[i] * e2;
        e2 = e2 + e2;
    }

    lc1 ==> out;
}

template Alias (n) {
    signal input in[n];
    signal output out;

    component b2n = Bits2Num(n);

    for (var i=0; i<n; i++) {
        b2n.in[i] <== in[i];
    }

    out <== b2n.out;
}

component main = Alias(254);

// 使用 42+p 的（小端）二进制表示作为输入 'in'

/* INPUT = {
    "in": [1,1,0,1,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,0,0,1,0,0,1,1,0,1,0,1,1,1,1,1,0,0,0,0,1,1,1,1,1,0,0,0,0,1,0,1,0,0,0,1,0,0,1,0,0,0,0,1,1,1,0,1,0,0,1,1,1,0,1,1,0,0,1,1,1,1,0,0,0,0,1,0,0,1,0,0,0,0,1,0,1,1,1,1,1,0,0,1,1,0,0,0,0,0,1,0,1,0,0,1,0,1,1,1,0,1,0,0,0,0,1,1,0,1,0,1,0,0,0,0,0,0,1,1,0,0,0,0,0,0,1,0,1,1,0,1,1,0,1,1,0,1,0,0,0,1,0,0,0,0,0,1,0,1,0,0,0,0,1,1,1,0,1,1,0,0,1,0,1,0,0,0,0,0,0,0,1,0,1,1,0,0,0,1,1,0,0,1,0,0,0,0,1,1,1,0,1,0,0,1,1,1,0,0,1,1,1,0,0,1,0,0,0,1,0,0,1,1,0,0,0,0,0,1,1]
} */

// 'out' 将评估为 42，尽管 'in' 不是 42 的正确二进制
// 表示形式（应该是 [0,1,0,1,0,1,0,0,0,...]）

好的，现在我们对别名攻击有了更好的理解，我们如何防止它们？ 亲爱的华生...

对于默认情况，其中 p 是 Circom 的默认素数且 n=254，circomlib 提供了 Bits2Num 和 Num2Bits 的 “严格” 版本，它们实现了一个 AliasCheck 以 “切断” 危险区域 [p,M]，使其与区间 [0,M] 分离。换句话说，这些模板将确保输入严格小于域素数，以便始终拒绝别名输入。

template AliasCheck() {

    signal input in[254];

    component  compConstant = CompConstant(-1);

    for (var i=0; i<254; i++) in[i] ==> compConstant.in[i];

    compConstant.out === 0;
}

template Bits2Num_strict() {
    signal input in[254];
    signal output out;

    component aliasCheck = AliasCheck();
    component b2n = Bits2Num(254);

    for (var i=0; i<254; i++) {
        in[i] ==> b2n.in[i];
        in[i] ==> aliasCheck.in[i];
    }

    b2n.out ==> out;
}

template Num2Bits_strict() {
    signal input in;
    signal output out[254];

    component aliasCheck = AliasCheck();
    component n2b = Num2Bits(254);
    in ==> n2b.in;

    for (var i=0; i<254; i++) {
        n2b.out[i] ==> out[i];
        n2b.out[i] ==> aliasCheck.in[i];
    }
}

请注意，AliasCheck 模板使用 CompConstant(-1) 来强制二进制输入数组编码的值小于或等于 p−1(=−1 mod p)。

在结束之前，我们想再次强调，只有在 M≥p 的情况下才会发生别名攻击。换句话说，如果输入的位大小允许对大于域素数的数字进行二进制编码。这正是 circomlib 的 LessThan(n) 模板强制执行 n <= 252 的原因：大于该值将导致实例化 LessThan 的内部 Num2Bits，这将容易受到别名攻击。

template LessThan(n) {
    assert(n <= 252);
    signal input in[2];
    signal output out;

    // n > 252 会使 Num2Bits(n+1) 容易受到
    // 别名攻击
    component n2b = Num2Bits(n+1);

    n2b.in <== in[0]+ (1<<n) - in[1];

    out <== 1-n2b.out[n];
}

最后，请注意 circomlib 的 AliasCheck、CompConstant、Bits2Num_strict 和 Num2Bits_strict 都将位大小硬编码为 254！ 这意味着，如果你决定使用 Circom 默认的 254 位以外的域素数，你可能必须相应地手动更改这些模板以防止别名攻击。

有关别名漏洞的真实示例，请查看以下（已修复的）Semaphore 中的双重支出问题。

底线：如果 n = 254 且 p 是 Circom 的默认素数，则使用 circomlib 的 Bits2Num(n) 和 Num2Bits(n) 模板可能会使你的电路容易受到别名攻击。 为了缓解此问题，你可以改用这些模板的 circomlib _strict 版本。

_特别感谢 Gregor Mitscha-Baude、Alex Babits、Giorgio Dell’Immagine、Nadir Khan、金宰勋 (Jaehun Kim) 和 0xAlexSR 花费宝贵的时间帮助我润色这篇文章。_

• 原文链接： blog.zksecurity.xyz/post...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～