Arweave 第 17 版白皮书解读(二):数据索引, 唯一副本与 VDF
- PermaDAO
- 发布于 2024-03-28 15:24
- 阅读 2836
本文将介绍 Arweave 最新白皮书的第三节。这一部分主要是对一些基础性概念作一些解释,为此后机制的介绍作好铺垫。本来这部分还包括了 SPoRes 的机制论证,由于全是公式与数学推导过程,笔者觉得也许单独拎出来解读会更加合理一些。
 作者: Arweave Oasis
作者: Arweave Oasis
原文链接:https://twitter.com/ArweaveOasis/status/1771021556258689301*
本文将介绍 Arweave 最新白皮书的第三节。这一部分主要是对一些基础性概念作一些解释,为此后机制的介绍作好铺垫。本来这部分还包括了 SPoRes 的机制论证,由于全是公式与数学推导过程,笔者觉得也许单独拎出来解读会更加合理一些。
Arweave 的挖矿机制将许多不同的算法和数据结构组合成一个非交互式且简洁的数据复制存储证明。在本文中,我们先抽象地理解机制概念,然后再对它们在 Arweave 挖矿过程中的使用进行描述。
区块索引
Arweave 中最高的数据结构被称为区块索引(Block Index)。它是一个由三元组(3-tuples)组成的默克尔化列表,每个元组包含三个维度的信息,即区块哈希(A Block Hash)、编织网络大小(A Weave Size)和交易根(A Transaction Root)。这个列表以一个哈希默克尔树的形式来表示,顶层的默克尔根代表了网络中当前的最新状态。这个根是由两个元素的哈希组成——最新的元组(代表最新区块)和前一个区块索引的默克尔根。在创建区块时,矿工将前一个区块索引的默克尔根嵌入在新区块中。
通过在每个区块中构建并嵌入一个区块索引的默克尔根,一个已对最新区块执行了 SPV 证明的 Arweave 网络节点能够完全验证任何之前的区块。这与传统的区块链形成对比,在传统区块链中,验证旧区块中的交易需要回溯整个链进行完整验证。而在 Arweave 中,在对网络顶端进行 SPV 验证之后,区块索引验证机制能够让用户在对网络顶端进行 SPV 验证之后就可验证编织网络中的旧区块,而不再需要用户下载或验证中间的区块头。
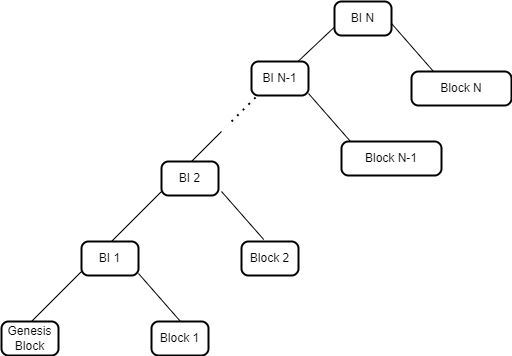
图 1:区块索引代表了 Arweave 网络中区块的一个默克尔树
默克尔化数据
那数据是如何被存储在网络中的呢?
当信息需要被存储到 Arweave 时,数据会根据规范被切分成 256 KB 的一个个数据块(Chunk)。这些数据块在准备好之后,就会构建一个默克尔树,并将其根(称为数据根 Data Root)提交到交易中。该交易被签名并由上传者发送到网络。每个这样构建的交易都被记录在其所属区块的交易根( Transaction Root)里。因此,一个区块的交易根实际上是交易数据根的默克尔根。
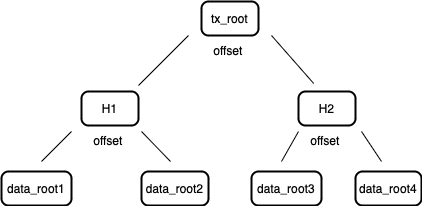
图 2:交易根是区块内每个交易中存在的数据根的默克尔根。
矿工将这样的交易组合成一个区块,使用交易内的数据根计算交易根,并将这个交易根包含在新区块中。这个交易根最终会出现在顶层的区块索引中。该过程创建了一个不断扩展的默克尔树,其中所有数据都按顺序被分成了数据块。
简洁的访问证明 SPoA
在 Arweave 网络里,默克尔树中的节点通过标记数据在节点“左侧”或“右侧”的偏移位置来对数据块进行标记。这种对节点的标记方法可以生成非常简洁的默克尔证明,用来验证数据集在特定位置上的数据块的存在性。这类默克尔树被称作“不平衡树”,因为节点一边的叶节点数可能不等于另一边。这种结构可以用来构建一个简洁的非交互式证明游戏,用以验证矿工硬盘中确实有相应的数据。
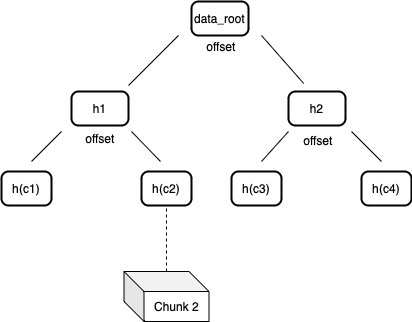
图 3:数据根(data root)是单个交易中所有数据块经过哈希处理的的默克尔根。
我们通过 Bob 与 Alice 的游戏来理解什么是简洁的访问证明(Succint Proof of Access SPoA)。Bob 想要验证 Alice 是否在一个默克尔化数据集的特定位置存储了数据。为了开始游戏,Bob 和 Alice 应该拥有相同的数据集的默克尔根。游戏分为三个阶段:挑战、证明构建和验证。
- 挑战:Bob 向 Alice 发送了一个数据块的偏移量(也许理解成数据块位置坐标会更清晰一点)来发起挑战 —— Alice 需要证明她能够访问这个位置索引的数据。
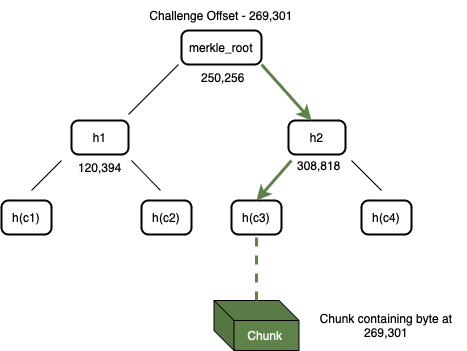
图 4:Alice 可以通过遍历带有偏移量标签的默克尔树来搜索挑战的数据块(Chunk)
- 构建证明:收到这个挑战后,Alice 开始构建证明。她搜索自己的默克尔树,找到与偏移量对应的数据块,如图 4 所示。 在构建证明的第一阶段,Alice 从存储中检索到整个数据块。然后,她使用该数据块和默克尔树构造一个默克尔证明路径。她对整个数据块进行哈希处理,以获得一个 32 字节的字符串,并在树中找到这个叶节点的父节点。父节点是一个包含其偏移量和两个子节点的哈希值的节点,每个哈希值都是 32 字节长度。这个父节点被添加到证明中。然后递归地将每个上层的父节点添加到证明中,直到达到默克尔根。这一系列节点形成了默克尔路径证明,Alice 将这个证明连同数据块一起发送给 Bob。
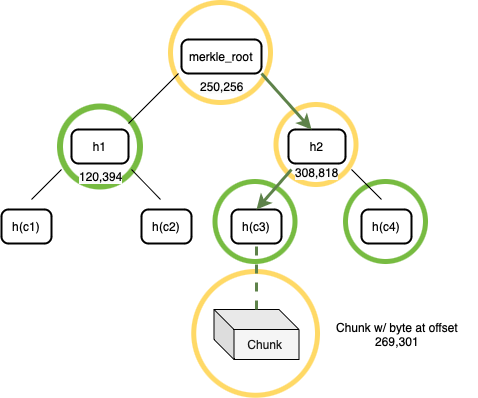
图 5:一个挑战偏移量的证明包括了存储在偏移量处的数据块及其默克尔路径
- 验证:Bob 接收到了来自 Alice 的默克尔证明以及数据块。他通过一步步检查从树顶端到底部叶子的哈希值来核实默克尔证明的正确性。接着,他会对 Alice 提供的证明中的数据块进行哈希运算,确认这个数据块是否正是位于正确位置的那个数据块。如果这些哈希值都对得上,就说明证明是有效的。但是,如果在验证过程中发现任何哈希值不符,Bob 就会立即停止检查,并断定 Alice 的证明是无效的。这个检验的结果是个简单的是或否的过程,表明证明是否通过。
构造、传输和验证这个简洁访问证明(SPoA)的复杂度是 O(logn),其中 n 代表数据集的大小,以字节计。实际上,这意味着在一个大小为 2 的 256 次方字节的数据集中,一个单字节的位置和正确性的证明可以仅通过 256 * 96B(最大路径大小)+ 256 KB(最大数据块大小)≈ 280 KB 来传输。
副本的唯一性
Arweave 网络将挖矿能力设计为与矿工(或一组合作的矿工)可以访问的编织网络副本数量成正比。在没有副本唯一性方案的情况下,一份数据的备份在内容上彼此完全相同。为了激励并衡量单个数据的多个唯一副本,Arweave 使用了一种打包(Packing)系统来解决这个问题。
打包 Packing
打包机制确保了矿工无法用同一个数据块来伪造多个 SPoA 证明。Arweave 引用了 RandomX 打包方案,将原始数据块转换为「打包」的数据块,这个过程会为矿工带来一定的计算成本。
打包的流程如下:
- 数据块偏移量、交易根和挖矿地址被用于一个 SHA-256 哈希中,来生成一个打包密钥 Packing Key。
- 打包密钥被用作算法的熵,该算法在几轮 RandomX 执行后生成一个 2 MB 的暂存器。这个打包机制的组成部分对于不遵守规则的矿工来说带来了重大成本。
- 这个熵的前 256 KB 被用来通过费斯妥密码(Feistel cypher)对块进行对称加密。通过运算产生出一个打包数据块。
如果在连续读取的时间周期内,打包数据块的总成本超过了存储已打包数据块的成本,那么矿工将被激励去存储唯一的数据块,而不是按需打包数据块。所以为了激励这种正确的行为,就必须满足以下条件:
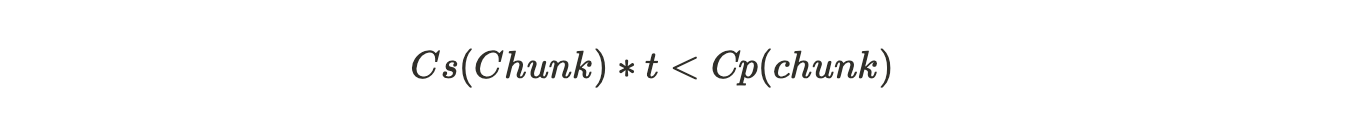
其中:
Cs= 存储一个数据块的单位时间成本
Cp= 打包一个数据块的成本
t= 数据块读取之间的平均时间
其中打包总成本包括了计算所需的电力成本、专用硬件成本及其平均使用寿命。存储成本同样可以从硬盘成本、硬盘平均故障时间、运行硬盘的电力成本以及与运行存储硬件相关的其他成本中计算得出。我们可以计算「按需」投机挖矿者与存储打包数据块的诚实挖矿者的成本比率,以估算激励打包数据块的安全边际。实践中,Arweave 使用一个安全比率——即按需投机挖矿的成本与存储数据诚实挖矿的成本比率——在撰写本文时,大约为 19:1。
RandomX
为了抵抗硬件加速策略,Arweave 采用了哈希算法 RandomX 对打包密钥进行处理。RandomX 针对通用 CPU 进行了优化,通过在哈希过程中实行随机代码执行和多种内存密集型技术,极大限制了专用硬件如 GPU 与 ASIC 的计算效率。
RandomX 利用随机生成的程序,与通用型 CPU 的硬件特性进行高度匹配,这便意味着要想提高 RandomX 哈希速度的唯一方法就是开发出更快的通用 CPU。这也许在理论上会是促进更快 CPU 的开发动机,但实际上相对于已有的提升 CPU 速度的动机,这点激励带来的影响几乎可以忽略不计。
可验证延迟函数 VDF
可验证的延迟函数(Verifiable Delay Function VDF)就像一个具有可验证性的加密数字时钟,它允许对事件之间的时间流逝进行计算验证。VDF 需要执行指定数量且按顺序非并行的哈希计算来产生一个独特又能高效验证的输出。Arweave 协议使用了一种叫链式哈希(Hash Chain)的技术来生成 VDF,其递归定义为:
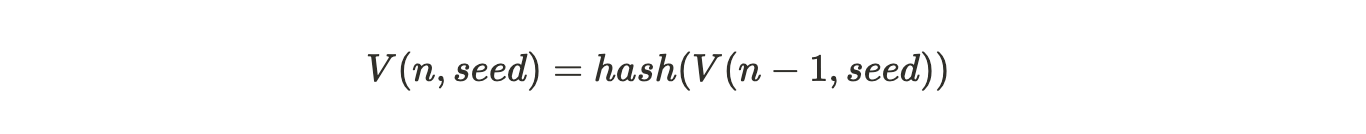
公式注解:第 n 个 VDF 哈希是对其前一个 VDF 哈希的再哈希处理
对于 n = 1 时:
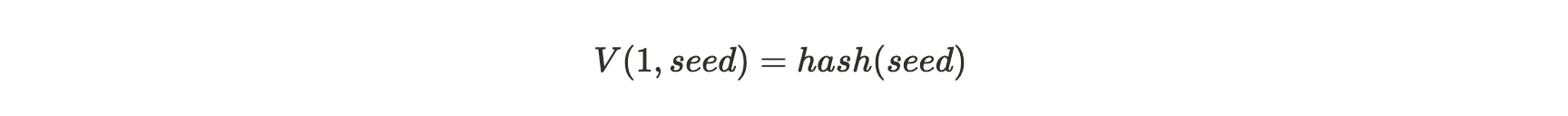
公式注解:如果 n=1,也就是第一个 VDF 哈希是对种子的哈希计算
Arweave VDF 使用的哈希函数是 SHA2-256。通过这种结构,如果市面上最快的 CPU 处理器每秒能连续计算 k 个 SHA2-256 哈希值,那么对一个种子(seed)进行 V(k,seed) 计算就至少需要 1 秒时间。这是一个连续哈希的过程,如上述公式所示,当 n=1 时,对 Seed 进行哈希计算,当 n=2 时,V(2,seed)是对 V(1,seed)的哈希计算,以此类推。一个正确生成的 V(k,seed) ,称为检查点(Checkpoint),意味着证明者接收种子和生成这个检查点之间至少经过了 1 秒时间。
如果 VDF 结构需要 O(n) 时间来完成 n 步的计算,那验证者可以使用 p 个并行线程在 O(n/p) 时间内完成对 VDF 输出的验证。这里需要注意的是,VDF 的生成不准使用并行线程计算,但验证可以,这能够让验证过程变得更加快速且高效。我们之所以使用链式哈希 VDF,是因为它简单的结构,以及完全依赖于哈希函数的稳健性的特性。
- 原创
- 学分: 1
- 分类: Arweave/AO
- 标签: 去中心化存储 数据索引
- 第21章:数据索引与聚合 1398 浏览
- 什么是 Shelby 协议? 791 浏览
- 2026年展望:重构 - Heun的视角 231 浏览
- Web3 与去中心化存储 1995 浏览
- 密码朋克人物传之《Zcash创始人 Zooko Wilcox-O'Hearn》 1334 浏览
- 📦 Web3 和区块链中的 IPFS:何时使用以及何时不使用 2566 浏览
- Solana 数据索引的问题 2987 浏览
- Walrus 协议 (WAL) 是什么 - 综合概述 1199 浏览
- 4EVERLAND 代币经济学:为全球 Web3 计算建立基础价值支柱 1861 浏览
- 去中心化存储的时空证明机制本质原理 4046 浏览
- 从索引协议到 AI 基础设施:The Graph 的故事 1452 浏览
- 如何在 Permaswap 提供流动性赚钱 2893 浏览

