专题输出 | EIP-4844 经济学#2: 深入 Rollup 数据可用策略

写在前面

在 EIP-4844 经济学系列中，我们将分四部分来讲述新增的 blob-carrying transaction 会给网络带来何种影响。在上一篇文章中，笔者深入 Blob 交易的费用机制，包括 Blob 交易的费用计算方式，Blob 交易的特质以及 Blob Base Fee 的更新算法等内容。在本篇文章中，笔者基于 EIP-4844 Economics and Rollup Strategies 的分析框架进一步挖掘 EIP-4844 新引入的 Blob 市场会如何影响其主要的需求方 Rollup 的数据可用策略。

EIP-4844 经济学系列：

• EIP-4844 经济学#1: 深入 EIP-4844 费用机制
• EIP-4844 经济学#2: 深入 Rollup 数据可用策略（本文）
• EIP-4844 经济学#3: 深入多维资源定价
• EIP-4844 经济学#4: 深入 Type 3 交易打包策略

Rollup 数据可用策略

EIP-4844 引入了 Blob 数据空间作为更佳的数据可用方案。似乎对于 Rollup 而言，只需要技术性地升级其密码学承诺算法以支持 Blob 即可。然而，除了技术底层的升级外，Rollup 更需要研究如何利用 Blob 来尽可能降低其可用性数据的成本。换而言之，Rollup 需要根据各自的成本曲线以及需求曲线制定其数据可用的策略。

模型假设分析

建模分析的有效性依赖于模型假设。模型假设肯定是无法完全贴近现实，需要做得到抓小放大，关键在于假设的合理性以及对分析的影响。因此，在进行模型推导前，我们先来分析一下本文依赖的一些关键假设。

假设 1：引入隐性的延迟成本

在建模过程中，除了数据可用方法消耗的手续费外，本文还引入了隐性的数据延迟成本。数据延迟成本可能对于大部分人而言不太直觉。举一个极端例子，比如一个 rollup 的 TPS 是每天 1 笔交易，等待这些交易塞满一个 Blob 才提交至 L1 似乎不是一个优秀的策略。

数据延迟成本的隐形来自于其主要关联于用户体验，某些去中心化应用的安全模型，以及某些去中心化应用的活性。

1. L2 的优势在于其之上的交易能够得到 L1 的确认。虽然序列器能够快速返回 L2 交易处理结果，但是若 L2 交易未得到 L1 的确认，中心化的序列器实际上比 Polygon 等 L1 安全性更差。因此，L2 的目标用户理应关注 L2 交易的可用性数据被提交至 L1 事件以判断交易的状态，并依赖该状态进行后续操作。因此，数据延迟越大，用户需要等待时间越长，用户体验越差
2. 以跨 L2 应用为例，此类应用最终的安全性都依赖于被提交至 L1 的 L2 可用性数据。因此，此类应用的一些关键功能需要等待相应的 L2 交易的可用性数据上传后才可以实现。
3. 对于 zkrollup 而言，L2 交易的可用性数据以及有效性证明被提交至 L1 时 L2 交易立即得到 L1 确认。然而，对于 optimistic rollup 而言，L2 交易的可用性数据被提交至 L1 后仍需等待一段挑战期（如 7 天）。在该情况下，似乎 L2 交易的可用性数据的及时提交没那么重要。实际上并不然，因为有一些应用（如 Maker Bridge）会直接执行验证提交至 L1 的 L2 的可用性数据，无需等待挑战期。

假设 2：数据延迟成本与交易等待时长成正比

本文假设数据延迟成本与交易等待时长成正比（线性函数）。现实中，延迟成本应该更适合用非线形的函数进行刻画。例如，

1. 指数函数（延迟成本随时间指数上升）
2. 分段函数（超过某个阈值才引入延迟成本）

相对于上面更精细的刻画，线形函数具有以下优势：

1. 导数是常数，方便建模推导
2. 连续可导，建模过程中的导数运算

同时，线形函数整体上也刻画了交易等待时长越大，数据延迟成本越高的关键特征，满足建模的需求。不同的线性比例也能捕捉拟合非线形函数。

假设 3：智能合约处理可用性数据的 Gas 消耗为常数

本文在 Blob 的可用策略 和 Calldata 和 Blob 间的可用策略 中假设智能合约处理可用性数据的 Gas 消耗为常数，与交易批次中的交易量无关。

在实际场景中，处理可用性数据的 Gas 消耗可能是与交易量成线性关系的。例如，交易批次中全是 L2 → L1 的操作，那么智能合约可能需要逐个处理这些操作，因此 处理可用性数据的 Gas 消耗也会呈线性关系的。

若对处理可用性数据的 Gas 消耗感兴趣，可以以 Scroll 为例进行洞察：https://github.com/scroll-tech/scroll/pull/659。值得注意的是，EIP-4844 之后，计算交易 witness 的 keccak256 消耗的 gas 可以省去。

根据统计数据可以发现，各个 layer 2 处理可用性数据的方式实际上不太一样。下面挑选典型例子进行说明：

1. Optimism 中处理可用性数据 消耗的 Gas 基本与交易批次的大小无关，十分符合本文的假设。

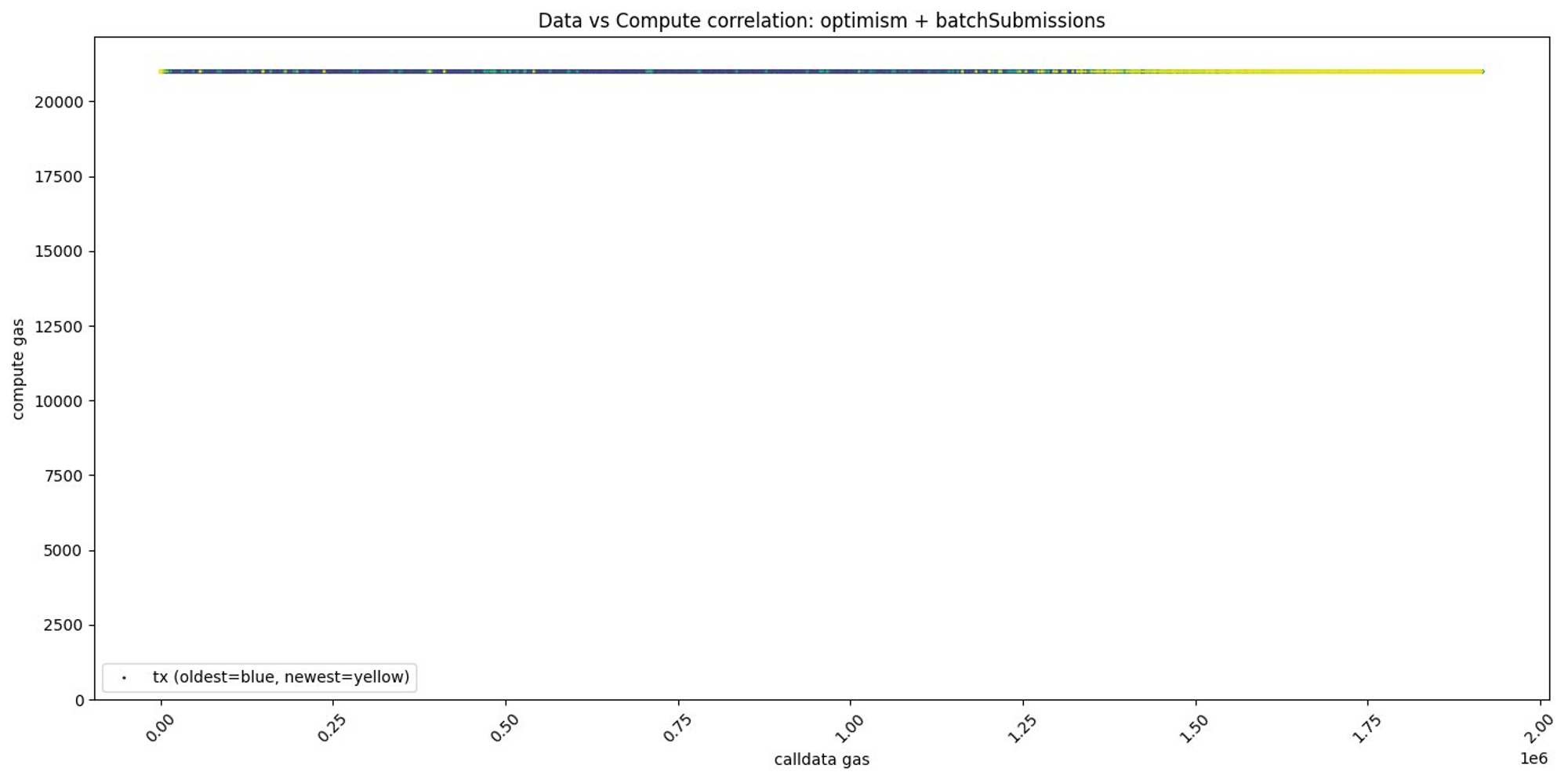cr: @donnoh_eth

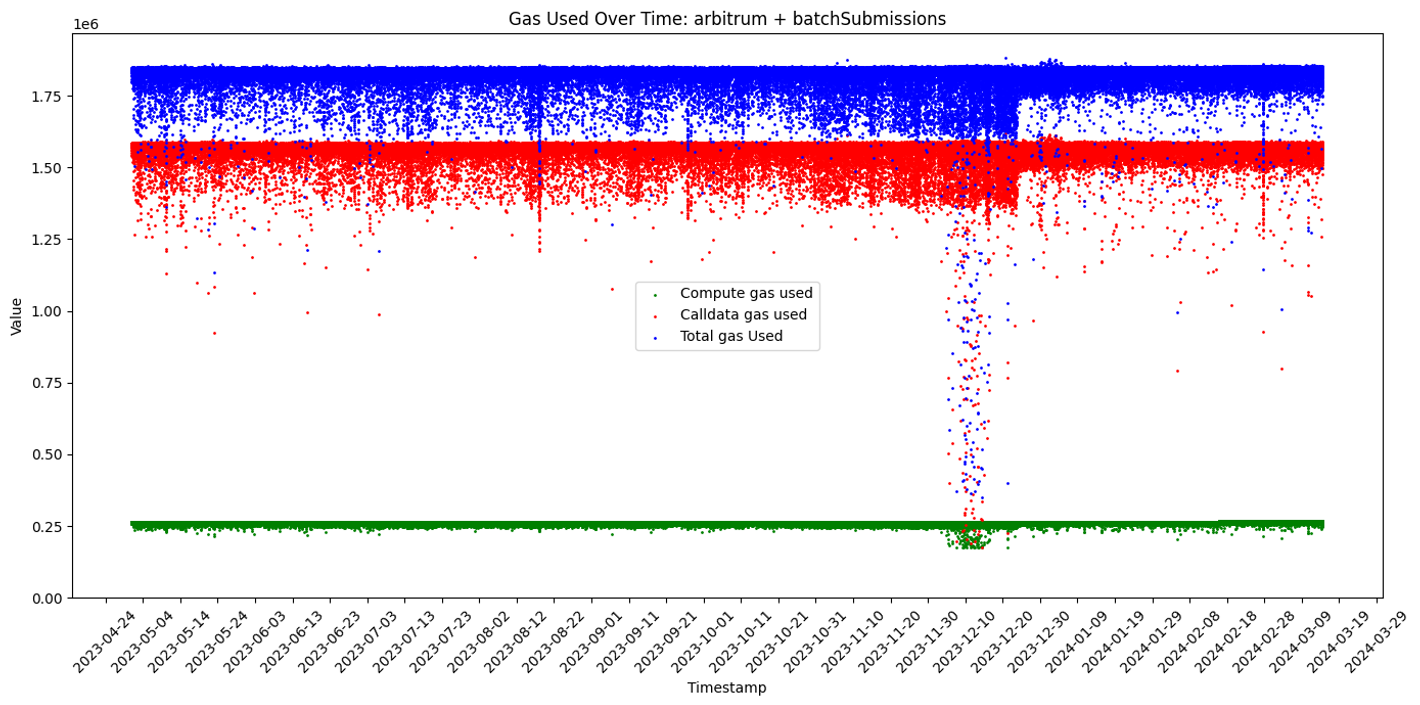
2. Arbitrum 中处理可用性数据 消耗的 Gas 基本与交易批次的大小呈正相关，似乎不太符合本文的假设。固定的部分达到 175000 Gas，可变部分最大达到 90000 Gas，比例约为 51.4%。某种程度而言，该假设仍是合理的。

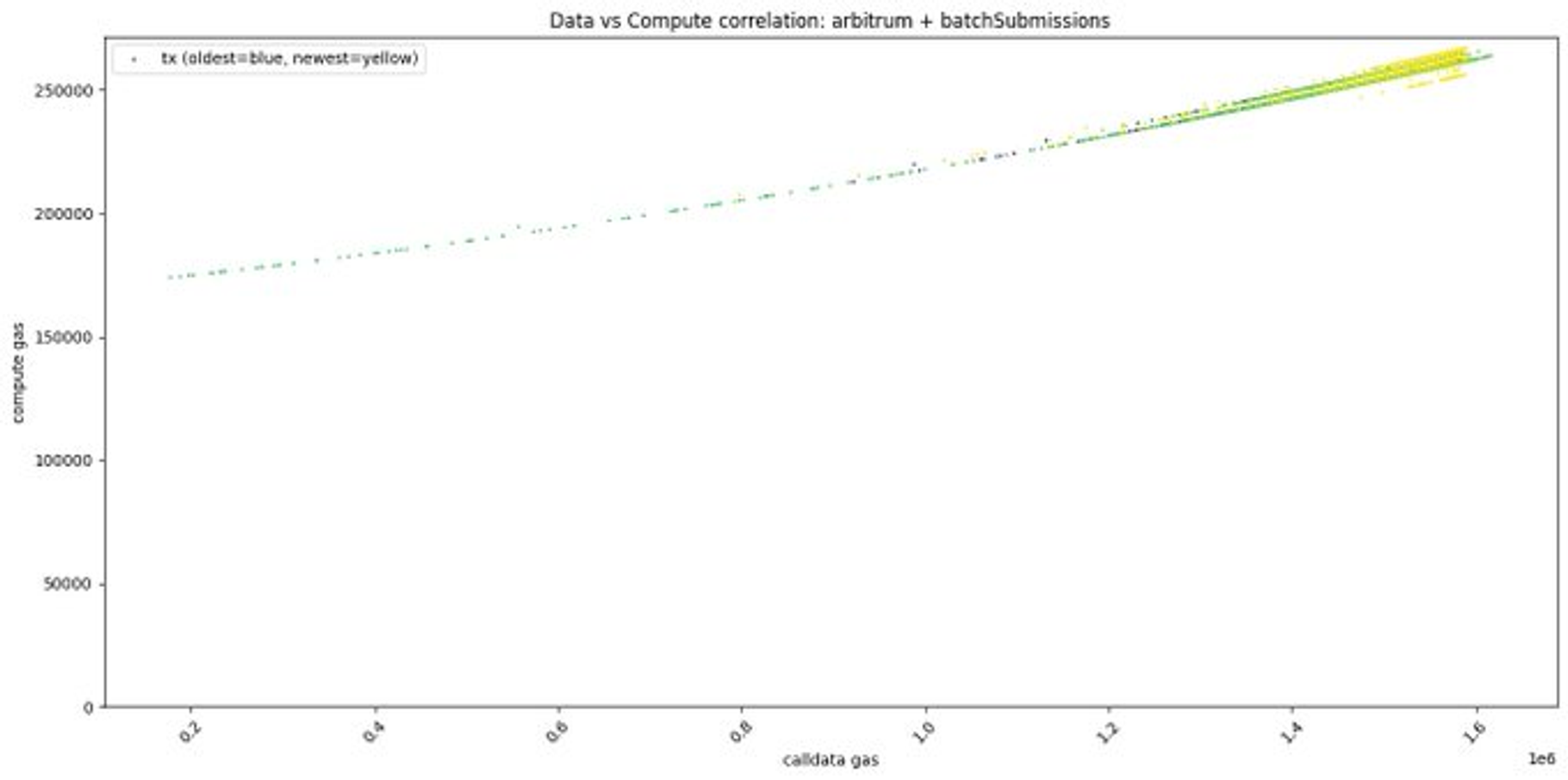cr: @donnoh_eth

假设 4：智能合约处理可用性数据的 Gas 可忽略

本文在 Blob 均衡价格， Blob 拼单策略 以及 Blob 成本分摊 的推导中假设智能合约处理可用性数据的 Gas 消耗可忽略，即远低于上传可用性数据的成本。

在 EIP-4844 之前，根据统计数据，该假设很明显是成立的：

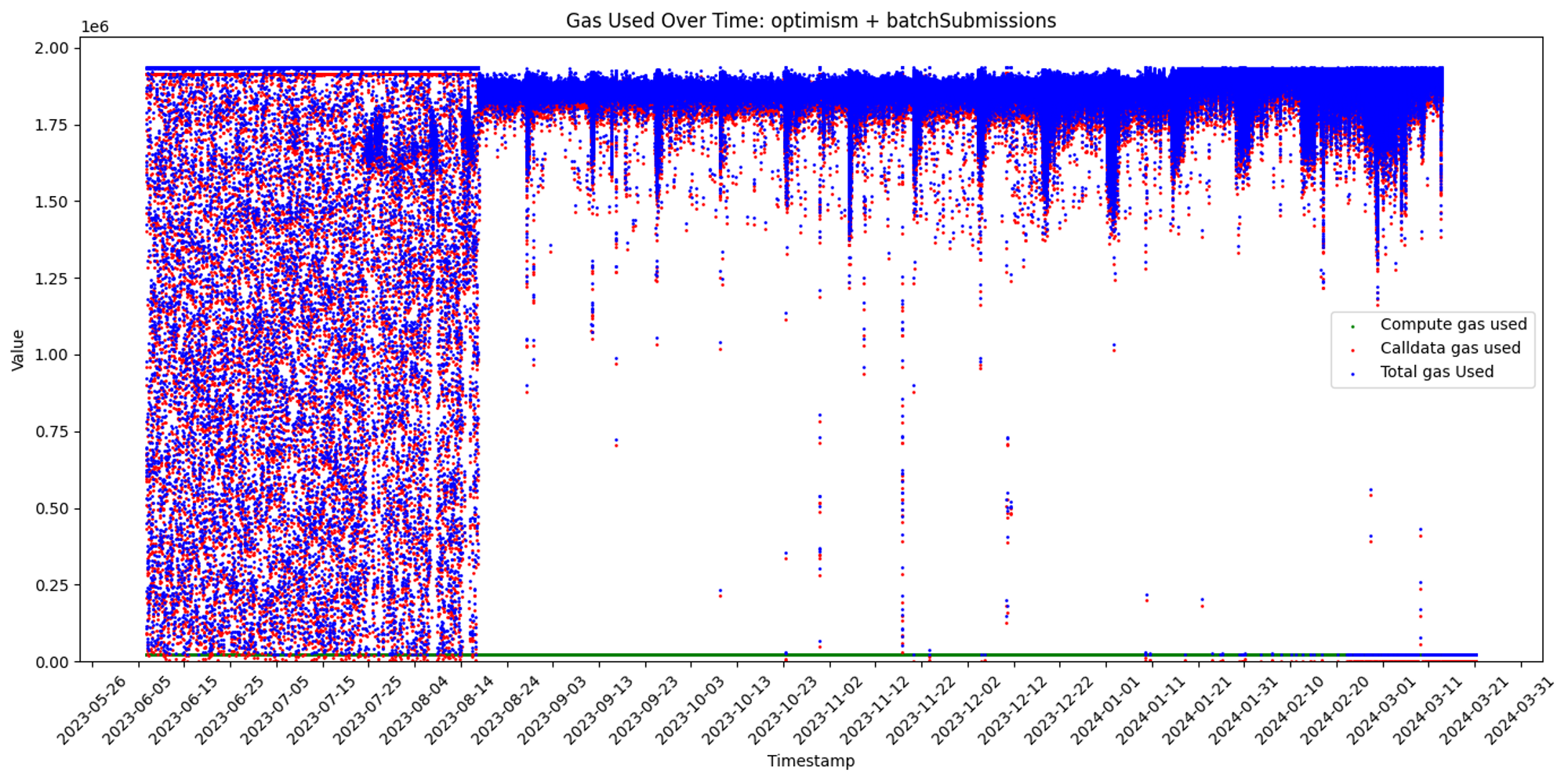cr: @donnoh_eth

cr: @donnoh_eth

然而，EIP-4844 上线前期，Blob 的费用似乎可以忽略不计，参见 Optimism 的一个 batch 交易。这个时期 Blob 的供给远高于需求，Data Gas Price 为 1 wei。

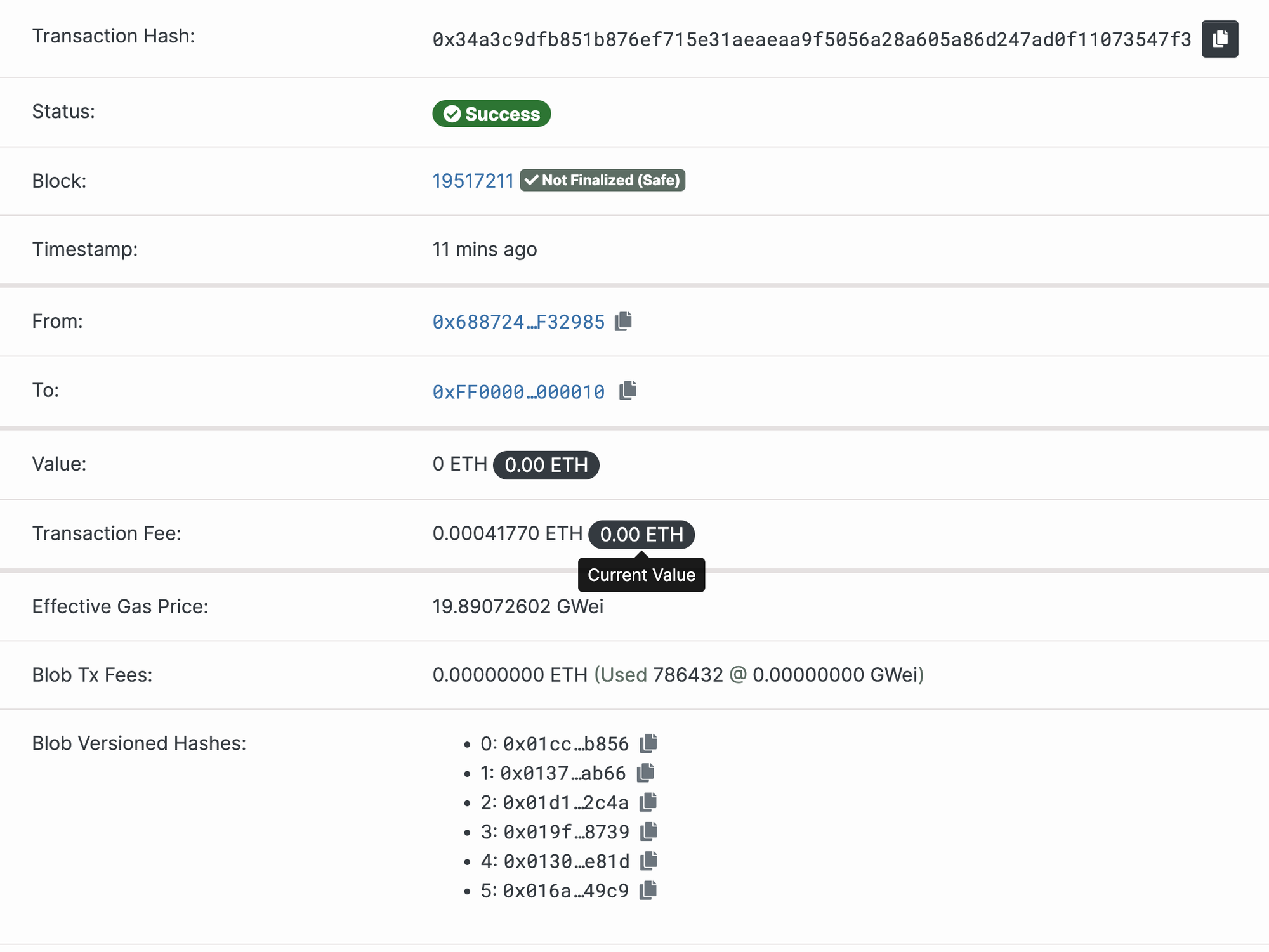cr: beaconcha.in

虽然不符合当前情况，但是该假设在探讨上述三个主题还是有意义的

• Blob 均衡价格 探讨的是 Blob 在未来达到供给需求平衡时的场景
• Blob 拼单策略 以及 Blob 成本分摊 探讨的是 Blob 成本过高而需要拼单的场景

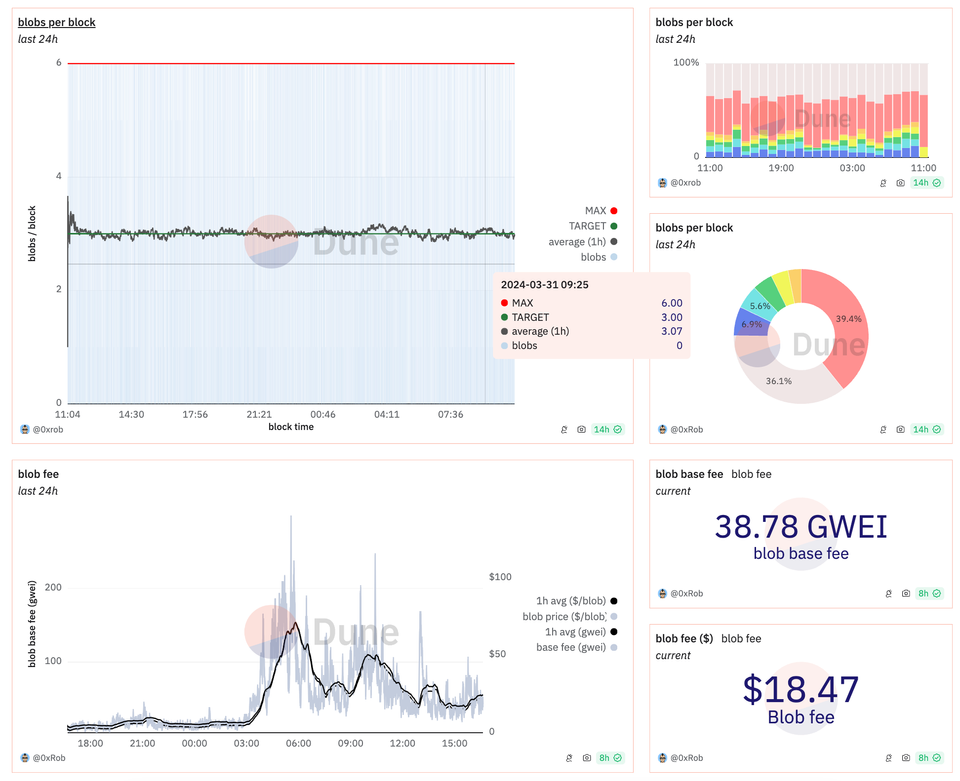
💡 当前（2024.3.31）的 Blob 已经锚定了目标，更接近建模假设：

假设 5：Gas Price 和 Data Gas Price 为静态均衡值

本文在推导的过程中假设 Gas Price 以及 Data Gas Price 为静态均衡值。实际上，均衡值会受供需范式转移的影响，也是动态的。不过，供需范式转移（非随机波动）发生的频率较低。在这中间，均衡值可以考虑为静态值，不会影响在这中间实施的策略。不过，供需范式转移转移后，要更新一下新的状态均衡值即可。

Blob 的可用策略

在 EIP-4844 中，Blob 采用的是集装箱的收费模型。因此，对于 Rollup 而言，需要权衡：

• 当 Blob 被完全利用时，上传可用性数据均摊成本是最低的
• 当 Blob 被完全利用时，数据延迟成本是最高的（等待最长时间才能提交至一层网络）

Blob 数据可用方案成本

已知 Rollup 的交易达到速率为 $R$，交易积累时间 $T$ 后，Rollup 利用 Blob 上传可用性数据。此时，一个 Blob 包含 $RT$ 笔交易。

假设交易的延迟成本与等待时间成正比（比率为 $a$），则 Blob 内交易的总计延迟成本如下

$$ \begin{equation} cost{dealy}(T)=\int{0}^{T}cost(T-t)Rdt=\int_{0}^{T}a(T-t)Rdt=\frac {1}{2}aRT^2 \end{equation} $$

交易的成本分为两个维度：

• 处理可用性数据：假设 Gas Price 固定为 $P$。同时，对于 Rollup 而言，合约处理需要的 Gas 是固定的，可以设为 $G_0$。因此，处理可用性数据成本为 $PG_0$
• 上传可用性数据：假设 Data Gas Price 固定，那么每个 Blob 的交易成本可以设为 $B$。Blob 采用的是集装箱的收费模型。因此，上传可用性数据成本为 $B$

交易的成本如下

$$ \begin{equation} cost^{blob}_{tx}=B+PG_0 \end{equation} $$

Rollup 使用 Blob 作为数据可用方案的成本为

$$ \begin{equation} cost^{blob}(T)=cost{delay}(T)+cost^{blob}{tx} \end{equation} $$

Rollup 中的每笔交易的平均成本为

$$ \begin{equation} F^{blob}(T)=\frac{cost^{blob}(T)}{RT}=\frac{PG_0+B}{RT}+\frac{aT}{2} \end{equation} $$

• 每笔交易需要均摊 处理可用性数据 和 上传可用性数据 的成本
• $F^{blob}(T)$ 的左侧随着 T 单调递减，对应数据均摊成本
• $F^{blob}(T)$的右侧随着 T 单调递增，对应数据延迟成本

$F^{blob}(T)$ 的性质意味着$F^{blob}(T)$存在最小值，即每笔交易的平均成本最低。

令$(F^{blob})^{'}(T)$，可以得到最佳 $T$ 值。

$$ \begin{equation} T^{blob}_{best}=\sqrt{\frac{2(PG_0+B)}{aR}} \end{equation} $$

利用 $T^{blob}_{best}$可以求得每笔交易最低平均成本

$$ \begin{equation} cost^{blob}_{best}=\sqrt{\frac{2(PG0+B)a}{R}}=aT^{blob}{best} \end{equation} $$

此时，一个 Blob 中包含的交易数量为

$$ \begin{equation} N^{blob}{best}=RT^{blob}{best}=\sqrt{\frac{2(PG_0+B)R}{a}} \end{equation} $$

此时，一个 Blob 的总成本为

$$ \begin{equation} Total^{blob}{best}=cost^{blob}{best}N^{blob}_{best}=2(PG_0+B) \end{equation} $$

策略

基于上述建模，对于 Rollup 而言，最佳策略为等待 $T^{blob}_{best}$，然后把交易的可用性数据构造为 Blob 然后发布。

考虑到实际上 Blob 的大小有 128 KB 的限制，填满一个 Blob 的时间为 $T^{blob}_{full}$。

策略调整如下：

• 若 $T^{blob}{best} \le T^{blob}{full}$ ，则 Rollup 等待 Blob 填满立即发布
• 若 $T^{blob}{best} > T^{blob}{full}$ ，则 Rollup 等待 $T^{blob}_{best}$ 立即发布

Calldata 和 Blob 间的可用策略

Blob 作为一种数据可用方案，并非完全优于 Calldata：

• 利用 Calldata 上传可用性数据的均摊成本是不变的，无需如 Blob 般等待数据达到某种量级以降低成本，因此可以做到快速发布，因而有着更低的数据延迟成本。
• 可以预想，有着较少交易量的 Rollup 会更倾向于使用 Calldata。这些 Rollup 需要付出很大的数据延迟成本才能把 Blob 填充完。

Calldata 数据可用方案成本

已知 Rollup 的交易达到速率为 R，交易积累时间 T 后，Rollup 利用 Calldata 上传可用性数据。此时，Calldata 中包含 RT 笔交易。

假设交易的延迟成本与等待时间成正比（比率为 a），则 Calldata 内交易的总计延迟成本如下

$$ \begin{equation} cost{dealy}(T)=\int{0}^{T}cost(T-t)Rdt=\int_{0}^{T}a(T-t)Rdt=\frac {1}{2}aRT^2 \end{equation} $$

交易的成本分为两个维度：

• 处理可用性数据：假设 Gas Price 固定为 P。同时，对于 Rollup 而言，处理可用性数据需要的 Gas 是固定的，可以设为 $G_0$。因此，EVM 维度的成本为 $PG_0$
• 上传可用性数据：假设 Gas Price 固定为 P。同时，对于 Rollup 而言，上传可用性数据需要的 Gas 与交易笔数成正比，可以设为 b。因此，EVM 维度的成本为

$$ \begin{equation} cost^{calldata}_{tx}=PbRT+PG_0 \end{equation} $$

Rollup 使用 Calldata 作为数据可用方案的成本为

$$ \begin{equation} cost^{calldata}(T)=cost{delay}(T)+cost^{calldata}{tx} \end{equation} $$

Rollup 中的每笔交易的平均成本为

$$ \begin{equation} F^{calldata}(T)=\frac{cost^{calldata}(T)}{RT}=Pb+\frac{PG_0}{RT}+\frac{aT}{2} \end{equation} $$

• 每笔交易需要均摊 处理可用性数据 的成本
• $F^{calldata}(T)$ 的左侧随着 T 单调递减，对应数据均摊成本
• $F^{calldata}(T)$的右侧随着 T 单调递增，对应数据延迟成本

$F^{calldata}(T)$ 的性质意味着$F^{calldata}(T)$存在最小值，即每笔交易的平均成本最低。

令$(F^{calldata})^{'}(T)$，可以得到最佳 T 值。

$$ \begin{equation} T^{calldata}_{best}=\sqrt{\frac{2PG_0}{aR}} \end{equation} $$

$$ \begin{equation} T^{blob}_{best}=\sqrt{1+\frac{B}{PG0}}T^{calldata}{best}>T^{calldata}_{best} \end{equation} $$

利用 $T^{blob}_{best}$可以求得每笔交易最低平均成本

$$ \begin{equation} \begin{aligned} cost^{calldata}_{best} &=Pb+\sqrt{\frac{2PG0a}{R}} \ &=Pb+aT^{calldata}{best} \ &=Pb+\frac{1}{\sqrt{1+\frac{B}{PG0}}}cost^{blob}{best} \end{aligned} \end{equation} $$

此时，一个 Blob 中包含的交易数量为

$$ \begin{equation} N^{blob}{best}=RT^{blob}{beste}=\sqrt{\frac{2PG_0R}{a}} \end{equation} $$

令 $cost^{calldata}{best}=cost^{blob}{best}$找出临界 blob 成本 $B_0$，可以得到

$$ \begin{equation} B_0=2Pb(\frac{RPb}{4a}+\sqrt\frac{RPG_0}{2a}) \end{equation}

$$

策略

基于上述建模，对于 Rollup 而言，最佳策略为

• 若 $B \le B_0$，则 Rollup 应该选择 Blob 作为作为数据可用方案
  • Rollup 等待 $T^{blob}_{best}$ 发布 Blob
• 若 $B>B_0$，则 Rollup 应该选择 Calldata 作为数据可用方案
  • Rollup 等待 $T^{calldata}_{best}$ 发布 Calldata

考虑到实际上 Blob 的大小有 128 KB 的限制，填满的时间为 $T^{blob}{full}$。Calldata 的大小 Block Gas Limit 的限制，填满的时间为 $T^{calldata}{full}$。正常而言， $T^{blob}{full}$必定小于 $T^{calldata}{full}$。此时，策略会变得非常复杂，需要具体问题具体分析。

$$ \begin{equation} \begin{array}{l} cost{min}=min{cost^{blob}(T^{blob}), cost^{calldata}(T^{calldata})} \ T^{blob}{full}\ge T^{blob}>0 \ T^{calldata}_{full}\ge T^{calldata}>0 \end{array} \end{equation} $$

下面对现实中的两种主流场景进行说明，这些场景满足 $T^{calldata}{best}\le T^{blob}{full}$：

• 若 $T^{blob}{full} \ge T^{blob}{best}$，那么 $T^{blob}{best}$ 和 $T^{calldata}{best}$ 都是合法的，沿用上面的策略即可。
• 若 $T^{blob}{full} < T^{blob}{best}$，那么 $T^{blob}{best}$ 是非法的，而 $T^{calldata}{best}$ 是合法的
  • 若 $cost^{blob}{full} \le cost^{calldata}{best}$，则 Rollup 应该选择 Blob 作为数据可用方案
    • Rollup 等待 $T^{blob}_{full}$ 发布 Blob
  • 若 $cost^{blob}{full} > cost^{calldata}{best}$，则 Rollup 应该选择 Calldata 作为作为数据可用方案
    • Rollup 等待 $T^{calldata}_{best}$ 发布 Calldata

💡 实际上，主流客户端（如 Geth）限制了交易 128 KB 的大小。不过，该限制非协议层级别的限制。

然而，Vitalik 基于技术的角度更倾向于限制 Calldata 的使用，让 Rollup 都使用 Blob：

• 对于 Rollup 而言，维护两套机制成本太高。
• Calldata 本身不是为数据可用设计的。

关于提高 Calldata 作为数据可用性方案成本的 EIP-7623（Draft）也被提出。基本思路很简单：

1. 若交易 Gas 消耗中 Calldata 的占比 >~ 76%，Calldata 的成本为 68 gas/byte
2. 若交易 Gas 消耗中 Calldata 的占比 < 76%，Calldata 的成本为 16 gas/byte

该 EIP 隐含一个假设，若 Calldata 的占比 >~ 76%，那么该交易就被认定其用于数据可用。该值是通过历史统计权衡出来的：

1. 观察数据可用交易的 Calldata 的占比，尽可能命中
2. 观察非数据可用交易的 Calldata 的占比，尽可能不要误伤

Blob 均衡价格

考虑 Blob 的需求最终锚定了目标值的场景，Blob 的供需达到了均衡状态。

已知有 n 个 Rollup，Rollup i 对应的交易达到速率为 $R_i$。

假设全部 Rollup 都采用 Blob 的策略，根据公式（5），那么 Rollup i 提交 Blob 的时间间隔为

$$ \begin{equation} T_{i}=\sqrt{\frac{2(PG_0+B)}{aR_i}} \end{equation} $$

一般而言，处理可用性数据的成本是可忽略的，因此得到

$$ \begin{equation} T_{i}=\sqrt{\frac{2B}{aR_i}} \end{equation} $$

Blob 均衡价格指的是 Blob 的数量达到目标值的情况。已知 Blob 的目标数量为 $k$，即单位时间链上提交的 Blob 的数量为 k。$k$ 满足以下关系

$$ \begin{equation} k = \sum{i=1}^n\frac{1}{T{i}} \end{equation} $$

因此，得到 Blob 的均衡价格

$$ \begin{equation} B=\frac{a(\sum_{i=1}^n\sqrt{R_i})^2}{2k^2} \end{equation} $$

然而，由于提交 Blob 不一定是 Rollup 的最佳策略。

目前采用 Blob 作为数据可用方案的 Rollup 集合为${R_1,R_2,...,R_n}$，其中 $R_1\ge R_2\ge...\ge R_n$。

把 $R_n$代入公式（16），得到其临界 Blob 成本 $B_0$

• 若 $B \le B_0$，则 Rollup n 应该选择 Blob 作为作为数据可用方案
  • 得到 Blob 均衡价格 B
• 若 $B>B_0$，则 Rollup n 应该选择 Calldata 作为数据可用方案
  • 把 Rollup n 从集合中剔除，得到新集合${R_1,R2,...,R{n-1}}$
  • 循环上述过程，检查 Rollup n-1

💡 实际上可能不存在均衡价格 B，即所有的 Rollup 都选择 Calldata 作为数据可用方案

💡 后续内容均假设处理可用性数据的成本是可忽略的，即 $G_0=0$

Blob 拼单策略

Blob 的联合发布似乎可以解决 Blob 数据延迟成本过高的问题，类比于现实世界的集装箱也不限于只装一家的货物。

本章节评估在下列三种场景下，拼单策略导致 Blob 均衡价格的变化，并分析拼单策略是否相对单独发布为更优策略。

1. Rollup i 和 Rollup j 都采用 Blob 作为数据可用方案
2. Rollup i 采用 Blob 作为数据可用方案，而 Rolup j 采用 Calldata 作为数据可用方案
3. Rollup i 和 Rollup j 都采用 Calldata 作为数据可用方案

💡 已知 $R_j = fR_i$，其中 $1\ge f>0$

场景 1：Rollup i 和 Rollup j 都采用 Blob 作为数据可用方案

场景 1 中 Blob 的均衡价格会降低，最多降低一半

根据公式（22）可以得知未拼单时，Blob 的均衡价格 B 为

$$ \begin{equation} B=\frac{a(\sqrt{R_i}+\sqrt{R_j}+...)^2}{2k^2} \end{equation} $$

Rollup i 和 Rollup j 联合发布 Blob 的均衡价格 $B_{joint}$ 可以表示为下列公式

$$ \begin{equation} B_{joint}=\frac{a(\sqrt{R_i+R_j}+...)^2}{2k^2} \end{equation} $$

B 和 $B_{joint}$ 满足以下关系

$$ \begin{equation} B > B_{joint} \ge \frac{1+f}{(1+\sqrt{f})^2}B \ge B/2 \end{equation} $$

证明

• $\sqrt{R_i}+\sqrt{R_j}=\sqrt{(\sqrt{R_i}+\sqrt{R_j})^2}=\sqrt{R_i+R_j+2\sqrt{R_i}\sqrt{R_j}}>\sqrt{R_i+Rj}$ 得到 $B>B{joint}$。
• $\sqrt{R_i}+\sqrt{R_j}\le\sqrt{2}\sqrt{R_i+Rj}$ 得到 $B{joint}\ge B/2$。
  • $B_{joint}$ 在只有 Rollup i 和 Rollup j，且 $R_i$ 等于$R_j$时，Blob 成本为原来的 1/2
• 综上得到

$$ \begin{equation} \sqrt{2}\ge\frac{1+\sqrt{f}}{\sqrt{1+f}}>1 \end{equation} $$

💡 尝试直观地理解场景 1 中 Blob 均衡价格的变化。 在采用拼单策略前，根据公式（20）可以知道 Rollup i 会每间隔 $1/\sqrt{R_i}$会发布一个 Blob，而Rollup j 会每间隔 $1/\sqrt{R_j}$会发布一个 Blob。因此，单位时间对 Blob 的需求为 $\sqrt{R_i}+\sqrt{R_j}$。 在采用拼单策略后，根据公式（20）可以知道 Rollup i 和 Rollup j 会每间隔 $1/\sqrt{R_i+R_j}$会发布一个 Blob。因此，单位时间对 Blob 的需求为 $\sqrt{R_i+R_j}$，相对于拼单策略前，降低了单位时间对 Blob 的需求。

场景 1 中拼单策略相对单独发布为更优策略

根据公式（8）可以得到拼单后 Blob 的成本

$$ \begin{equation} cost{joint}=2B{joint} \end{equation} $$

根据公式（7）可以得到拼单后 Blob 中交易的数量

$$ \begin{equation} N{joint}=\sqrt{\frac{2B{joint}(R_i+R_j)}{a}} \end{equation} $$

根据公式（6）可以得到拼单前 Rollup i 单笔交易成本

$$ \begin{equation} cost^{blob}_{i}=\sqrt{\frac{2Ba}{R_i}} \end{equation} $$

计算拼单前 Rollup i 若要发布拼单 Blob 内其交易的成本

$$ \begin{equation} cost_i=cost^{blob}i(N{joint}\frac{R_i}{R_i+Rj})=2\sqrt{B{joint}B}\sqrt{\frac{f}{1+f}} \end{equation} $$

类似地计算拼单前 Rollup j 若要发布拼单 Blob 内其交易的成本

$$ \begin{equation} costj=2\sqrt{B{joint}B}\sqrt{\frac{1}{1+f}} \end{equation} $$

Rollup i 和 Rollup j 要发布拼单 Blob 内交易的成本

$$ \begin{equation} cost_{seperate}=cost_i+costj=2\sqrt{B{joint}B}\frac{1+\sqrt{f}}{\sqrt{1+f}} \end{equation} $$

根据公式（25）以及（26）可以得到$cost_{seperate}$的范围

$$ \begin{equation} 4B{joint}\ge2\sqrt{2}\sqrt{B{joint}B}\ge cost{seperate}>2\sqrt{B{joint}B}>2B_{joint} \end{equation} $$

根据公式（33）以及（27）可以得到 $cost{seperate} > cost{joint}$。

综上，在场景一，对于双方而言，拼单策略优于单独发布。

💡 尝试直观地理解该结论。

1. Blob 的均衡价格降低，带来正面影响
2. Rollup 在填充 Blob 所需的延迟成本降低，带来正面影响

场景 2：Rollup i 采用 Blob 作为数据可用方案，而 Rolup j 采用 Calldata 作为数据可用方案

场景 2 中 Blob 的均衡价格会上升，最多为原来的 2 倍

根据公式（22）可以得知未拼单时，Blob 的均衡价格 B 为

$$ \begin{equation} B=\frac{a(\sqrt{R_i}+...)^2}{2k^2} \end{equation} $$

Rollup i 和 Rollup j 联合发布 Blob 的均衡价格 $B_{joint}$ 可以表示为下列公式

$$ \begin{equation} B_{joint}=\frac{a(\sqrt{R_i+R_j}+...)^2}{2k^2} \end{equation} $$

B 和 $B_{joint}$ 满足以下关系

$$ \begin{equation} 2B \ge (1+f)B \ge B_{joint} > B \end{equation} $$

证明

• $\sqrt{R_i}=\frac{1}{\sqrt{2}}\sqrt{R_i+R_i}\ge \frac{1}{\sqrt{2}}\sqrt{R_i+Rj}$ 得到 $2B\ge B{joint}$。
  • $B_{joint}$ 在只有 Rollup i 和 Rollup j，且 $R_i$ 等于$R_j$时，Blob 成本为原来的 2 倍
• $\sqrt{R_i}<\sqrt{R_i+Rj}$ 得到 $B{joint}>B$。
• 综上得到

$$ \begin{equation} \sqrt{2}\ge\sqrt{1+f}>1 \end{equation} $$

在场景 2 下采用拼单策略，由于 Rollup j 原来并不使用 Blob，因此拼单实际上会提高整体对 Blob 的需求，从而提高拼单后 Blob 的均衡价格。

场景 2 中拼单策略相对单独发布不一定是更优策略

根据公式（8）可以得到拼单后 Blob 的成本

$$ \begin{equation} cost{joint}=2B{joint} \end{equation} $$

根据公式（7）可以得到拼单后 Blob 中交易的数量

$$ \begin{equation} N{joint}=\sqrt{\frac{2B{joint}(Ri+R j )}{a}} \end{equation} $$

计算拼单前 Rollup i 若要发布拼单 Blob 内其交易的成本

$$ \begin{equation} cost_i=cost^{blob}i(N{joint}\frac{R_i}{R_i+Rj})=2\sqrt{B{joint}B}\sqrt{\frac{f}{1+f}} \end{equation} $$

根据公式（15）得知 Calldata 的单位交易成本

$$ \begin{equation} cost^{calldata}_{j}=Pb \end{equation} $$

Calldata 的成本对于使用 Blob 的 Rollup i 而言不如 Blob 划算，而对于使用 Calldata 的 Rollup j 而言比 Blob 划算。因此，根据公式（29），Pb 满足如下约束：

$$ \begin{equation} \sqrt{\frac{2Ba}{R_i}}\le Pb \le \sqrt{\frac{2Ba}{R_j}} \end{equation} $$

计算拼单前 Rollup j 若要发布拼单 Blob 内其交易的成本

$$ \begin{equation} cost_j=cost^{calldata}j(N{joint}\frac{R_j}{R_i+R_j})=PbRj\sqrt{\frac{2B{joint}}{a(R_i+R_j)}} \end{equation} $$

根据公式（42）和（43）得到以下约束

$$ \begin{equation} 2\sqrt{B_{joint}B}\sqrt{\frac{f}{1+f}}\sqrt{f} \le cost2 \le 2\sqrt{B{joint}B}\sqrt{\frac{f}{1+f}} \end{equation} $$

Rollup i 和 Rollup j 要发布拼单 Blob 内交易的成本

$$ \begin{equation} cost_{seperate}=cost_i+cost_j \end{equation} $$

根据公式（44）可以得到$cost_{seperate}$的范围约束

$$ \begin{equation} \sqrt{2}B{joint}\le 2\sqrt{B{joint}B}< cost{seperate}\le 2\sqrt{2}\sqrt{B{joint}B}\le2\sqrt{2}B_{joint} \end{equation} $$

根据公式（38）以及（46）可以得知在场景二没有确定性的最优策略

• 当 $cost{seperate} \ge cost{joint}$，对于双方而言，拼单策略是最佳策略。
• 当 $cost{seperate} < cost{joint}$，对于双方而言，拼单策略非最佳策略。

💡 尝试直观地理解该结论。

1. Blob 的均衡价格上升，带来负面影响
2. Rollup i 在填充 blob 所需的延迟成本降低，带来正面影响
3. Rollup j 切换到 blob，带来影响不能一概而论 a. Rollup j 原来使用 calldata 就有很低的延迟成本，换到 blob 对其而言会带来更高的延迟成本，带来负面效果 i. Rollup j 原来选用 calldata 就能说明其更看重延迟成本 b. Rollup j 可以使用 blob 获得更低的数据均摊成本（不考虑延迟成本），带来正面效果 i. 非永久保存特性的 Blob 单字节成本原生低于永久保存的 Calldata ii. 按照当前的统计数据亦成立

场景 3：Rollup i 和 Rollup j 都采用 Calldata 作为数据可用方案

场景 3 中 Blob 的均衡价格会上升，最多为原来的 $3+2\sqrt{2}$ 倍

根据公式（22）可以得知未拼单时，Blob 的均衡价格 B 为

$$ \begin{equation} B=\frac{a(\sqrt{R_l}+...)^2}{2k^2} \end{equation} $$

• Rollup l 选择使用 Blob 发布可用性数据

Rollup i 和 Rollup j 联合发布 Blob 的均衡价格 $B_{joint}$ 可以表示为下列公式

$$ \begin{equation} B_{joint}=\frac{a(\sqrt{R_l}+\sqrt{R_i+R_j}+...)^2}{2k^2} \end{equation} $$

得到 B 和 $B_{joint}$ 的关系

$$ \begin{equation} (3+2\sqrt{2})B \ge (1+\sqrt{2k})^2\ge B_{joint} > B \end{equation} $$

证明

• $\sqrt{R_l}=\frac{1}{\sqrt{2}}\sqrt{R_l+R_l}\ge \frac{1}{\sqrt{2}}\sqrt{R_i+Rj}$ 得到 $(3+2\sqrt{2})B\ge B{joint}$。
  • $B_{joint}$ 在只有 Rollup l, Rollup i 和 Rollup j，且$R_l$等于 $R_i$ 等于$R_j$时，Blob 成本为原来的 $3+2\sqrt{2}$ 倍
• $\sqrt{R_i+Rj}>0$ 得到 $B{joint}>B$。

在场景 3 下采用拼单策略，由于 Rollup i 和 Rollup j 原来并不使用 Blob，因此拼单实际上会提高整体对 Blob 的需求，从而提高拼单后 Blob 的均衡价格。

场景 3 中拼单策略相对单独发布不一定是更优策略

根据公式（8）可以得到拼单后 Blob 的成本

$$ \begin{equation} cost{joint}=2B{joint} \end{equation} $$

根据公式（7）可以得到拼单后 Blob 中交易的数量

$$ \begin{equation} N{joint}=\sqrt{\frac{2B{joint}(R_i+R_j)}{a}} \end{equation} $$

根据公式（40）-（43）可以得到拼单前 Rollup i 和 Rollup j 若要发布拼单 Blob 内交易的成本

$$ \begin{equation} cost_i=cost^{calldata}i(N{joint}\frac{R_i}{R_i+R_j})=PbRi\sqrt{\frac{2B{joint}}{a(R_i+R_j)}} \end{equation} $$

$$ \begin{equation} cost_j=cost^{calldata}j(N{joint}\frac{R_j}{R_i+R_j})=PbRj\sqrt{\frac{2B{joint}}{a(R_i+R_j)}} \end{equation} $$

Rollup i 和 Rollup j 要发布拼单 Blob 内交易的成本

$$ \begin{equation} cost_{seperate}=cost_i+costj=Pb\sqrt{\frac{2B{joint}(R_i+R_j)}{a}} \end{equation} $$

Calldata 的成本对于使用 Blob 的 Rollup l 而言不如 Blob 划算，而对于使用 Calldata 的 Rollup i 和 Rollup j 而言比 Blob 划算。因此，根据公式（29），Pb 满足如下约束：

$$ \begin{equation} \sqrt{\frac{2Ba}{R_l}}\le Pb \le \sqrt{\frac{2Ba}{R_1}} \le \sqrt{\frac{2Ba}{R_2}} \end{equation} $$

根据公式（55）可以得到$cost_{seperate}$的范围约束

$$ \begin{equation} 2\sqrt{B_{joint}B}\sqrt{\frac{R_i+R_j}{Rl}}\le cost{seperate} \le 2\sqrt{B_{joint}B}\sqrt{1+f} \end{equation} $$

根据公式（49）可以进一步得到

$$ \begin{equation} 0< cost{seperate} \le 2\sqrt{B{joint}B}\sqrt{1+f}\le 2\sqrt{2}\sqrt{B{joint}B}\le2\sqrt{2}B{joint} \end{equation} $$

根据公式（38）以及（49）可以得知在场景二没有确定性的最优策略

• 当 $cost{seperate} \ge cost{joint}$，对于双方而言，拼单策略是最佳策略。
• 当 $cost{seperate} < cost{joint}$，对于双方而言，拼单策略非最佳策略。

💡 尝试直观地理解该结论。

1. Blob 的均衡价格上升，带来负面影响
2. Rollup i & j 切换到 blob，带来影响不能一概而论 a. Rollup i & j 原来使用 calldata 就有很低的延迟成本，换到 blob 对其而言会带来更高的延迟成本，带来负面效果 i. Rollup i & j 原来选用 calldata 就能说明其更看重延迟成本 b. Rollup i & j 可以使用 blob 获得更低的数据均摊成本（不考虑延迟成本），带来正面效果 i. 非永久保存特性的 Blob 单字节成本原生低于永久保存的 Calldata ii. 按照当前的统计数据亦成立

Blob 成本分摊

当 $cost{seperate} \ge cost{joint}$，对于双方而言，拼单是更优的策略，对应着

• 场景 1
• 部分场景 2
• 部分场景 3

Blob 的拼单策略意味着 Rollup 需要分摊各自的成本，这是典型的合作博弈的场景。纳什提出一种合作博弈的解决方法，该方法满足：

1. Invariant to affine transformations or Invariant to equivalent utility representations
2. Pareto optimality
3. Independence of irrelevant alternatives
4. Symmetry

纳什方法实际上就是求解 $B_i$，满足

$$ \begin{equation} \operatorname*{argmax}_{B_i}(Bi+cost^i{delay}-cost{i})((B{joint}-Bi)+cost^j{delay}-cost_{j}) \end{equation} $$

• $Bi+cost^i{delay}$为在拼单策略下 Rollup i 的成本
  • 前者为分摊的 Blob 成本
  • 后者为延迟成本
• $cost_i$为 Rollup i 单独发布的成本
• $(B_{joint}-Bi)+cost^j{delay}$为在拼单策略下 Rollup j 的成本
  • 前者为分摊的 Blob 成本
  • 后者为延迟成本
• $cost_j$为 Rollup j 单独发布的成本

公式（58）是一个关于 $B_i$的二次函数，容易得到 Rollup i 的最佳分摊成本

$$ \begin{equation} B{i}^{best}=\frac{B{joint}+((cost_i-costj)-(cost^{i}{delay}-cost^j_{delay}))}{2} \end{equation} $$

💡 两个 rollup 拼单实际上可以推广成 n 个 rollup 拼单，结论类似。若是 3 个 Rollup 进行拼单，实际上只需在（58）新增一个乘积项即可，如此类推

场景 1 应该是最贴近现实的场景，下面的推导会聚焦在场景 1。另外，由于在场景 2 和 3 中，不一定采用拼单策略，涉及因素过多（如 P, b 的取值），难以洞察一些分摊性质。

在场景 1 中，求解 $B^{best}_i$

$$ \begin{equation} B^{best}{i}=B{joint}\frac{f}{1+f}+\sqrt{B_{joint}B}\frac{1-\sqrt{f}}{\sqrt{1+f}} \end{equation} $$

性质 1：必然存在最佳成本均摊方案

上述性质可以表述为 $B^{best}i\le B{joint}$

证明：根据公式（25）可以得到

$$ \begin{equation} B^{best}{i}\le B{joint}\frac{f}{1+f}+B{joint}\frac{1+\sqrt{f}}{\sqrt{1+f}}\frac{1-\sqrt{f}}{\sqrt{1+f}}=\frac{B{joint}}{1+f}\le B_{joint} \end{equation} $$

💡 该性质实际上是很直观。因为场景 1 中拼单策略是更优的策略，因此一定存在合法的 $B^{best}_i$，不会让参与者分配到负值的情况。反观，场景 2 和场景 3 不一定存在合法值。

性质 2：大型 Rollup 需要支付低于其交易比例的 Blob 费用

上述性质可以表述为 $B^{best}_i\le \frac{R_i}{R_i+Rj}B{joint}=\frac{B_{joint}}{1+f}$

证明：根据公式（61）可以得到直接达到。

该性质实际上是很直观。因为小型 Rollup 相对于大型 Rollup 在 Blob 的联合发布上有着更大的需求和更多的获益，理应分摊更多的成本，即高于其数据比例。

性质 3：大型 Rollup 需要支付超过一半的 Blob 费用

上述性质可以表述为 $B^{best}i\ge \frac{B{joint}}{2}$

证明：

等价于证明

$$ \begin{equation} \frac{B_{joint}}{B}\le\frac{4(1+f)}{(1+\sqrt{f})^2} \end{equation} $$

根据公式（25）可以得知，只需要证明

$$ \begin{equation} \frac{4(1+f)}{(1+\sqrt{f})^2}\ge 1 \end{equation} $$

公式（63）左侧是一个单调递减函数，因此 f 取 1 到达其最小值 1，得证。

💡 该性质实际上是很直观。大型 Rollup 虽然可以支付低于其交易比例的费用，但是其支付必须比小型 Rollup 多。否则，小型 Rollup 的交易比大型 Rollup 的交易少，反而要支付得比大型 Rollup 要多，这是不符合常理的。

综合性质 2 和性质 3 可以得到

$$ \begin{equation} \frac{B_{joint}}{1+f} \ge B^{best}i\ge \frac{B{joint}}{2} \end{equation} $$

性质 4：小型 Rollup 单笔交易成本优化效果更佳

Rollup i 在 Blob 的交易数量为

$$ \begin{equation} N_i=Ri\sqrt{\frac{2B{joint}}{a(R_i+R_j)}} \end{equation} $$

Rollup j 在 Blob 的交易数量为

$$ \begin{equation} N_j=Rj\sqrt{\frac{2B{joint}}{a(R_i+R_j)}} \end{equation} $$

Rollup i 的平均交易成本为

$$ \begin{equation} cost^i_{avg}=\frac{B^{best}_i+cost^{delay}_i}{N_i} \end{equation} $$

Rollup j 的平均交易成本为

$$ \begin{equation} cost^j{avg}=\frac{B{joint}-B^{best}_i+cost^{delay}_j}{N_j} \end{equation} $$

根据公式（29）对于 Rollup i 而言，其单笔交易成本的优化率为

$$ \begin{equation} q_i=\frac{cost^{blob}i-cost^i{avg}}{cost^{blob}_i} \end{equation} $$

根据公式（29）对于 Rollup j 而言，其单笔交易成本的优化率为

$$ \begin{equation} q_j=\frac{cost^{blob}j-cost^j{avg}}{cost^{blob}_j} \end{equation} $$

具有性质 $q_i\le q_j$

证明

等价于证明

$$ \begin{equation} \frac{2}{1+f}+\sqrt{\frac{B}{B_{joint}}}\frac{1-f}{\sqrt{1+f}}-\sqrt{f}\ge0 \end{equation} $$

显然公式（71）的左侧是一个关于 f 的单调递减函数，因此当 f=1 时取得最小值 0，得证。

💡 该性质实际上是很直观。拼单策略对于小型 Rollup 而言大大降低其延迟成本，降低程度远大于大型 Rollup，而大型 Rollup 的延迟成本可能本来就不算高。

后记

EIP-4844 下 Rollup 数据可用策略让我们辩证地看待新旧技术，每种不同的技术都有其适用的范围，我们需要划清各个技术的效用边界，从而让我们更有效率地利用技术。延迟成本基本主导了本文的推导，而这块在平时的讨论中都隐藏在水下。

后续仍有很多开放的研究空间，如限制 Calldata 的 EIP 敲定后，Rollup 数据可用策略会发生什么变化。欢迎加入 ETHconomics Research Space 一起讨论研究。

相关资料

EIP 4844: What does it mean for L2 users?

https://medium.com/offchainlabs/eip-4844-what-does-it-mean-for-l2-users-5e86ebc4c028

EIP-4844 Economics and Rollup Strategies

https://arxiv.org/abs/2310.01155