比特币技术原理与应用-2 数据结构
- 符钦伟
- 发布于 2020-04-04 11:14
- 阅读 8493
比特币中使用哈希指针保存前一个区块头的哈希值,将多个区块连接成一条链,保证了区块链的不可篡改特性。比特币还使用梅克尔树保存区块体中的交易数据,从最底层的交易数据通过哈希指针层层传递到根哈希,浓缩了所有的交易数据,提高了篡改交易的难度。梅克尔树还提供交易数据隶属证明和非隶属证明的高效方法,时间复杂度均为O(log N)。
本系列文章: 比特币技术原理与应用-1 密码学基础 比特币技术原理与应用-2 数据结构
2天前 发表了文章
比特币技术原理与应用-1 密码学基础
哈希指针H( )
比特币中通过哈希指针将多个区块连接成一条链。 在本质上,区块链也是一个链表,只不过用哈希指针代替了普通指针。
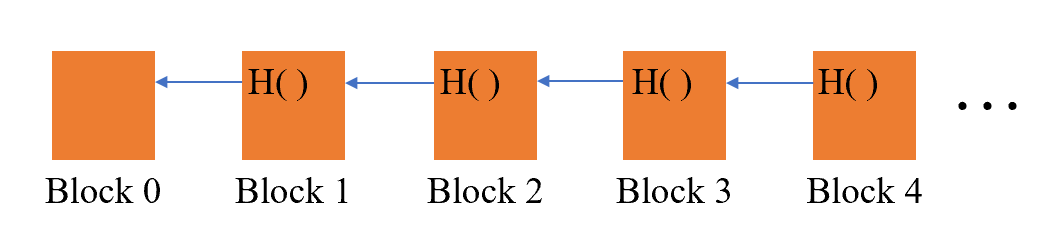
为了说明哈希指针的优点,我们先了解一下单向链表(singly-linked list)和普通指针。
以C++为例,单向链表中的节点通常是结构体数据类型,包含节点的值val和指向下一个节点的指针next。
//单向链表节点 结构体,包含节点的值val和指向下一个节点的指针next
struct ListNode {
int val;
ListNode *next;
ListNode(int x) : val(x), next(NULL) {}
};Node 0又称为根节点(root node),根节点是链表的初始节点,没有指向任何节点,因此根节点的next指针为空(Node 0.next = NULL)。Node 1中的next指针存储了Node 0的地址(Node 1. next = Node 0_address),指向Node 0。同理,Node 2指向Node1, Node 3指向Node 2... 如果要往链表中加入新节点,只需要新建一个节点,并将新节点的next指针指向链表的末尾节点。链表相比于数组的优势是什么?链表的可扩展性更强,一个数组中的元素在磁盘上是先申请一块空间然后连续存储的,而链表中的节点元素可以存储在不同的磁盘位置,通过指针存储下一个节点的地址,然后去磁盘上寻址找到下一个节点。如果要修改链表中的某个节点的值,我们可以寻址找到该节点,并修改节点的值val即可。

在使用普通指针的单向链表中,我们可以随意修改任意节点的值val,而不会破坏链表的完整性。如果比特币也采用普通指针连接成一个普通链表,那我们就可以任意修改区块中的交易信息,这就破坏了区块链的不可篡改特性(严格来说,是难以篡改)。相比于普通指针,哈希指针不仅能把区块连接成一条链,还能保证区块不可篡改。
一个区块(Block)的结构,包含区块头(Block Header)和区块体(Block Body),下图简单列举了Block Header和Block Body中包含的数据信息,区块结构的具体内容我将在系列博客3-比特币协议中详细讲解。

哈希指针H( )是对上一个区块的Block Header取哈希值,Block Header中的Merkle Tree哈希值已经包含了Block Body的信息,这也是为什么只需要对Block Header 取哈希的原因,减少了哈希函数的输入数据大小从而提高哈希运算的速度。Block 0又称为创世区块(genesis block),Block 1中的H()为Block 0 header的哈希值,Block 2中的H()为Block 1 header的哈希值······ 如果有新区块要加进来,只需把最末尾区块的header哈希值计算出来,放在新区块的header中即可,这样就连接成了一条区块链。
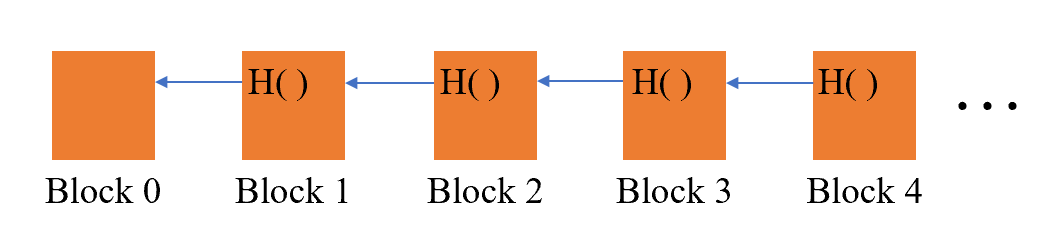
哈希指针提高了篡改的难度,防止篡改区块中的数据。 假设我修改了Block 1中的数据,那么根据哈希函数的碰撞阻力特性,Block 1 header的哈希值发生变化,那么我就要修改Block 2 header中的哈希指针,Block 2 header发生变化,同理我也需要修改Block 3 header······ 相当于一个连锁反映,篡改区块链中的某个区块,就需要篡改该区块之后的所有区块,大大提高了篡改区块的难度。
Merkle Tree(梅克尔树)
Block body中存储交易信息的数据结构就是Merkle Tree。Merkle Tree根哈希反映了所有的交易信息,修改任意一个交易数据都会造成根哈希的变化,防止篡改交易数据,并且能够快速验证某笔交易属于这个区块(隶属证明)或者不属于这个区块(非隶属证明)。
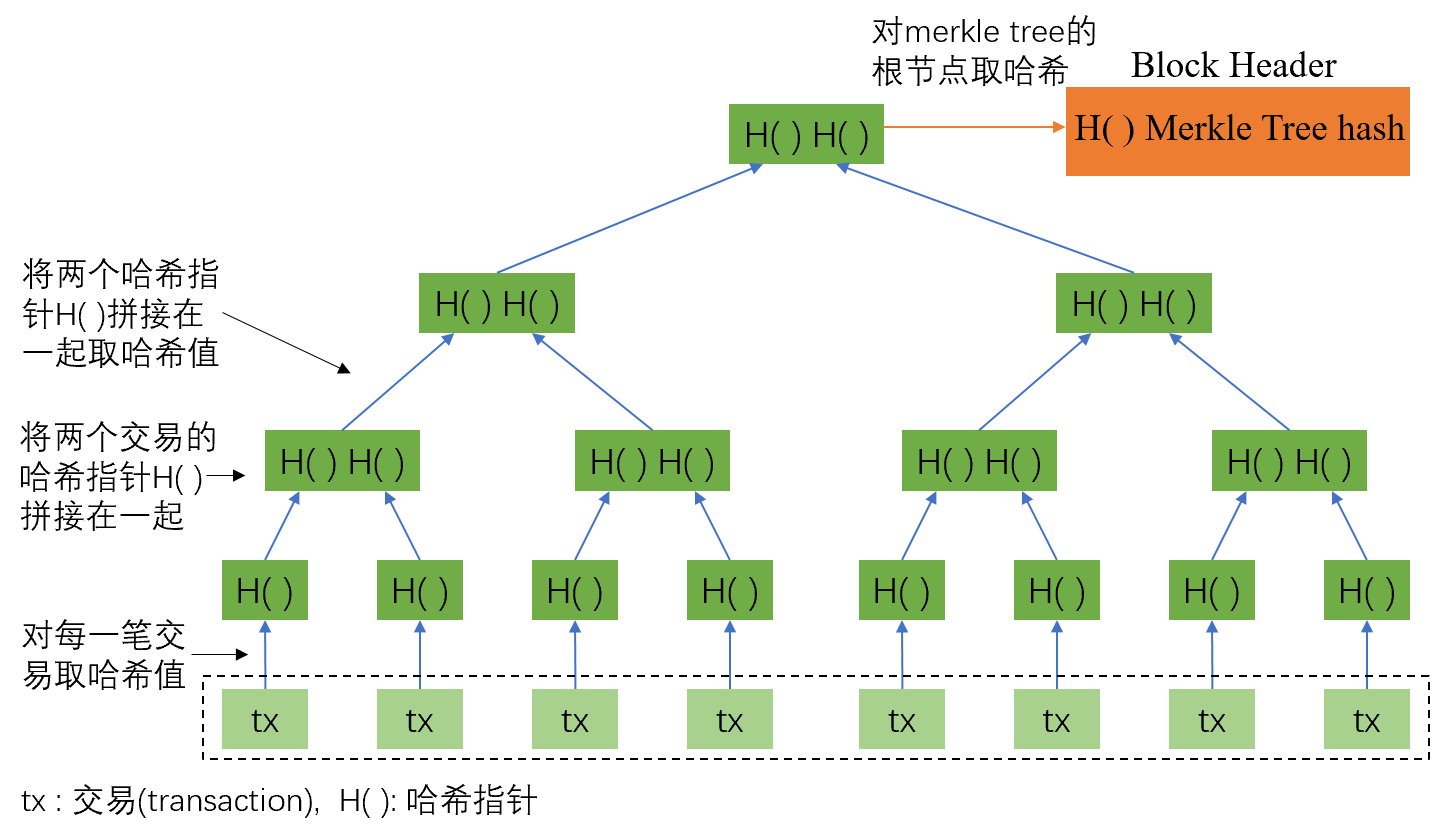
相比于普通的二叉树,Merkle Tree采用了哈希指针代替普通指针,提高了篡改交易的难度。Merkle Tree的最底层叶子节点存的是交易信息,对每一笔交易取哈希值得到H( ),两个相邻的H()拼接在一起作为两个相邻哈希指针节点的父节点,依次迭代,最终得到Merkle Tree的根节点。根节点也是由两个子节点的哈希值拼接在一起的,根节点相当于包含了所有的交易信息,假设任意一笔交易信息变化,都会层层传递导致根节点的变化。最终,对Merkle Tree的根节点取哈希值,存在区块头的Merkle Tree Hash字段中,从而保证区块头包含了所有的交易信息,任意一笔交易信息变化层层传递导致区块头的变化,该区块头的变化又会导致区块头取哈希值的变化,块块传递导致该区块之后每一个区块发生变化,提高了篡改交易信息的难度。
查找一笔交易是否属于Merkle Tree,验证一笔交易属于Merkle Tree称为隶属证明,反之成为非隶属证明。
隶属证明
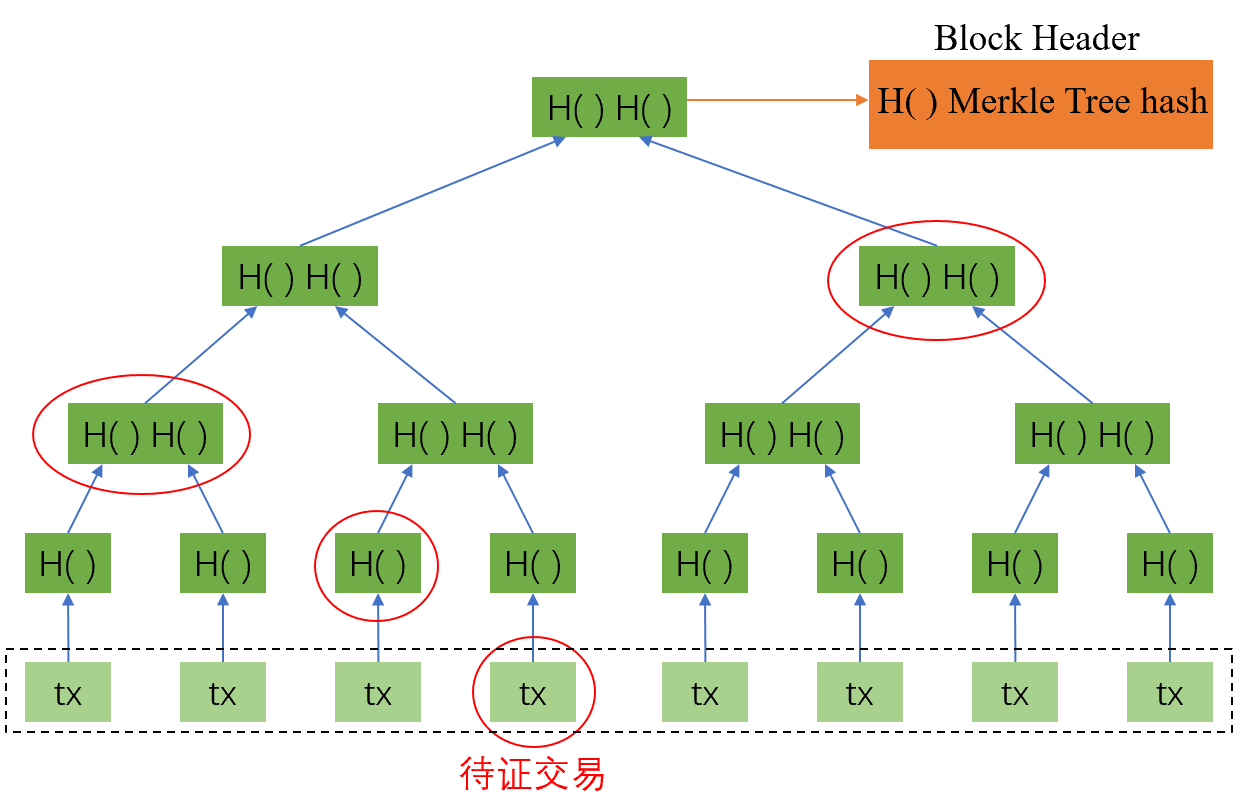
下图中,假设我们需要验证一笔待证交易存在Merkle Tree中,只需要提供部分节点信息(下图中红圈部分),经过自底向上的哈希运算后,最终算出Merkle Tree hash。我们将哈希运算结果与该区块头中的Merkle Tree hash作比较,如果相等则证明了待证交易确实存在这个Merkle Tree中。
使用Merkle Tree做交易的隶属证明,假设包含N笔交易,Merkle Tree的高度为O(log N)+1,则验证一笔交易的时间复杂度为O(log N)。
非隶属证明
如何证明一笔交易不属于Merkle Tree?方法是使用排序梅克尔树(sorted Merkle Tree),相比于Merkle Tree,sorted Merkle Tree中最底层的交易数据是有序排列的。先假设待证交易X在Tree中,根据有序排列的交易数据可以推算出排在待证交易之前的交易A和排在待证交易之后的交易B,如果我们使用隶属证明中的方法证明了交易A和B都隶属于sorted Merkle Tree且交易A和B是相邻紧挨着的(时间复杂度为O(log N)),那么意味着在树中A和B之间是没有空间放下待证交易X的,从而证明了待证交易X不隶属于Merkle Tree。
小结
比特币中使用哈希指针保存前一个区块头的哈希值,将多个区块连接成一条链,保证了区块链的不可篡改特性。比特币还使用梅克尔树保存区块体中的交易数据,从最底层的交易数据通过哈希指针层层传递到根哈希,浓缩了所有的交易数据,提高了篡改交易的难度。梅克尔树还提供交易数据隶属证明和非隶属证明的高效方法,时间复杂度均为O(log N)。
参考文献:
- 北京大学肖臻老师《区块链技术与应用》公开课
- 《区块链 技术驱动金融:数字货币与智能合约技术》[美] 阿尔文德·纳拉亚南(Arvind Narayanan),约什·贝努 等 著,林华,王勇,帅初 等 译
- ZKPassport:我们现在在哪里? 1609 浏览
- PoRv2:一种快速、透明的基于 ZK 的储备证明 1466 浏览
- 隐私货币:第三部分 2097 浏览
- Solana 上的压缩 NFT 1169 浏览
- ZKStack跨链架构内幕 — 第二部分:网关结算和递归证明 368 浏览
- 有状态哈希还是无状态哈希——这是后量子问题 1848 浏览
- ZKStack 跨链架构内幕 — 第一部分:Merkle 树层级结构的深度解析 1649 浏览
- ZKStack 跨链架构内幕 — 第一部分:Merkle 树层级结构的深度解析 2467 浏览
- 深入探讨Binius M3算术化,以Merkle树包含为例 1519 浏览
- 网络安全基石的奠基人:Ralph C Merkle 1617 浏览
- 区块链的分类与适用场景 5214 浏览
- 区块链的基本原理与特征 8594 浏览

