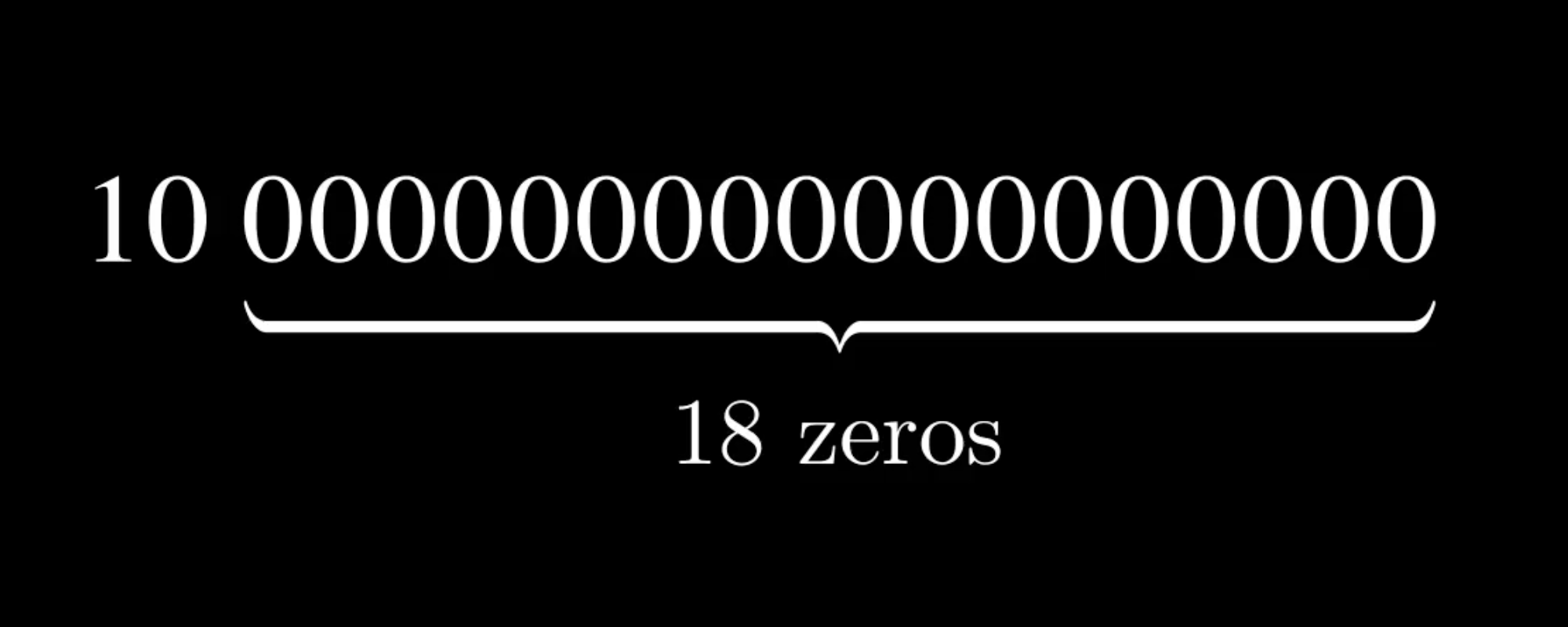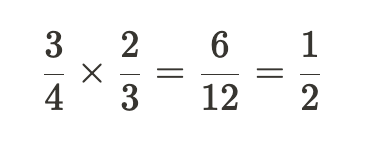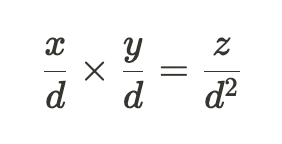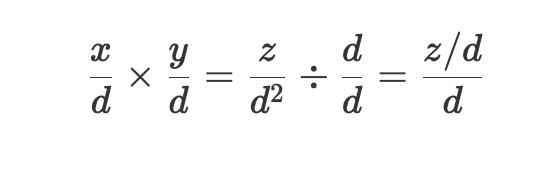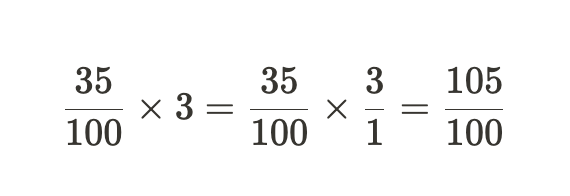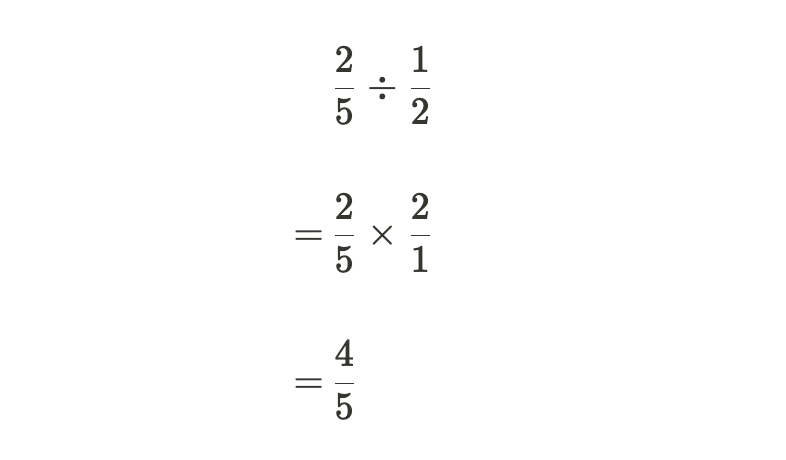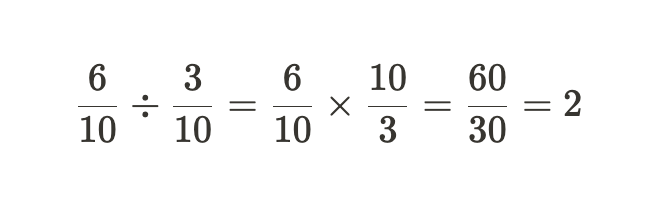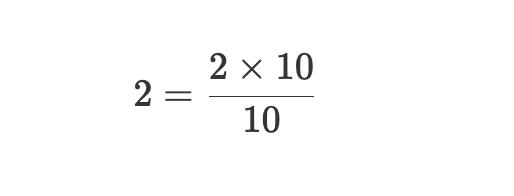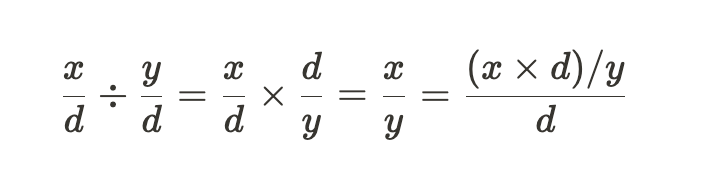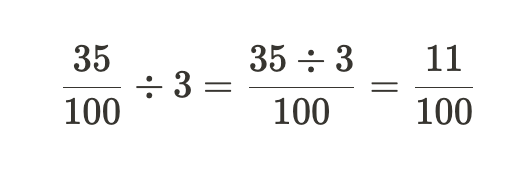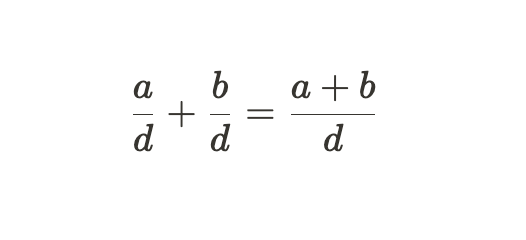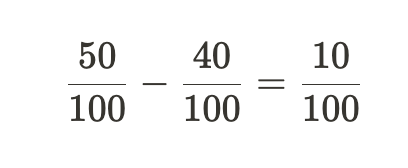Solidity 中的定点数运算(以 Solady、Solmate 和 ABDK 为例)
- RareSkills
- 发布于 2024-06-21 17:59
- 阅读 3528
定点数是一个仅存储分子部分的整数——而分母是隐含的。
定点数是一个仅存储分子部分的整数——而分母是隐含的。
在大多数编程语言中,这种类型的算术运算是不必要的,因为它们有浮点数。在 Solidity 中则是必要的,因为 Solidity 只有整数,而我们经常需要进行分数运算。
定点数在大多数 DeFi 智能合约中都能找到,因此理解它们是必须的。
例如,如果“隐含分母”是 100,那么持有“10”的定点数被解释为 0.1。
Solidity 中最常见的定点数是 10¹⁸:这是以太坊和大多数 ERC-20 代币的“小数位数”。当我们读取以太坊地址的余额时,我们隐含地将数字除以 10¹⁸ 来确定它们的以太币数量。例如,一个地址的余额为 10¹⁹ 被解释为拥有 10 个以太币——因为隐含地除以 10¹⁸。
具有 10¹⁸ 分母的定点数如此常见,以至于 Solidity 社区的工程师称之为“Wad”(这个名字最早由 MakerDAO 引入)。有时,一个 18 位的定点数被解释为最右边的 18 位分配给小数位,例如,数字“10”如下所示:
然而,我们发现这种心智模型使得理解固定点算术变得更难,因此本文将使用定点数持有分子,隐含 10¹⁸ 分母的心智模型。
在本文中,我们将学习如何使用定点数进行算术运算,并解释流行的固定点库如何工作。
将整数转换为定点数
要将整数转换为定点数,将整数乘以隐含分母。例如,“2 ether”是 2 × 10¹⁸,因此将整数 2 转换为“2 ether”我们将其乘以 10¹⁸。隐含的 10¹⁸ 分母抵消了 10¹⁸。
定点数的乘法
要将两个定点数相乘,我们遵循分数相乘的规则:
-
将分子相乘
-
将分母相乘
-
简化结果。
例如:
然而,在实际操作中我们可以优化这个计算,因为定点数的分母总是相同的。
现在让我们考虑一组具有共同分母的分数:
然而,我们不希望返回一个隐含分母为𝑑的结果,因为这与我们选择的隐含分母不兼容。因此,我们需要将分子和分母除以𝑑,以返回一个与我们选择的分母一致的定点数。
因此,如果 𝑥 和 𝑦 是隐含分母为 𝑑² 的定点数,我们可以将它们的乘积计算为 (𝑥 × 𝑦)/𝑑。
定点数乘法的代码示例
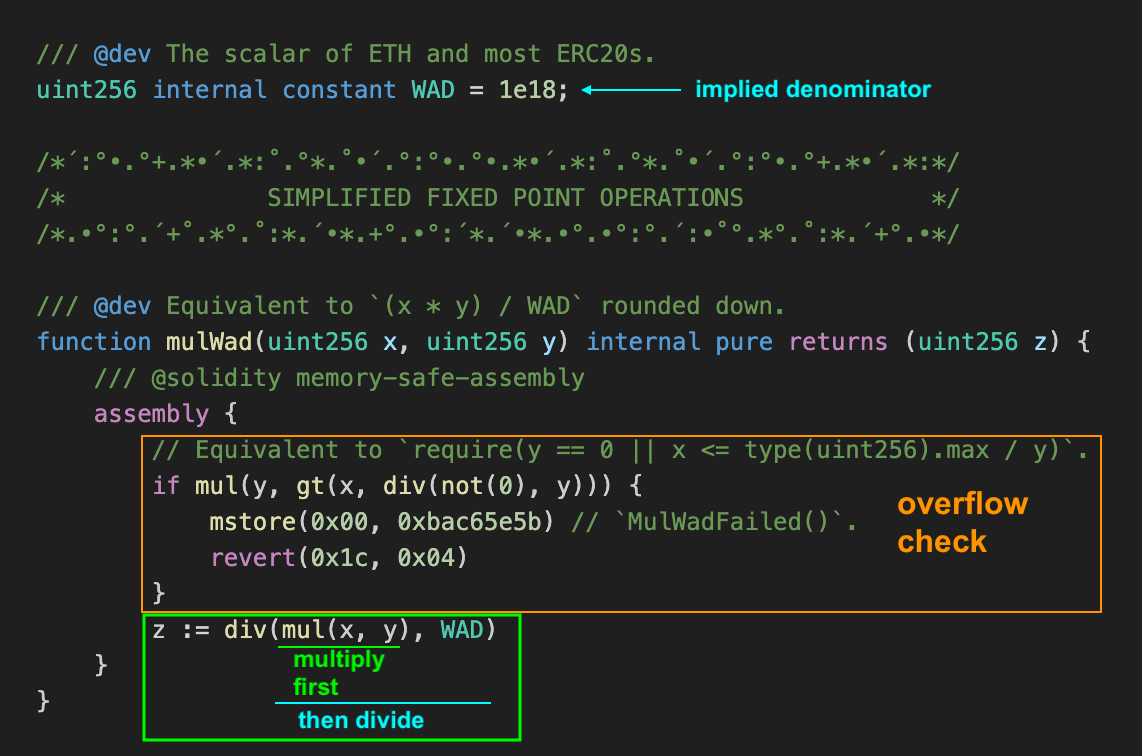
Solady 库有一个mulWad数学操作,用于将两个隐含 Wad 分母(10¹⁸)的定点数相乘。下面,我们展示代码并解释它如何与我们之前的讨论相关:
核心算法在截图底部(绿色框内)。我们在那里计算 (𝑥 × 𝑦)/𝑑,其中 𝑑 是WAD或 10¹⁸(如截图顶部所示,WAD被声明)。
现实世界的例子
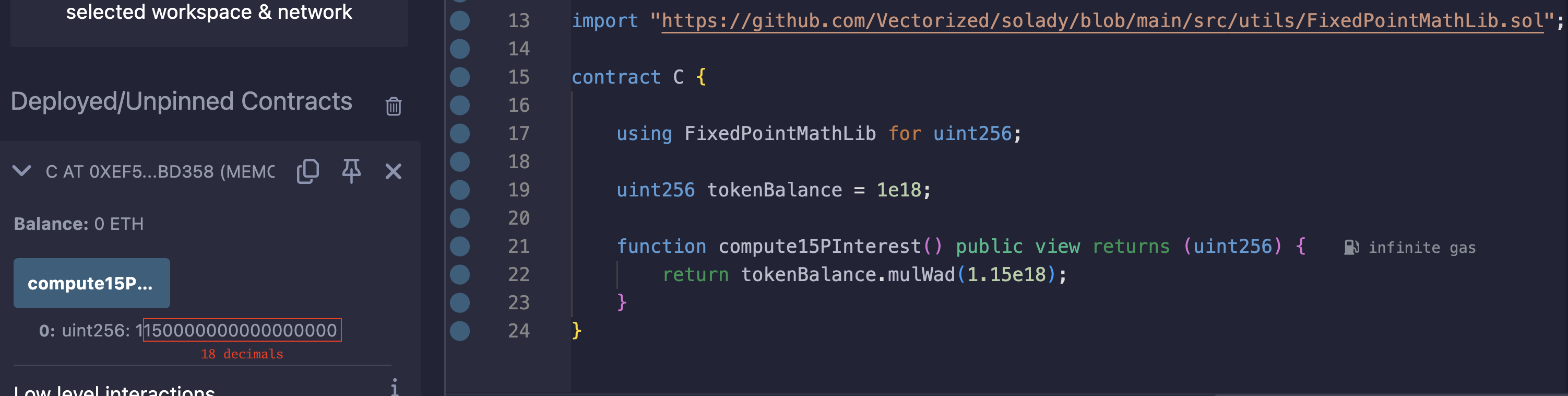
假设一个用户有 1 DAI(具有 18 个小数位),我们希望计算他们的余额,假设他们的存款赚取了 15%的利息。这是一个需要固定点算术的明确例子,因为我们不能在 Solidity 中直接将一个数字乘以 1.15。
输出是 1.15,在除以 1e18 之后。当然,我们不能实际除以 1e18,因为那样会抹去小数位。我们需要一个固定点表示,因为 1.15 不能表示为整数。上面的代码可以在 Remix 上测试 。
将定点数乘以整数
将分数 x 乘以整数 y 与将 x 乘以 y/1 相同:
因此,当我们将定点数乘以整数时,我们不需要任何额外步骤。我们只需将返回值解释为分母不变的定点数。
定点数的除法
要将分数相除,我们“翻转”第二个分数并将它们相乘。例如:
现在让我们考虑一个具有相同分母的例子:
注意,公共分母 10 被抵消了。如果我们想用隐含分母 10(即具有分母 10 的定点数)表示 2,我们需要再次将其乘以 10:
因此,对于具有公共分母 𝑑 的一般 𝑥 和 𝑦,如果我们想用隐含分母 𝑑 表示输出,我们必须执行以下操作:
因此,如果 𝑥 和 𝑦 是隐含分母为𝑑的定点数,我们可以将它们的商计算为 (𝑥 × 𝑑)/𝑦。
如果我们将mulWad()和divWad()并排放置,我们可以看到它们之间的唯一区别(在计算步骤,而不是溢出检查),是 div 情况乘以一个倒数分数。
将定点数除以整数
假设我们想将 2.5 除以 2(或一般情况下将某个分数除以整数)。不需要通过 (2 × 𝑑)/𝑑将 2 转换为定点数。
将分数 x 除以整数 y 与将 x 的分子除以 y 是一样的。
注意 35 ÷ 3 = 11,而不是 11.666,因为我们使用的是整数除法,而不是浮点数。我们只需将定点数除以整数,并将结果解释为定点数。与将定点数乘以整数一样,分母保持不变。
加减定点数
具有相同分母的分数相加减时,只需将分子相加减,分母忽略不计。我们将和解释为具有与加数相同隐含分母的定点数。例如,
因此,当相加具有相同分母的定点数时,我们只需像处理普通整数一样将这些数相加。
考虑一个隐含分母为 100 的例子:
计算时,我们只需做 50 - 40 = 10,不需要将 100 纳入计算。
二进制与十进制定点数
二进制定点数是分母可以表示为 2ⁿ 的定点数。二进制定点数通常用 Q 表示法表示。例如,UQ112x112 使用 2¹¹² 作为分母。U 表示“无符号”。用于存储 UQ112x112 的数据类型是 224。另一种解释方式是“小数部分”存储在最右边的 112 位,“整数部分”存储在最左边的 112 位。
另一个例子,UQ64x64(或 UQ64.64)是一个uint128,其中“小数部分”存储在最低有效的 64 位,“整数部分”存储在最高有效的 64 位。这仍然可以解释为具有隐含分母 2⁶⁴,如下所示。
二进制定点数的优点是我们可以使用 gas 高效的左移位操作代替乘以分母(当将整数转换为定点数时),或在除法时使用右移位操作。
作为一个基本例子,考虑以下情况: (1) 2 的二进制表示是 10 (2) 16 的二进制表示是 10000 (3) 16 = 2 × 2³ (4) binary(1000) = binary(10) << 3
注意在(3)中 3 是指数,在(4)中是我们左移位的位数。
位移操作与乘以 2ᵉ之间的关系通常成立。以下操作是等效的:
// x \* 2¹¹² 等于 x 左移 112 位
x \* 2 \*\* 112 == x << 112
// x / 2¹¹² 等于 x 右移 112 位
x / 2 \*\* 112 == x >> 112x 可以是任意数字,只要它适合无符号整数。
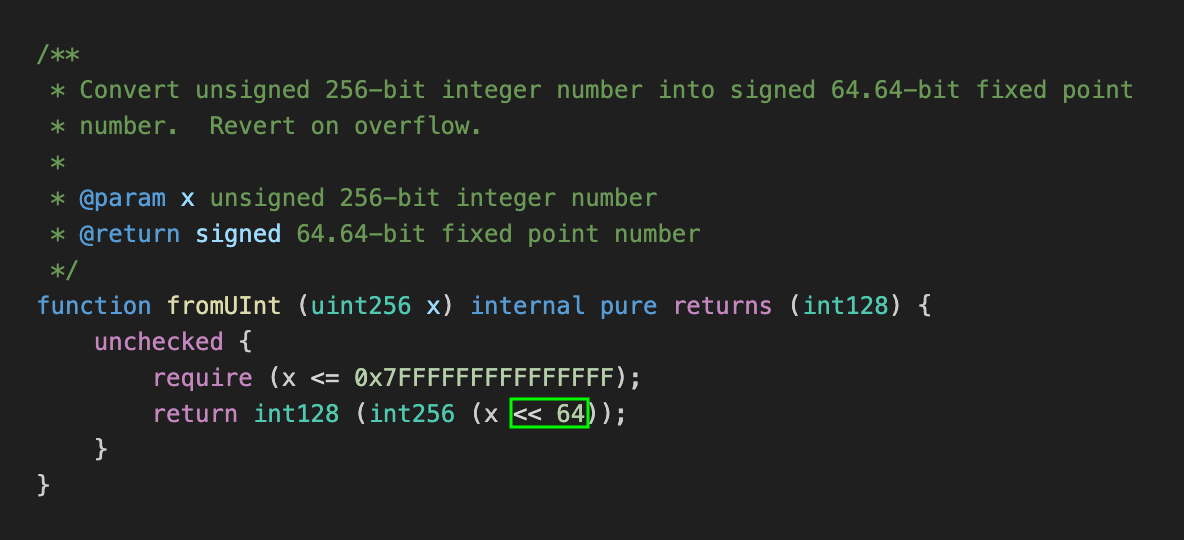
ABDK 库使用以下函数将无符号整数转换为定点数(隐含分母为 2⁶⁴):
require 语句确保 x 小于type(int64).max,因为 ABDK 库使用有符号定点数。左移 64 位相当于乘以 2⁶⁴。
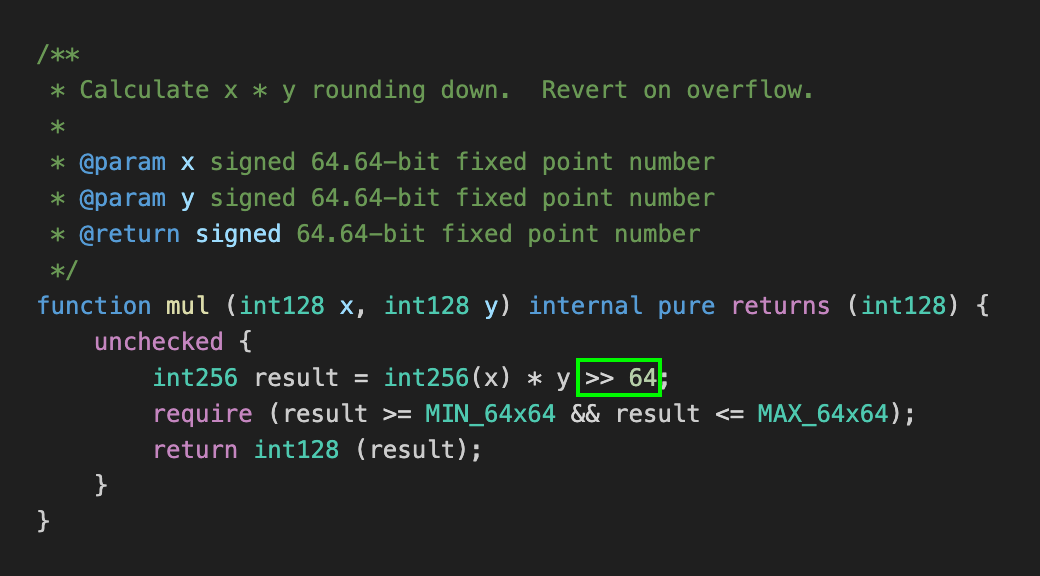
类似地,当 ABDK 进行乘法运算时,它不是将 x 和 y 的乘积除以 2⁶⁴,而是右移 64 位:
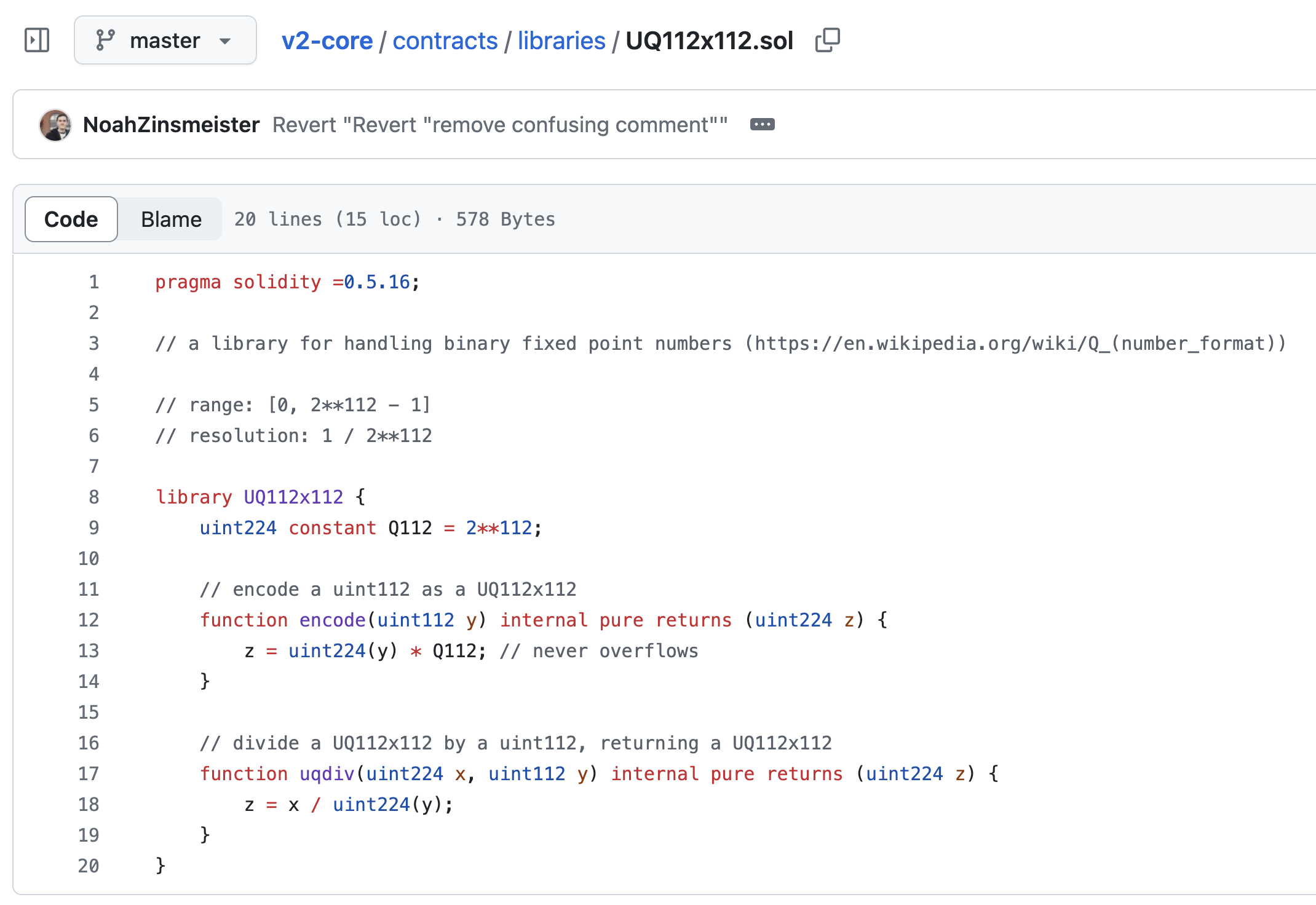
Uniswap V2 定点数库
Uniswap V2的定点数库非常简单,因为 Uniswap V2 对定点数的唯一操作是加法和将定点数除以整数。
encode()函数将一个uint112转换为存储在uint224中的定点数。Uniswap V2 使用隐含分母2**112。如果使用位移操作代替乘法,它可能会更节省 gas(这可能是 Uniswap 开发者的一个错误)。
定点数存储在一个uint224中,其大小是与之交互的uint112的两倍。在编码操作期间,uint112数字的位实际上被移到uint224的最高有效 112 位。
这种“编码”操作在较小的 uint 大小下更容易可视化。让我们使用一个假设的分母为 2⁸ 的定点数。下面,我们展示了将一个uint8编码为分母为 2⁸ 的定点数时发生的情况:
从数字 125 开始,其二进制表示为01111101,如果将其乘以 2⁸,乘积为 32000,当存储在 16 位 uint 中时表示为0111110100000000。注意,将 125 乘以 2⁸与左移 8 位效果相同。
uqdiv()函数只是将定点数除以整数,不需要额外步骤。
Uniswap 使用这个库来累积 TWAP Oracle 的价格。每次更新发生时,TWAP 将最新价格添加到累加器中(累加器用于计算平均价格,涉及额外步骤,不在本文范围内)。由于价格表示为分数,定点数是表示它们的理想方式。
变量_reserve0和_reserve1保存池的最新代币余额,类型为 uint112。price0CumulativeLast和price1CumulativeLast是 UQ112x112(隐含分母为 2¹¹² 的定点数)。下面的 Uniswap V2 代码将分子转换为定点数(UQ112x112)并将其除以整数(分母未转换为 UQ112x112)。结果是一个定点数。
向上取整与向下取整
定点数库通常有在除法时向上取整的选项。例如,Solady 有:
-
mulWadUp— 乘以两个定点数,但在除以 d 时向上取整。回想一下,乘以两个定点数的公式是(x × y) / d。 -
mulDivUp— 除以两个定点数,但在除法时向上取整
Solidity 除法总是向下取整,例如 10 / 3 = 3。然而,如果我们向上取整,10 / 3 将等于 4。当计算信用或价格时,应始终向协议有利、用户不利的方向取整。例如,如果我们在计算用户应支付的另一种资产的固定金额,我们应向上取整价格。
-
10 / 3 向下取整是 3.3333
-
10 / 3 向上取整是 3.3334(取决于我们的分母大小)
向上取整简单来说就是如果余数不为零,则在结果上加 1。例如,9 / 3 = 3 正好,所以我们不应该返回 4。然而,10 / 3 和 11 / 3 的余数分别是 1 和 2,所以我们应该在除法结果上加 1。
在绿色下划线部分,代码检查模数是否大于零。如果是,则在结果上加 1(向上取整),否则加 0(不取整)。
本文由 AI 翻译,欢迎小伙伴们来校对。
- 翻译
- 学分: 9
- 分类: Solidity
- 标签: Solidity Solidity 数学运算
- 深度拆解 Grass 模式:基于 EIP-712 与 DePIN 架构的奖励分发系统实现 20 浏览
- 2026 年智能合约审计的实际成本 75 浏览
- 深度解构:如何利用 Solidity 0.8.24 与 AI 代理复刻现象级 Pi Network 生态 95 浏览
- 深度实战:使用 Solidity 0.8.24 + OpenZeppelin V5 实现 Pepe 与 Dogecoin 的核心逻辑 96 浏览
- 深度解析|Form Network:BNX 迁移模块化 L2 的全流程技术实践 152 浏览
- STEPN相关内容延续篇:基于OpenZeppelinV5与Solidity0.8.24的创新点拆解 201 浏览