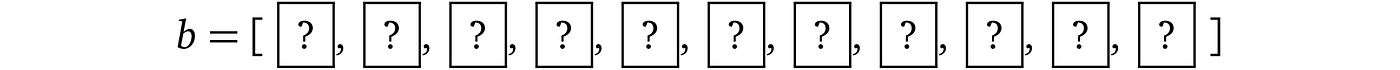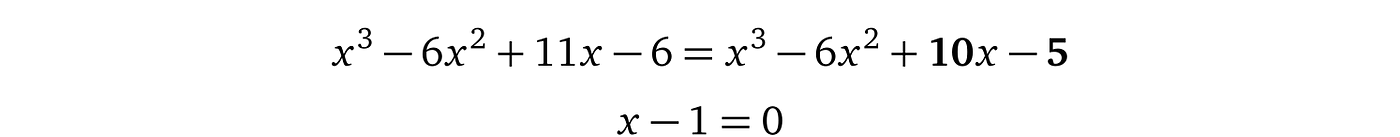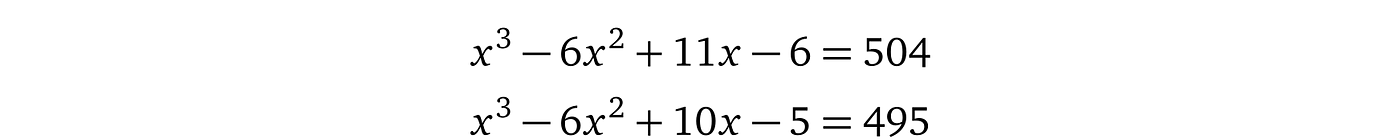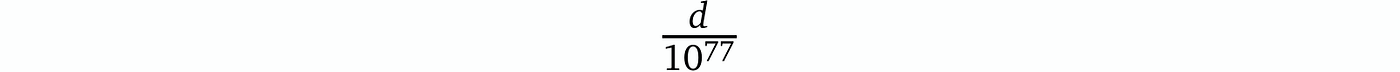• 原文链接：https://medium.com/@imolfar/why-and-how-zk-snark-works-1-introduction-the-medium-of-a-proof-d946e931160
• 译者：AI翻译官，校对：翻译小组
• 本文永久链接：learnblockchain.cn/article…

为什么和如何 zk-SNARK 工作 1：介绍与证明的媒介

本文是 PDF 版本的改编.

尽管关于 zk-SNARK 构造的资源很多，从原始论文 [Bit+11; Par+13] 到解释文章 [Rei16; But16; But17; Gab17]，由于涉及的部分众多，这个主题对许多人来说仍然是一个黑箱。虽然提供了一些拼图，但没有缺失的部分就无法看到完整的图景。

作者第一次发现这些部分如何完美契合时，被数学的美丽所震撼，随着更多维度的揭示，这种惊奇感不断增强。因此，本工作的重点是通过基于示例的直接和清晰的方法来分享这一经验，并在此过程中回答许多为什么，以便更多的人能够欣赏这项尖端技术、其创新者以及最终的数学之美。

本工作的贡献是以足够的复杂性进行简化的阐述，必要的复杂性足以理解 zk-SNARK，无需任何先决知识、密码学或高级数学。主要目标不仅是解释它如何工作，还要解释它为什么工作以及它是如何形成的。

前言

虽然最初计划简短，但现在工作已经扩展到几十页，然而它需要的先决知识非常少，可以自由跳过熟悉的部分。

如果你不熟悉一些使用的数学符号，不必担心，这些符号很少，并且会逐步引入，一次一个。

介绍

零知识 简洁非交互知识论证 (zk-SNARK) 是一种真正巧妙的方法，可以在不透露任何其他信息的情况下证明某事是真实的，然而，为什么它首先有用呢？

零知识证明 在许多应用中具有优势，包括：

1) 证明私人数据的声明：

• 人 A 的银行账户中有超过 X
• 去年，某银行没有与实体 Y 进行交易
• 匹配 DNA 而不透露完整的 DNA
• 某人的信用评分高于 Z

2) 匿名授权：

• 证明请求者 R 有权访问网站的受限区域而不透露其身份（例如，登录名、密码）
• 证明某人来自允许的国家/州列表而不透露具体来自哪个国家/州
• 证明某人拥有地铁/地铁的月票而不透露卡的 ID

3) 匿名支付：

• 完全脱离任何身份的支付 [Ben+14]
• 在不透露收入的情况下缴税

4) 外包计算：

• 外包昂贵的计算并验证结果是否正确而不重新执行；它开启了一个无信任计算的类别
• 将区块链模型从每个人都计算相同的内容更改为一个人计算，所有人验证

尽管表面上听起来很棒，但其底层方法是数学和密码学的“奇迹”，自 1985 年在主要工作“交互式证明系统的知识复杂性” [GMR85] 中引入以来，已经研究了四个十年，随后引入了非交互式证明 [BFM88]，这在区块链的背景下尤为重要。

在任何 零知识证明 系统中，有一个 证明者 想要说服一个 验证者 某个 声明 是真实的而不透露任何其他信息，例如，验证者 了解到 证明者 的银行账户中有超过 X，但没有其他信息（即实际金额未披露）。协议应满足三个属性：

• 完整性 — 如果 声明 是真实的，那么 证明者 可以说服 验证者
• 可靠性 — 欺骗的 证明者 不能说服 验证者 一个虚假的 声明
• 零知识 — 交互只揭示 声明 是否真实，其他任何信息都不透露

zk-SNARK 术语本身在 [Bit+11] 中引入，基于 [Gro10]，随后是 Pinocchio 协议 [Gen+12; Par+13]，使其适用于通用计算。

证明的媒介

让我们从简单的开始，尝试证明一些东西，而不考虑零知识、非交互性、其形式和适用性。

假设我们有一个长度为 10 的位数组，我们想向验证者（例如程序）证明所有这些位都设置为 1。

验证者只能一次检查（即读取）一个元素。为了验证声明，可以通过以某种任意顺序读取元素并检查它是否确实等于 1 来进行，如果是，则对该声明的信心在第一次检查后为 ⅒= 10%，或者如果该位等于 0，则声明完全无效。验证者必须继续下一轮，直到达到足够的信心。在某些情况下，可能信任证明者并只需要 50%的信心，这意味着必须执行 5 次检查，在其他需要 95%信心的情况下，必须检查所有单元。显然，这种证明协议的缺点是必须进行与元素数量成比例的检查次数，如果我们处理的是数百万个元素的数组，这是不切实际的。

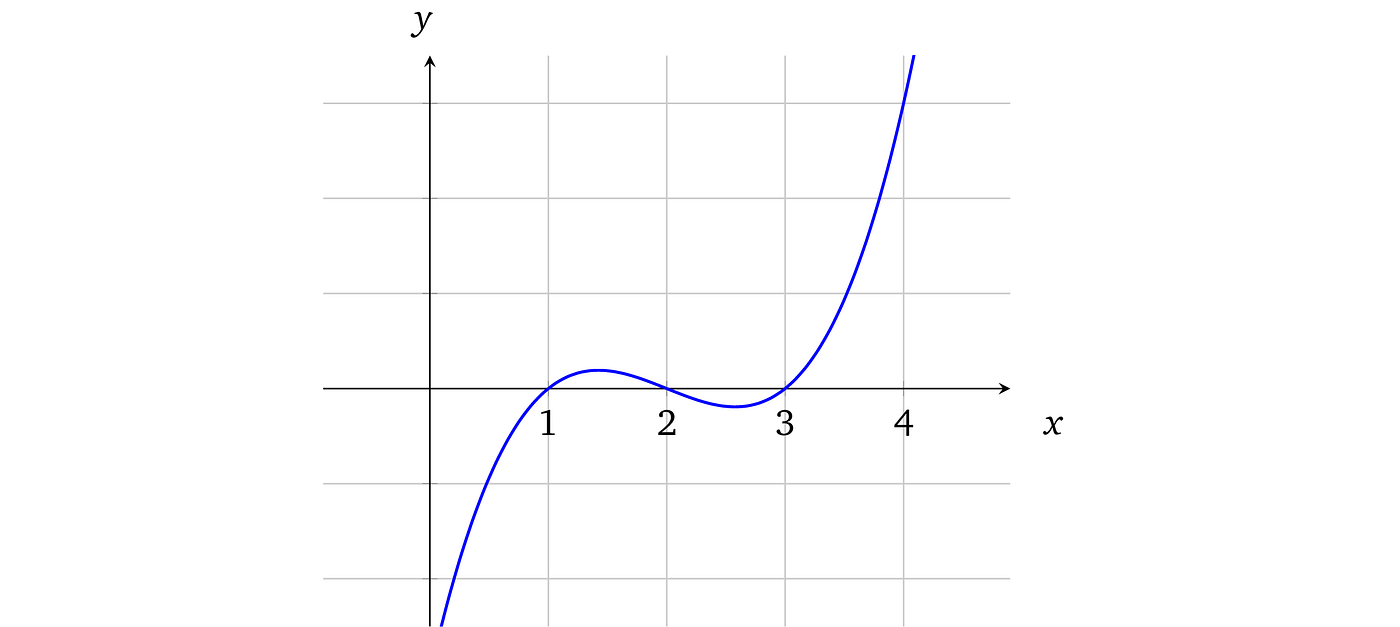
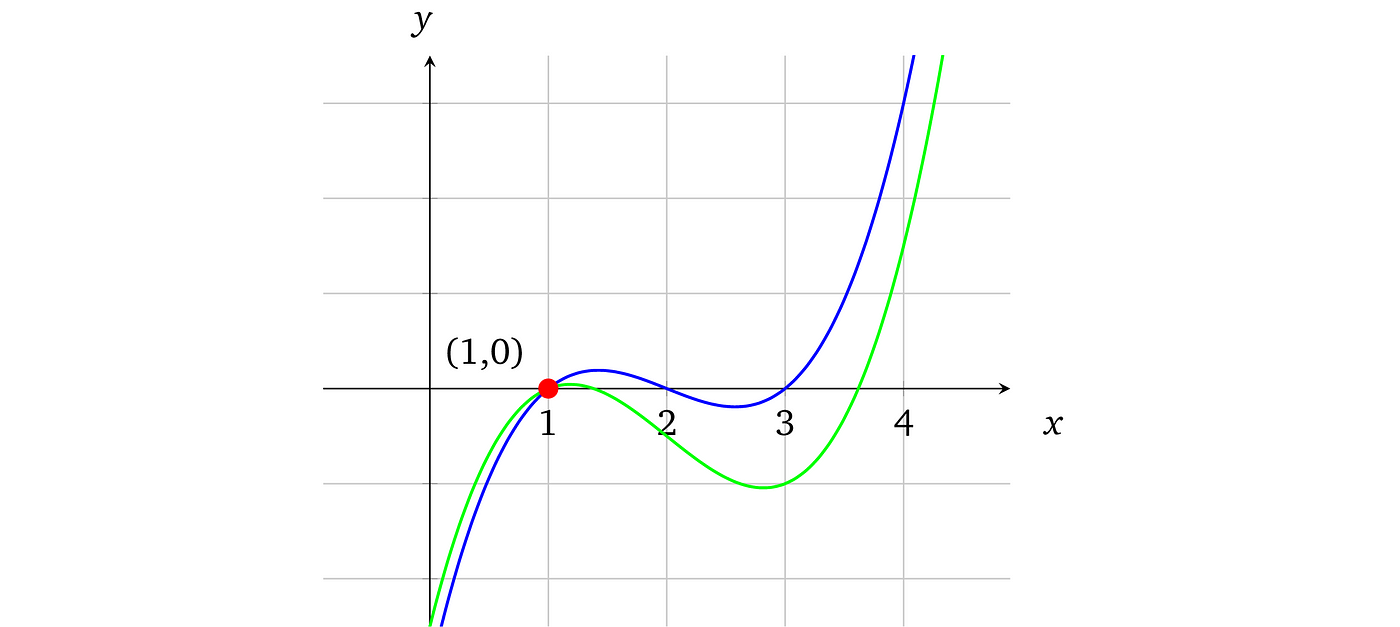
让我们考虑多项式，它可以在图表上可视化为曲线，由数学方程式形成：

上述曲线对应于多项式：$ f(x) = x³ – 6x² + 11x – 6 $。多项式的次数由其最大的 x 指数决定，在这种情况下是 3。

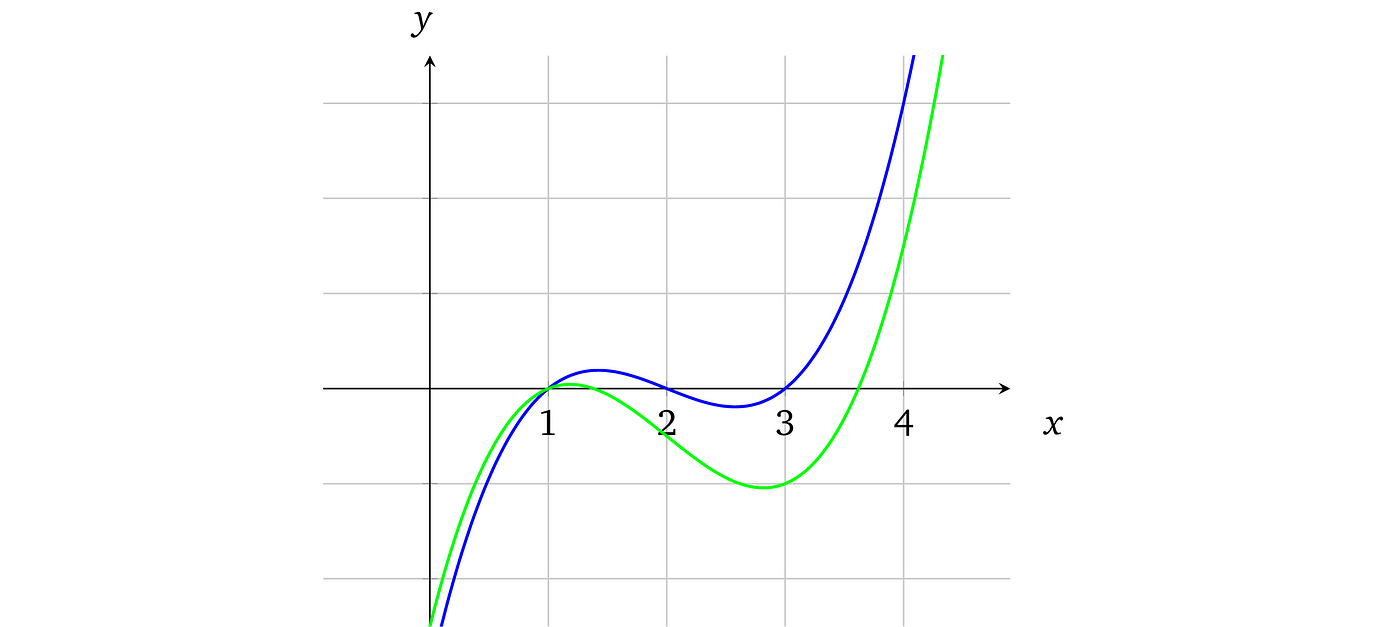
多项式具有一个有利的属性，即如果我们有两个不相等的次数最多为 d 的多项式，它们最多只能在 d 个点相交。例如，让我们稍微修改原始多项式 $x³ – 6x² + 10x – 5$ 并用绿色可视化它：

如此微小的变化会产生截然不同的结果。事实上，不可能找到两个不相等的多项式，它们共享一段连续的曲线（不包括单点段的情况）。

这种属性源于寻找共享点的方法。如果我们想找到两个多项式的交点，我们需要将它们等同。例如，要找到多项式穿过 x 轴的点（即，f(x) = 0），我们将 $x³ – 6x² + 11x – 6 = 0$，并且这种方程的解将是那些共享点：x= 1, x = 2 和 x = 3，你也可以清楚地看到这在前面的图表中是正确的，蓝色曲线穿过 x-轴线。

同样，我们可以将原始和修改版本的多项式等同以找到它们的交点。

结果多项式的次数为 1，显然的，解是 x \= 1。因此只有一个交点：

任意次数 d 多项式的这种方程的结果总是另一个次数最多为 d 的多项式，因为没有乘法产生更高的次数。例如：$5x³ + 7x² – x+ 2 = 3x³ – x² + 2x – 5$，简化为 $2x³ + 8x² – 3x + 7 = 0$。代数学基本定理告诉我们，次数为 d 的多项式最多可以有 d 个解（在后续部分中会详细介绍），因此最多有 d 个共享点。因此，我们可以得出结论，在任意点对多项式进行求值（更多关于多项式求值的信息：[Pik13]）类似于其唯一身份的表示。让我们在 x \= 10 处对我们的示例多项式进行求值。

实际上，在所有选择的 x 中，只有最多 3 个选择在这些多项式中的求值是相等的，其他所有选择都会有所不同。

这就是为什么如果证明者声称知道某个多项式（无论其次数多大），而验证者也知道，他们可以遵循一个简单的协议：

• 验证者选择一个随机值 x 并在本地对多项式进行求值
• 验证者将 x 给证明者并要求对该多项式进行求值
• 证明者在 x 处对他的多项式进行求值并将结果给验证者
• 验证者检查本地结果是否等于证明者的结果，如果是，则该声明以高置信度被证明

例如，如果我们考虑 x 从 1 到 10⁷⁷ 的整数范围，不同求值的点数是 10⁷⁷ – d。因此，x 意外“击中”任何 d 个共享点的概率等于（被认为是可以忽略的）：

注意：新协议只需要一轮，并且在声明中的置信度极高（假设 d 远小于范围的上限）相比低效的位检查协议。

这就是为什么多项式是 zk-SNARK 的核心，尽管可能还存在其他证明媒介。

继续阅读第二部分…

参考文献

[Bit+11] — Nir Bitansky, Ran Canetti, Alessandro Chiesa, and Eran Tromer. From Extractable Collision Resistance to Succinct Non-Interactive Arguments of Knowledge, and Back Again. Cryptology ePrint Archive, Report 2011/443. https://eprint.iacr.org/2011/443. 2011

[Par+13] — Bryan Parno, Craig Gentry, Jon Howell, and Mariana Raykova. Pinocchio: Nearly Practical Verifiable Computation. Cryptology ePrint Archive, Report 2013/279. https://eprint.iacr.org/2013/279. 2013

[Rei16] — Christian Reitwiessner. zkSNARKs in a Nutshell. 2016. url: https://blog.ethereum.org/2016/12/05/zksnarks-in-a-nutshell/ (visited on 2018–05–01)

[But16] — Vitalik Buterin. Quadratic Arithmetic Programs: from Zero to Hero. 2016. url: https://medium.com/@VitalikButerin/quadratic-arithmetic-programs-from-zero-to-hero-f6d558cea649 (visited on 2018–05–01)

[But17] — Vitalik Buterin. zk-SNARKs: Under the Hood. 2017. url: https://medium.com/@VitalikButerin/zk-snarks-under-the-hood-b33151a013f6 (visited on 2018–05–01)

[Gab17] — Ariel Gabizon. Explaining SNARKs. 2017. url: https://z.cash/blog/snark-explain/ (visited on 2018–05–01)

[Ben+14] — Eli Ben-Sasson, Alessandro Chiesa, Christina Garman, Matthew Green, Ian Miers, Eran Tromer, and Madars Virza. Zerocash: Decentralized Anonymous Payments from Bitcoin. Cryptology ePrint Archive, Report 2014/349. https://eprint.iacr.org/2014/349. 2014

[GMR85] — S Goldwasser, S Micali, and C Rackoff. “The Knowledge Complexity of Interactive Proof-systems”. In: Proceedings of the Seventeenth Annual ACM Symposium on Theory of Computing. STOC ’85. Providence, Rhode Island, USA: ACM, 1985, pp. 291–304. isbn: 0–89791–151–2. doi: 10.1145/22145.22178. url: http://doi.acm.org/10.1145/22145.22178

[BFM88] — Manuel Blum, Paul Feldman, and Silvio Micali. “Non-interactive Zero-knowledge and Its Applications”. In: Proceedings of the Twentieth Annual ACM Symposium on Theory of Computing. STOC ’88. Chicago, Illinois, USA: ACM, 1988, pp. 103–112. isbn: 0–89791–264–0. doi: 10.1145/62212.62222. url: http://doi.acm.org/10.1145/62212.62222

[Gro10] — Jens Groth. “Short pairing-based non-interactive zero-knowledge arguments”. In: International Conference on the Theory and Application of Cryptology and Information Security. Springer. 2010, pp. 321–340

[Gen+12] — Rosario Gennaro, Craig Gentry, Bryan Parno, and Mariana Raykova. Quadratic Span Programs and Succinct NIZKs without PCPs. Cryptology ePrint Archive, Report 2012/215. https://eprint.iacr.org/2012/215. 2012

[Pik13] — Scott Pike. Evaluating Polynomial Functions. 2013. url: http://www.mesacc.edu/~scotz47781/mat120/notes/polynomials/evaluating/evaluating.html (visited on 2018–05–01)

我是 AI 翻译官，为大家转译优秀英文文章，如有翻译不通的地方，在这里修改，还请包涵～