探秘 Circle STARKs （重排版）

  • XPTY
  • 更新于 2024-08-06 21:06
  • 阅读 432

探秘 Circle STARKs

原文：https://vitalik.eth.limo/general/2024/07/23/circlestarks.html
作者：Vitalik Buterin
译者：Kurt Pan

本文假设你熟悉 SNARK 和 STARK 工作原理的基础知识；如果你并不熟悉，建议阅读此文的前几节。特别感谢 Eli ben-Sasson、Shahar Papini、Avihu Levy 和 starkware 的其他人员提供的反馈和讨论。

过去两年中，STARK 协议设计中最重要的趋势是转向在小域上工作。STARK 最早的生产实现是在 256 比特域上工作的 - 即模大整数（比如 21888...95617 $ \approx 1.51 * 2^{253}$ ）的算术- 这使得这些协议天然兼容去验证基于椭圆曲线的签名，并使之易于处理。但这也导致了低效：大多数情况下，我们实际上没有很好的方法来利用起这些大数，于是最终大多数情况都浪费了空间，甚至浪费了更多的计算，因为对 4 倍大的数进行算术运算需要多 ~9 倍 的计算时间。为了解决这个问题，STARK 开始在更小的域上工作：首先是 Goldilocks域（模数为 $ 2^{64} - 2^{32} + 1 $ ），然后是 Mersenne31 和 BabyBear域（模数分别为 $ 2^{31} - 1 $ 和 $ 2^{31} - 2^{27} + 1 $）。

这一转变已经使得证明速度大幅提升，最显著的是 Starkware 能够在一台 M3 的笔记本电脑上每秒证明 620,000 个 Poseidon2 哈希。具体来说这意味着，只要我们愿意信任 Poseidon2 作为哈希函数的部分，那么构建一个高效的 ZK-EVM 中最困难的部分之一就已经得到了高效解决。但这些技术是如何工作的，密码学证明（通常需要大整数来保证安全性）是如何在这些域上构建的？以及这些协议与更奇特的构造（比如 Binius）又如何比较？这篇文章将探讨其中的一些微妙差别，会特别关注一种称为 Circle STARKs 的构造（在 Starkware 的 stwo、Polygon 的 plonky3 和 我自己的python 实现 中有实现），其具有一些独特的性质，旨在与高效的 Mersenne31 域兼容。

小域常见的问题

在进行基于哈希的证明（或实际上任何类型的证明）时，最重要的“技巧”之一是用证明有关多项式在随机点的求值以代替证明有关底层多项式的事情。

例如，假设一个证明系统要求你对多项式 $A$ 进行承诺，该承诺必须满足 $A^3(x) + x - A(w x) = x^N$ （ZK-SNARK 协议中一种非常常见的声明类型）。协议会要求你选择一个随机坐标 $r$，并证明 $A(r) + r - A(w r) = r^N$。然后反过来，为了证明 $A(r) = c$ ，你证明 $ Q = \frac {A - c} {X - r} $ 是一个多项式（而不是一个分数表达式）。

如果你提前知道 ，你总是可以欺骗这些协议。在这种情况下，你可以将 $A(r)$ 设置为零，调整 $A(w * r)$ 以满足方程，然后让 $A$ 成为通过这两个点的线。对于第二步也类似，如果提前知道 $r$ ，可以生成你想要的任何 $Q$ ，然后调整 $A$ 以匹配之，即使 $A$ 是只是分数（或其他非多项式）表达式。

为了防止这些攻击，我们需要在攻击者提供 $A$ 之后选择 $r$ （“Fiat-Shamir 启发式”是将 $r$ 设置为 $A$ 的哈希值的别名）。重要的是， 我们需要从一个足够大的集合中选择 $r$ ，以使攻击者无法猜到 。

在基于椭圆曲线的协议甚至于 2019 时代的 STARK 中，这是很平凡的：我们所有的数学运算都是在 256 比特的数上完成的，因此我们选择 $r$ 作为一个随机的 256 比特数，这样就没问题了。而对于小域上的 STARK，我们遇到了一个问题：只有大约 20 亿个可能的 $r$ 值可供选择，因此想要伪造证明的攻击者只需尝试 20 亿次 - 虽然工作量挺大，但对于坚定的攻击者来说算是相当可行的！

这个问题有两个自然的解决方案：

  • 执行 多次随机检验

  • 扩域

执行多次随机检验的方法直观且简单：不是检验一个坐标，而是在四个随机坐标处重复检验。这在理论上是可行的，但存在效率问题。如果你处理的是大小为 $p$ 的域上的次数 < $N$ 的多项式，攻击者实际上可以做出在 $N$ 个位置上“看起来”不错的坏多项式。因此，其破解一轮协议的几率是 $ \frac N P$ 。例如，如果 $ p = 2^{31} - 1 $ 和 $ N = 2^{24} $，则意味着攻击者每轮只能获得 7 位安全性，因此你需要进行 18 轮左右而不是 4 轮，才能对此类攻击者具有足够的可靠性。理想情况下，我们会做 $k$ 倍的工作，但只需从安全级别中减去 $N$ 一次。

这让我们转向另一个解决方案： 扩域 。扩域类似于复数，但是在有限域上：我们想象存在一个新值，将其称为 $i$，并宣称 $i^2 = -1 $。则乘法变为 $(a + bi) * (c + di) = (ac - bd) + (ad + bc) i$。我们现在可以对$(a, b)$ 对进行操作，而不仅仅是单个数字。假设我们在大小为 $ \approx 2^{31} $ 的域（如 Mersenne 或 BabyBear）上工作，这将使我们有 $ \approx 2^{62} $ 个值可供选择 。为了进一步提高，我们再次应用相同的技术，但我们已经使用了 $i$ ，因此我们需要定义一个不同的新值：在 Mersenne31 中，我们选择 $w$ ，其中 $w^2 = -2i - 1$。则乘法现在变为

$(a + bi + cw + diw) * (e + fi + gw + hiw) = ...$

image.png

这里实现不是最优的（可以用Karatsuba优化），只是展示原理

现在，我们有大约 $2^{124}$ 个值可供选择 $r$，这对于我们的安全需求来说已经足够高了：如果我们处理的是次数小于 $2^{20}$ 的多项式，那么一轮下来我们就能获得 104 比特的安全性。如果我们想要更加谨慎，达到更广泛接受的 128 比特安全级别，我们可以在协议中添加一些工作量证明。

请注意，我们实际上只在 FRI 协议中使用此扩域，以及需要随机线性组合的其他情况。大部分数学运算仅在“基域”（模数 $2^{31} - 1$ 或 $15 * 2^{27} + 1 $ ）上完成，以及几乎所有的哈希后的数据都在基域上，因此每个值仅哈希四个字节。这让我们既能从小域的效率中受益，又能在需要时出于安全考虑而使用更大的域。

常规 FRI

构建 SNARK 或 STARK 时，第一步通常是算术化：将任意计算问题归约为一些变量和系数为多项式的方程（例如，方程通常看起来像 $C(T(x), T(next(x))) = Z(x) * H(x) $ 这种，其中给定 $C$ 、$next$ 和 $Z$，求解者需要给出 $T$ 和 $H$ ）。一旦有了这样的方程，方程的解就对应于底层计算问题的解。

为了证明你有一个解，你需要证明你提出的值实际上是真的多项式（而不是分数，或者在一个地方看起来像一个多项式而在另一个地方看起来像另一个多项式的数据集，或者......），且具有特定的最大次数。为了做到这一点，我们迭代地应用随机线性组合技巧：

  • 假设你有一个多项式 $A$ 的求值，并且你想证明它的次数 $< 2^{20}$

  • 考虑多项式 $B(x^2) = A(x) + A(-x) $ 和 $C(x^2) = \frac {A(x)-A(-x)} {x} $ 。

  • 令 $D$ 为随机线性组合 $B + rC$

本质上发生的事情是 $B$ 分离出了 $A$ 的偶数项系数，而 $C$ 分离出了奇数项系数。给定 $B$ 和$C$ ，可以恢复出 $A(x) = B(x^2) + xC(x^2)$ ：。如果 $A$ 确实有次数$< 2^{20}$ ，则 (i) $B$ 和 $C$ 有次数$< 2^{19}$ 。且作为随机线性组合， $D$ 也必须有次数$< 2^{19}$ 。

我们已经将“证明次数小于 $2^{20}$ 的问题归约为“证明次数小于 $2^{19}$ ”问题。重复此操作 20 次，你就得到了被称为“快速 Reed-Solomon 交互式预言邻近性证明”或“FRI”的技术。如果有人试图通过此技术输入某个不是次数小于 $2^{20}$ 的多项式的东西，那么第二轮输出（以 $ \approx 1 - \frac 1 {2^{124}} $的概率）将不是次数小于 $2^{19}$ 的多项式，第三轮输出将不是次数小于 $2^{18}$ 的东西，依此类推，最后的最终检验将失败。在大多数位置上等于次数小于 $2^{20}$ 的多项式的数据集是有机会通过该方案，但为了构造这样的数据集，你需要知道底层多项式，因此即使是这种略有缺陷的证明也是一个令人信服的论据，即证明者如果愿意的话可以生成“真实”的证明。证明这点适用于所有可能的输入还存在进一步的技术复杂性；了解这方面的细节一直是过去五年来 STARK 学术研究的主要重点。

让我们更详细地看看这里发生了什么，以及哪些性质是使这一切正常工作所必需的。在每一步中，我们将 次数 减少了 2 倍，以及我们还将 求值域（我们正在查看的点集）减少了 2 倍。前者是使 FRI 完全起作用的原因。后者使它如此之快的原因：因为每一轮都比前一轮小 2 倍，所以总开销是 $O(N)$ 而不是 $O(N * log(N)$。

为了完成这个求值域缩减，我们需要一个二对一映射 $ {x, -x} \Rightarrow x^2 $。这种二对一映射的优点在于它是可重复的：如果你从一个乘法子群（集合 $ {1, w, w^2, ... w^{n-1}} $ ）开始，那么你就是从一个对于集合中的任何 $x$ ，$-x$ 也在该集合中的集合开始（比如 $x = w^k, -x = w^{k\pm \frac N 2 }$ ），如果再你将其平方得到 $ {1, w^2, {(w^2)}^2, ... {(w^2)}^{n-1}} $ ） ，那么完全相同的性质适用，因此你可以继续一直减少到一个值（尽管在实践中我们通常会早一点停止）。

image.png

你可以把这想作是一个绕着一个圆连线的操作，然后拉长该连线直到它沿着圆旋转两周。x 次的点变成 2x 次的点。0...179 次的每个点都有一个 180...359 次的对应点，而且最终会与这些点重叠。你可以反复重复此过程。

为了使这个工作，你需要原始乘法子群的大小有 2 的大幂次作为因子。BabyBear 的模数为 $15 2^{27} + 1$ ，因此最大可能的子群都是非零值 - 因此大小为 $15 2^{27} $。这对上述技术非常友好。可以取大小为 $2^{27} $ 的子群，或者可以只取该全集，执行 FRI 将多项式一直降到 15 次，然后在最后直接检验次数。然而，Mersenne31 不以这种方式工作。模数为 $2^{31} -1 $，因此乘法子群的大小为 $2^{31} -2 $ 。这只能除以 2 一次。从那时起，我们就无法进行 FFT - 至少不能使用上述技术。

这是一个悲剧，因为 Mersenne31 是一个使用现有 32 比特 CPU/GPU 进行算术操作 超级方便 的域。如果将两个数字相加，结果可能超过 $2^{31} -1 $，但你可以通过执行 $ x \Rightarrow x + (x >> 31) $ 来约简之，其中 $>> $ 是位移位。对于乘法，你可以做类似的事情，但需要使用一个特殊的（但通常可用的）操作码来返回乘法结果的“高阶位”（即 ）。这使得算术效率比 BabyBear 高出约 1.3 倍。如果我们可以在 Mersenne31上 进行 FRI，那么事情就会好很多。

Circle FRI

这就是 circle STARKs 巧妙之处。给定一个素数 $p$，事实表明我们依然可以很容易得到一个具有类似二对一性质的大小为 $p+1$ 的群：点集 $(x, y)$，其中 $ x^2 + y ^2 = 1$。让我们看看这个结构模 31 的样子：

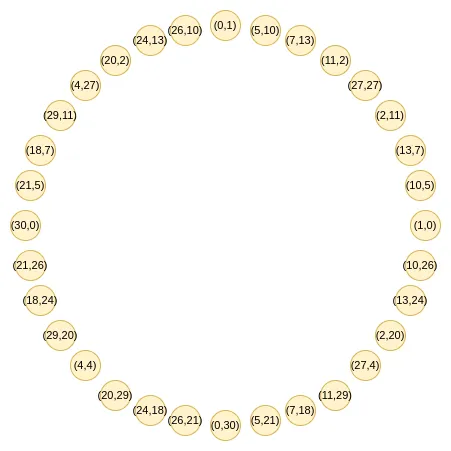
image.png

这些点遵循加法律，如果你最近学过 三角学 或 复数乘法，你可能会觉得这个定律很熟悉： 

加倍形式为：
$ 2 * (x, y) = (2x^2 - 1 , 2xy)$

现在，让我们只关注这个圆上处于“奇数”位置的点：


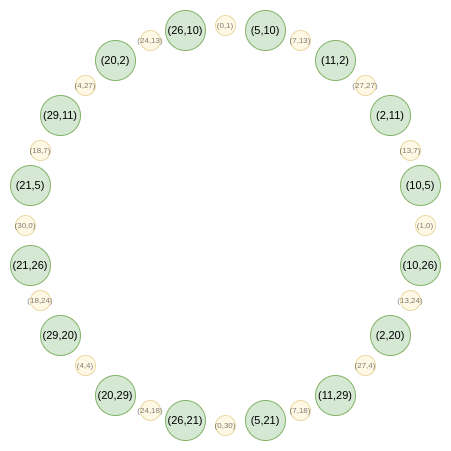
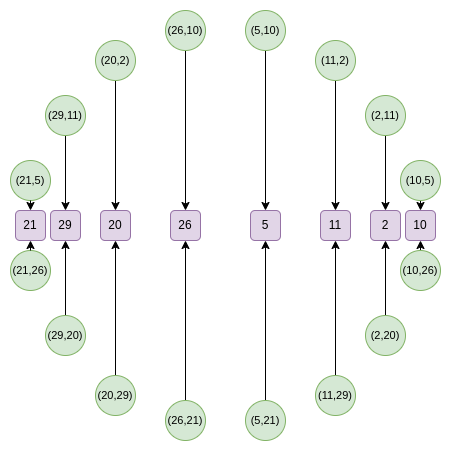
现在，这就是我们的 FFT了。首先，我们将所有点一条竖线上的点合并。和常规 FRI 中使用的 和 公式等价的公式是：

$$ f_0(x)= \frac { F(x,y) + F(x, -y)} {2} $$

$$ f_1(x)= \frac { F(x,y) - F(x, -y)} {2y}$$

然后我们可以取一个随机线性组合，得到一个位于 x 线子集上的一维 $F$：

从第二轮往后，映射改变：

$$ f_0(2x^2 - 1)= \frac { F(x) + F(-x)} {2} $$

$$ f_1(2x^2 - 1)= \frac { F(x) - F(-x)} {2x}$$

而这个映射实际上输入了上述集合，并且每次都将其大小缩小一半！这里发生的事情是，每个 $x$ 在某种意义上“代表”两个点：$(x, y)$ 和 $(x, -y)$ 。而 $ x \Rightarrow 2x^2 - 1 $ 就是上面的点加倍法则。因此，我们取圆上两个相对点的 $x$ 坐标，并将其转换为倍点的 $x$ 坐标。

例如，如果我们取右边第二个的值，$2$ ，并应用映射，我们得到了$ 2(2^2) - 1 = 7 $ 。如果我们回到原始圆， $(2, 11)$是从右边逆时针方向的第三个点，因此如果我们将其加倍，我们得到了从右边逆时针方向的第六个点，即... $(7, 13)$。

这一切都可以在二维上完成，但在一维上操作会使事情更高效。

Circle FFTs

与 FRI 密切相关的一种算法是 快速傅里叶变换，输入次数小于 $n$ 的多项式的 $n$ 个求值的集合，将其转换为多项式的 $n$ 个系数。FFT 遵循与 FRI 相同的路径，只不过它不是在每一步生成 $f_0$ 和 $f_1$ 的随机线性组合，而是在两者之上递归地应用一半大小的 FFT，然后将 $FFT(f_0)$ 的输出作为偶数系数，将 $FFT(f_1)$ 的输出作为奇数系数。

圆群也支持 FFT，它也是由类似方式的 FRI 构造的。但是， 一个关键的区别是circle FFT（和circle FRI）所处理的对象技术讲并不是多项式 。相反，它们是数学家所说的 Riemann-Roch 空间：在这种情况下，多项式要“模上”圆 ($x^2 + y^2 - 1 = 0$)。也就是说，我们将 $x^2 + y^2 - 1 $ 的任何倍数视为等于零。另一种思考方式是：我们只允许 $y$ 的 1 次幂：一旦我们得到 $y^2$ 项，我们就用 $1 - x^2$ 替换它。

这意味着的另一点是， circle FFT 输出的“系数”不像常规 FRI 那样是单项式（例如如果常规 FRI 输出 $[6, 2, 8, 3 ]$ ，那么我们知道这意味着 $ P(x) = 3x^3 + 8x^2 + 2x = 6 $ ）。相反，这些系数是circle FFT 特有的一个奇特的基：

$$ {1, y, x, xy, 2x^2 - 1, 2x^2y-y, 2x^3y-xy, 8x^4-8x^2 + 1 ... } $$

好消息是，作为一名开发者，你几乎可以完全忽略这些。STARK 从来不会让你需要知道这些系数。相反，你可以始终将“多项式”存储为特定求值域上的一组值。唯一需要使用 FFT 的地方是执行（Riemann-Roch空间版本的）低次扩展：给定 $N$ 个值，生成位于同一多项式上的 $k N$ 个值。在这种情况下，你可以执行 FFT 来生成系数，将 $(k-1) n$ 个零附加到这些系数，然后执行逆 FFT 以返回更大的求值集。

Circle FFT 并不是唯一的一种“奇异 FFT”。椭圆曲线 FFT 功能更加强大，因为它们适用于任何有限域（素数、二进制等等）。但是，ECFFT 理解起来更加复杂，效率更低，由于我们已经可以对 $p = 2^{31} - 1$ 使用circle FFT，所以我们就这样做了。

从这里开始，让我们来了解一些更深奥的细节，对于实现circle STARK 的人来说，与常规 STARK 相比，这些细节会有所不同。

取商

在 STARK 协议中，一个常见做法是取特定点的商，这些点可以是有意选择的，也可以是随机选择的。例如，如果你想证明 $P(x) = y$ ，可以通过提供 $Q = \frac {P-y} {X - x} $ ，并证明 $Q$ 是一个多项式（而不是一个分数值）来证明。DEEP-FRI 协议 中使用了随机选择求值点，这让 FRI 能够以更少的 Merkle 分支保证安全。

这里，我们遇到了一个微妙的挑战：在圆群中，没有类似于常规 FRI  $ {X - x} $的线性函数，它只经过一个点。这在几何上是可见的：

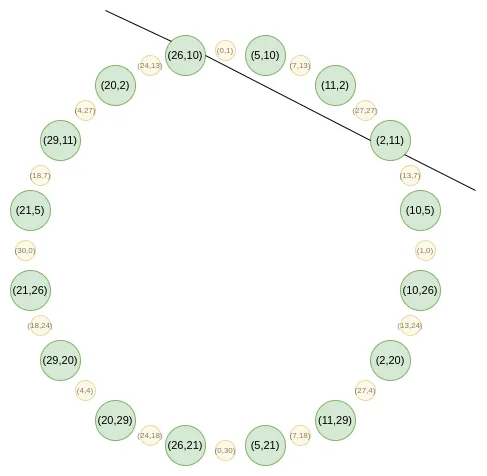
image.png

你可以使线函数与一个点 $(P_x, P_y)$ 相切，但该函数将通过“重数为 2”的点 - 也就是说，多项式要成为该线函数的倍数，它必须满足比在该点为零更严格的条件。因此你无法仅在一个点处证明求值。那么我们该怎么做呢？基本上，我们迎难而上，在两个点处证明求值，添加一个我们不需要关心其求值的虚拟点。

image.png

线函数：$ax + by +c $ . 如果将其转换为一个方程，强制令其等于 0，那么你可能会认出其为高中数学所称的“直线的标准式”。

如果我们有一个多项式 $P$ ，它在$P_1$ 处等于$v_1$ ，在 $P_2$ 处等于$v_2$ ，那么我们选择一个插值函数 ：一个在 $P_1$ 处等于 $v_1$，在 $P_2$ 处等于 $v_2$ 的线函数。这可以化简为 $ v_1 + (v_2 - v_1) * \frac {y-y_1} {(P_2)_y - (P_1)_y}$。然后我们通过减去 $I$ （因此 $P-I$ 在两点都等于零）、除以 $L$（ $P_1$和 $P_2$ 之间的线函数），并证明商 $ \frac {P - I} {L}$ 是多项式来证明 $P$ 在 $P_1$ 处等于 $v_1$，在 $P_2$ 处等于 $v_2$。

消失多项式

在 STARK 中，你要证明的多项式方程通常看起来像 $C(P(x), P(next(x))) = Z(x) * H(x)$ 这种，其中 是在整个原始求值域中等于零的多项式。在“常规”STARK 中，这个函数就是 $x^n - 1$。在circle STARK 中，等价的函数是：

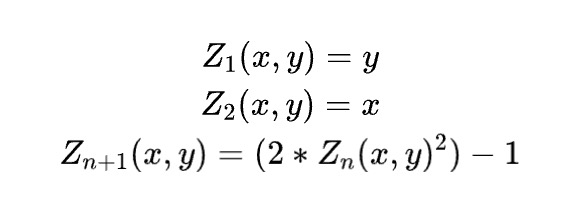
image.png

请注意，你依然可以从折叠函数中推导出消失多项式：在常规 STARK 中是重复 $ x \rightarrow x^2$，在这里是重复 $ x \rightarrow 2x^2 - 1$ ，尽管你在第一轮做了不同的事情，因为第一轮是特殊的。

反转比特序

在 STARK 中，多项式的求值通常不按“自然”顺序排列 $(P(1)、 P(w)、 P(w^2) ... P(w^{n-1}) )$，而是按我所说的“反转比特序”排列：

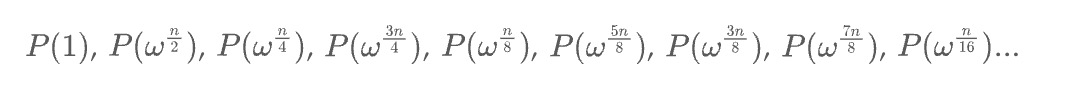
image.png

如果我们令 $n = 16$，而且只关注要求值的 $w$ 的幂，则列表如下所示：

$ {0, 8 , 4, 12, 2, 10, 6, 14, 1, 9, 5, 13, 3, 11, 7, 15 }$

这种排序具有一个关键性质，即在 FRI 求值早期组合在一起的值会在排序中放在一起。例如，FRI 的第一步将 $x$ 和 $-x$ 组合在一起。在 $n=16$ 的情况下，$w^8 = -1$ ，这意味着 $P(w^i)$ 以及 $P(-w^i) = P(w^{i + 8}) $ 。并且，正如我们所见，它们恰好是彼此相邻的对。FRI 的第二步将 $P(w^i)$ 、 $P(w^{i+4})$、 $P(w^{i+8})$和 $P(w^{i+12})$ 组合在一起。它们恰好就是我们看到的四元组。以此类推。这使得 FRI 更加节省空间，因为可以同时为折叠在一起的两个值（或者，如果你一次折叠 $k$ 轮，则为所有的 $2^k$ 个值）提供一个 Merkle 证明。

在circle STARK 中，折叠结构略有不同：第一步，我们将 $(x,y)$ 与 $(x,-y)$ 组合在一起，第二步将 $x$ 与 $-x$ 组合在一起，随后的步骤将 $p$与 $q$ 组合在一起，选择 $p$ 和 $q$ 使得 $Q^i(p) = -Q^i(q)$，其中 $Q^i$ 是映射 $ x \rightarrow 2x^2 - 1$ 重复 $i$ 次。如果我们从它们在圆上的位置来考虑这些点，那么在每一步中，这看起来都像是第一个点与最后一个点配对，第二个点与倒数第二个点配对，等等。

为了调整反转比特序以反映这种折叠结构，我们反转除最后一个比特之外的每个比特。我们保留最后一个比特，并用它来确定是否反转其他比特。

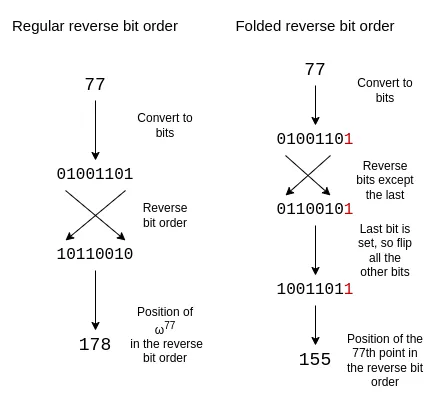
image.png

16折反转比特序如下所示： $ {0, 15, 8 , 7, 4, 11, 12, 3, 2, 13, 10, 5, 6, 9 , 14, 1 }$

如果你看上一节中的圆，第 0、15、8 和 7 个点（逆时针方向，从右侧开始）的形式为 $(x, y)$、 $(x, -y)$、$(-x, -y)$ 和 $(-x, y)$，这正是我们所需要的。

效率

Circle STARKs（以及一般的 31 比特素数 STARK）非常高效。在Circle STARKs 中证明的实际计算很可能涉及几种类型的计算：

  1. 原生算术，用于计数等“业务逻辑”

  2. 原生算术，用于密码学（例如 Poseidon 等哈希函数）

  1. 查找论证，一种通过从表中读取值来实现多种计算的通用方法

衡量效率的关键指标是：你是否使用计算迹中的整个空间来做有用的工作，还是留下了大量浪费的空间？在大域 SNARK 中，存在大量浪费的空间：业务逻辑和查找表主要涉及对小数字的计算（通常在 N 步计算中数字小于 N，因此在实践中小于 $ 2^{56}$ ），但无论如何，你都必须付出使用大小为 $ 2^{256}$ 比特的域的开销。此处，域大小为 $ 2^{31}$，因此浪费的空间并不大。“专为 SNARK 设计”的低算术复杂度哈希（例如 Poseidon）在任何域中迹中使用了每个数字的每一比特。

因此，circle STARK 实际上非常接近最优了！Binius 甚至更强大，因为它允许混合搭配不同大小的域，从而为所有东西给出更高效的位打包。Binius 还提供了执行 32 比特加法的选项，且无需产生查找表的开销。然而，这些收益是以（在我看来）显著更高的理论复杂性为代价的，而circle STARK（以及基于 BabyBear 的常规 STARK）在概念上是相当简单的。

结论：我对 circle STARKs 怎么看？

与常规 STARK 相比，Circle STARK 并不会给开发者带来太多额外的复杂性。在实现的过程中，上述三个问题基本上就是我看到的与常规 FRI 相比的唯一区别。Circle FRI 所操作的“多项式”背后的数学原理是相当反直觉的，需要一段时间才能理解和领悟。但恰好这种复杂性被隐藏起来了使得开发者不会看到太多。Circle 数学的复杂性是封装过的，而不是系统性的。

通过结合 Mersenne31、BabyBear 和 二进制域技术比如Binius，我们确实感觉得到正在接近 STARK “基础层”效率的极限。在这个时间点，我预计 STARK 优化的前沿将转向对哈希函数和签名等原语进行最高效的算术化（并为此目的优化这些原语本身）、进行递归构造以解锁更多并行化、对虚拟机进行算术化以提升开发者体验，以及其他上层任务。

点赞 0
收藏 0
分享
本文参与登链社区写作激励计划 ，好文好收益，欢迎正在阅读的你也加入。

0 条评论

请先 登录 后评论
XPTY
XPTY
江湖只有他的大名，没有他的介绍。

XPTY

如果觉得我的文章对您有用，请随意打赏。你的支持将鼓励我继续创作！