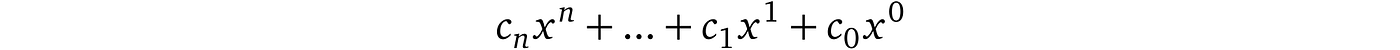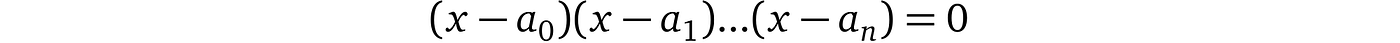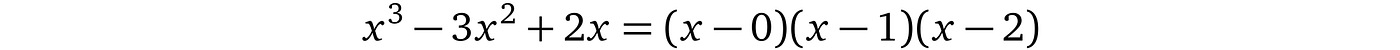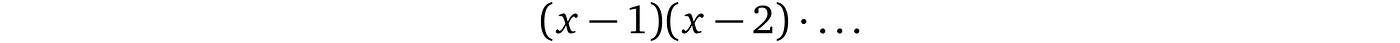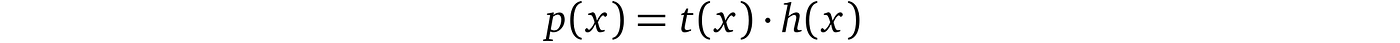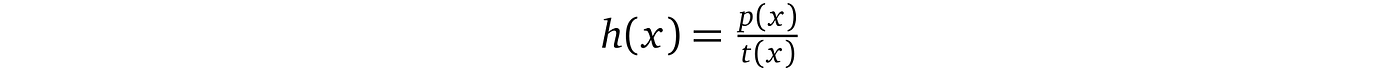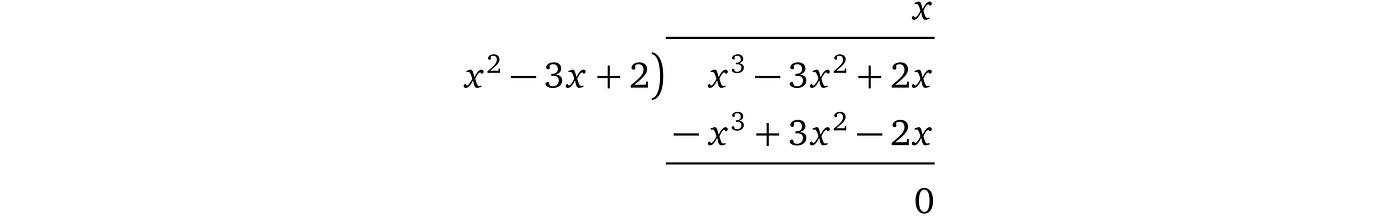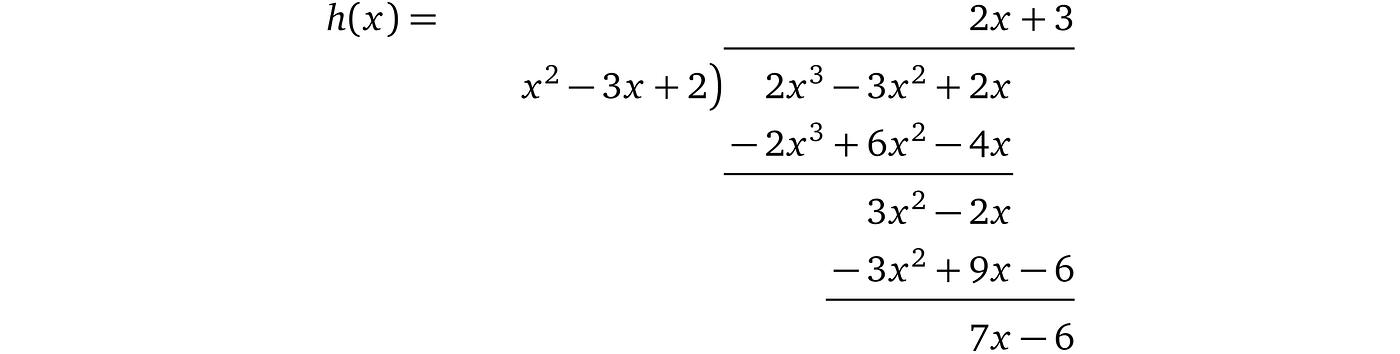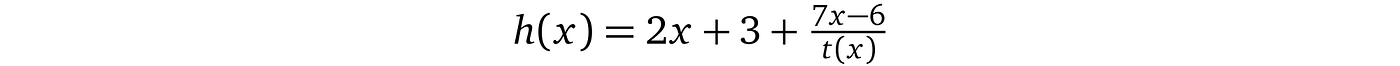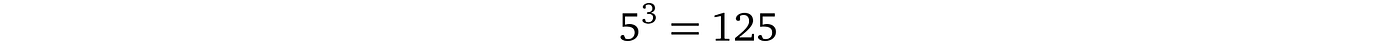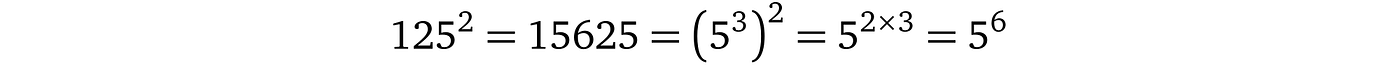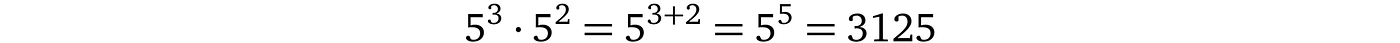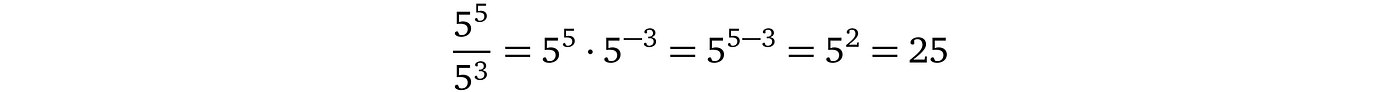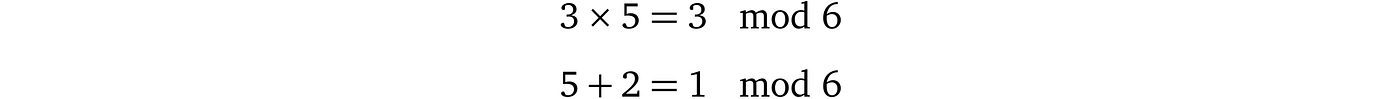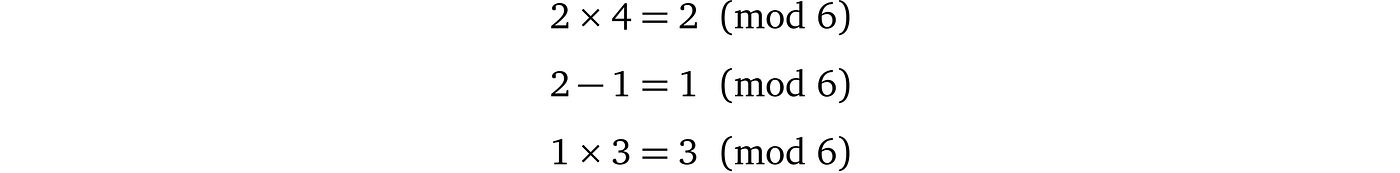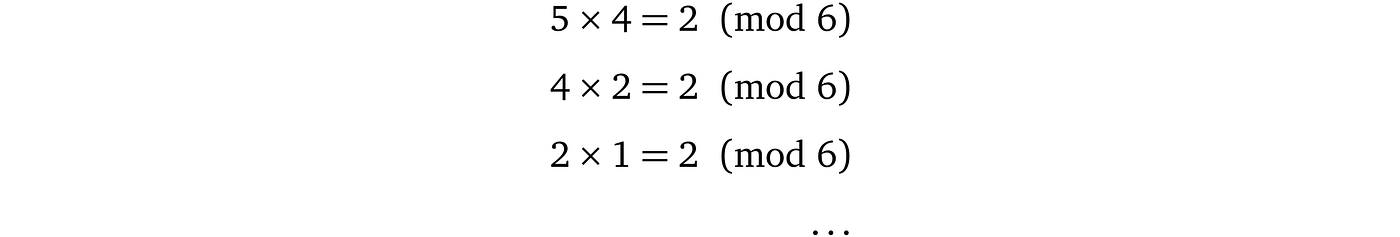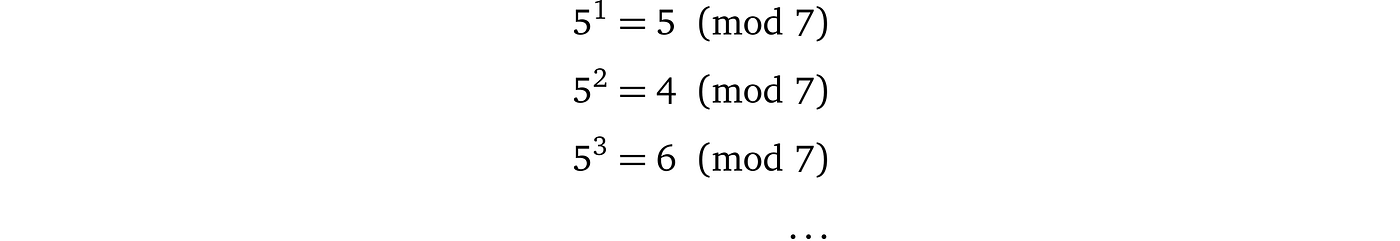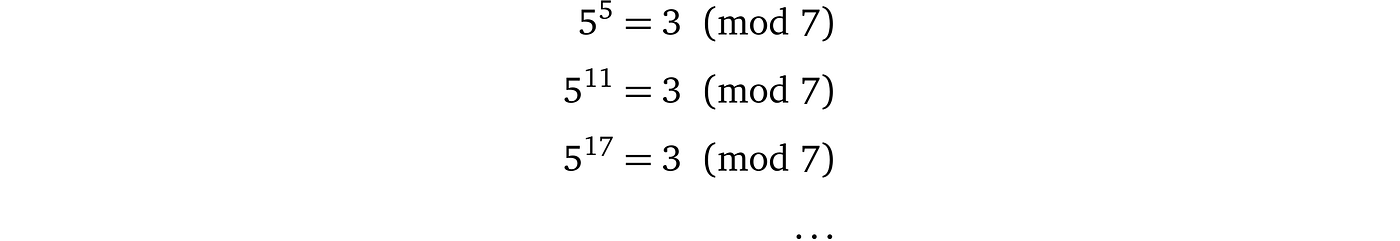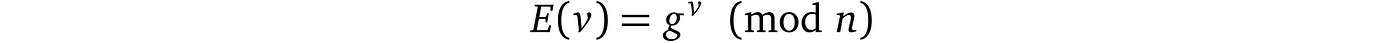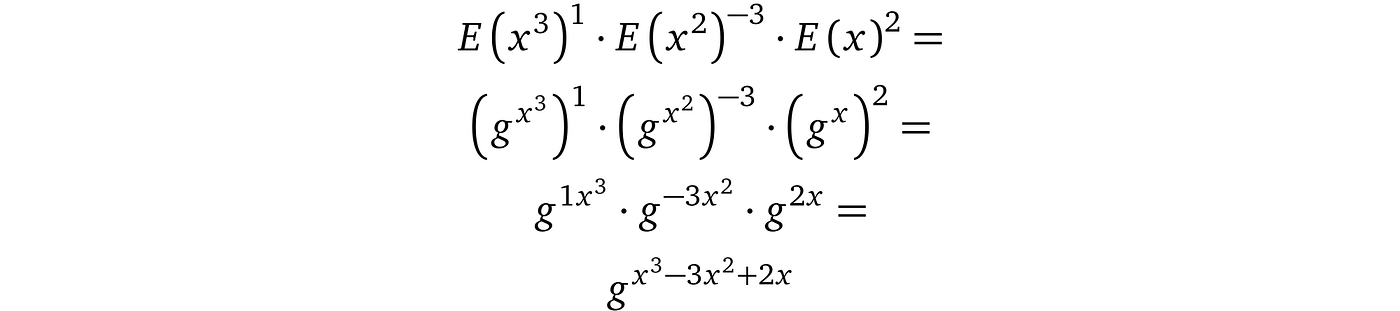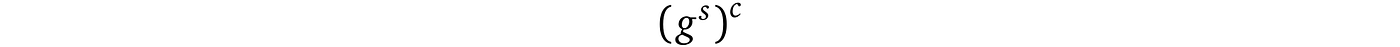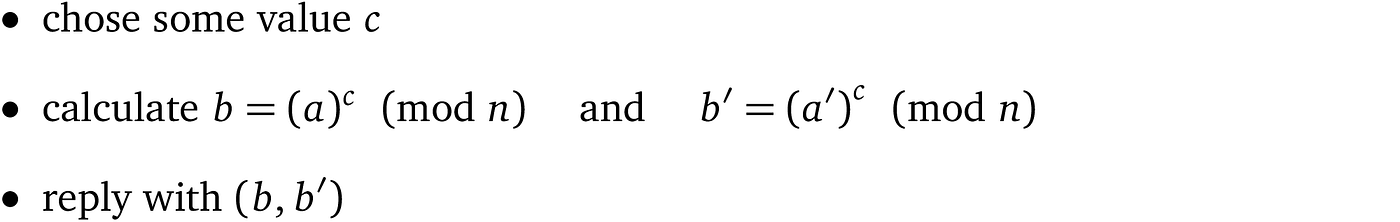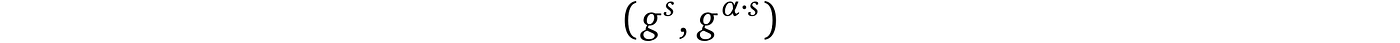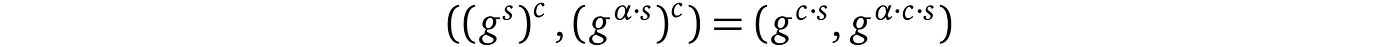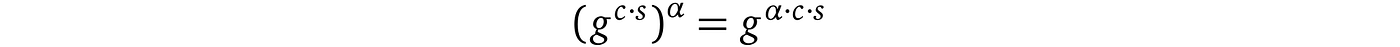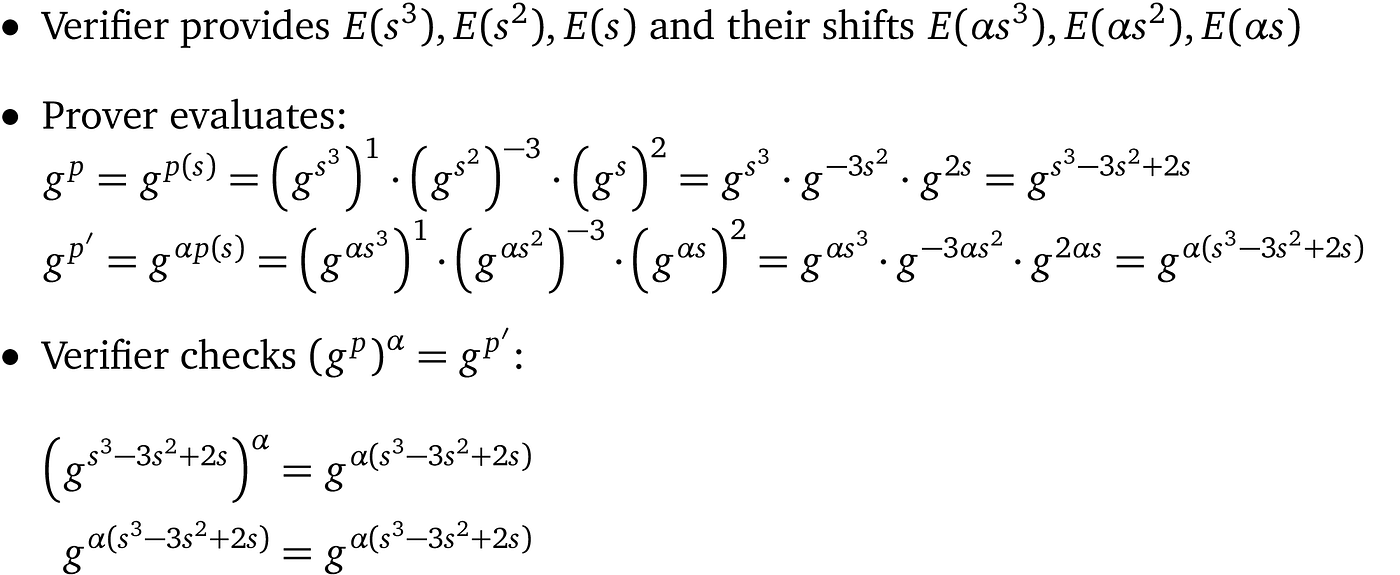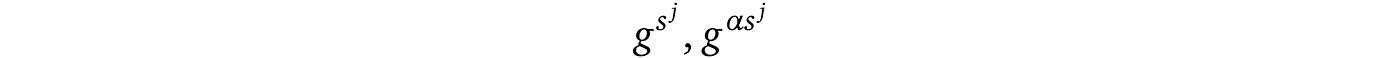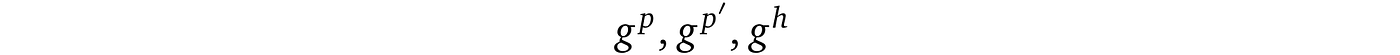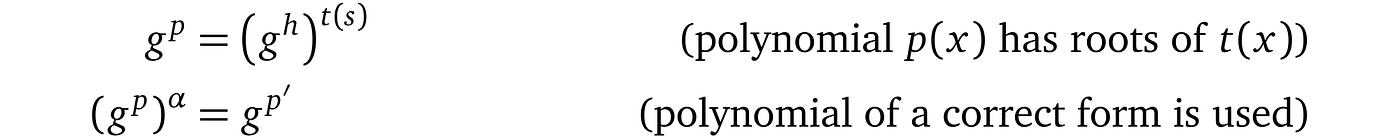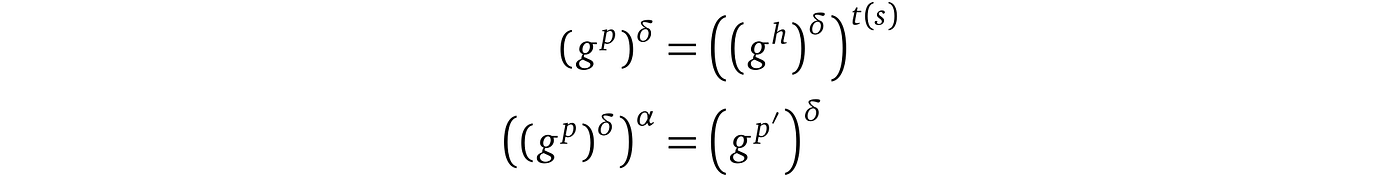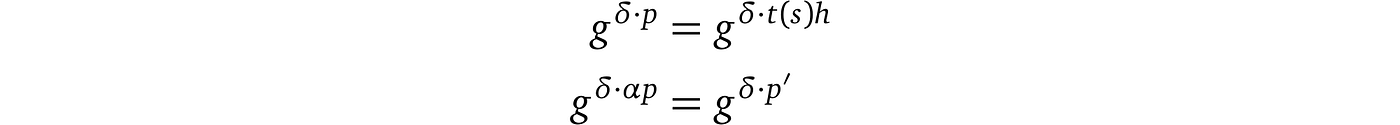zk-SNARK 系列 - #2 证明多项式的知识
- Maksym
- 发布于 2024-08-07 15:20
- 阅读 2999
为什么和如何使用 zk-SNARK系列文章
证明多项式的知识
这是关于为什么和如何使用 zk-SNARK系列文章的第二篇,见第 1 篇
我们从证明多项式知识的问题开始,并逐步采用通用方法。在此过程中,我们将发现多项式的许多其他性质。
到目前为止的讨论集中在一种弱证明概念上,其中各方必须相互信任,因为还没有措施来强制执行协议规则。例如,证明者不需要知道多项式,他可以使用任何其他可用的方法来得出正确的结果。此外,如果验证者的多项式评估范围不大,比如说 10,证明者可以猜一个数字,并且有非忽略的概率会被接受。我们必须解决协议的这种弱点,但首先,知道一个多项式意味着什么?一个多项式可以表示为以下形式(其中 $n$ 是多项式的次数):
如果有人声称他或她知道一个一次多项式(即 $c₁x¹ + c₀ = 0$),这意味着他或她真正知道的是系数$c₀, c₁$。此外,系数可以有任何值,包括 0。
假设证明者声称知道一个三次多项式,使得 x = 1 和 x = 2 是所有可能解中的两个。一个这样的有效多项式是 $x³ – 3x² + 2x = 0$。对于$x$= 1:1 – 3 + 2 = 0。对于 $x$ = 2:8 – 12 + 4 = 0。
让我们首先更仔细地看看解决方案的结构。
因式分解
代数基本定理指出,任何多项式都可以分解为线性多项式(即表示一条线的一次多项式),只要它是可解的。因此,我们可以将任何有效的多项式表示为其因子的乘积:
此外,如果这些因子中的任何一个为零,则整个方程为零,因此所有 a 是唯一的解。事实上,我们的例子可以分解为以下多项式:
解( x 的值)是:0, 1, 2,你可以在多项式的任一形式上轻松检查这一点,但因式分解形式在表面上具有所有解(也称为根)。
回到证明者声称他知道一个具有根 1 和 2 的三次多项式,这意味着他的多项式具有以下形式:
换句话说,( x – 1)和( x – 2)是所讨论多项式的共因子。因此,如果证明者想证明他的多项式确实具有这些根而不披露多项式本身,他需要证明他的多项式 p(x) 是这些共因子 t(x) = (x- 1)(x- 2), p(x) 称为目标多项式,以及某个任意多项式 h(x)(在我们的例子中等于 x – 0)的乘积,即:
换句话说,存在某个多项式 h(x)使得 t(x)等于 p(x),因此 p(x)包含 t(x),因此 p(x) 具有 t(x)的所有根,这是要证明的内容。
找到 h(x)的自然方法是通过除法
如果证明者找不到这样的 h(x),这意味着 p(x)没有必要的共因子 t(x),在这种情况下,多项式除法将有余数。在我们的例子中,如果我们将 $p(x) = x³ – 3x² + 2x$ 除以 $t(x) = (x – 1)(x – 2) = x² – 3x + 2$:
注意:分母在左,结果在右上角,余数在底部(多项式除法解释和示例可在[Pik14]中找到)。
我们得到了结果 h(x) = x,没有余数。
注意:为了简化起见,接下来我们将使用多项式的字母变量来表示其评估,例如,$p = p(r)$
使用我们的多项式身份检查协议,我们可以比较多项式 p(x)和 t(x) ⋅ h(x):
- 验证者随机抽取一个值 r,计算 t = t(r)(即评估)并将 r 给证明者
- 证明者计算 h(x) =p(x) / t(x)并评估 p(r) 和 h(r);将结果值 p, h 提供给验证者
- 验证者然后检查 p = t ⋅ h,如果是这样,这些多项式是相等的,这意味着 p(x)具有 t(x)作为共因子。
为了将其付诸实践,让我们执行此协议以我们的例子为例:
- 验证者随机抽取一个值 23,计算 t = t(23) = (23 – 1)(23 – 2) = 462 并将 23 给证明者
- 证明者计算 h(x) =p(x) / t(x) = x,评估 p = p(23) = 10626 和 h = h(23) = 23 并将 p, h 提供给验证者
- 验证者然后检查 p = t ⋅ h:10626 = 462 ⋅ 23,这是真的,因此声明被证明
相反,如果证明者使用不同的 p′(x),它没有必要的共因子,例如 p′(x) = 2 x ³ – 3 x ² + 2 x ,那么:
注意:尽管作者的主要目标是简化,包括使用的数学符号集,但省略无处不在的符号 prime:′ 将对进一步的部分有害。其主要目的是表示原始变量或函数的某些变换或派生,例如,如果我们想将 v 乘以 2 并将其分配给一个单独的变量,我们可以使用 prime:v ′ = 2 ⋅ v。
我们将得到 2x + 3,余数为 7x –6,即:$p(x) = t(x)×(2x + 3) + 7x –6$。这意味着证明者将不得不将余数除以 t(x)以进行评估:
因此,由于验证者随机选择 x,评估余数 7x – 6 将被 t(x) 的评估均匀整除的概率很低(但仍然不可忽略),因此如果验证者还检查 p 和 h 必须是整数,这样的证明将被拒绝。然而,检查要求多项式系数也是整数,这对协议造成了重大限制。
这就是引入加密原语的原因,使得这种除法变得不可能,即使原始评估恰好是可整除的。
备注 3.1 现在我们可以在不知道多项式本身的情况下检查多项式的特定属性,因此这已经给了我们某种形式的零知识和简洁性。然而,这种构造存在多个问题:
- 证明者可能根本不知道所声称的多项式 $p(x)$。他可以计算评估 t = t(r),选择一个随机数 h 并设置 $p = t⋅h$,这将被验证者接受为有效,因为方程成立。
- 因为证明者知道随机点 x = r,他可以构造任何在 r 处与 t(r) ⋅ h(r) 有一个共享点的多项式。
- 在原始声明中,证明者声称知道一个特定次数的多项式,在当前协议中没有次数的强制。因此,证明者可以通过使用一个更高次数的多项式来作弊,该多项式也满足共因子检查。我们将在以下部分解决所有问题。
模糊评估
备注 3.1 的前两个问题是可能的,因为值以原始形式呈现,证明者知道 r 和 t(r) 。理想情况下,这些值应该作为一个黑盒给出,这样就不能篡改协议,但仍然能够对这些模糊值进行计算操作。类似于哈希函数,在计算后很难回到原始输入。
同态加密
这正是同态加密的设计目的。即,它允许加密一个值并能够对这种加密进行算术操作。有多种方法可以实现加密的同态属性,我们将简要介绍一种简单的方法。
总体思路是我们选择一个基数(基数需要具有某些属性)自然数 g(比如 5),并通过将 g 提升到该值的幂来加密一个值。例如,如果我们想加密数字 3:
其中 125 是 3 的加密。如果我们想将这个加密的数字乘以 2,我们将其提升到 2 的幂:
我们能够将一个未知值乘以 2 并保持其加密状态。我们还可以通过乘法来相加两个加密值,例如,3 + 2:
同样,我们可以通过除法来减去加密数字,例如,5 – 3:
然而,由于基数 5 是公开的,很容易通过将加密值除以 5 直到结果为 1 来回到秘密数字。步骤数就是秘密数字。
模运算
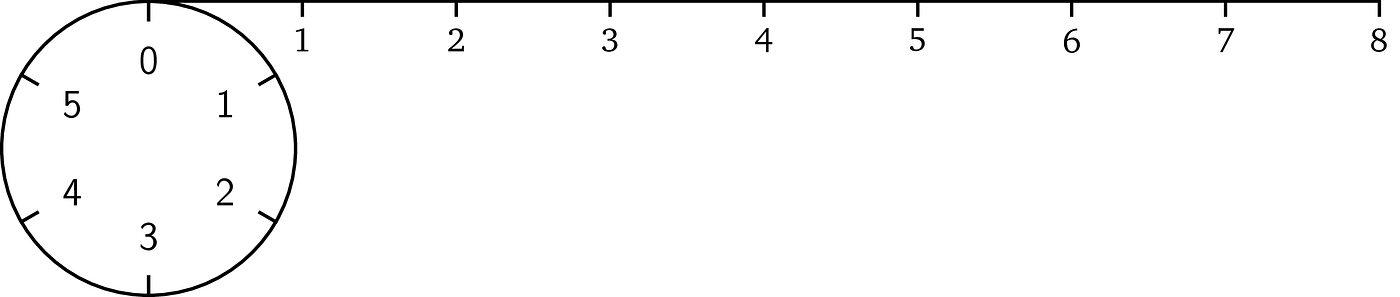
这就是模运算的用武之地。模运算的思想如下:我们声明只选择前 n 个自然数,即 0, 1, …, n – 1 来工作,如果任何给定的整数超出这个范围,我们将其“包裹”起来。例如,让我们选择前六个数字。为了说明这一点,考虑一个有六个等单位刻度的圆;这是我们的范围(通常称为有限域)。
现在让我们看看数字八会落在哪里。作为类比,我们可以将其视为一根长度为八个单位的绳子:
如果我们将绳子连接到圆的起点
并开始将绳子绕在它周围,经过一圈后我们仍然有一部分绳子剩下:
因此,如果我们继续这个过程,绳子将正好在刻度#2 处结束。
这是模运算的结果。不管绳子有多长,它总会停在圆的某个刻度上。因此,模运算将其保持在某个范围内(在这种情况下是 0 到 5)。15 单位的绳子将停在 3,即 6 + 6 + 3(两圈完整的圆加上 3 个单位的剩余)。负数的工作方式相同,唯一的区别是我们将其包裹在相反的方向,对于–8,结果将是 4。
此外,我们可以执行算术运算,结果将始终在 n 个数字的范围内。我们将使用“mod n”的符号来表示数字范围。例如:
此外,最重要的属性是操作的顺序无关紧要,例如,我们可以先执行所有操作然后应用模运算,或者在每次操作后应用模运算。例如(2 × 4 – 1) × 3 = 3 (mod 6)等价于:
那么这有什么用呢?事实证明,如果我们使用模运算,拥有操作的结果很难回到原始数字,因为许多不同的组合将具有相同的结果:
没有模运算,结果的大小会给出其解决方案的线索。这条信息被隐藏了,同时保留了常见的算术属性。
强同态加密
如果我们回到同态加密并使用模运算,例如模 7,我们将得到:
不同的指数将具有相同的结果:
这使得找到指数变得困难。事实上,如果模数足够大,几乎不可能做到这一点,现代密码学的很大一部分基于这个问题的“难度”。
所有方案的同态属性在模运算领域中都得以保留:
注意:模除法有点复杂,超出了本文的范围。
让我们明确说明加密函数:
其中 v 是我们要加密的值。
备注 3.2 这种同态加密方案有其局限性,虽然我们可以将加密值乘以未加密值,但我们不能将两个加密值相乘(和相除),也不能将加密值取幂。虽然从第一印象来看这很不幸,但这些属性将成为 zk-SNARK 的基石。这些局限性将在“加密值的乘法”一节中解决。
加密多项式
有了这些工具,我们现在可以用加密的随机值 x 来评估多项式,并相应地修改 零知识 协议。
让我们看看如何评估多项式 $p(x) = x³ – 3x² + 2x$。正如我们之前所说,了解一个多项式就是了解它的系数,在这种情况下,这些系数是:1, –3, 2。由于同态加密不允许对加密值取幂,我们必须得到从 1 到 3 的 x 的幂的加密值:$E(x) , E(x²), E(x³)$,以便我们可以如下评估加密多项式:
通过这样的操作结果,我们在某个我们未知的 x 处得到了多项式的加密评估。这是一个非常强大的机制,由于同态属性,相同多项式的加密评估在加密空间中总是相同的。
我们现在可以更新协议的先前版本,对于一个度为 d 的多项式:
注意:因为证明者对 s 一无所知,所以很难提出不合法但仍然匹配的评估。虽然在这种协议中证明者的灵活性有限,但他仍然可以使用任何其他方法来伪造证明,而不实际使用提供的 s 的幂的加密。例如,如果证明者声称仅使用 s³ 和 s¹ 的幂来获得一个满意的多项式,这是在当前协议中无法验证的。
限制多项式
对多项式的了解就是对其系数 $c₀,c₁,…,cᵢ$ 的了解,我们在协议中“分配”这些系数的方式是通过对秘密值 s 的相应加密幂进行指数运算。我们确实已经限制了证明者在选择 s 的加密幂时的选择,但这种限制并未强制执行,例如,可以使用任何可能的方法找到满足方程的任意值$zₚ$和$zₕ$,
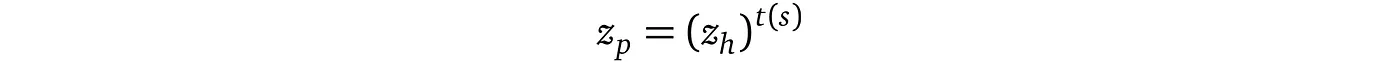
并将其提供给验证者,而不是 gᵖ 和 gʰ。这就是为什么验证者需要证明只使用了 s 的加密幂,而没有其他东西。
让我们考虑一个具有一个变量和一个系数的 1 次多项式的基本示例 f(x) = c ⋅ x,相应地提供 s 的加密 E(s) = gˢ。我们要确保的是仅对 s 的加密,即 gˢ ,进行了同态“乘法”运算,并且没有其他东西。因此,结果必须始终是以下形式(对于某个任意 c):
一种方法是要求对另一个“移位”的加密值执行相同的操作,同时对原始值执行操作,作为“校验和”的算术类比,确保结果是原始值的指数运算。
这是通过指数知识假设(KEA)实现的,该假设在[Dam91]中引入,更准确地说(注意 a 和 α(alpha)之间的区别):
a) Alice 有一个值 a,她希望 Bob 将其指数化为任何幂(其中 a 是所用有限域群的生成元),唯一的要求是只能对这个 a 进行指数运算,为了确保这一点,她:
b) 因为 Bob 无法从元组( a,a′ )中提取 α,除非通过暴力破解,这是不可行的,因此推测 Bob 生成有效响应的唯一方法是通过以下过程:
c) 拥有响应和_α_后,Alice 检查等式:
结论:
- Bob 对元组的两个值应用了相同的指数(即c)
- Bob 只能使用 Alice 的原始元组来保持 α 关系
- Bob 知道应用的指数 c,因为生成有效(b,b′)的唯一方法是使用相同的指数
- Alice 没有学到 c,因为同样的原因 Bob 无法知道 α*。
尽管 c 是加密的,但其可能值的范围可能不足以保持零知识属性,这将在“零知识”部分中解决。
最终,这种协议向 Alice 提供了 Bob 确实对 a 进行了某个已知值的指数运算的证明,并且他不能进行任何其他操作,例如乘法、加法,因为这会抹去 α 移位关系。
在同态加密上下文中,指数运算是加密值的乘法。我们可以在具有简单单系数多项式 f(x) = c ⋅ x 的情况下应用相同的构造:
- 验证者选择随机 s,α 并提供对幂为 1 的 x = s 及其“移位”的评估:
- 证明者应用系数 c:
- 验证者检查:
这种构造限制了证明者只能使用提供的加密 s,因此证明者只能将系数 c 分配给验证者提供的多项式。我们现在可以将这种单项式方法扩展到多项式,因为每项的系数分配是分别计算的,然后同态“相加”(这种方法由 Jens Groth 在[Gro10]中引入)。因此,如果证明者给出了_s_的加密指数及其移位值,他可以评估原始和移位多项式,其中相同的检查必须成立。特别是,对于一个度为_d_的多项式:
对于我们之前的多项式示例 $p(x) = x³ – 3x² + 2x $,这将是:
现在我们可以确定证明者没有使用验证者提供的多项式以外的任何东西,因为没有其他方法可以保持_α_移位关系。此外,如果验证者希望确保在证明者的多项式中排除某些 s 的幂,例如 j ,他将不提供加密及其移位:
与我们开始时相比,我们现在有了一个健壮的协议。然而,尽管有加密,但在零知识属性方面仍然存在一个显著缺陷:虽然理论上多项式系数$cᵢ$可以有广泛的值范围,但实际上可能非常有限(在前面的示例中为 6),这意味着验证者可以通过暴力破解有限的系数组合范围,直到结果等于证明者的答案。例如,如果我们考虑每个系数的 100 个值范围,2 次多项式将总共具有 100 万个不同的组合,考虑到暴力破解将需要不到一百万次迭代。此外,安全协议即使在只有一个系数且其值为 1 的情况下也应是安全的。
零知识
因为验证者只能从证明者发送数据中提取未知多项式 p(x) 的知识,让我们考虑这些提供的值(证明):
它们参与以下检查:
问题是我们如何改变证明,使检查仍然成立,但无法提取任何知识?一个答案可以从前一节中得出:我们可以通过某个随机数 δ(delta)“移位”这些值,例如( $gᵖ )ᵟ$。现在,为了提取知识,首先需要找到 δ,这被认为是不可行的。此外,这种随机化在统计上与随机不可区分。
为了保持关系,让我们检查验证者的检查。每个方程的两边都有证明者的一个值。因此,如果我们用相同的 δ “移位”它们,方程必须保持平衡。
具体来说,证明者采样一个随机 δ 并用它对他的证明值进行指数运算
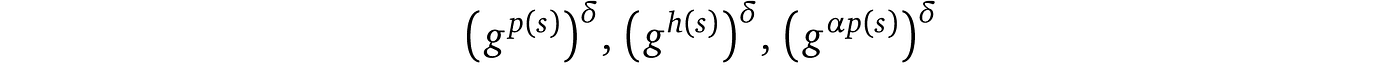
合并后我们可以观察到检查仍然成立:
注意:零知识是如何轻松地融入构造中的,这通常被称为“免费”的零知识。
参考文献
[Pik14] — Scott Pike. Dividing by a Polynomial. 2014. url: http://www.mesacc.edu/~scotz47781/mat120/notes/divide_poly/long_division/long_division.html(访问于 2018–05–01)
[Dam91] — Ivan Damgård. “Towards practical public key systems secure against chosen ciphertext attacks”. In: Annual International Cryptology Conference. Springer. 1991, pp. 445–456.
[Gro10] — Jens Groth. “Short pairing-based non-interactive zero-knowledge arguments”. In: International Conference on the Theory and Application of Cryptology and Information Security. Springer. 2010, pp. 321–340.
- ZK Mesh:2025年12月回顾 718 浏览
- ZK Mesh:2025年9月回顾 1345 浏览
- 应用 ZK 解数独,无需泄露答案 1787 浏览
- ZK Mesh:2025年7月回顾 1397 浏览
- Labrador:后量子 ZK 证明的新纪元 1407 浏览
- 我们来了解一下拉布拉多协议 1260 浏览
- Web 3 的世界近在咫尺 - 浏览器中的 ZKP 1766 浏览
- 密码学 - 斯巴达 1753 浏览
- ZK论文解读--SoK: Understanding zk-SNARKs: The Gap Between Research and Practice 1953 浏览
- 密码学基础:零知识证明(第三部分) 4073 浏览
- 为我们其他人准备的 BN254 2284 浏览
- gnark中Groth16证明的两个漏洞 2186 浏览