密码学基础三 门限共享密码算法
- Leo
- 发布于 2024-09-15 11:09
- 阅读 4293
概念门限秘密共享是一种密码学技术,将秘密S分割为n个部分,并将这些部分分发给n个参与者。所谓门限,是在分割这些秘密的时候,设置一个大小位于1和n之间的k值,使得给定任意k−1个或更少的秘密份额,都不能够计算得到秘密S的任何信息;当给定任意k个或更多的秘密
概念
门限秘密共享是一种密码学技术,将秘密 S 分割为 n 个部分,并将这些部分分发给 n 个参与者。所谓门限,是在分割这些秘密的时候,设置一个大小位于 1 和 n 之间的 k 值,使得给定任意 k−1 个或更少的秘密份额,都不能够计算得到秘密 S 的任何信息;当给定任意 k 个或更多的秘密份额的时候,就能够计算得到秘密 S。这被称为 (k,n) 门限秘密共享方案。这意味着这 n 个参与者中最多 k−1 个参与者泄露了他们的秘密份额,秘密 S 仍然是安全的。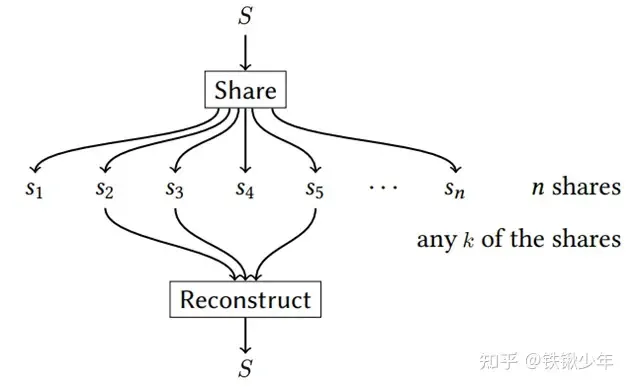
举一个直观的案例,如下图:
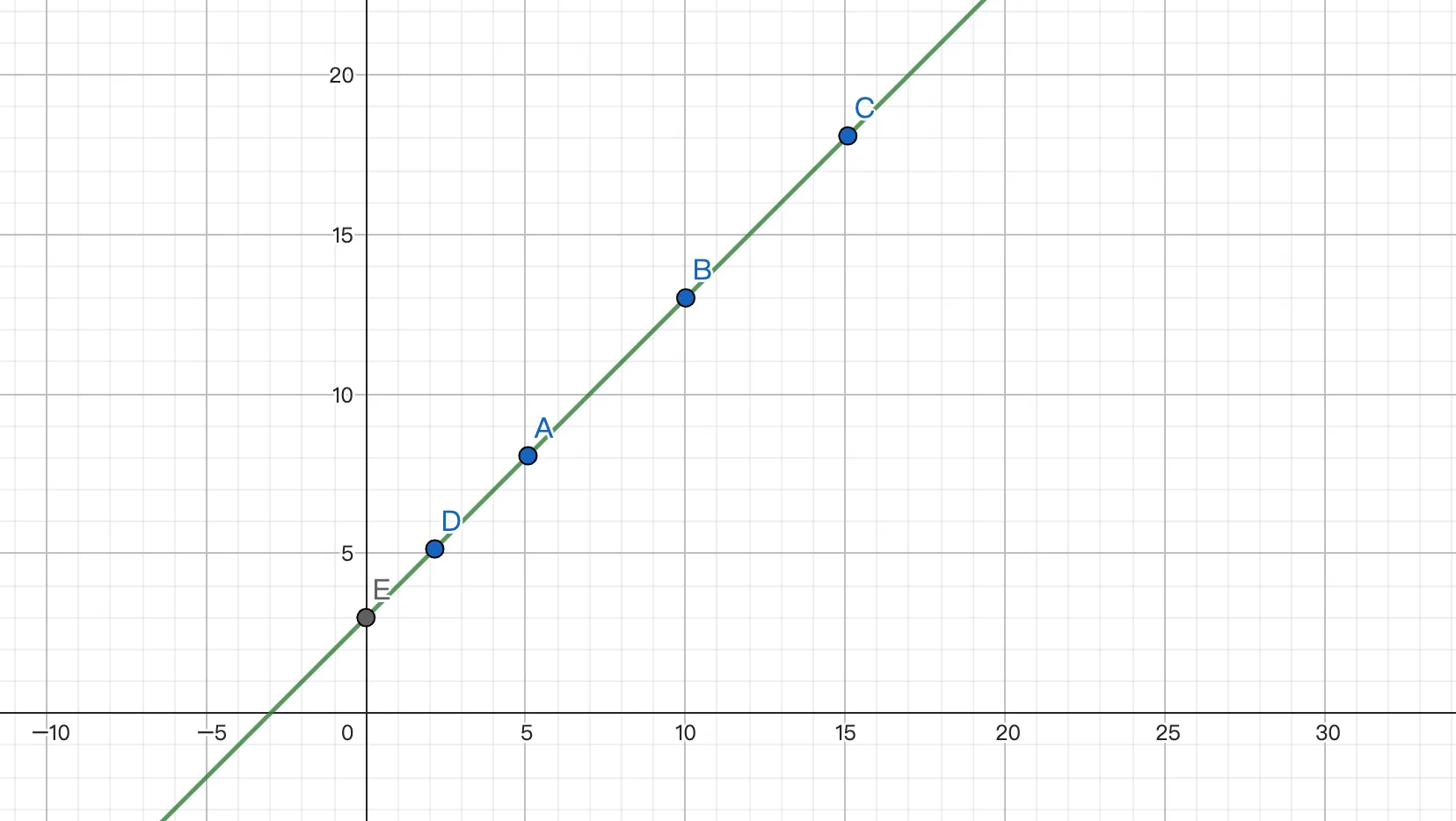
假设E即为共享秘密,A,B,C,D 四个点分别是一个子密钥,需要任意两个子密钥就能得到真正的结果E。按照图示,我们可以通过两个坐标点位,获得一元一次方程的公式,可以反向推导出最终值E的结果。(当然,上述例子只是一个引子,实际的秘密共享算法并不会如此简单,比如:Shamir秘密共享)
Shamir秘密共享
Shamir 秘密共享(Shamir's Secret Sharing)是一种密码学算法,用于将一个秘密(如密码、密钥等)分割成多个部分(称为份额),并且只有当收集到足够多的份额时,才能恢复该秘密。该算法由以色列密码学家 Adi Shamir 于 1979 年提出,是实现密钥分发和分布式存储的经典方法之一。 Shamir 秘密共享 和核心数学原理是拉格朗日插值算法,它使用了一个由多项式生成的函数,其中秘密作为多项式的常数项,而每个份额则是该多项式在不同点上的值。通过至少一定数量的份额可以重建这个多项式。
工作原理
一 选择多项式 (x)=S+a1x+a2x^2+⋯+at−1x^t−1。 其中S是常数,即要共享的秘密
二 生成份额 生成 n 个不同的非零值 x_1, x_2, ..., x_n,并计算对应的 y 值,即 f(x_1), f(x_2), ..., f(x_n),每个x对应一个份额,并将这些份额分发给不同的参与者
三 恢复秘密 至少有 t 个份额时,可以使用拉格朗日插值法重建多项式 f(x),从而求出常数项 S
Java 算法实现
public class ShamirSecretSharing {
// 分享份额类,包含X和Y
public static class Share {
public final int x;
public final BigInteger y;
public Share(int x, BigInteger y) {
this.x = x;
this.y = y;
}
@Override
public String toString() {
return "Share{" + "x=" + x + ", y=" + y + '}';
}
}
private final SecureRandom random = new SecureRandom();
private final int threshold; // 至少需要的份额数量 t
private final int numShares; // 份额总数 n
private final BigInteger prime; // 大素数,保证结果不溢出
public ShamirSecretSharing(int threshold, int numShares, BigInteger prime) {
this.threshold = threshold;
this.numShares = numShares;
this.prime = prime;
}
// 生成秘密的份额
public List<Share> split(BigInteger secret) {
// 随机生成 (t-1) 个系数
BigInteger[] coefficients = new BigInteger[threshold - 1];
for (int i = 0; i < threshold - 1; i++) {
coefficients[i] = new BigInteger(prime.bitLength(), random).mod(prime);
}
// 生成 n 个份额
List<Share> shares = new ArrayList<>();
for (int i = 1; i <= numShares; i++) {
BigInteger x = BigInteger.valueOf(i);
BigInteger y = evaluatePolynomial(secret, coefficients, x);
shares.add(new Share(i, y));
}
return shares;
}
// 恢复秘密
public BigInteger combine(List<Share> shares) {
BigInteger secret = BigInteger.ZERO;
for (int i = 0; i < shares.size(); i++) {
Share si = shares.get(i);
BigInteger numerator = BigInteger.ONE;
BigInteger denominator = BigInteger.ONE;
for (int j = 0; j < shares.size(); j++) {
if (i != j) {
Share sj = shares.get(j);
numerator = numerator.multiply(BigInteger.valueOf(-sj.x)).mod(prime);
denominator = denominator.multiply(BigInteger.valueOf(si.x - sj.x)).mod(prime);
}
}
BigInteger value = si.y.multiply(numerator).multiply(denominator.modInverse(prime)).mod(prime);
secret = secret.add(value).mod(prime);
}
return secret;
}
// 计算多项式的值 y = secret + a1*x + a2*x^2 + ... + at-1*x^(t-1)
private BigInteger evaluatePolynomial(BigInteger secret, BigInteger[] coefficients, BigInteger x) {
BigInteger result = secret;
for (int i = 0; i < coefficients.length; i++) {
result = result.add(coefficients[i].multiply(x.pow(i + 1))).mod(prime);
}
return result;
}
public static void main(String[] args) {
// 大素数 prime
BigInteger prime = new BigInteger("208351617316091241234326746312124448251235562226470491514186331217050270460481");
// 假设我们要分享的秘密是 123456789
BigInteger secret = new BigInteger("123456789");
// 创建 ShamirSecretSharing 实例,阈值为 3,总份额为 5
ShamirSecretSharing sss = new ShamirSecretSharing(3, 5, prime);
// 生成 5 份份额,至少需要 3 份来恢复秘密
List<Share> shares = sss.split(secret);
System.out.println("生成的份额:");
for (Share share : shares) {
System.out.println(share);
}
// 恢复秘密,选取前 3 份
List<Share> selectedShares = shares.subList(0, 3);
BigInteger recoveredSecret = sss.combine(selectedShares);
System.out.println("恢复的秘密: " + recoveredSecret);
}
}方法说明
split() 方法:将秘密分割成多个份额,每个份额包含一个 x 值和对应的多项式计算得到的 y 值。 combine() 方法:从多个份额中恢复秘密,通过拉格朗日插值法进行多项式的重建。 evaluatePolynomial() 方法根据秘密和随机生成的多项式系数,计算每个份额对应的值。
prime 的作用
使用一个大素数(prime)的核心作用是为了在有限域(有限个元素的数学结构)中进行计算。 它的核心作用是 一 防止溢出 通过在一个有限域内(即以一个大素数为模)进行运算,可以确保所有计算的结果都被限制在这个素数的范围内 二 增加安全性 有限域的使用使得攻击者不能轻易通过少量份额来推断秘密。如果不使用大素数并且允许无限制的大数运算,攻击者可能利用这些信息通过一些数学攻击恢复原始的秘密。 三 确保每个份额是唯一的 大素数还确保了在不同的 x 值对应的份额是唯一的。由于所有计算都在模素数的范围内完成,每个份额的 y 值是通过该 x 值的唯一多项式值来计算的。这保证了每个份额都具有独立的数学结构,避免了份额之间的重合或冲突。
参考文献 https://zhuanlan.zhihu.com/p/710732805 https://github.com/the-web3/cryptography/blob/master/share/README.md
- 以太坊协议研究学习小组 - 2026 启动 128 浏览
- 神奇的 Zig、C 和 OpenSSL 153 浏览
- Shamir份额的魔力:BLS门限签名 408 浏览
- zkMesh:2026年1月回顾 416 浏览
- FRI (and friends) 使用 Lean4 形式化验证 FRI(及相关内容) 406 浏览
- ZK 编年史:电路(第二部分) 406 浏览
- 有限域之美与力量 (以及 Zig) 499 浏览
- 扳手攻击:发生与预防 531 浏览
- zkEVM 安全性概览 602 浏览
- 基于哈希函数的签名(三):多次签名 674 浏览
- 基于哈希函数的签名(二):少量次数签名 844 浏览
- Zig 签名(Ed25519 和 ECDSA) 1187 浏览

