【Uniswap V2】| 回顾 Uniswap V2 之详解手续费
- 0xE
- 发布于 2024-10-09 17:47
- 阅读 4859
使用多种推导方式,一篇文章,讲清交易费、协议费。
在 Uniswap V2 中,手续费分为两种。一是交易费,每笔交易的 0.3% 将分配给流动性提供者;另一种是可选的协议费,该费用从交易费中提取 1/6,归 Uniswap 所有。当开启协议费,用户在 Swap 时仍然只需支付 0.3% 的手续费,只是一部分给流动性提供者,一部分给协议。
流动性可以通过池中代币余额的乘积平方根来表示,通常用 $\sqrt{k}$ 表示,其中 $k = x \times y$。$x$ 和 $y$ 分别代表两种代币的储备量。为了简化叙述,本文将流动性记作 $l$,即 $l = \sqrt{k} = \sqrt{x \times y}$。
什么时候收手续费
交易费:
每次用户进行 Swap 操作时,合约会从交易中扣除一部分资金,沉淀在流动性池中,作为交易费。随着交易次数的增加,池中的两种代币储备量会逐渐增多,而流动性池的 LP 代币总量保持不变,用户持有的 LP 代币数量也不变。由于池中的代币储备增加,当流动性提供者移除流动性时,相同数量的 LP 代币将对应更多的代币储备,流动性提供者因此获得手续费。
协议费:
通常来说,协议费可以在每笔交易时直接扣除一部分代币,并转移给协议费接收者。但这样设计会增加 gas 消耗。
在 Uniswap 中,协议费的收取发生在用户增加或移除流动性(即 mint 和 burn 操作)时,具体方式是增发 LP 代币给协议费接收者。例如,当某用户移除流动性时,合约首先会 mint 出需要作为协议费的 LP 代币并转移给协议费接收者,此时 LP 代币的总量增加。然后再算这个用户移除流动性可以获得的代币数量,用户实际收到的代币会比未开启协议费时要少,这相当于扣除了一部分代币作为协议费。
那么,这个协议费对应的 LP 数量的计算就是我们这篇文章介绍的重点。
协议费的计算公式推导
我们将介绍两种推导方式,帮助大家更好地理解。
首先,回顾添加流动性时,给用户 mint LP 代币的计算公式。为简化起见,我们不考虑首次添加流动性以及取最小值的情况:
$\frac{\text{liquidity}}{\text{totalSupply}} = \frac{\text{amount}}{\text{reserve}}$
其中:
- $\text{liquidity}$:需要计算的 LP 代币数量。
- $\text{totalSupply}$:原有的 LP 代币总数量。
- $\text{amount}$:此次添加的代币数量。
- $\text{reserve}$:原有的代币储备量。
类似地,我们可以参考这个公式,逐步推导出需要给协议费接收者 mint 的 LP 代币数量,记为 $S_m$。
我们将原有的 LP 代币总数量记为 $S_1$,这样命名是为了与白皮书中的公式保持一致,表示 $t_1$ 时刻的 LP 总数量。
本次添加的流动性数量可以表示为 $\frac{1}{6} \times (l_2 - l_1)$,其中 $l_1$ 表示 $t_1$ 时刻的流动性数量,$l_2$ 表示累积完手续费后的流动性数量,乘以 $\frac{1}{6}$ 表示分配给协议费的比例。
值得注意的是,并不是把 $l_1$ 代入公式中,因为有 $\frac{5}{6}$ 的手续费是分给流动性提供者的,这部分不参与 mint LP 代币,而是沉淀在池子中用来给用户移除流动性的时候给交易费的。正确的表达应该是:$l_1 + \frac{5}{6} \times (l_2 - l_1)$。
结合下图,能帮助大家更直观地理解这个过程。
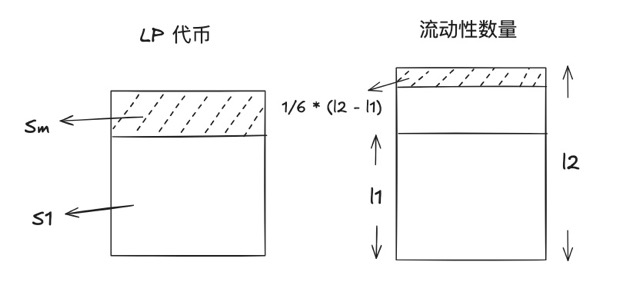
所以,我们能得出公式:
$\frac{S_m}{S_1} = \frac{\frac{1}{6} \times (l_2 - l_1)}{l_1 + \frac{5}{6} \times (l_2 - l_1)}$
推导出最终的结果为:
$S_m = \frac{l_2 - l_1}{5 \cdot l_2 + l_1} \cdot S_1$
第二种推导方式来自白皮书中的公式。

公式(4)$f_{1,2} = 1 - \frac{l_1}{l_2} = \frac{l_2 - l_1}{l_2}$的意思是 $l_1$ 相对于 $l_2$ 的缺少部分(即增长部分)占总量的百分比。
表达式 $\phi \cdot f_{1,2}$ 就相当于之前给出的图中阴影部分占总量的百分比。
同样地,$\frac{S_m}{S_m + S_1}$ 的意思是 $S_1$ 相对于 $S_m + S_1$ 的缺少部分(即增长部分$S_m$)占总量的百分比。
LP 代币数量和流动性数量两者缺少部分占总量百分比是一样的,于是有了白皮书中的推导过程。
和第一种推导方式不同的是,先分别列出增长部分在总体中的占比,而第一种是直接按照比例式子。
我们还可以这样理解,假设 $S{2}$ 是 $t{2}$ 时间点 LP 的总数量,那么公式还可以转变成$\frac{S{2} - S{1}}{S_{2}} = \frac{1}{6} \cdot \frac{l_2 - l_1}{l_2}$。如下图所示。
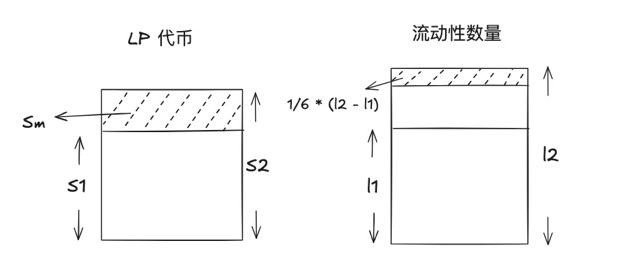
可以求出 $S_2 = \frac{6 \cdot l_2}{5 \cdot l_2 + l_1} \times S_1$
那么 $S_m = S_2 - S_1 = \frac{6 \cdot l_2}{5 \cdot l_2 + l_1} \times S_1 - S_1 = \frac{l_2 - l_1}{5 \cdot l_2 + l_1} \cdot S_1$
_mintFee() 代码
在 mint(address to) 和 burn(address to) 函数中有调用 _mintFee() 的部分,来结算协议费。当协议费开启,每次 mint 或者 burn 都会更新 kLast。
...
bool feeOn = _mintFee(_reserve0, _reserve1);
...
if (feeOn) kLast = uint(reserve0).mul(reserve1); // reserve0 and reserve1 are up-to-date
function _mintFee(uint112 _reserve0, uint112 _reserve1) private returns (bool feeOn) {
address feeTo = IUniswapV2Factory(factory).feeTo();
feeOn = feeTo != address(0);
uint _kLast = kLast; // gas savings
if (feeOn) {
if (_kLast != 0) {
uint rootK = Math.sqrt(uint(_reserve0).mul(_reserve1));
uint rootKLast = Math.sqrt(_kLast);
if (rootK > rootKLast) {
uint numerator = totalSupply.mul(rootK.sub(rootKLast));
uint denominator = rootK.mul(5).add(rootKLast);
uint liquidity = numerator / denominator;
if (liquidity > 0) _mint(feeTo, liquidity);
}
}
} else if (_kLast != 0) {
kLast = 0;
}
}代码和公式的对应关系为:
$S_m = \frac{l_2 - l_1}{5 \cdot l_2 + l_1} \cdot S_1$
rootK = $\sqrt{k_2} = l_2$
rootKLast = $\sqrt{k_1} = l_1$
totalSupply = $S_1$
numerator = $(l_2 -l_1) \cdot S_1$ 式子的分子部分。
denominator = $5 \cdot l_2 + l_1$ 式子的分母部分。
liquidity = $S_m$
判断是否发协议费的过程为:
利用工厂合约中的 feeTo 地址是否为空来判断协议费是否开启。如果之前开启过协议费,而这次交易的时候关闭了,需要把之前不为 0 的 kLast 重置为 0。
如果协议费是开启的,获取上次的 kLast,如果 kLast 为 0,说明是刚刚开启,此时如果计算,那 $l_1 = 0$,但是实际的之前的流动性一般不为 0,所以需要更新一次 kLast 再计算协议费发放。
当上次的 kLast 不等于 0,那么需要看流动性是否增长了,即 $l_2 > l_1$,只有流动性数量增长了,才需要发放协议费。
- 原创
- 学分: 42
- 分类: Solidity
- 标签: Solidity DeFi Uniswap V2
- 来自 Tomasz 的更新 124 浏览
- DAO2.0 从理论到代码:新一代去中心化治理实战 187 浏览
- 拒绝 DAO 落地难!用代码把「去中心化治理」写进合约:DAO 全流程开发实录 308 浏览
- “夺旗”竞赛继续! 223 浏览
- AI 正热,加密货币遇冷,那又如何? 346 浏览
- Polymarket交易手册 315 浏览

