zkMIPS解读
【zkMIPS系列】FRI预备知识
- ZKM
- 发布于 2024-11-01 16:35
- 阅读 3343
FRI预备知识:多项式的阶、群与有限域、Reed-Solomon码、FRI动机、密码工具Merkle树
预备知识
- 多项式和阶 1.1 多项式基本概念及其在密码学中的应用 1.2 低阶多项式的重要性及其在证明系统中的意义
- 群与有限域 2.1 群和有限域 2.2 子群和陪集 2.3 循环群和单位根 (root of unity) 2.4 FRI中大素数的选取
- Reed-Solomon 码 3.1 什么是 RS 码及其在多项式承诺中的角色 3.2 RS码的性质
- FRI 的动机 4.1 为什么需要快速的低阶测试?传统方法的挑战与局限
- 密码学工具 5.1 Merkle Tree和Merkle Proof
1. 多项式和阶
1.1 多项式基本概念及其在密码学中的应用
多项式是代数中的基本概念,表示为变量和系数的线性组合,记为 $$ p(x)=a_0+a_1 x+a_2 x^2+⋯+a_d x^d $$ 其中 $a_i$是系数,$d$是多项式的阶。多项式广泛应用于数学、物理学和工程学,尤其在密码学中扮演着核心角色。多项式的可组合性、简单的代数性质使其成为多种加密技术和协议的基础。 在密码学中,特别是在编码理论、零知识证明和加密算法中,多项式具有关键作用。例如,在Reed-Solomon 编码中,多项式用于将数据编码为码字,用于错误检测和纠正。多项式的代数性质能够保证数据在传输过程中即使受到噪声影响,仍然可以通过解码过程恢复原始数据,这种可靠性对于确保信息传输的完整性至关重要。
此外,在零知识证明的预处理阶段,通常需要将算术电路将其等价规约到多项式的表示,并通过构建PIOP交互式证明的方式,对多项式进行算术运算,从而证明特定等式成立。多项式的可操作性和复杂性确保了密码系统的强度,同时仍然允许高效的计算和验证。
1.2 低阶多项式的重要性及其在证明系统中的意义
在零知识证明和可验证计算等密码学领域,低阶多项式的作用十分显著。低阶多项式的特点是计算简单且验证速度快,这使得它们在证明系统中具有极高的实用性。证明系统的一个重要目标是快速验证复杂计算的正确性,而低阶多项式能够在这一过程中显著降低计算成本。
例如,在 zk-SNARK (零知识简洁非互动知识论证)中,低阶多项式用于生成和验证证明,这些多项式的低度数确保了验证者可以在不暴露原始数据的情况下高效验证计算结果,这种低度数特性不仅提高了验证的速度,还减少了验证过程中的资源消耗。
此外,低阶多项式在 Reed-Solomon 编码 的低度数测试(Low-Degree Test)中同样重要,通过验证多项式是否保持低阶,可以判断数据的完整性,并有效检测和纠正传输错误。低阶多项式的鲁棒性和可靠性,使得低阶多项式成为证明系统中不可或缺的工具。
总的来说,低阶多项式的简洁性和有效性使其成为密码学中构建安全、高效证明系统的关键要素。通过利用低阶多项式,证明系统能够在确保安全性的同时显著提高计算效率,降低系统复杂性,从而在实际应用中表现出优越的性能。
2. 群与有限域
群是一个集合,集合中每个元素之间满足一定规定的运算,比如在数论中常见的mod p可以抽象为一个有限域$F_p$,其中的元素是不超过$p-1$的非负整数$0,...,(p-1)$,本节将重点介绍群和有限域的概念。
2.1 群和有限域。
群 是一个代数结构,由一个集合和一个在该集合上的二元运算构成。一个群 $G$ 需要满足以下四个性质:
- 封闭性(Closure): 对于群中的任意两个元素 $a, b \in G$,运算结果 $a \cdot b$ 也属于 $G$。
- 结合性(Associativity): 对于任意 $a, b, c \in G$,有 $(a \cdot b) \cdot c = a \cdot (b \cdot c)$。
- 单位元(Identity element): 存在一个单位元 $e \in G$,使得对于任意 $a \in G$,有 $a \cdot e = e \cdot a = a$。
- 逆元(Inverse element): 对于任意 $a \in G$,存在一个逆元 $a^{-1} \in G$,使得 $a \cdot a^{-1} = a^{-1} \cdot a = e$。
示例:模 17 群 (F_17)
考虑集合 $\mathbb{Z}{17}^* = { 1, 2, 3, \dots, 16 }$ 及其乘法运算。对于任意两个元素 $a, b \in \mathbb{Z}{17}^$,运算 $a \cdot b \mod 17$ 仍然属于 $\mathbb{Z}_{17}^$。这个集合在乘法下构成一个群,其单位元为 1,逆元为乘法逆元。
有限域 是具有有限个元素的域,通常记为 $\mathbb{F}_q$,其中 $q$ 是一个素数或素数的幂次。在有限域中,加法和乘法分别构成两个群。
示例:域 $\mathbb{F}_{17}$
考虑有限域 $\mathbb{F}_{17} = { 0, 1, 2, \dots, 16 }$。在该域中,元素之间的加法和乘法分别构成群。例如,5 在乘法群中的逆元是 7,因为 $5 \times 7 \equiv 1 \mod 17$。
2.2 子群和陪集
子群 是一个包含在群中的子集,这个子集在群的运算下仍然构成一个群。设 $G$ 是一个群,$H$ 是 $G$ 的一个非空子集,如果 $H$ 对于 $G$ 的运算封闭并且自身满足群的四个性质,则称 $H$ 是 $G$ 的一个子群。
示例:模 17 乘法群的子群
考虑 $\mathbb{Z}_{17}^*$ 的一个子群 $H = { 1, 4, 16 }$,它在乘法下封闭且满足群的所有性质,因此是一个子群。
陪集 是子群在群中的一种分割方式。设 $H$ 是群 $G$ 的一个子群,对于 $G$ 中任意一个元素 $g$,左陪集 $gH$ 和右陪集 $Hg$ 分别定义为:
- 左陪集: $gH = { gh \mid h \in H }$
- 右陪集: $Hg = { hg \mid h \in H }$
示例:模 17 乘法群的陪集
对群 $\mathbb{Z}_{17}^*$ 中的元素 3 和子群 $H = { 1, 4, 16 }$,左陪集 $3H = { 3, 12, 14 }$,表示子群被划分为不同的等价类。
2.3 循环群和单位根 (root of unity)
循环群和单位根是零知识证明中常用的概念,其概念和具体示例如下: 循环群 是由单个元素生成的群。若存在一个元素 $g \in G$,使得 $G$ 中的每个元素都可以表示为 $g$ 的幂次形式,即 $G = { g^n \mid n \in \mathbb{Z} }$,则称 $G$ 为循环群。
示例:模 17 乘法群中的循环群
在 $\mathbb{Z}_{17}^*$ 中,元素 3 可以生成一个循环群: $$ { 3^0, 3^1, 3^2, \dots, 3^{15} } = { 1, 3, 9, 10, 13, 5, 15, 11, 16, 14, 8, 7, 4, 12, 2, 6 } $$
单位根 是复平面上某个特定次幂等于 1 的复数。设 $n$ 是正整数,单位根 $\omega$ 是满足 $\omega^n = 1$ 的复数。$n$ 次单位根的集合在复数乘法下构成一个循环群。
示例:$\mathbb{F}_{17}$ 中的单位根
在有限域 $\mathbb{F}{17}$ 中,元素 3 是一个原始根,即 $3^{16} \equiv 1 \mod 17$,并且 $3^k$ 产生了域 $\mathbb{F}{17}$ 中所有非零元素,构成一个循环群。 同时我们需要引入几个定理:
- 对于一个大素数阶的有限域$F_p$而言,必定存在若干个$n$阶循环群。其中,$n$可以被$p-1$整除;
- 阶为素数的群一定是循环群,故所有的$F_p$皆为循环群,且其中每个元素都是生成元;
- 因为循环群有着良好的性质,我们通常使用单位根来取代整数集,如通常使用一个含有单位根$g$的$n$阶循环子群${1, g, g^2, …, g^{n-1}}$,其中$g^n=1$,来代替集合${0, 1, 2, …, n-1}$。具体而言,循环群具有以下性质:
- 简化多项式运算 在 zkSNARKs 中,单位根尤其适用于快速傅里叶变换(FFT),可以极大地加速多项式的插值和求值。具体来说,如果使用单位根作为采样点,FFT 使得从系数形式转化为值形式,以及从值形式转化为系数形式,都可以在O(nlogn)内完成。
- 简化零点检测 对于零点检测而言,通常会使用一个prover polynomial除以一个vanishing polynomial得到一个商多项式来进行证明,采用单位根,则其对应的vanishing polynomial Z(X)可以被简化为X^n-1,极大的降低了计算开销。
2.4 FRI中大素数的选取
在FRI中,通常选取素数$p=2^{64}-2^{32}+1$,该类素数称为Goldilocks素数(Goldilocks Prime),如刚才所说,如果一个循环子群具有阶$n$(即子群中元素的个数为$n$),那么$n$一定满足$p-1$可以整除$n$。
对于$p=2^{64}-2^{32}+1$而言,$p-1=2^{64}-2^{32}$,那么一个循环子群可以具有阶$n=2, 2^2, 2^3, …, 2^{32}$,FRI可以在2的幂次方上运行low-degree test,正好和一个满的二叉树具有2的幂次方个叶节点相匹配。
3. Reed-Solomon 码
3.1 Reed-Solomon 码
Reed-Solomon (RS)编码是一类非二进制的线性纠错码,广泛应用于光盘、卫星通信、QR码、硬盘等领域,用于错误检测和纠正。给定一个大小为$n$的集合$ (n>d)$,对于一个阶为$d$的多项式p(X)进行运算,从而构造一个长度为$n (n>d) $的码字,其具体定义如下:
给定一个阶为d的多项式p(X)和一个大小为n的集合 $$ \Omega={\omega, \omega^2, \dots, \omega^n} $$ RS编码值为${p(\omega^i)}_{i\in{[n]}}$。
3.2RS编码性质
- 扩张系数:$n=q\cdot d$。 其中,$q(q>2)$称为扩张系数 (FRI blowup factor)。当扩张系数越大,则代表证明方需要提交更多的Merkle hash值和进行更多的运算,证明大小和运算时间都会上升,同时验证时间也会相应降低。
- 编码差异判断: 在 Reed-Solomon 编码中,判断两个多项式是否接近可以通过比较它们的编码来判断。如果两个多项式的 RS 编码在大多数点上生成相同的值,那么这两个多项式是相近的,可以认为两个多项式之间具有相似的阶。
- 线性码: RS是一类线性编码,任何线性码之间的线性组合仍然是线性码。若两个RS编码均对应低阶的多项式,那么其线性组合也对应一个低阶的多项式。
4. FRI 的动机
4.1 低阶测试
FRI主要用于检查一个给定的多项式f是否超过最大阶$d$,它使用RS的上述三大性质,将问题不断规约为一个给定的多项式$f_{fold}$是否超过最大阶$d/2$,最终规约到一个常数级别的检查问题。我们将在后续重点介绍FRI的执行流程和内部的基本原理。
5. 密码学工具
5.1 Merkle Tree和Merkle Proof
在FRI的运行过程中,证明方需要首先对一个多项式P进行承诺,在打开特定点的过程中,需要同步提交该点的Merkle路径作为Merkle Proof.
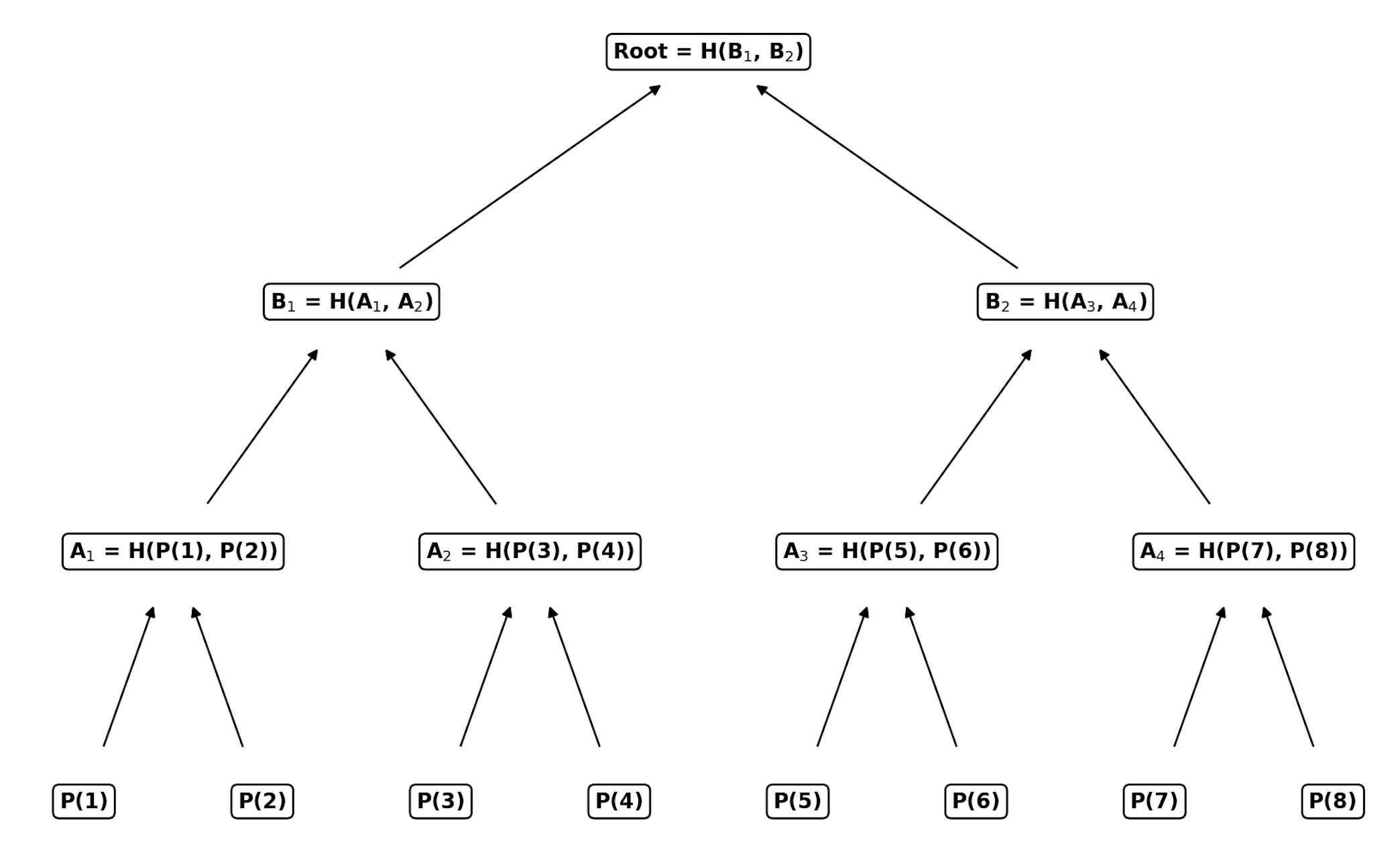
上图描述了一个多项式$P(X)$在$X={1,2,3,4,5,6,7,8}$上的Merkle commitment,Merkle树的建立过程是从叶节点开始,通常是左右两个子节点的哈希值作为上一层的根节点,不断递归,图中的Merkle建树的具体过程如下:
- 生成第一层中间节点
- 从 8 个叶子节点 $P(1), P(2), P(3), P(4), P(5), P(6), P(7), P(8)$ 开始。
- 对相邻的叶子节点进行哈希运算,生成四个中间节点:
- $A_1 = \mathsf{Hash}(P(1), P(2))$
- $A_2 = \mathsf{Hash}(P(3), P(4))$
- $A_3 = \mathsf{Hash}(P(5), P(6))$
- $A_4 = \mathsf{Hash}(P(7), P(8))$
- 生成第二层中间节点
- 对第一层的中间节点进行两两哈希运算,生成两个更高层次的节点:
- $B_1 = \mathsf{Hash}(A_1, A_2)$
- $B_2 = \mathsf{Hash}(A_3, A_4)$
- 生成根节点
- 最后,对第二层的两个节点进行哈希运算,生成根节点:
- $\text{Root} = \mathsf{Hash}(B_1, B_2)$
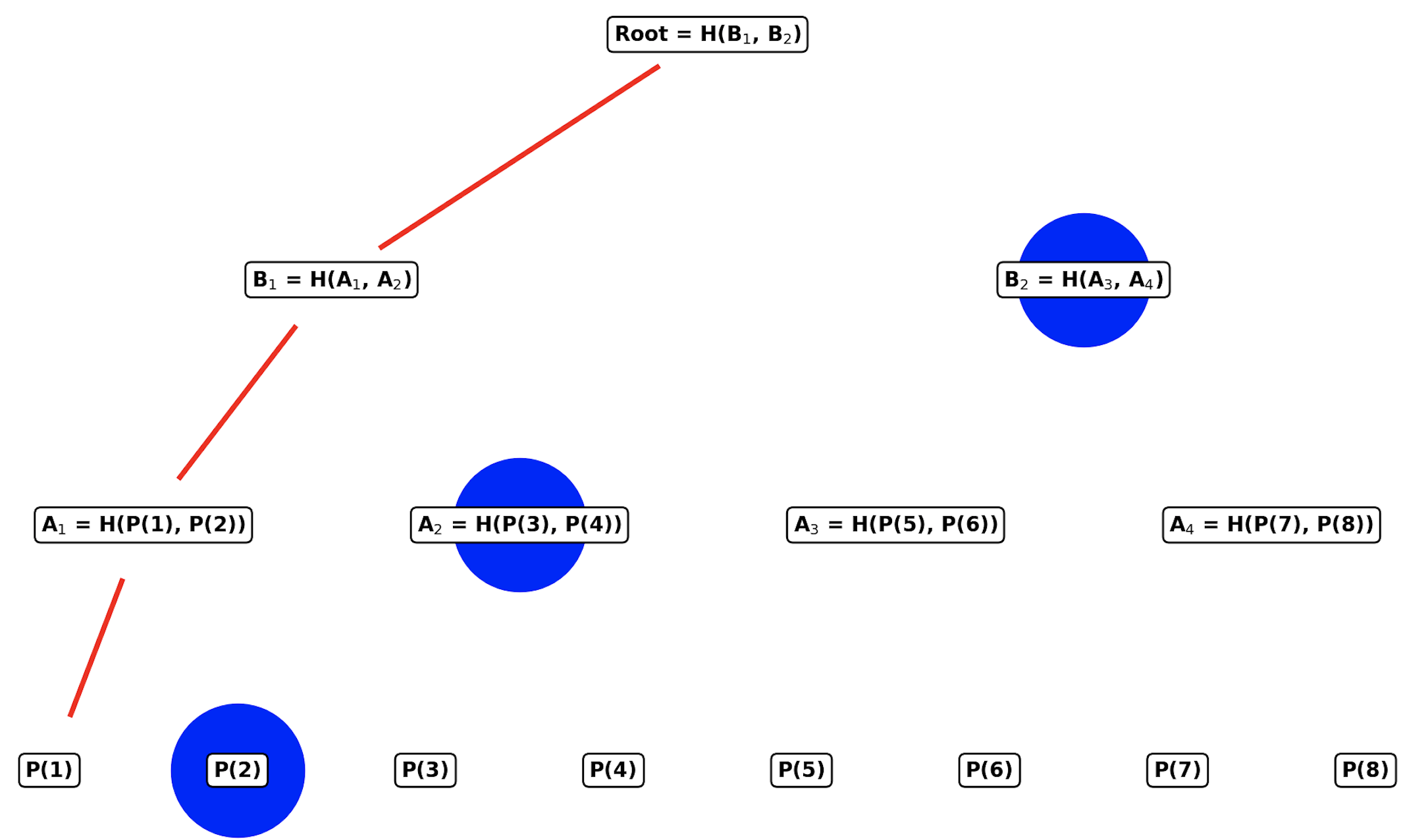 其中证明方保存整个树(包括每个根节点和叶子节点),而验证方仅保存根节点(本例为Root)。如果证明方需要打开Merkle树的叶子节点中的一个点,那么他就需要提交对应的Merkle path,对于上述例子而言,如果证明方想要打开$P(1)$,其生成Merkle proof的方式如下:
其中证明方保存整个树(包括每个根节点和叶子节点),而验证方仅保存根节点(本例为Root)。如果证明方需要打开Merkle树的叶子节点中的一个点,那么他就需要提交对应的Merkle path,对于上述例子而言,如果证明方想要打开$P(1)$,其生成Merkle proof的方式如下:
- 计算第一层哈希值
- 使用 $P(1)$ 和 $P(2)$ 计算 $A_1$:
- $A_1 = \mathsf{Hash}(P(1), P(2))$
- 在证明过程中,$P(2)$ 是需要提供的第一个节点。
- 计算第二层哈希值
- 使用 $A_1$ 和 $A_2$ 计算 $B_1$:
- $B_1 = \mathsf{Hash}(A_1, A_2)$
- 在证明过程中,$A_2$ 是需要提供的第二个节点。
- 计算根节点
- 使用 $B_1$ 和 $B_2$ 计算根节点:
- $\text{Root} = \mathsf{Hash}(B_1, B_2)$
- 在证明过程中,$B_2$ 是需要提供的第三个节点。
图中蓝色标出来的节点,是打开$P(1)$对应的Merkle proof,验证方仅需要对这些Merkle Proof重新调用哈希函数,并判断是否与Root相等,即可判断$P(1)$是否在Merkle树中。 Merkle Proof的主要优点在于:
- 计算开销小: 仅需要进行哈希函数等计算高效的操作;
- 证明规模小: 假设一个树中存储了$d$个叶节点,只需要提交规模为$\log d$的证明证据即可。
