零知识证明 - 从QSP到QAP
- Star Li
- 发布于 2019-05-07 15:10
- 阅读 28345
前一段时间,介绍了零知识证明的入门知识,通过QSP问题证明来验证另外一个NP问题的解。最近在看QAP问题相关的文章和资料,这篇文章分享一下QAP问题的理解。
程序员,大多数时间在学习和训练逻辑推理的质量和速度,以逻辑清晰,明了为目标。随着年龄的增长,身体的各方面的机能的下降,逻辑推理和组织的能力也会下降。正是这种下降,给程序员带来了无限的焦虑,赖于“生存”的快速逻辑推理能力不再是优势。学会积累,学会“延迟满足”和”复利效应“,是治愈的良药。积累,也就是让自己理解的逻辑能在时间维度上,让更多人获得帮助。
前一段时间,介绍了零知识证明的入门知识,通过 QSP 问题证明来验证另外一个 NP 问题的解。最近在看 QAP 问题相关的文章和资料,这篇文章分享一下 QAP 问题的理解。
背景介绍
QSP/QAP 问题的思想都是出自 2012 年一篇论文:Quadratic Span Programs and Succinct NIZKs without PCPs

这篇论文提出了使用 QSP/QAP 问题,而不使用 PCP 方式,实现零知识证明。
术语介绍
- SP - Span Program ,采用多项式形式实现计算的验证。
- QSP - Quadratic Span Program,QSP 问题,实现基于布尔电路的 NP 问题的证明和验证。
- QAP - Quadratic Arithmetic Program,QAP 问题,实现基于算术电路的 NP 问题的证明和验证,相对于 QSP,QAP 有更好的普适性。
- PCP - Probabilistically Checkable Proof ,在 QSP 和 QAP 理论之前,学术界主要通过 PCP 理论实现计算验证。PCP 是一种基于交互的,随机抽查的计算验证系统。
- NIZK - Non-Interactive Zero-Knowledge,统称,无交互零知识验证系统。NIZK 需要满足三个条件:1/ 完备性(Completeness),对于正确的解,肯定存在相应证明。 2/可靠性 (Soundness) ,对于错误的解,能通过验证的概率极低。3/ 零知识。
- SNARG - Succinct Non-interactive ARGuments,简洁的无须交互的证明过程。
- SNARK - Succinct Non-interactive ARgumentss of Knowledge,相比 SNARG,SNARK 多了 Knowledge,也就是说,SNARK 不光能证明计算过程,还能确认证明者“拥有”计算需要的 Knowledge(只要证明者能给出证明就证明证明者拥有相应的解)。
- zkSNARK - zero-knowledge SNARK,在 SNARK 的基础上,证明和验证双方除了能验证计算外,验证者对其他信息一无所知。
- Statement - 对于 QSP/QAP,和电路结构本身(计算函数)相关的参数。比如说,某个计算电路的输入/输出以及电路内部门信息。Statement 对证明者和验证者都是公开的。
- Witness - Witness 只有证明者知道。可以理解成,某个计算电路的正确的解(输入)。
QAP 问题的定义
QAP 的定义和 QSP 的定义有些相似(毕竟都是一个思想理论的两种形式)。论文中给出了 QAP 的一般定义和强定义。QAP 的强定义如下:
QAP 问题是这样一个 NP 问题:给定一系列的多项式,以及给定一个目标多项式,找出多项式的组合能整除目标多项式。输入为 n 位的 QAP 问题定义如下:
- 给定多个多项式: $v_0, ... , v_m, w_0, ... , w_m, y_0, ... , y_m$
- 目标多项式: $t$
- 映射函数: $$ f: \left{(i, j) |1\leq i \leq n, j\in{0,1} \right} \to \left{1, ... m\right} $$
给定一个证据(Witness)u,满足如下条件,即可验证 u 是 QAP 问题的解:
- $$ a_k, b_k, c_k = 1\ \ 如果 k = f(i, u[i]) $$
- $$ a_k, b_k, c_k = 0\ \ 如果 k = f(i, 1- u[i]) $$
- $$ (v0(x) + \sum{k=1}^m a_k \cdot v_k(x)) \cdot (w0(x) + \sum{k=1}^m b_k \cdot w_k(x)) - (y0(x) + \sum{k=1}^m c_k \cdot y_k(x)) 能整除 t(x) $$
对一个证据 u,对每一位进行两次映射计算( $u[i]$ 以及 1-u[i] ),确定多项式之间的系数($ a_1,..,a_m,,和 b_1,.., b_m,以及 c_1, .., c_m$ 相等)。
算术电路
算术电路可以简单看成由如下的三种门组成:加门,系数乘法门以及通用乘法门(减法可以转化为加法,除法可以转化为乘法)。Vitalik 在 2016 年写过的QAP介绍,深入浅出的解释 NP 问题的算术电路生成和 QAP 问题的转化,推荐大家都读一读。
以 Vitalik 文章中的例子为例,算术逻辑( $x^3 + x + 5$ )对应的电路如下图所示:
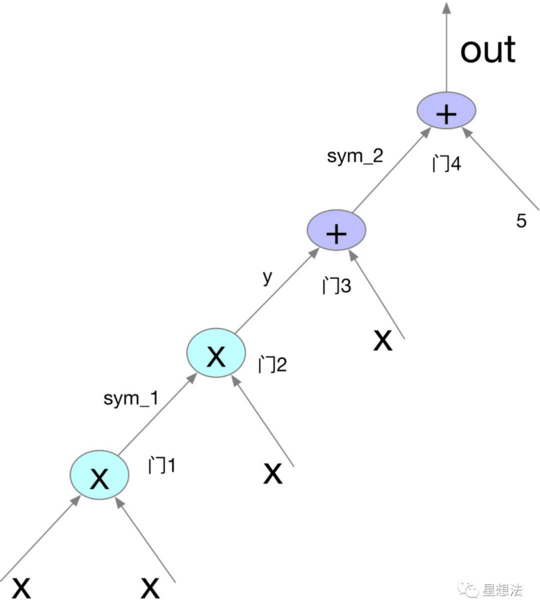
QAP 问题的转化
把一个算术电路转化为 QAP 问题的过程,其实就是将电路中的每个门描述限定的过程,也就是所谓的 R1CS (Rank-1 constraint system)。
算术电路拍平
算术电路拍平,就是用一组向量定义算术电路中的所有的变量(包括一个常量变量)。比如 2 中所示的电路,拍平之后的向量表示为 $[one, x, out, sym_1, y, sym_2 ]$ ,其中 one 代表常量变量,x 代表输入,out 代表输出,其他是中间门电路的输出。
假设一个合理的电路向量值为 $s - [s_0, s_1, s_2, s_3, s_4, s_5]$ 。
门描述
对于每个电路中的门进行描述,说清输入以及输出,采用
$$ s \cdot a* s \cdot b - s \cdot c = 0 $$
的形式,其中 $a,b,c$ 都是和电路向量长度一致的向量值。 $s \cdot a, s \cdot b, s \cdot c$ 都是点乘。这种形式表达的是“乘法门”。可以简单的理解, $a, b, c和s$ 的点乘就是“挑选”向量中的变量,查看挑选出的变量是否满足 $A * B = C$ 。
各个门对应的 $a, b, c$ 的向量值如下:
门 1 (查看 $x * x 是否等于 sym_1$ ):
$a = [0, 1, 0, 0, 0, 0]$
$b = [0, 1, 0, 0, 0, 0]$
$c = [0, 0, 0, 1, 0, 0]$
门 2 (查看 $sym_1 * x 是否等于 y$ ):
$a = [0, 0, 0, 1, 0, 0]$
$b = [0, 1, 0, 0, 0, 0]$
$c = [0, 0, 0, 0, 1, 0]$
门 3 (查看 $(x + y)*1 是否等于 sym_2$ ):
$a = [0, 1, 0, 0, 1, 0]$
$b = [1, 0, 0, 0, 0, 0]$
$c = [0, 0, 0, 0, 0, 1]$
门 4 (查看 $(5x + sym_2) * 1 是否等于out$ ):
$a = [5, 0, 0, 0, 0, 1]$
$b = [1, 0, 0, 0, 0, 0]$
$c = [0, 0, 1, 0, 0, 0]$
多项式表达
在门电路描述的基础上,将所有的门电路,转化为多项式表达。将 $a, b, c$ 中的每个系数,看成一个多项式的结果(以 a 为例): $a = [f_0(x), f_1(x), f_2(x), f_3(x), f_4(x), f_5(x)]$ 。
针对门 1/门 2/门 3/门 4, $f_0(x), f_1(x), f_2(x), f_3(x), f_4(x), f_5(x)$ 的取值不同。比如说:门 1 的 a 的 $f_0(x)$ 为 0,门 2 的 a 的 $f_0(x)$ 为 0,门 3 的 a 的 $f_0(x)$ 为 0,门 4 的 a 的 $f_0(x)$ 为 5。
设定门 1 对应的 x 为 1,门 2 对应的 x 为 2,门 3 对应的 x 为 3,门 4 对应的 x 为 4 的话(这些值可以任意指定),会得到如下的等式:
$f_0(1) = 0, f_0(2) = 0, f_0(3)=0, f_0(4)=5$
在获知一系列的输入和输出的前提下,可以通过拉格朗日定理,获取多项式表达式。小伙伴可以通过这个工具计算多项式。
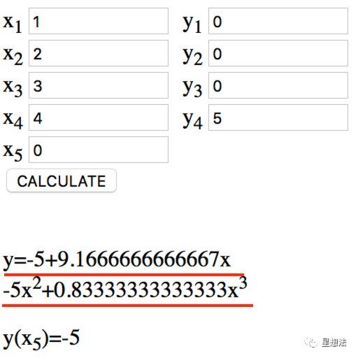
也就是说,a 的 $f_0(x) = -5 + 9.167x + -5x^2 + 0.833x^3$ 。同样的方式,可以算其他参数的 $f_0(x), f_1(x), f_2(x), f_3(x), f_4(x), f_5(x)$ 。再把这些多项式代入
$$ s \cdot a* s \cdot b - s \cdot c = 0 $$
,在正确的 $s$ 向量值的情况下,1/2/3/4 能让等式成立,也就是说,多项式 $s \cdot a* s \cdot b - s \cdot c$ 能整除 $(x-1)(x-2)(x-3)(x-4)$ 。这样,一个算术电路就转化为了 QAP 问题。
QAP 问题的 zkSNARK 证明
QAP 问题的 zkSNARK 证明过程和 QSP 有点类似。skSNARK 证明过程分为两部分:a) setup 阶段 b)证明阶段。QAP 问题就是给定一系列的多项式 $v_0, ..., v_m, w_0, ..., w_m, y_0, ... , y_m$ 以及目标多项式 $t$ ,证明存在一个证据 $u$ 。这些多项式中的最高阶为 $d$ 。
setup 和 CRS
CRS - Common Reference String,也就是预先 setup 的公开信息。在选定 $s$ 和 $\alpha$ 的情况下,发布如下信息:
-
$s$ 和 $\alpha$ 的计算结果
$(s^0), E(s^1), ... , E(s^d)$
$E(\alpha s^0), E(\alpha s^1), ... , E(\alpha s^d)$
-
多项式的 $\alpha$ 对的计算结果 $E(t(s)), E(\alpha t(s))$
$E(v_0(s)), ... E(v_m(s)), E(\alpha v_0(s)), ..., E(\alpha v_m(s))$
$E(w_0(s)), ... E(w_m(s)), E(\alpha w_0(s)), ..., E(\alpha w_m(s))$
$E(y_0(s)), ... E(y_m(s)), E(\alpha y_0(s)), ..., E(\alpha y_m(s))$
-
多项式的 $\beta_v, \beta_w, \beta_y, \gamma$ 参数的计算结果 $E(\gamma), E(\beta_v\gamma), E(\beta_w\gamma), E(\beta_y\gamma)$
$E(\beta_vv_1(s)), ... , E(\beta_vv_m(s))$
$E(\beta_ww_1(s)), ... , E(\beta_ww_m(s))$
$E(\beta_yy_1(s)), ... , E(\beta_yy_m(s))$
$E(\beta_vt(s)), E(\beta_wt(s)), E(\beta_yt(s))$
证明者提供证据
在 QAP 的映射函数中,如果 2n < m ,1, ..., m中有些数字没有映射到。这些没有映射到的数字组成 $I_{free}$ ,并定义( $k$ 为未映射到的数字):
$v_{free}(x) = \sum_k a_kv_k(x)$
证明者需提供的证据如下:
- $V{free} := E(v{free}(s)), \ W := E(w(s)), \ Y := E(y(s)), \ H := E(h(s)),$
- $V{free}' := E(\alpha v{free}(s)), W' := E(\alpha w(s)), Y' := E(\alpha y(s)), H' := E(\alpha h(s)), $
- $P := E(\betavv{free}(s) + \beta_ww(s) + \beta_yy(s))$
$V{free}/V{free}', W/W', Y/Y', H/H' 是 \alpha 对,用以验证v{free},w,y,h 是否是多项式形式。 $ $ t 是已知,公开的,毋需验证, P 用来确保 v{free}(s), w(s) 和 y(s)的计算采用一致的参数。$
验证者验证
在QAP的映射函数中,如果2n < m,1, ..., m中所有映射到的数字作为组成系数组成的二项式定义为(和$v_{free}$互补):
$v_{in}(x) = \sum_k a_kv_k(x)$
验证者需要验证如下的等式是否成立:
- $e(V{free}', g) = e(V{free}, g^\alpha), e(W', E(1)) = e(W, E(\alpha)), e(Y', E(1)) = e(Y, E(\alpha)), e(H', E(1)) = e(H, E(\alpha))$
- $e(E(\gamma), P) = e(E(\betav\gamma), V{free})e(E(\beta_w\gamma), W)e(E(\beta_y\gamma), Y)$
- $e(E(v0(s))E(v{in}(s))V_{free}, E(w_0(s))W) = e(H, E(t(s)))e(y_0(s)Y, E(1))$
第一个(系列)等式验证$V{free}/V'{free}, W/W', Y/Y', H/H'是否是\alpha对$。
第二个等式验证$V{free}, W, Y$的计算采用一致的参数。因为$v{free}, w, y$都是二项式,它们的和也同样是一个多项式,所以采用$\gamma$ 参数进行确认。证明过程如下:
$e(E(\gamma), P) = e(E(\gamma), E(\betavv{free}(s) + \beta_ww(s) + \beta_yy(s))) = e(g, g)^{\gamma(\betavv{free}(s) + \beta_ww(s) + \beta_yy(s))}$
$e(E(\betav\gamma), V{free})e(E(\beta_w\gamma), W)e(E(\beta_y\gamma), Y) = e(E(\betav\gamma), E(v{free}(s)))e(E(\beta_w\gamma), E(w(s)))e(E(\beta_y\gamma), E(y(s)))$
$= e(g,g)^{(\betav\gamma)v{free}(s)}e(g,g)^{(\beta_w\gamma)w(s)}e(g,g)^{(\beta_y\gamma)y(s)}= e(g, g)^{\gamma(\betavv{free}(s) + \beta_ww(s) + \beta_yy(s))}$
第三个等式验证$v(s)w(s) - y(s) = h(s)t(s)$,其中$v0(s)+v{in}(s)+v_{free}(s) = v(s)$。
简单的说,逻辑是确认$v, w, y, h$是多项式,并且$v,w,y$采用同样的参数,满足$v(s)w(s)- y(s)= h(s)t(s)$。
到目前为止,整个QAP的zkSNARK的证明过程逻辑已见雏形。
$\delta $ 偏移
为了进一步“隐藏” $V{free}, W, Y$,额外需要采用两个偏移: $\delta{free}, \delta_w 和 \deltay$。 $v{free}(s)/w(s)/y(s)/h(s)$进行如下的变形,验证者用同样的逻辑验证。
$v{free}(s) \rightarrow v{free}(s) + \delta_{free}t(s)$ $w(s) \rightarrow w(s) + \delta_wt(s)$ $y(s) \rightarrow y(s) + \deltayt(s)$ $h(s) \rightarrow h(s)+\delta{free}(w_0(s) + w(s)) + \delta_w(v0(s) + v{in}(s) + v{free}(s)) + (\delta{free}\delta_w)t(s) - \delta_y$
总结:
QAP和QSP问题类似。QSP问题主要用于布尔电路计算表达,QAP问题主要用于算术电路计算表达。将一个算术电路计算转化为QAP问题的过程,其实就是对电路中每个门电路进行描述限制的过程。通过朗格朗日定理,实现算术电路的多项式表达。QAP问题的zkSNARK的证明验证过程和QSP非常相似。
本文作者 Star Li,他的公众号星想法有很多原创高质量文章,欢迎大家扫码关注。

- ZK编年史:哈希登场 118 浏览
- 以太坊协议研究学习小组 - 2026 启动 224 浏览
- 神奇的 Zig、C 和 OpenSSL 184 浏览
- Layer Zero 发布 Zero 链:去中心化的多核世界计算机 331 浏览
- “Jolt Inside” - 构建者需要了解的全新武器 277 浏览
- 以太坊的下一个重大转变:从重新执行每笔交易到验证 ZK 证明 354 浏览
- Shamir份额的魔力:BLS门限签名 448 浏览
- Zcash:比特币遗忘的隐私 425 浏览
- ZK编年史:计算模型 291 浏览
- lambdaworks 2026 年更新路线图和优先级 348 浏览
- 2026年构建机构级DeFi平台真正需要什么 876 浏览
- zkMesh:2026年1月回顾 442 浏览

