零知识证明 - Groth16计算详解

Groth16算法是zkSNARK的典型算法，目前在ZCash，Filecoin，Coda等项目中使用。本文从计算量的角度详细分析Groth16计算。Groth16计算分成三个部分：Setup针对电路生成Pk/Vk（证明/验证密钥），Prove在给定witness/statement的情况下生成证明，Verify通过Vk验证证明是否正确。

本文中所有的术语和数学符号和Groth16论文保持一致（On the Size of Pairing-based Non-interactive Arguments，具体的计算在17/18页）：

对Groth16算法的理解可查看：

零知识证明 - Groth16算法介绍

对libSnark代码库的理解可查看：

零知识证明 - libsnark源代码分析

1. 电路描述

所有的电路描述有个专业的术语：Relation（变量和变量的关系描述）。描述Relation的语言很多：R1CS，QAP，tinyRAM，bacs等等。目前开发，电路一般采用R1CS语言描述。R1CS相对来说，非常直观。A*B=C（A/B/C分别是输入变量的线性组合）。但是，要应用Groth16算法，需要将R1CS描述的电路，转化为QAP描述。两种电路描述语言的转化，称为Reduction。

1.1 R1CS描述

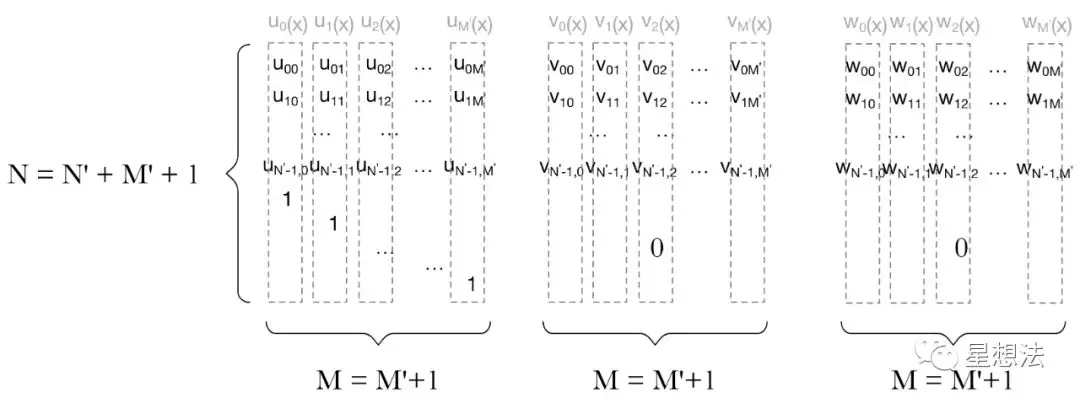
给定M'个变量（第一个变量约定为恒量1），以及N'个约束，所有的R1CS描述可以表示如下：

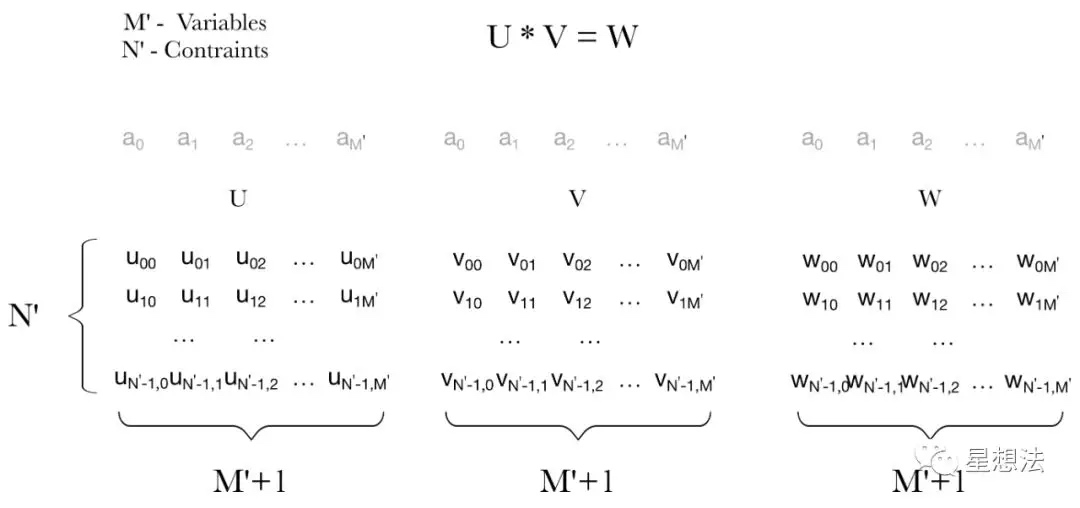
每一行是一个约束。举例，第一行的约束表示的是：

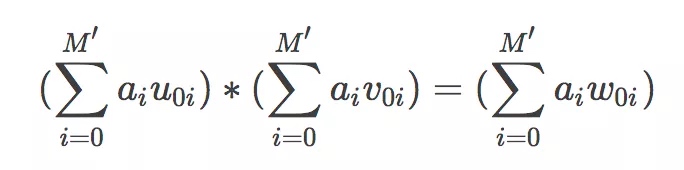
1.2 QAP转化

介绍具体的转化之前，先介绍一个简单的术语，拉格朗日插值以及拉格朗日basis。

给定一系列的x和y的对应关系，通过拉格朗日插值的方式，可以确定多项式：

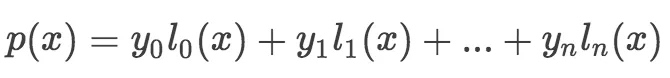
其中$ l_0(x),l_1(x),...l_n(x) $就称为拉格朗日basis，计算公式如下：

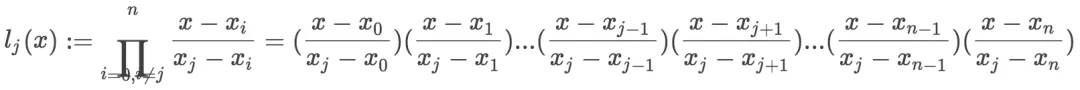
简单的说，在给定一系列的x/y的对应关系后，可以通过拉格朗日插值表示成多项式。在R1CS的表达方式下，U/V/W多项式很自然用拉格朗日basis表示，并不是以多项式的系数表示。 在R1CS转化为QAP之前，必须对现有约束进行增强，增加$ a_i*0=0 $的约束。增加这些约束的原因是为了保证转化后的QAP的各个多项式不线性依赖。

1.3 domain选择

针对每个变量，已经知道N个y值。如何选择这些y值，对应的x值？这个就是domain的选择。选择domain，主要考虑两个计算性能：

1. 拉格朗日插值
2. FFT和iFFT。

libfqfft的源码提供了几种domain：

1. Basic Radix-2
2. Extended Radix-2
3. Step Radix-2
4. Arithmetic Sequence
5. Geometric Sequence

选择哪一种domain和输入个数（M）有关。为了配合特定domain的计算，domain的阶（M）会稍稍变大。

确定了domain，也就确定了domain上的一组元素s：

2. Setup计算

随机生成 $ \alpha,\beta,\gamma,\delta,x \in F_r $ 。注意这里的和上一节中的x含义不同，不要混淆。

2.1 拉格朗日插值

已知的情况下，通过1.2的公式，先通过domain计算拉格朗日basis。再乘上系数，可以获得$ u_i(x),v_i(x),w_i(x) $。这些多项式的阶是M。

2.2 计算$x^i$ 和 $t(x)$

$ x^i $ 的计算相对简单，注意幂次计算都是在$ F_r $的计算。在domain确定后，多项式t也确定，从而可以计算出$ t(x) $。

2.3 生成Pk/Vk

按照如下的公式，计算Pk/Vk。$ \sigma_1 $ 是G1上的点，$ \sigma_2 $是G2上的点。

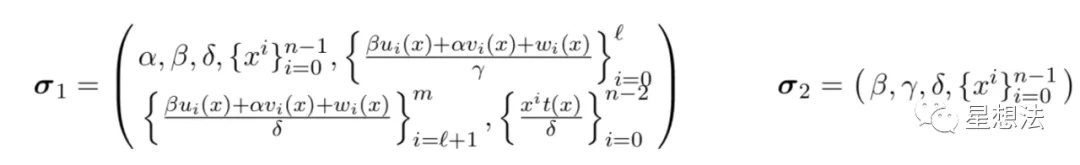
其中，

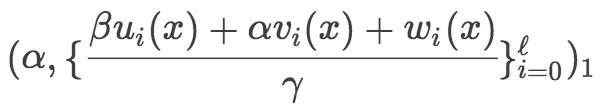
是Vk。其他部分是Pk。可以看出，Vk的大小取决于公共输入的变量个数，相对来说数量比较小。Pk的数据量大小和所有的变量个数相关。计算过程，主要由scalarMul组成。

3. Prove计算

在domain选择后，U*V=W，可以变换为如下的多项式方程：

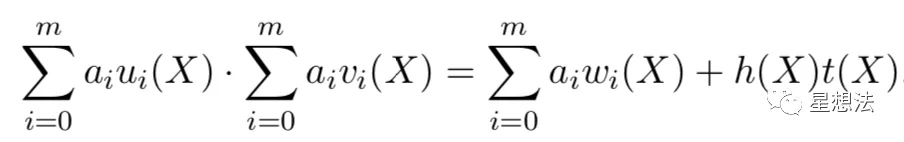
3.1 多项式系数$ u_i(x),v_i(x),w_i(x) $多项式系数

通过iFFT，在已知domain上元素s和值对应关系，可以计算出多项式系数。

3.2 $u_i(x),v_i(x),w_i(x)$ 在coset的值

$ u_i(x),v_i(x),w_i(x) $在coset的值 已知多项式系数，通过FFT，计算出多项式在coset的值。注意，元素s以及对应的coset是特殊设计的，便于FFT/iFFT的计算，和domain的选择有关系。

3.3 h(X)在coset的值

h(X)多项式的计算公式如下：

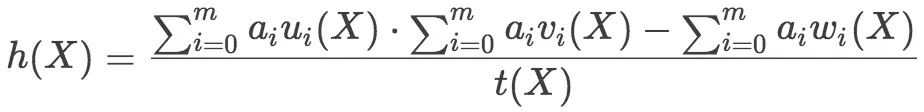
代入3.1/3.2，直接计算出h(X)在coset的值。

3.4 计算h(X)多项式系数

通过iFFT，获取h(X)的多项式系数，阶为N-2。

3.5 生成证明

随机选择$ r,s \in F_r $，在已知$ u_i(x),v_i(x),w_i(x),h(x) $的情况下，通过如下的公式计算证明A，B，C：

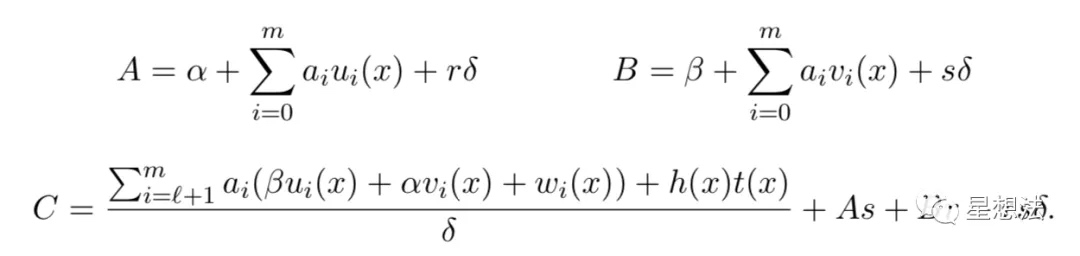
其中，A需要计算在G1上的点，B需要计算在G1/G2上的点，C需要计算G1上的点。C中$ \frac{h(x)t(x)}{\delta} $计算如下：

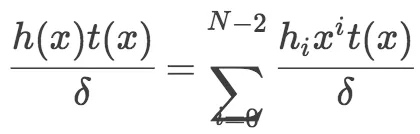
很显然，生成证明的计算量主要由四个Multiexp组成（A-1，B-1，C-2），和变量个数以及约束的个数有关。在一个大型电路中，生成证明的时间比较长（秒级，甚至分钟级）。

4. Verify计算

在已知证明以及Vk的情况下，通过配对（pairing）函数，很容易计算如下的等式是否成立。计算在毫秒级。

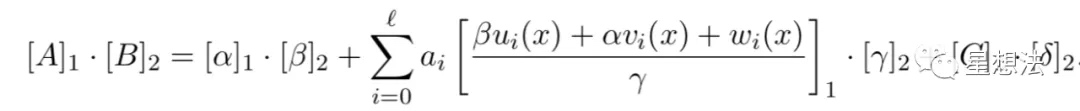
总结：

Groth16算法的主要计算量由两部分组成：FFT/iFFT以及MultiExp。在生成证明时，需要4次iFFT以及三次FFT计算。Setup计算和生成证明时，需要大量的MultiExp。Verify计算量相对较小。

我是Star Li，我的公众号星想法有很多原创高质量文章，欢迎大家扫码关注。