哈希的奇妙之处：SHA-256、Pedersen 和 Poseidon

哈希的奇妙之处：SHA-256、Pedersen 和 Poseidon

以太坊正在快速发展，我们现在可以创建零知识证明 (ZKP) 来证明交易，而无需泄露私人信息。这些通常是 SNARK、STARK 和 Bulletproof，这些方法可以有效地将交易添加到区块链上，并且不需要大量的检查。但是，我们现有的哈希方法并非设计为在区块链基础设施中良好运行，因此我们必须找到替代方案。

使用零知识证明电路，我们通常必须证明某个加密哈希函数原像的知识。对于：

H( a)= b

a 是 b 的原像。此原像可能是密钥、密码或某人的私人信息。因此，我们可以通过哈希其数字形式来证明几乎任何事情。

因此，此证明的核心是哈希方法的使用及其与区块链的集成。为此，我们现有的哈希方法在计算时间和创建 ZKP 电路方面可能成本高昂。这可能会增加 gas 成本。总的来说，我们需要将哈希方法约束为有限域运算，因为这些运算符合我们的区块链智能合约方法，并允许我们有效地构建 ZKP 电路。这些方法是 Pedersen 哈希 （它使用椭圆曲线数学）和 Poseidon 哈希 （它使用有限域计算）。

哈希方法

我很幸运能与 Merkle-Damgård (MD2/MD4/MD5) 哈希方法的两位共同发明人 Ralph Merkle 和 Ivan Damgård 交谈。因此，哈希方法的发展一直是网络安全的真正奇迹，其中任何具有 SHA-256 安全级别的都可以被视为安全的。如果我们看一下区块链，ECDSA 签名存在一个威胁，但每个区块的安全性都通过 SHA-256 和 Merkle 树来保护。因此，所有已创建的区块（以及未来的区块）都是安全的，即使交易签名存在被破解的风险。

我们现在使用的三种核心哈希方法是 SHA-256、SHA-3（又名 Keccak）和 Blake2。最流行的是 SHA-256，它使用 MD 类型的结构：

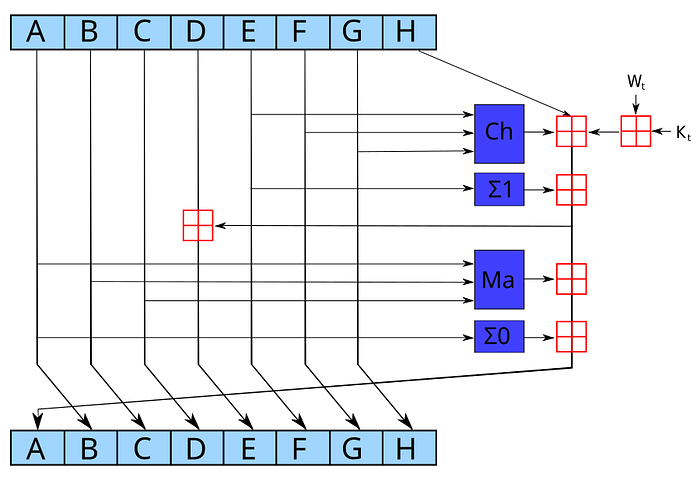
参考 [ 这里]

参考 [ 这里]

我们可以看到，存在大量的位移 (>>>)，并使用了 NOT（带有向下线的线）、XOR（带有圆圈的“+”）和 AND（向上的箭头）。红色部分对 SHA-256 进行以 2³² 为模的加法。

Pedersen 哈希

Pedersen 哈希涉及将消息拆分为 k 个块（ m 1, m 2 … mk），然后使用这些块基于多个生成器点（ G 1, G 2 … Gk）生成一系列椭圆曲线点。然后，哈希是所创建点的加法： H = m 1. G 1+ m 2. G 2+ m 3. G 3。

如果我们使用三个块，则将消息分为三个：

m = m 1|| m 2|| m 3

然后，我们生成三个间隔良好的生成器点：

G 1, G 2, G 3

在你的收件箱中获取 Prof Bill Buchanan OBE FRSE 的文章

免费加入 Medium 即可获得这位作家的更新。

Pedersen 哈希然后是：

Hash =( m 1). G 1+( m 2). G 2+( m 3). G 3

其中 ( m 1). G 1, ( m 2). G 2 和 ( m 3). G 3 是曲线上的点。

让我们采用 Tiny Jubjub 曲线上的三个点 [ 这里]：

gx1,_ := new(big.Int).SetString("18930368022820495955728484915491405972470733850014661777449844430438130630919",10 )
    gy1,_ := new(big.Int).SetString("0",10)

gx2,_ := new(big.Int).SetString("12576558175125128246374296641007938322302911659474853157208587689687229831284",10 )
 gy2,_ := new(big.Int).SetString("3",10)

 gx3,_ := new(big.Int).SetString("18869612826929474874643025262839512853875949931275176402223244870011103237908",10 )
 gy3,_ := new(big.Int).SetString("5",10)

然后我们可以使用以下代码计算哈希值 [ 这里]：

package main

import (
 "fmt"
 "github.com/iden3/go-iden3-crypto/v2/babyjub"
 "math/big"
 "encoding/hex"
 "os"
)
func splitMessage(inStr string, size int) []string { // splitMessage 函数，将输入字符串 inStr 分割成指定大小 size 的切片
   var elements []string
   elementSize := len(inStr) / size  // 计算每个元素的大小
   for i := 0; i < size; i++ {
      start := i * elementSize   // 计算起始位置
      end := start + elementSize    // 计算结束位置
      if i == size-1 {          // 如果是最后一个元素, 则结束位置为字符串末尾
         end = len(inStr)
      }
      elements = append(elements, inStr[start:end]) // 将分割后的字符串添加到 elements 切片中
   }
   return elements // 返回分割后的字符串切片
}
func main() { // main 函数
// Baby Jubjub 曲线上的三个生成器值：
//19763400273586758549882294695966112539108188722254631372974345487113325868230, 13
//12576558175125128246374296641007938322302911659474853157208587689687229831284, 3
//18869612826929474874643025262839512853875949931275176402223244870011103237908, 5

 str:="Testing 123" // 设置默认字符串 "Testing 123"
 argCount := len(os.Args[1:]) // 获取命令行参数的数量
 if (argCount>0) {str= string(os.Args[1])} // 如果有命令行参数, 则使用第一个参数作为字符串
 fmt.Printf("Input message: %s\n\n",str) // 打印输入的消息

 value := hex.EncodeToString([]byte(str)) // 将字符串转换为十六进制编码的字符串
 res:= splitMessage(value,3)  // 将十六进制编码的字符串分割成三个部分
 gx1,_ := new(big.Int).SetString("19763400273586758549882294695966112539108188722254631372974345487113325868230",10 ) // 初始化大整数 gx1
 gy1,_ := new(big.Int).SetString("13",10)   // 初始化大整数 gy1
 gx2,_ := new(big.Int).SetString("12576558175125128246374296641007938322302911659474853157208587689687229831284",10 ) // 初始化大整数 gx2
 gy2,_ := new(big.Int).SetString("3",10)   // 初始化大整数 gy2

 gx3,_ := new(big.Int).SetString("18869612826929474874643025262839512853875949931275176402223244870011103237908",10 ) // 初始化大整数 gx3
 gy3,_ := new(big.Int).SetString("5",10)   // 初始化大整数 gy3

 G1 := &babyjub.Point{X: gx1, Y: gy1}  // 创建 Baby Jubjub 曲线上的点 G1
 G2 := &babyjub.Point{X: gx2, Y: gy2}  // 创建 Baby Jubjub 曲线上的点 G2
 G3 := &babyjub.Point{X: gx3, Y: gy3}  // 创建 Baby Jubjub 曲线上的点 G3

 fmt.Printf("G1 (%s, %s)\n",G1.X.String(),G1.Y.String()) // 打印 G1 的坐标
 fmt.Printf("G2 (%s, %s)\n",G2.X.String(),G2.Y.String()) // 打印 G2 的坐标
 fmt.Printf("G3 (%s, %s)\n\n",G3.X.String(),G3.Y.String()) // 打印 G3 的坐标

 m_1,_:=hex.DecodeString(res[0])  // 将分割后的第一个字符串从十六进制解码为字节数组
 m_2,_:=hex.DecodeString(res[1])  // 将分割后的第二个字符串从十六进制解码为字节数组
 m_3,_:=hex.DecodeString(res[2])  // 将分割后的第三个字符串从十六进制解码为字节数组
 M1:=new(big.Int).SetBytes(m_1)   // 将字节数组转换为大整数 M1
 M2:=new(big.Int).SetBytes(m_2)   // 将字节数组转换为大整数 M2
 M3:=new(big.Int).SetBytes(m_3)   // 将字节数组转换为大整数 M3

  M1_G1 := babyjub.NewPoint().Mul(M1,G1)  // 计算 M1 * G1
  M2_G2 := babyjub.NewPoint().Mul(M2,G2)  // 计算 M2 * G2
  M3_G3 := babyjub.NewPoint().Mul(M3,G3)  // 计算 M3 * G3
 M1_G1_M2_G2 := babyjub.NewPoint().Projective().Add(M1_G1.Projective(),M2_G2.Projective()) // 计算 M1 * G1 + M2 * G2

 M1_G1_M2_G2_M3_G3 := babyjub.NewPoint().Projective().Add(M1_G1_M2_G2,M3_G3.Projective()) // 计算 M1 * G1 + M2 * G2 + M3 * G3

 fmt.Printf("(%d).G1 Point (%s, %s)\n",M1,M1_G1.X.String(),M1_G1.Y.String()) // 打印 M1 * G1 的坐标
 fmt.Printf("(%d).G2 Point (%s, %s)\n",M2,M2_G2.X.String(),M2_G2.Y.String()) // 打印 M2 * G2 的坐标
 fmt.Printf("(%d).G3 Point (%s, %s)\n\n",M3,M3_G3.X.String(),M3_G3.Y.String()) // 打印 M3 * G3 的坐标
 fmt.Printf("Result: (%s, %s)\n\n",M1_G1_M2_G2_M3_G3.X.String(),M1_G1_M2_G2_M3_G3.Y.String()) // 打印最终结果的坐标

 fmt.Printf("Pedersen Hash: %s\n",M1_G1_M2_G2_M3_G3.X.String()) // 打印 Pedersen 哈希值
}

结果是 [ 这里]：

Input message (in hex): 010203040506070809

G1 (19763400273586758549882294695966112539108188722254631372974345487113325868230, 13)
G2 (12576558175125128246374296641007938322302911659474853157208587689687229831284, 3)
G3 (18869612826929474874643025262839512853875949931275176402223244870011103237908, 5)

(66051).G1 Point (16037773783835146438558403421260836675868272902364849599426875451057520106906, 14728403640743494614641112385959960394789183729111213630842711014573474773378)
(263430).G2 Point (11852499477985754981114582499827808786287610741986412935345795152171632055691, 2674722056485308817737914684425248014914348605929003485370677590616611371783)
(460809).G3 Point (7621534404334108830225350985637201742729050263412910533478640032004698408257, 3768640800306573992890050298007966758509235918251221830887953108815318470075)

Result: (8246050116631628695869530651297899884448852706174930565536327904583775502268, 21660911736906458468630355032769751803544552633662219825808465470014769680600)
Pedersen Hash: 8246050116631628695869530651297899884448852706174930565536327904583775502268

当然，在现实生活中，我们会将生成器点分隔开。

Poseidon 哈希

Poseidon [1] 和 Poseidon 2 [2] 哈希函数专注于可验证的计算协议，并在素数域上产生小的电路尺寸。它们通常用于零知识证明应用程序中，例如以太坊，并且在 STARK 基准测试中具有出色的性能。总的来说，Poseidon 哈希使用 sponge 函数（与 SHA-3 (Keccak) 一起使用）进行哈希，因此包含一个状态。字段本身约为 255 位，并提供约 116 位的安全性。

在本例中，我们将采用一个三值向量并计算 Poseidon 哈希 [ 这里]：

package main

import (
    "fmt"
    "github.com/iden3/go-iden3-crypto/v2/babyjub"
    "math/big"
    "strconv"
    "os"

)

func main() { // main 函数

    start:=0 // 定义起始值为 0
    points:=10 // 定义点的数量为 10

    valid_points:=0 // 定义有效点的数量为 0

    argCount := len(os.Args[1:]) // 获取命令行参数的数量

    if argCount > 0 { // 如果存在命令行参数
        start,_ = strconv.Atoi(os.Args[1]) // 将第一个参数转换为整数，并赋值给 start
    }

    if argCount > 1 { // 如果存在第二个命令行参数
        points,_ = strconv.Atoi(os.Args[2]) // 将第二个参数转换为整数，并赋值给 points
    }

    if (points>50) { // 如果点的数量大于 50
        fmt.Printf("Too many points") // 打印 “Too many points”
        return // 退出程序
    }

    end:=start+points // 计算结束值

    y:=big.NewInt(int64(start)) // 创建一个新的大整数，初始值为 start

    for i:=start;i<end;i++ { // 循环遍历从 start 到 end 的值

        P,err:= babyjub.PointFromSignAndY(true,y) // 从签名和 Y 坐标创建一个 babyjub 点

        if (err==nil) { // 如果没有错误发生

            fmt.Printf("P Point (%s, %s)\n",P.X.String(),P.Y.String()) // 打印点的 X 和 Y 坐标
            valid_points=valid_points+1 // 有效点数量加 1
        } else { // 如果发生错误
            fmt.Printf(" No point at y=%d. Error: %v\n", y,err) // 打印错误信息
        }
        y = y.Add(y,big.NewInt(1)) // y 的值加 1

    }
    fmt.Printf("\nNumber of valid points: %d\n", valid_points) // 打印有效点的数量

}

[1]、[1, 4] 和 [1, 4, 3] 向量的示例如下 [ 这里]：

Inputs 1. Poseidon Hash: 18586133768512220936620570745912940619677854269274689475585506675881198879027

Inputs 1, 4. Poseidon Hash: 20093115681644140910448217843618788628911204837480265095337820971629649645527

Inputs 1, 4, 3. Poseidon Hash: 11581812134676561997526789540623636669301006969489560800875483048762369668960

结论

参考文献

[1] Grassi, L., Khovratovich, D., Rechberger, C., Roy, A., & Schofnegger, M. (2021). Poseidon: A new hash function for {Zero-Knowledge} proof systems. In 30th USENIX Security Symposium (USENIX Security 21) (pp. 519–535).

[2] Grassi, L., Khovratovich, D., & Schofnegger, M. (2023, July). Poseidon2: A faster version of the poseidon hash function. In International Conference on Cryptology in Africa (pp. 177–203). Cham: Springer Nature Switzerland.

• 原文链接： billatnapier.medium.com/...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～