密码学基础：零知识证明（第三部分）

这是关于加密技术的一系列更大文章的一部分。如果这是你第一次接触这篇文章，我强烈建议你从系列的开始开始。

在理论解释之后，是时候进入更实用的内容了！

在今天的文章中，我想专注于一些简单的例子，说明我们如何使用 zkSNARK，例如 Plonk，来证明一些声明。因此，我们基本上是在 构建一些算术电路。

我认为没有比重新审视 区间证明 更好的开始了！让我们直接进入主题。

重新审视区间证明（ Range Proofs）

在我们不算简短地看过 Bulletproofs 之后，我们看到从零开始构建一个区间证明是多么困难。但现在，我们手头有了一些新玩意儿。正如我们所承诺的，我们将看一下如何构建一个算术电路以表示这个声明：

存在一个有效的 N 位表示形式来表示一个数 v

构建这样一个电路可以让我们使用 Plonk 证明所述数字 v 的知识！那么让我们再次试着把这放入方程中。

事实上，这就是我们之前描述的同一个系统 我们之前说过。因此，接下来的描述将有些简化——我建议参考之前的解释以获得更多细节！

如果我们的数字 v 可以用 N 位表示，这意味着它有一些有效的二进制表示：

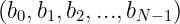
反过来，这些数字应该满足这个方程：

我们还知道我们的所有输入都将在一个大小为 q 的 有限域 中：

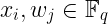
无论是 v 还是 bᵢ 都将是我们电路的输入——因此，我们需要某种方式来证明 bᵢ 值是 比特（要么 0 要么 1）。我们可以通过以下检查来做到这一点：

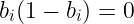
对于每一个 N 位。

减法

太好了！我们有了系统……但我们如何将其转化为算术电路？特别是，我们需要能够表示 减法，但我们只能使用 加法 和 乘法 门。该怎么办呢？

嗯……

好吧，在处理 有限域 时，有一个 加法逆元 的概念！想象一下 减去 1，相当于 加上 -1。但是，当然， -1 不是我们域中的元素：

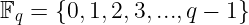
那么这如何帮助我们呢？你看，就像我们说当结果大于 q - 1 时，加法会 循环到 集的 开头，同样，当结果小于 0 时，减法也会 循环到 集的 末尾。

实际上，发生的事情是，我们可以通过使用 取模操作 将 -1 映射到该集合中：

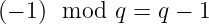
你可能会看到这被表示为 -1 ≡ q - 1 (mod q)。这称为同余关系，它表示“-1 在模 q 的情况下与 q - 1 相等”。

关于 同余关系 还有很多要说的，它们还定义了同余类——但我们今天将避免讨论这些主题。如果你感兴趣，可以在 这里 阅读。

总而言之，加上 q - 1 的效果与 减去 1 完全相同！

这对于加法 群 而言也是有效的。

把它放在一起

现在我们知道如何进行减法，我们可以构建我们电路！

首先，我们必须检查 bᵢ 是一个比特。这可以通过以下方式完成：

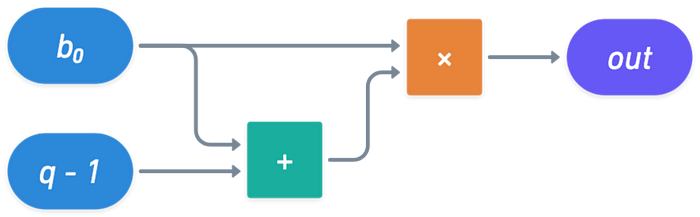
这表示 bᵢ(bᵢ — 1)。如果 bᵢ 是一个比特（要么 0 或者 1），输出应该为 0。

当然，如果我们将所有这些检查的输出相加，结果值也应该为 0。

然后，我们需要表示每个比特乘以相应的 2 的幂的总和。一旦我们获得结果，减去 v 也应该得到 0。正如你可能猜到的，减去 v 和加上 -v 是相同的，这当然是乘以 -1 和 v 的结果。

为了使事情变得可管理，假设 N = 4。对于这个数量的比特，我们的电路看起来像这样：

抱歉看起来有些凌乱，画电路不是我的强项。

就这样！当输入的数字 v 和它的二进制表示 b₀, b₁, b₂ 和 b₃ 被喂入时，此电路应输出 0。当然，我们不想揭示这两个——所以它们将作为 私密声明。所有其他输入可以视为 见证 的一部分——只是一些值，用于有效评估电路。

如果我们反顾之前文章中的术语，则 机密信息 和 见证 将是：

从这里开始，我们只需按照前一篇文章中介绍的方式应用 Plonk，然后我们就有一个 zkSNARK 来证明 v 在 0 到 15 的范围内。太好了！

集合成员资格

之前的例子引入了一些有趣的想法，比如 如何使用门进行减法。隐含之中，我们还使用了一些 魔法数字 作为输入，以避免过多的计算。

然而，这不是构建电路时我们可以使用的唯一技巧——正如我们将很快看到的那样。让我们继续下一个例子，看看我们面临的挑战。

想象一下我们有一组值 S：

我们将尝试证明某个值 sᵢ 的知识，该值 属于该集合。我们需要一些数学陈述来表示这一事实。这对于我们来说相当简单——我将在此为你写下方程：

这样就行了！

如果 sᵢ 确实是集合的一部分，那么其中一个项将为 零，导致整个乘积 为 0。否则， P(x) 的值将是某个正的非零值。

也就是说，sᵢ 是 P(x) 的根。

为这个多项式构建一个电路并不困难。它可能涉及提供值 sᵢ 作为见证，以加快计算，并让协议有意义。比如，证明在某个集合中的值的知识有什么用，如果验证者不知道他们所讨论的集合？

然而，这里似乎存在一个问题：如果 S 是公开的，那么 每个人 都可以读取它。因此，在理论上，任何人都可以证明对集合中某些 sᵢ 的知识。在这种情况下构建 零知识 证明并没有多大意义……

隐藏集合

解决这个问题并不难：为了使集合 保密，我们可以对每个元素 哈希，并公开哈希值。集合现在看起来是这样的：

现在我们说到点子上了。

进行这种调整后，知道集合 S’ 不会揭示 有关 S 中实际值的任何信息，这些值仍然是秘密的。我们的方程也需要稍微修改：

当然，哈希函数 H 必须哈希到我们的有限域，以便我们可以在电路中使用这些值。

太好了。绝妙。直到……我们注意到需要在我们的电路中 包含哈希函数。

呃-oh……

好吧，深呼吸。没那么糟糕。当然，如果我们不得不自己为哈希函数实现电路，那将是非常棘手的。

幸运的是，有人已经考虑到了这一点，并在一些流行的 领域专用语言（DSL）中提供哈希函数作为包，以构建电路，比如 Circom。

例如，有 Poseidon。你可以在 这里 找到实现。

让我们将哈希函数视为一个 盒子，我们会将其包含在我们的电路中，就像一个 组件。考虑到这一点，我们的电路将看起来像这样：

只要 x 在秘密集合中，该电路就应该输出 0。

太好了！剩下的就是通过 Plonk 运行它——你知道的，计算轨迹，编码，所有我们在该系列前一章 中已经讨论的好东西。

零检查

在我们的电路中包含一个可重用的哈希组件肯定是个好主意。人们可能会想，如果有其他 操作 或者 检查 也想通过类似的方式重用的话——因此，这类 黑盒 过程是一个很好的目标。

非常类似于创建计算机组件的过程！

很简单的想法是，构建一个检查某个值 是否为零 的组件。即，一个执行以下操作的函数：

我是说，这可能是有用的……谁知道呢，对吧？检查某些计算是否在一个大电路中 yield 0 可能是必要的！

让我们构建这样的组件。以下是它的构建思路：

更仔细的逐步检查揭示了这个电路所做的事情：前 三个门 计算如下表达式：

如果 x 是 0，那么它的 逆 也将为零，表达式将 yield 1。如果 x 不是 0，那么根据定义我们知道 x.x⁻¹ = 1，因此该表达式将返回 0。

这就是为什么此组件的 输出 不在最后一个门上，而在第三个门上的原因。那么为什么会有一个 第四个门？它的目的是什么？

为了回答这个问题，我问你：你没有在这个电路中注意到什么不寻常的事情吗？再次看看它。

你很快会发现，这是我们第一次使用 模逆。它是我们电路的一个 输入——我们只是 无法通过 加法和乘法门单独计算模逆。因此，模逆的值 必须 提供。

记住，在 Plonk 中，我们只是检查计算轨迹是否合理——只要我们确保该值是正确的，作为输入提供逆是完全可以的！

这个想法是第四个门作为检查所 声称的 模逆 是否实际上是 正确的。让我们称声称的模逆为 y。总共有 四种 可能的情况可以分析，你可以通过跟踪电路来验证自己：

• x = 0 : 无论我们提供什么逆，输出将是 1。不管逆是否正确，我们并不在意，这与最后一个门 总是 yield 0 一致。
• x ≠ 0, y = x⁻¹ ≠ 0: 逆是正确的，输出是 0。最后一个门也应该 yield 0，这意味着逆是正确的。
• x ≠ 0, x⁻¹ = 0 : 逆是 不正确的。输出将是 1（这是 错误），而且最后一个门将 不 yield 0。因为最后的约束不成立，这意味着输入中的某些内容是错误的！
• x ≠ 0, y ≠ x⁻¹ ≠ 0: 逆是 不正确的，在这种情况下，输出将不 是1，而是有限域中的某 其他元素。因此，最后一个门肯定 不会 yield 0——这意味着提供的逆是错误的。

就是这样！我们的 零检查电路 完成了。

这些执行 简单任务 的简单元素在构建越来越大电路的过程中可发挥巨大作用。它允许某种程度的 组合性，从而可以显著加速电路的制作！

总结

这些只是你可以使用算术电路做的一些事情的例子：由于它们是如此通用的计算模型，你几乎可以构建任何类型的声明。

当然，如果我们必须自己拼凑很多门的话，创建电路本身可能会有点困难。这就是为什么我们 从来不真的这样做。

我们使用 其他类型 的表示，它们可以被 概念化 为电路。

Circom，一种流行的电路构建 DSL，不强迫你编写门。而是依赖于一种称为 算术化 的技术，将一组约束转换为适合 zkSNARKs 的形式。

最后，SNARKs 有许多好处（小证明大小，短验证时间），但也有一些引发的担忧（例如，Plonk 需要一个 可信设置）。出于这个原因（还有其他原因），这仍然是一个非常积极的研究领域。谁知道我们将来看见什么未来的内容！

讲到 可信设置 和理想中 避免它们，还有另一种不需要的简明知识证明——它是 透明的。因此，在我们冒险的下一章中，我们将探索 STARKs 的世界，它是 SNARKs 的小兄弟，带来了一些有趣的属性。期待 下一个！

• 原文链接： medium.com/@francomangon...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，在这里修改，还请包涵～