STARKs，第一部分：多项式的证明

特别感谢 Eli Ben-Sasson 的持续帮助、解释和审查，他提供了一些在本文中使用的示例，最重要的还是发明了这些东西；感谢 Hsiao-wei Wang 的审查

希望到现在为止，许多人都听说过 ZK-SNARKs，这是可以用于从可验证计算到隐私保护的加密货币各种用例的一种通用简洁的零知识证明技术。你可能不知道的是，ZK-SNARKs有一个更新、更闪亮的表亲：ZK-STARKs。ZK-STARKs中的“T”代表“透明”，它解决了ZK-SNARKs主要的一个弱点：对“受信任设置”的依赖。它们还提供了更简单的密码学假设，避免了椭圆曲线、配对和知识指数假设，而是完全依赖于哈希和信息理论；这也意味着它们即使针对量子计算机攻击者也依然安全。

然而，这也有代价：一个证明的大小从288字节增加到几百千字节。有时候成本不值得，但在许多情况下，尤其是在公共区块链应用中，需求信任最小化的情况下，这可能是值得的。而且如果椭圆曲线被破解或者量子计算机 确实 到来，成本就一定是值得的。

那么，这种另一种类型的零知识证明是怎么工作的呢？首先，让我们回顾一下通用简洁的ZKP做什么。假设你有一个（公共）函数f，一个（私有）输入x和一个（公共）输出y。你想证明你知道一个x，使得f(x)=y，而不泄露x是什么。此外，为了让证明是简洁的，你希望它的可验证性比计算f本身快得多。

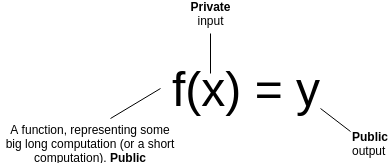
让我们来看几个例子：

• f是一个在普通计算机上运行两周的计算，但在数据中心上运行两个小时。你将计算（即运行f的代码）发送给数据中心，数据中心运行它，并返还答案y及证明。你在几毫秒内验证证明，并确信y确实是答案。
• 你有一笔加密交易，形式为“X1是我的旧余额。X2是你的旧余额。X3是我的新余额。X4是你的新余额”。你想创建一个证明，证明这笔交易是有效的（具体来说，旧余额和新余额都是非负的，我的余额减少抵消了你的余额增加）。x可以是一对加密密钥，f可以是一个函数，它将交易作为内置公共输入，作为输入密钥，解密交易，进行检查，并在通过时返回1，不通过时返回0。y当然是1。
• 你有一个像以太坊这样的区块链，你下载了最近的区块。你想要一个证明，以证明这个区块是有效的，并且该区块在一个每个区块都有效的链的顶端。你请求一个存在的全节点提供这样的证明。x是整个区块链（是的，所有?? GB的它），f是一个逐块处理它的函数，验证有效性并输出最后区块的哈希，y是你刚下载的区块的哈希。

那么，这一切有什么难的？原来，零知识（即隐私）保证是（相对而言！）相对容易提供的；有多种方法可以将任何计算转换为诸如三色图问题之类的实例，其中图的三着色对应于原问题的解决方案，然后使用传统的零知识证明协议证明你有有效的图着色，而不透露它是什么。这篇 Matthew Green 2014 年的优秀文章对此有详细描述。

提供简洁性则要困难得多。直观地说，简洁地证明关于计算的事情是困难的，因为计算是极其脆弱的。如果你有一个漫长且复杂的计算，而你作为一个邪恶的精灵有能力在计算的中间将0翻转为1，则在许多情况下，即使是翻转零的一个比特也足以使计算给出完全不同的结果。因此，难以通过随机抽样计算跟踪来判断其正确性，因为很容易错过那个“邪恶的比特”。然而，通过一些复杂的数学，我们实现这一点。

总体而言，这些完成者的协议使用与 擦除编码的类似数学，这种编码经常用于实现数据的容错。如果你有一段数据，并且你将数据编码为一条线，则你可以在这条线上挑选出四个点。任何两个点都足以重构出原始线段，因此也可以为你提供另外两个点。此外，如果你对数据进行即使是最小的更改，至少会保证有三个点。这些算法将在此过程中大量使用多项式进行错误放大。

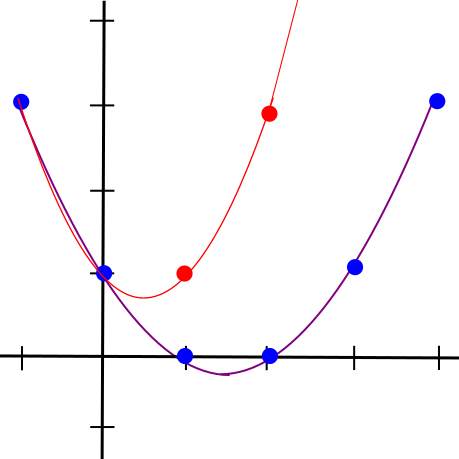
一个稍微简单的例子

假设你想证明你有一个多项式P，使得对于所有从1到100万的x，都有P(x)是一个满足0≤P(x)≤9的整数。这是“范围检查”中相当常见的简单实例；你可能会想象这种检查用于验证，例如，在应用一些交易集之后，一组账户余额是否仍然为正。如果它的条件是1≤P(x)≤9，这可能是检查这些值形成一个正确的数独解的一部分。

“传统”的证明方法是展示所有100万点，通过检查值来验证。然而，我们想看看是否能制作出一个可以在少于100万步中验证的证明。简单地随机检查P的评估是行不通的；始终有一个恶意证明者可能来制造一个在999,999个地方满足条件的P，但在最后一个地方不满足条件，而随机抽样只会错过那个值。那么，我们 能 做什么呢？

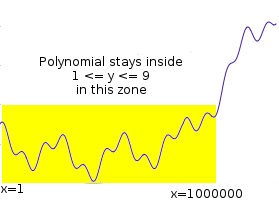
让我们在数学上稍微转换一下问题。设C(x)为约束检查多项式；如果0≤x≤9，则C(x)=0，反之非零。有一种简单的方法来构造C(x)：x⋅(x−1)⋅(x−2)⋅…(x−9)（我们假设所有的多项式和其他值仅使用整数，因此我们不需要担心中间的数字）。

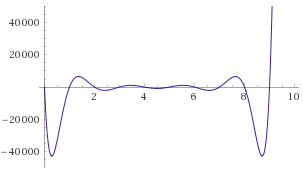
现在，问题变成了：证明你知道P使得C(P(x))=0对于1到1000000之间的所有x。设Z(x)=(x−1)⋅(x−2)⋅…(x−1000000)。一个已知的数学事实是，任何在所有1到1000000的x中等于零的多项式都是Z(x)的倍数。因此，问题现在可以再次转换：证明你知道P和D，使得对于所有x都有C(P(x))=Z(x)⋅D(x)（注意，如果你知道一个合适的C(P(x))，那么通过Z(x)对其进行除法以计算D(x)并不是太困难；你可以使用 长多项式除法 或更实际的基于 FFT 的更快算法）。现在，我们将原始陈述转换为一种看起来数学上清晰且可能可以证明的形式。

那怎样证明这个声明呢？我们可以将证明过程想象为证明者与验证者之间的三步通信：证明者发送一些信息，然后验证者发送一些请求，然后证明者发送更多信息。首先，证明者承诺（即建立一个Merkle树并将P(x)和D(x)对于1到10亿的所有x的评估值的根哈希发送给验证者）（是的，10亿）。这包括100万点在0≤P(x)≤9的情况下，以及990万点（很可能）不满足该条件的情况。

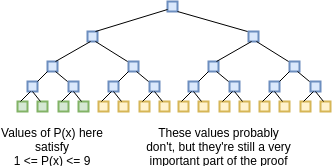
我们假设验证者已经知道这些点上Z(x)的评估；Z(x)就像这个方案的“公共验证密钥”，任何人都必须预先知道（没有足够空间存储Z(x)的客户端可以简单地存储Z(x)的Merkle根，并要求证明者提供验证者需要查询的每个Z(x)值的分支；另外，还有一些数域，对于某些x来说，Z(x)是非常容易计算的）。在收到承诺（即Merkle根）后，验证者选择1到10亿之间的16个随机x值，并要求证明者提供P(x)和D(x)在这些点的Merkle分支。证明者提供这些值，验证者检查：（i）分支与先前提供的Merkle根相匹配，以及（ii）在所有16个案例中C(P(x))实际等于Z(x)⋅D(x)。

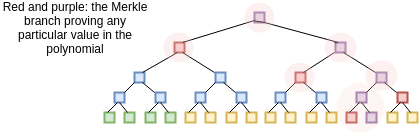
我们知道这个证明是完美完整的：如果你真的知道一个合适的P(x)，那么如果你计算D(x)并正确构造证明，它将始终通过16次检查。但是 soundness如何——也就是如果一个恶意的证明者提供一个错误的P(x)，他们被抓住的最低概率是多少？我们可以如下分析。因为C(P(x))是由一个10度多项式与一个10亿度多项式复合而成，因此其度最多为1000万。一般情况下，我们知道两个不同的N度多项式最多在N个点上会一致；因此，一个不等于永远等于Z(x)⋅D(x)的任何多项式的10,000,000度的多项式必然与所有点的结果在至少990,000,000个点上不一致。因此，坏的P(x)即使在一次检查中被抓住的概率已经达到99%；通过16次检查，被捕的概率提高到1−10−32；也就是说，这个方案的伪造的难度与计算哈希碰撞的难度相当。

那么......我们刚刚做了什么？我们利用多项式“放大”了任何错误解决方案中的错误，使得对原问题的任何不正确解决方案，其直接查找需要100万次检查，变成了验证协议的解决方案，能在99%情况下被标记为错误。

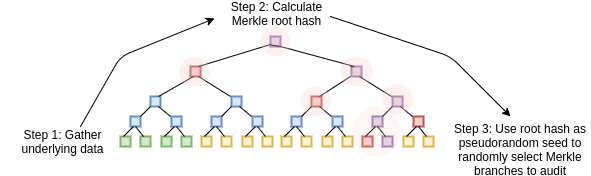
我们可以将这个三步机制转换为一个非交互式证明，这可以由一个单一的证明者一次性广播，然后由任何人验证，使用 Fiat-Shamir启发式。证明者首先构建P(x)和D(x)值的Merkle树，并计算树的根哈希。根本身然后用作决定证明者需要提供哪些树分支的熵来源。然后证明者将Merkle根和分支一起广播作为证明。所有计算在证明者端完成；从数据计算Merkle根的过程，以及使用其选择需要审计的分支，实质上取代了交互式验证者的需求。

没有有效P(x)的恶意证明者能做的唯一事情就是尽量一次次尝试生成有效的证明，直到最后在计算出的Merkle根选择的分支中 极其 幸运，但是，具有1−10−32的健全性（即失败的概率至少为1−10−32），这位恶意证明者需要数十亿年才能制作出一个可接受的证明。

更进一步

为了说明这种技术的强大，让我们用它做一些稍微不那么琐碎的事情：证明你知道第100万Fibonacci数。为了做到这一点，我们将证明你知道一个表示计算磁带的多项式，其中P(x)表示第x个Fibonacci数。约束检查多项式现在将在三个x坐标上跳动：C(x1,x2,x3)=x3−x2−x1（注意，如果C(P(x),P(x+1),P(x+2))=0对于所有x成立，则P(x)表示Fibonacci序列）。

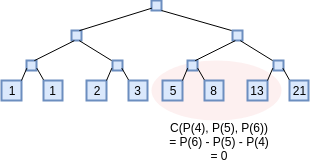
翻译后的问题变成：证明你知道P和D，使得C(P(x),P(x+1),P(x+2))=Z(x)⋅D(x)。对于证明审计的16个索引，证明者需要提供P(x)，P(x+1)，P(x+2)和D(x)的Merkle分支。证明者还需要提供Merkle分支以显示P(0)=P(1)=1。否则，整个过程都是一样的。

现在，现实中实现这一点要解决两个问题。第一个问题是，如果我们实际尝试与常规数字一起工作，解决方案在实践中将不够高效，因为数字本身很容易变得极大。例如，第100万Fibonacci数有208988位数字。如果我们想在实践中实现简洁性，我们需要使用有限域——一种数字系统，依然遵循我们知道和喜爱的算术法则，比如a⋅(b+c)=(a⋅b)+(a⋅c)和(a2−b2)=(a−b)⋅(a+b)，但每个数字保证占用一个恒定的空间。证明关于第100万Fibonacci数的声明将需要更复杂的设计，该设计在这个有限域数学的基础上实现大数算术。

最简单的有限域是模运算；即用某个素数N替换每个实例的a+b为a+bmodN，对减法和乘法也这样做，而对于除法使用 模逆（例如，如果N=7，则3+4=0，2+6=1，3⋅4=5，4/2=2以及5/2=6）。你可以通过我关于素数域的描述 了解更多（在页面中搜索“素数域”）或这篇关于模块算术的 维基百科文章（直接搜索“有限域”和“素数域”的文章往往非常复杂，直接进入抽象代数，最好不要打扰）。

第二，你可能注意到在我上述关于健全性的证明草图中，我忽略了覆盖一种攻击：如果攻击者承诺一些不在任何相对低度多项式的值，而不是令人信服的1,000,000度的P(x)和9,000,000度的D(x)呢？那么，关于无效的C(P(x))必须在至少990百万个点上与任何有效的C(P(x))相区别的论证便不适用，因此可能会出现不同的、更有效的攻击。例如，攻击者可以为每个x生成一个随机值p，然后计算d=C(p)/Z(x)并承诺这些值，以替代P(x)和D(x)。这些值将不会在任何低度多项式上，但它们 会 通过测试。

事实证明，这种可能性可以有效防御，尽管实现的方法相当复杂，因此你可以合理地说，STARKs的数学创新大部分由此构成。此外，解决方案还有限制：你可以排除对 非常 远离任何1,000,000多项式的数据的承诺（例如，你需要更改20%的所有值才能使其成为一个1,000,000度多项式），但你无法排除对仅在一个或两个坐标上与多项式不同的数据的承诺。因此，这些工具所提供的将是近似证明——证明P和D上的大多数点对应于正确的多项式。

事实证明，这足以构建一个证明，尽管有两个“附加条件”。首先，验证者需要检查更多的索引，以弥补这种限制引入的额外错误空间。其次，如果我们进行“边界约束检查”（例如，在上述Fibonacci示例中验证P(0)=P(1)=1），那么我们需要扩展近似证明，证明这两个特定点（或任何其他你想检查的特定点数量）确实在那个多项式上。

在本系列下一部分中，我将更详细地描述近似检查的解决方案，而在第三部分中，我将描述如何构建出更复杂的约束函数，以检查不仅仅是Fibonacci数和范围的任意计算。

• 原文链接： vitalik.eth.limo/general...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～