ECDSA上的适配器签名

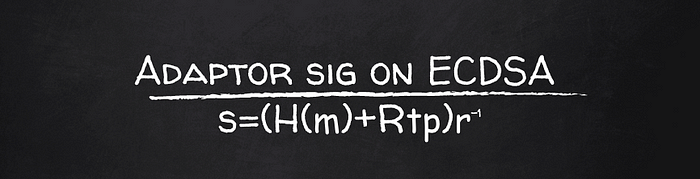
适配器签名系列:

1.适配器签名 - Schnorr签名和ECDSA- 2.Schnorr上的适配器签名 - 跨链原子交换- 3.Schnorr上的适配器签名 - 闪电网络- 4.ECDSA上的适配器签名 5.ECDSA上的离散对数合约中的适配器签名

前面的章节描述了基于Schnorr签名的适配器签名构造，这些构造目前在比特币主网上无法使用。

目前，比特币中只能使用ECDSA，而且由于ECDSA方程不是线性的（包含r-1项），因此无法通过简单地将多个签名相加来创建多方签名。（详见第一章“适配器签名 - Schnorr签名和ECDSA-”）

虽然已经提出了两方ECDSA签名协议和适配器签名构造，但它们依赖于复杂的密码学和额外的安全假设，使得在实践中难以使用。

幸运的是，有一种优雅的提案用于两方ECDSA适配器签名。该提案利用OP_CHECKMULTISIG来替代上述协议的复杂性，仅通过简单的比特币脚本操作实现。虽然这样做减少了隐私性，因为OP_CHECKMULTISIG本身在交易中是可见的，但适配器签名中使用的秘密值t不能被任何第三方获取。我们将这种方法称为“半无脚本”。本章将重点介绍“ECDSA上的半无脚本协议”。

1–1.ECDSA适配器签名和解密
与Schnorr签名不同，ECDSA适配器签名是通过乘法而不是加法进行调整的。这是因为ECDSA方程不是线性的。

1–2.ECDSA适配器签名验证

为了在不了解秘密值t的情况下验证ECDSA适配器签名，我们使用了一个额外的点R’= Rt ​​= rT。这里，R’被定义为一个椭圆曲线点，通过将点T乘以标量r生成。

然而，第三方无法验证它是否是通过R’= rT创建的（他们不知道r）。为了证明这种关系，我们使用了离散对数等价证明（DLEQ）。

1–3.DLEq

DLEQ证明的目标是让证明者说服验证者两个元素在两个不同的生成器下具有相同的离散对数，而不暴露离散对数是什么。这正是我们需要的，以确保R和R’确实是相关的，并且是使用相同的秘密t生成的。换句话说，这个证明将表明使用了相同的r值来生成两者。

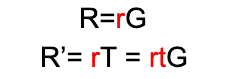
该证明遵循标准的知识证明结构，分为三个阶段：

1. 证明方（证明者）首先选择一个随机数r2，并向验证方（验证者）提供值R2=r2*G和R2’=r2*T。这部分协议称为承诺，因为证明者通过在组G和T中提供其图像来承诺一个随机值。

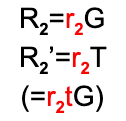
2. 验证者选择一个随机值e并将其发送回证明者。这部分协议称为挑战，因为验证者用一个随机值对证明者进行挑战。

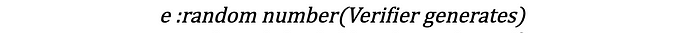
3. 证明者计算s，并将该值发送回验证者。

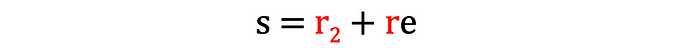
4. 验证者检查：

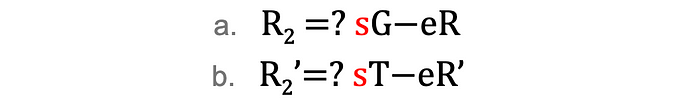
现在让我们尝试理解这个协议是如何工作的。首先，你应该注意到步骤3中的方程。这与Schnorr签名的方程相同！因此，证明者正在向验证者发送一个Schnorr签名，覆盖由验证者选择的消息。如果这个签名有效，验证者可以确定证明者知道值r。然而，回想一下，我们的目标是确保R’=t*R(=r*t*G)。这就是为什么验证者执行两个检查。让我们看看这些检查以更好地理解。

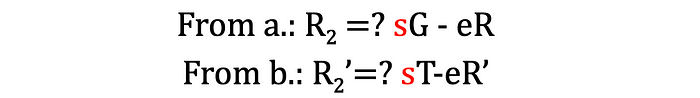
请注意，如果这两个方程成立，它们之间必须存在线性关系，事实上这种关系就是t：

然而，这里提出的证明有一个缺点，即证明者和验证者之间需要互动。幸运的是，存在一种机制，即所谓的Fiat-Shamir变换，它能够将一个互动证明转换为非互动证明。这是以一个额外的安全假设为代价的，该假设假定存在一个真正的随机函数，该函数为每个唯一的查询返回一个不同的（且均匀选择的）值（这是著名的“随机预言模型”）。在实际操作中，对于我们的证明，这意味着通过要求证明者提交e值来替换挑战部分，该值使用哈希函数构造如下：

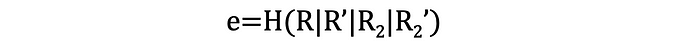
这背后的直觉是，证明者很难（在实践中不可能）选择初始的r和r2值，使得这个哈希的结果不会是随机值。

回到ECDSA适配器签名，它们必须由s’、R和R’值组成，并且包含一个非互动的DLEQ证明，以便接收者可以验证R和R’实际上是相关的。

通过学习这种方式，我们已经学会了通过证明离散对数的等价性来验证ECDSA上的多方适配器签名。

在下一篇文章中，我们将讨论ECDSA上的基于适配器签名的DLC，并深入细节。

参考资料：

无脚本脚本(2017年5月,Andrew Poelstra)

简单的Schnorr多重签名及其在比特币中的应用(2018,Gregory Maxwell, Andrew Poelstra, Yannick Seurin2,Pieter Wuille)

快速安全的两方ECDSA签名(2017,Yehuda Lindell)

基于ECDSA的无脚本脚本(2018年4月,Pedro Moreno-Sanchez, Aniket Kate)

无需2p-ECDSA或Schnorr的支付点(2019年10月,uSEkaCIO)

一次性可验证加密签名 即适配器签名(2019年10月,Lloyd Fournier)

Stack Exchange Q.我们如何证明两个离散对数相等？

• 原文链接： medium.com/crypto-garage...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～