Uniswap V3 详解
Q 数字格式 - Solidity 编程
- RareSkills
- 发布于 2025-02-21 13:40
- 阅读 2543
本文详细介绍了在Solidity中使用Q格式表示定点数的方法,包括Q数的定义、表示方式、转换方法以及在Solidity中的实际应用示例。文章还对比了Q数与以太坊中的十进制表示,指出了Q数在乘除运算中的高效性。
Q 数字格式是一种表示二进制 定点数字 的符号。
定点数字是 Solidity 中一个流行的设计模式,用于存储分数值,因为该语言不支持浮点数。因此,为了“捕获”数字的小数部分,我们通过一个整数乘以这个分数,以使得小数部分变成整数(有可能会有一些精度损失)。
Ether 小数与 Q 数字
Solidity 编程中最著名的定点数字是“一 Ether”。一 Ether 实际上是 10^18 个基本单位(Wei)。“一” Ether 实际上是 1 次 10^18 的结果。由于我们无法在 Solidity 中存储 “0.5”,因此我们改为存储 0.5×10^18=5×10^17 或 500000000000000000。本质上,10^18 乘以 0.5,以便小数部分能够“保留”为一个整数。然而,这并不是一个完美的解决方案,因为它无法存储小于 10^-18 的值。然而,10^18 对于大多数应用来说已经足够,并且如果需要更多的精度,合约可以使用更大的数字。
另一方面,Q 数字将分数乘以 2 的幂,而不是 10 的幂,因为在 EVM 中,通过 2 的幂进行乘法(和除法)更节省 gas,因为乘法或除法可以使用位移操作。例如,x << n 相当于 x * 2**n,而 x >> n 相当于 x / 2**n。
Q 数字表示法
Q 数字通常写作 Qm.n,其中 n 是用于乘以数字的 2 的幂,而 m 是整数部分的无符号整数大小。这完全等同于说 m 是用于存储整数部分的位数,而 n 是用于存储小数的位数。
为了演示这种等价性,考虑一个 Q1.1 数字。这个数字为整数部分分配 1 位(m = 1),为小数分配 1 位(n = 1)。数字 1 被表示为 1×2^1,这相当于 1 << 1。1×2^1 或 1 << 1 的二进制表示为 10。注意我们的数字是 2 位长(n+m=2)。我们可以将 10₂ 拆解为:

因此,存储“1”的 Q1.1 变量实际上存储的值是 2,或者二进制 10₂。然而,如果用于存储一个 Q1.1 的变量,我们会“解释”或“处理”这个值 2 为 1。
让我们来看一个 Q8.4 数字的例子。数字 1 被表示为 1×2^4 或 1 << 4。 1 << 4 的二进制表示为 10000₂。因为我们有 8 位表示整个数字部分,我们需要用零填充,直到整个数字有 12 位:

总共有 12 位存储这个数字,因为 8 + 4 = 12。“在底层”,我们实际上存储的值是 2^4=16,但我们将变量值解释为 1。这和我们可能将变量解释为持有“1 Ether”但是“在底层”变量实际上存储 10^18 是类似的。当我们说“在底层”时,我们指的是内存或存储中的实际数字。
作为第三个例子,考虑一个 Q4.8 数字。数字 1 被表示为 1×2^8 或 1 << 8。1 << 8 的二进制表示为 10000000₂。因为我们有 4 位表示整数部分,我们用三个零填充,直到整个数字有 12 位:

Q4.8 和 Q8.4 数字都需要 12 位来存储。然而,Q8.4 数字为整数部分分配了更多的位,因此它可以存储更大的整数。另一方面,Q4.8 数字为小数部分分配了更多的位,因此它在表示分数方面可以更精确。
数值“1”作为定点数字
一般来说,对于 Q 数字,“1”是 1 乘以 2^m,其中 m 是存储小数的位数。因此,Q64.96 中的 1 是 1×2^96 或 1 << 96。“在” Q128.128 中的“1”是 1×2^128 或 1 << 128。 Q64.128 中的“1”也是 1 << 128,因为我们只关心小数位的数量。
对于 任何 Qm.n,整数 1 的表示形式总是 1 << n,而且恰好 两个 Q64.128 和 Q128.128 的 n = 128。
请注意,n 表示 二进制 位数(底数 2),而不是“十进制数”的数量,如十的幂(底数 10)。Qx.18 不是我们用 10^18 来存储 1 ether 的方式。Qx.18 意味着“1”是 1×2^18,而不是 1×10^18。
在 Solidity 中使用 Q 数字
Qm.n 数字中的位数必须大于或等于 m + n 位。因此:
- Q64.64 数字至少必须使用 uint128(128 = 64 + 64)
- Q64.96 数字至少必须使用 uint160(160 = 64 + 96)
- Q128.128 数字必须使用 uint256
解释 Q 数字的小数部分
让我们考虑所有可能的 Q1.1 数字的值:
| “在底层”的值 | 浮点值(“在底层” ÷ 2^1) | |
|---|---|---|
| 0 0 | 0 | 0 |
| 0 1 | 1 | 0.5 |
| 1 0 | 2 | 1.0 |
| 1 1 | 3 | 1.5 |
我们可以看到“分数位”被设置为 1 表示分数部分的单个位代表值 0.5。一般来说,分数位代表二的分数幂。让我们来看一个 Q1.2 数字的例子:
| “在底层”的值 | 浮点值(“在底层” ÷ 2^2) | |
|---|---|---|
| 0 00 | 0 | 0 |
| 0 01 | 1 | 0.125 (1/4) |
| 0 10 | 2 | 0.5 (2/4) |
| 0 11 | 3 | 0.75 (3/4) |
| 1 00 | 4 | 1.00 (4/4) |
| 1 01 | 5 | 1.25 (5/4) |
| 1 10 | 6 | 1.50 (6/4) |
| 1 11 | 7 | 1.75 (7/4) |
一般来说,Q 数字中的位按如下方式解释。注意小数点右边的位表示二的分数幂:
…1111.1111……8421.121418116…
每个位在加法上代表一个二的分数幂。例如, 0.1₂ 代表 0.5, 0.11₂ 代表 0.75, 0.001₂ 代表 0.125 或二分之一。
Q 数字只能编码可以表示为 1 除以 2 的幂的分数。如果我们尝试表示像 1/3 这样的数字,必须会存在舍入误差。
尝试将各种分数值插入以下交互工具,看看它们是如何转换为定点表示的:
定点数字演示
Q4.4 定点数字演示
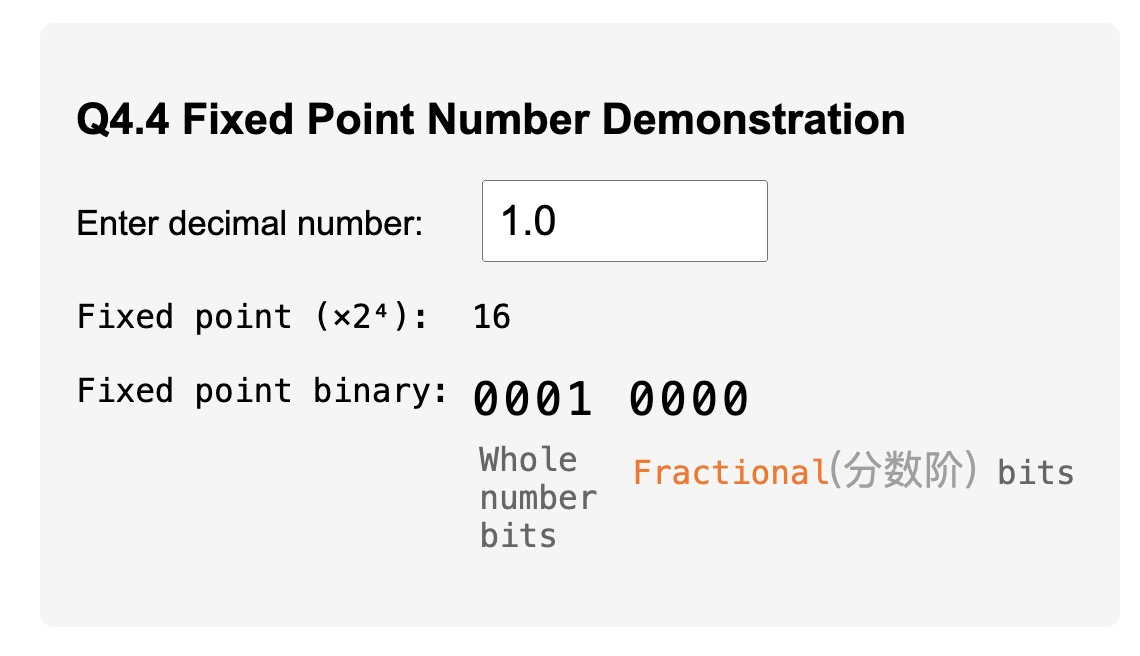 输入十进制数:
输入十进制数:
定点(×2⁴):16
定点二进制:0001 0000
将整数转换为 Q 数字
要将 整数 1 转换为 Q64.96 定点数字,我们计算 1 << 96。这在第 96 位创建一个带有 1 的二进制数字,并且在二进制值 0 到 95(包括 0 到 95)上是 0。
一般来说,可以通过将整数左移 n 位将其转换为 Qm.n 数字。
下面的动画演示了这一点:
https://img.learnblockchain.cn/2025/02/25/IntegerToQ44c.mp4
将 Q 数字转换为整数
Q 数字有一个小数部分,但整数没有。因此,要将一个 Q 数字转换为整数,我们只需将整数部分右移,使小数部分被移除。
因此,如果我们想提取定点数字的整数部分,我们右移数字 n 位(记住:n 是 Qm.n 中的小数位的数量)。这样就会导致小数位消失,只剩下整数部分。换句话说,我们通过切掉所有的小数位,将一个定点 Q 数字转换为一个整数。
考虑将 Q4.4 数字转换为整数的以下动画:
https://img.learnblockchain.cn/2025/02/25/Q44ToInteger.mp4
构造定点值
假设我们想将数字“1.5”编码为 Q64.96。Solidity 不接受 1.5 * 2**96 或 1.5 << 96 作为有效的语法。
相反,1.5 可以这样计算:
1 * 2**96 + 2**96 / 2; // 相当于 1 + 0.5存储在 Q64.96 数字中的“在底层”的值为 118842243771396506390315925504。我们可以在 Python 中计算这个值:
>>> int(1.5 * 2**96)
118842243771396506390315925504在二进制中,我们可以看到 96 位用于小数:
>>> bin(118842243771396506390315925504)
'0b1 100000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000' # 为了清晰添加了空格将 Q 数字转换为浮点数字(离线)
使用我们之前的例子 1.5,我们可以将 118842243771396506390315925504 除以 2^96并得到
118842243771396506390315925504 / 2^96 = 1.5
当我们计算一个 Q 数字在离线环境中的浮点值时,我们使用 118842243771396506390315925504 除以 2^96,而不是右移 96。因为位移操作会“毁坏”右边的 96 位,所以包含小数的信息就会丢失。
Q 数字可以存储的最大值
Q 数字可以存储的最大 整数 值为 2^m−1,其中 m 是整数部分的位数。它可以存储的最大 总值 是最大整数部分加上最大可表示分数:
∑i=1n=12+14+⋯+12n
这是数学上等同于 $1-\frac{1}{2^n}$ 。因此,最大 总 值 Qm.n 数字可以存储为 2^m−1 * 2^n。
例如,Q96.64 的最大 整数 值是 2^96−1,即 79228162514264337593543950335。整个 Q96.64 值可以存储的最大值(包括小数部分)为:
(2^96−1)+(1−1/2^64)
或者
79228162514264337593543950335.9999999999999999999457898913757247782996273599565029144287109375
将两个 Q 数字相加
如果我们想将例如一个 Q128.128 数字与一个 Q64.64 数字相加,我们有两个选项。第一个选项是将 Q64.64 数字左移 64 位,以便小数点对齐。这有效地将 Q64.64 数字转换为 Q64.128 数字。
或者,我们还有第二个选项。如果我们不需要 128 位的精度,或者我们特别想要一个 Q64.64 数字作为和,我们可以将 Q128.128 数字右移 64 位,这将其转换为 Q128.64 数字。当然,这会导致一些精度损失。
要将两个 Q 数字相加,我们只需要它们在小数部分具有相同数量的位,即小数点必须对齐。然而,“目标”数据类型必须有足够大的整数量部分来处理和,否则可能会有溢出。
如果我们想要相减两个 Q 数字,我们也遵循本节中列出的相同逻辑。
乘法或除法
如果我们将 1×1 进行乘法,我们希望得到 1 作为答案。然而,在底层,数字 1 是用 2^96 表示的。因此,如果我们将以 Q64.96 表示的数字 1 乘以自己,实际上就是在执行运算 2^96×2^96=2^192,但我们实际上想要的答案是 2^96。
因此,当我们将两个 Q 数字相乘时,我们必须随后将乘积右移 n 位。在我们 96 位的例子中,这意味着 2^192 会右移 96 位,得到的结果为 2^96。
一些 Solidity 定点数例子
示例 1:将 5 除以 2
假设我们想将 5 除以 2,并将结果返回为一个 Q64.64 数字。由于 Q64.64 不支持大于 64 位的整数,我们可以使用 uint64 来表示整数 5 和 2。事实上,持有一个 Q64.64 需要 128 位,因此我们将使用 uint128 来存储 Q64.64。
换句话说,这些整数使用 uint64 表示,因为这是 Q64.64 能够存储的最大整数,但是 Q64.64 数字用 uint128 表示,因为它需要为整数存储 64 位和小数存储 64 位。
function divToQ64x64(uint64 x, uint64 y) public pure returns (uint128) {
// 将 x(一个 uint64 整数)
// 通过左移 64 位转换为一个 Q64.64 定点数字。
uint128 x64_64 = x << 64;
// 除以 y
return x64_64 / y;
}
divToQ64x64(5, 2); // 返回 46116860184273879040结果 46116860184273879040 编码为 2.5,因为 46116860184273879040 / 2^64 = 2.5。
示例 2:将 5 乘以 0.5
让我们将 5 与 0.5 相乘,二者均表示为 Q64x64。其表示如下:
- 5 作为 Q64.64 数字表示为
5 << 64或5 * 2^64,等于 92233720368547758080。 - 0.5 作为 Q64.64 数字表示为
1 << 64 / 2或2^64 / 2,等于 9223372036854775808
当我们将两个定点数字相乘时,我们需要确保它们在我们再次除以 2^64 之前不会溢出。这意味着我们将乘积存储在一个 uint256 中然后右移 64 位。
function mulU64x64(uint128 x, uint128 y) public pure returns (uint128) {
// 注意:Solidity 以 uint128 执行乘法,除非
// 显式转型。这可能会溢出并发生回退。
uint256 temp = uint256(x) * uint256(y);
return uint128(temp >> 64);
}
mulU64x64(5 * 2**64, 2**64 / 2) // 返回 46116860184273879040这将返回预期的结果,因为 46116860184273879040 / 2^64 = 2.5。
示例 3:将 5 乘以 0.5,但 5 是一个整数而非定点
作为上述示例的变体,我们希望将 5(一个整数)乘以 0.5(一个定点数字)并返回一个定点数字。唯一与上面代码的不同之处在于将 5 转换为其定点表示:
function mulUint64ByQ64x64(uint64 x, uint128 y) public pure returns (uint128) {
// 将 uint64 转换为定点
uint128 x_fp = uint128(x) << 64;
uint256 temp = uint256(x_fp) * uint256(y);
return uint128(temp >> 64);
}
mulUint64ByQ64x64(5, 2**64 / 2) // 返回 46116860184273879040结果仍然是 2.5 的定点等效值。
左移 64 位然后右移确实有点浪费。可以更有效地完成相同的计算,如下所示:
function mulUint64ByQ64x64(uint64 x, uint128 y) public pure returns (uint128) {
return uint128(uint256(x) * uint256(y));
}
mulUint64ByQ64x64(5, 2**64 / 2) // 返回 46116860184273879040除法 Q 数字
如果我们计算 1 ÷ 1,我们希望结果为 1。假设我们使用 Q64.64。“1” 是 2^64。如果我们计算 2^64÷2^64,我们得到的结果是 1,而不是 2^64。为了解决此问题,我们可以将结果左移 n 位,但这违反了“为了避免精度损失,应先乘后除”的原则。因此,两个 Q 数字的正确除法方法是先左移分子,然后再进行除法:
function divQ64x64ByQ64x64(uint128 x, uint128 y) public pure returns (uint128) {
return uint128(uint256(x) << 64 / uint256(y));
}
divQ64x64ByQ64x64(5, 2**64 / 2) // 返回 46116860184273879040总结
- Q 数字是一种在 Ethereum 中保存分数数字的设计模式。
- 与以太坊十进制表示相比,它们更高效,因为乘法和除法可以通过位移来完成。
- Q 数字表示为 Qm.n,其中
m是整数的位数,n是小数的位数。 - 小数点之后的每一位表示的值为 1/2, 1/4, 1/8, … 等等。
- 整数可以通过左位移
n位转换为 Q 数字。Q 数字可以通过截断小数位或右移n位转换为整数。 - 如果我们将 Q 数字除以 2^n 在支持浮点的语言中,我们可以看到预期的分数表示。
- 给定两个整数
a和b,确保a适合于m位。通过a << n / b计算其比率为 Qm.n 数字。用于保存结果定点数字的位数必须是a的位数 (m) 加上n,即 Qm.n。 - Q 数字可以直接相加,只要小数点对齐。
- 如果我们将两个 Q 数字相乘,我们需要将结果左移
n位,以便结果具有n个小数。 - 如果我们将两个 Q 数字相除,我们需要首先左移分子
n位。 - 在除法和乘法中都需要小心,以避免临时溢出。
- 原文链接: rareskills.io/post/q-num...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
