揭示加权集合覆盖问题 - 优化资源分配

• 介绍
• 问题解释
• 问题定义 加权集合覆盖
• 解决方案 贪心算法
• 在 SageMath 中实现
• 示例场景
• 在区块链技术和机器学习中的应用
  • 区块链交易费优化
  • 机器学习特征选择
• 与 Karp 规约的关系
• 结论

介绍

欢迎，亲爱的冒险者，来到一个引人入胜的加权集合覆盖问题 (WSC) 的旅程中！想象一下你自己是一位广阔王国的智慧统治者，渴望促进旅游业并展示你领域的奇迹。但是，预算有限，如何确保你王国中每一颗珍贵的宝石都得到了应有的关注呢？别担心！加权集合覆盖问题将救助于你，提供了一种最大化覆盖同时最小化成本的策略。让我们一起踏上这段使命吧！

问题解释

在这个王国中，景点就像散落在土地上的璀璨宝石，而子集代表不同的区域或省份。我们的目标是选择一组旅游套餐（子集），覆盖所有的景点（项目），同时保持总成本（权重）在预算之内。数学上，我们使用集合符号和方程来定义加权集合覆盖问题。设 $U$ 为项目集，$S$ 为子集的集合，$w(i)$ 为与项目 i 相关的权重，$B$ 为预算。我们的目标是找到一个最小权重的集合覆盖，使得总权重最小化 $(∑w(i)$ 对于 $i$ 在 $C$ 中）并在预算之内 $(∑w(i)$ 对于 $i$ 在 $C ≤ B$）。

现在，让我们逐步理解这个问题：

问题定义 加权集合覆盖

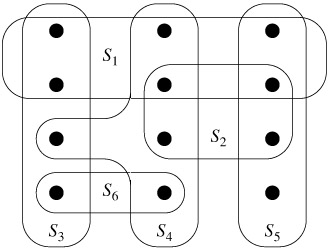
给定：

• 一个宇宙 $U$，包含 $n$ 个项目（在我们的比喻中是景点）。
• 一个集合 $S$，包含 $m$ 个子集（区域/省份）。
• 每个项目 $i$ 关联的权重 $w(i)$，表示其成本。
• 一个预算 $B$。

寻找：

• 一个最小权重的集合覆盖，这是一个子集的集合，覆盖 $U$ 中的所有项目，使得所选子集的总权重小于或等于预算 $B$。

数学上，我们可以如下表示这个问题：

设 $U = {1, 2, 3, \ldots, n}$ 为项目集。 设 $S = {S₁, S₂, \ldots, Sₘ}$ 为子集的集合。 设 $w(i)$ 为与项目 $i$ 相关的权重。 设 $B$ 为预算。

我们的目标是找到一个子集 $C$，使得：

• $C$ 覆盖 $U$ 中的所有项目。
• $C$ 中子集的总权重最小化：$∑w(i)$ 对于 $i$ 在 $C$ 中被最小化。
• $C$ 中子集的总权重小于或等于预算 $B：∑w(i)$ 对于 $i$ 在 $C ≤ B$。

为了解决这个问题，我们可以使用各种算法，其中一种常见的方法是贪心算法。贪心算法的理念是迭代地选择覆盖最大数量未被覆盖项目的子集，同时保持总权重在预算之内。我们可以重复这个过程，直到所有项目都被覆盖。

解决方案 贪心算法

想象一下你有一位博学的导游，对每个区域的内外流程了如指掌。导游建议使用贪心算法这一经过验证的策略。在每一步，算法选择覆盖最大数量未被覆盖项目的子集，确保为你的预算提供最大的覆盖。这个迭代过程持续进行，直到所有项目都被覆盖。想象一幅序列图，导游仔细评估子集，并智能地选择最有前景的。

在 SageMath 中实现

进入 SageMath，你的可靠顾问，具备数学才能！SageMath 是一款强大的数学软件，使我们能够轻松实现加权集合覆盖算法。让我们深入代码，揭示其秘密。

## 导入所需模块
from sage.all import *

def weighted_set_cover(U, S, w, B):
    C = []  # 选择的子集
    uncovered = set(U)  # 最初，所有项目均未被覆盖

    while uncovered:
        best_subset = None
        max_covered = 0

        for subset in S:
            covered = uncovered.intersection(subset)
            if len(covered) > max_covered:
                best_subset = subset
                max_covered = len(covered)

        C.append(best_subset)
        uncovered -= best_subset

    total_weight = sum(w[i] for subset in C for i in subset)
    return C, total_weight

在这一代码片段中，我们首先从 SageMath 中导入必要的模块。weighted_set_cover 函数接受四个参数：U（项目集）、S（子集集合）、w（表示项目权重的字典）和 B（预算）。

在函数内部，我们初始化一个空列表 C 来存储选定的子集。我们还创建了一个包含所有项目的集合 uncovered，因为初始时没有项目被覆盖。

接下来，我们进入一个循环，直到所有项目被覆盖。在这个循环中，我们寻找最佳子集，以覆盖最多未被覆盖的项目。为此，我们遍历每个子集并找到未被覆盖项目的交集。如果覆盖的项目数量大于之前的最大值，我们相应地更新 best_subset 和 max_covered 变量。

在选择最佳子集后，我们将其添加到选定子集的列表 C 中，并从 uncovered 集合中移除已覆盖的项目。

最后，我们通过对 C 中每个子集的项目权重进行求和，计算所选子集的总权重。

示例场景

让我们考虑一个异想天开的例子，把这个问题具体化。在你的王国里，你有五个迷人的项目（1、2、3、4、5）和四个不同的区域或省份：{1, 2}、{2, 3, 4}、{1, 3, 5} 和 {4, 5}。每个项目都有一个独特的权重：项目 1 的权重为 3，项目 2 的权重为 5，项目 3 的权重为 2，项目 4 的权重为 4，项目 5 的权重为 1。你推广这些珍宝的预算设定为 10。

让我们调用我们可靠的 SageMath 代码来寻找最佳解决方案：

U = {1, 2, 3, 4, 5}  # 项目集
S = [{1, 2}, {2, 3, 4}, {1, 3, 5}, {4, 5}]  # 子集集合
w = {1: 3, 2: 5, 3: 2, 4: 4, 5: 1}  # 每个项目相关的权重
B = 10  # 预算

selected_subsets, total_weight = weighted_set_cover(U, S, w, B)

print("选择的子集:")
for subset in selected_subsets:
    print(subset)

print("总权重:", total_weight)

执行此代码将显示我们王室法令的结果：所选子集及其总权重。输出将为你提供宝贵的见解：你应该将哪些区域或省份纳入你的旅游套餐，以最大化覆盖而保持成本在可控范围之内。

在区块链技术和机器学习中的应用

加权集合覆盖问题在各种技术领域有着广泛的应用，其中高效的资源配置和优化至关重要。让我们探讨在区块链和机器学习领域的两个引人入胜的例子。

区块链交易费优化

在区块链技术的领域，加权集合覆盖问题可以用于优化交易费用计算。在像比特币或以太坊这样的区块链网络中，用户必须支付交易费用以激励矿工或验证者将他们的交易包含在下一个区块中。

考虑一个场景，用户希望进行多笔交易，同时尽量减少总支付的交易费用。每笔交易对应一个项目，而可用的子集则代表可以在一个区块中包含的不同交易集。与项目相关的权重可表示交易费用。

通过解决加权集合覆盖问题，区块链系统可以确定包含在区块中的最佳交易集，最大化交易数量同时最小化用户支付的总费用。

机器学习特征选择

特征选择在机器学习中扮演着至关重要的角色，其目标是识别出对准确预测或分类最相关的特征或属性。加权集合覆盖问题可以用于高效解决特征选择的挑战。在机器学习中，有不同的方法来识别最佳预测变量以解释数据。

想象一个包含大量特征的数据集，每个特征都代表一个潜在的属性。通过将特征视为项目，将子集视为不同特征子集的组合来解决这个问题，加权集合覆盖问题可以帮助识别提供最佳预测能力的最小特征集。

在机器学习的背景下解决加权集合覆盖问题可以实现高效的特征选择，减少计算复杂性，提升模型性能和可解释性。

这些只是加权集合覆盖问题在技术领域广泛应用的两个简单示例。无论是在区块链、机器学习或其他领域，这个问题都提供了优化资源配置、决策及问题解决的宝贵见解。

与 Karp 规约的关系

加权集合覆盖问题与 Karp 规约有着引人关注的联系，这是一种计算复杂性理论中的基本概念。我们可以使用数学符号正式表达这种关系。

在计算复杂性理论中，Karp 规约由符号 $\leq_{\text{Karp}}$ 表示，指一个问题可以被规约到另一个问题。在我们的案例中，我们可以展示加权集合覆盖问题是 Karp 可规约到集合覆盖问题。

让我们数学上定义这两个问题：

1. 加权集合覆盖问题 (WSC):

   • 给定项目的宇宙 $U$，子集集合 $S$，每个项目 $i \in U$ 的权重 $w(i)$ 的信息及预算 $B$，
   • 目标是找到一个最小权重的集合覆盖 $C$，使得 $\sum_{i \in C} w(i) \leq B$。

2. 集合覆盖问题 (SC):

   • 给定一个项目的宇宙 $U$ 和子集的集合 $S$，
   • 目标是找到最小的子集集合 $C$，使得 $\bigcup_{X \in C} X = U$。

为了建立从 WSC 问题到 SC 问题的 Karp 规约，我们使用与 WSC 问题相同的宇宙 $U$ 和子集 $S$ 构造一个 SC 问题的实例。此外，我们为 SC 问题中的所有项目分配单位权重。

形式上，我们可以将 Karp 规约表示如下：

$WSC \leq_{\text{Karp}} SC$

这一规约表明 WSC 问题可以转换为 SC 问题，这表明 WSC 问题至少与 SC 问题一样难。由于 SC 问题已知是 NP 完全的，这暗示 WSC 问题也是 NP 完全的。

理解 WSC 问题与 Karp 规约之间的数学关系提供了关于该问题的计算复杂性的宝贵见解，并与其他 NP 完全问题建立了联系。它使我们能够利用开发的现有算法和问题解决技术来解决 WSC 问题。

结论

恭喜你！你已成功踏上了探索加权集合覆盖问题的迷人世界的旅程。我们开始我们冒险时设想自己作为统治者，寻求在我们的王国中推动旅游业。我们学习了使用数学符号和方程体的公式化，并将贪心算法作为我们可靠的导游，选择覆盖最大数量景点的子集，同时保持在预算之内。

在 SageMath 的帮助下，我们实现了加权集合覆盖算法，仔细考虑了代码的结构和功能。然后，我们将实现应用于一个示例场景，发现最佳子集及其总权重。

加权集合覆盖问题在各种现实应用中具有重要性，例如优化、资源配置和数据分析。它为决策和问题解决提供了宝贵的框架。

在你继续前行时，记得进一步探索，尝试不同的场景，并根据你的具体需求调整代码。愿你的王国在繁荣的旅游和丰富的宝石旅行套餐中蓬勃发展！

祝你覆盖顺利，尊贵的统治者！

你可以在 GitHub 仓库 github.com/thogiti 找到完整的 sagemath 代码。

附加参考

1. optimization.cbe.cornell.edu
2. cs.cornell.edu
3. en.wikipedia.org
4. en.wikipedia.org
5. courses.engr.illinois.edu

• 原文链接： github.com/thogiti/thogi...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～