掌握多项式承诺 - KZG多项式承诺初学者指南

TLDR

KZG 承诺方案就像一个加密保险箱，用来安全地锁定多项式（数学方程），以便你可以在以后证明你拥有它们，而无需泄露其秘密。这就像是一个密封的承诺，你可以验证，而无需打开它并展示其内容。利用基于椭圆曲线的高级数学，它能够实现高效、可验证的承诺，是使区块链交易更私密和可扩展的关键部分。该方案对以太坊的升级尤其重要，可以快速安全地验证交易而不妥协隐私。

动机

ZKSNARKs

学习多项式承诺方案（PCS）很重要，因为它们在创建零知识简洁非交互式知识论证（ZKSNARKs）中发挥了关键作用。ZKSNARKs 是特殊的加密方法，允许一个人（证明者）向另一个人（验证者）展示他们知道一特定信息（如一个数字），而不透露该信息。这是通过将 PCS 和交互式 oracle 证明（IOP）结合使用来实现的。

现代 ZKSNARK = 功能承诺方案 + 兼容的交互式 oracle 证明 (IOP)

PCS 是一种证明你知道某个秘密函数（用多项式表示）的方法，而无需显示该函数本身。这就像承诺向某人展示一个秘密食谱，但你只向他们展示最终的菜肴，而不泄露食谱本身。这对于 ZKSNARKs 至关重要，因为它使证明者能够证明他们知道一个秘密函数，而不揭示其内容。

IOP 是另一种方法，帮助在不揭示秘密值的情况下证明你知道一个秘密值。它与 PCS 一起用于生成 ZKSNARK。IOP 帮助证明知识，而 PCS 使证明简短且易于检查。这种组合使得可以创建高效的 ZKSNARK，可用于许多领域，如区块链和隐私保留计算。

要生成 ZKSNARKs，你需要选择一个与 IOP 协同良好的 PCS。PCS 用于对多项式进行承诺并证明在某一点对多项式的评估而不透露多项式。IOP 用于创建知识证明，然后利用称为费亚-香农启发式的方法将其转化为非交互式证明。这使得能够生成和验证证明而不需要实时沟通，使 ZKSNARKs 在区块链和分布式系统中变得非常有用。

以太坊 Danksharding

KZG 承诺方案作为以太坊生态系统中的关键技术，尤其是在 Proto-Danksharding 及其预期演变为 Danksharding 的背景下。这种承诺方案是许多与零知识（ZK）相关的应用的基石，使得在不揭示底层信息的情况下有效且安全地验证数据。

基于以太坊的应用程序利用 KZG（Kate, Zaverucha 和 Goldberg）方案包括：

• Proto-Danksharding (EIP-4844)：该提案旨在降低在以太坊Layer1上发布数据的成本，以支持 rollups，采用 KZG 的多项式承诺方案。它引入了一种“承载数据的交易”类型，以容纳大量数据块，仅能从执行层访问对数据块的承诺。

• 数据可用性抽样：PCS 在以太坊路线图中启用了一项关键功能，即数据可用性抽样（DAS），允许验证者在不下载整个数据的情况下确认数据块的正确性和可用性。这种能力是借助 PCS 的独特特性，有效验证各种区块链应用程序，如以太坊的 Danksharding。

• PSE 的 Summa 清算证明协议：以太坊基金会的 PSE 组项目 Summa 在其清算证明协议中利用 KZG 承诺。这使得中心化交易所和保管机构能够证明其总资产超过其负债，同时保持用户余额信息的私密性。

• Scroll 的 zkRollups：Scroll 是以太坊的原生 zkEVM 二层，利用 KZG 生成对一组封装计算的多项式的承诺。这允许验证者请求在随机点的评估，以验证多项式表示的计算的准确性。

• Jellyfish：Jellyfish 在承诺阶段利用 KZG 承诺方案来生成对多项式的承诺。它利用 KZG 的同态特性，以高效的方式在不泄露其系数的情况下，在任意点评估多项式。

• Hyperplonk：Hyperplonk 利用多线性 KZG 承诺，表明其可应用于需要多线性多项式承诺的场景。

目标

现在我们已经有动力去学习 PCS，让我们开始定义我们的目标，即希望通过 KZG 方案解决的确切问题。

假设我们有一个函数或多项式 $f(x)$，定义为 $f(x) = f_0 + f_1x + f_2x^2 + \ldots + f_dx^t$。多项式 $f(x)$ 的次数是 $t$。

我们与 KZG 方案的主要目标是希望向某人证明我们知道这个多项式，而不透露该多项式，即多项式的系数。

在实际操作中，我们确切地做的是，我们证明我们知道这个多项式在某一点 $x=a$ 的特定评估。

我们写作 $f(a)$，对于某个 $x=a$。

在讨论 KZG 之前，你需要了解哪些内容

在我们进一步了解 KZG 方案之前，有一些重要的概念我们需要了解。幸运的是，我们可以通过足够的高中数学对 KZG 方案获得工程层面的理解。我们将努力获得对高级概念及其重要属性的直觉，而不必深入了解它们。这有助于我们在不被高级数学困扰的情况下看到 KZG 协议的流程。

我们需要知道：

模运算

analog_clock 插图展示了模运算，当小时数周期性地回归其限制时。在 KZG 中，仅需了解简单的算术—加法、减法、乘法和除法，以及模运算，就像钟表在 12 或 24 小时后复位。

我们通常用 mod $p$ 表示，以 perd p，表示对 $p$ 取模，其中 $p$ 是某个数字。

一阶有限域 $\mathbb F_p$

一阶有限域 $\mathbb F_p$，我们用 $\mathbb F_p$ 表示，这是一个特殊的数字集合，${1, 2, 3, \ldots, p-1}$，你可以对其进行所有常见的数学运算（加、减、乘和除，零除外），同时仍然遵循算术法则。

这个集合的“顺序”是它包含的元素数量，并且对于一阶有限域 $\mathbb F_p$，这个数字是一个质数。创建 $\mathbb F_p$ 的最常见方法是取所有大于或等于 0 的整数，然后通过 $p$ 进行划分，保留余数。这为我们提供了从 $0$ 到 $p-1$ 的数字集合，可用于算术运算。例如，如果 $p=5$，那么该集合将是 {0, 1, 2, 3, 4}，你可以以遵循算术法则的方式对这些数字进行加、减、乘和除。这集合是包含 5 个元素的有限域，我们表示为 $\mathbb F_5$，因为它恰好包含 5 个元素，并且这是一个质数。

在有限域 $\mathbb F_p$ 中进行模运算时，我们有良好的“包裹”特性，即该域表现得好像在达到 $(p - 1)$ 之后“包裹”了起来。

通常，当我们定义一个有限域时，我们定义该域的顺序 $p$ 和一项算术运算，如加法或乘法。如果是加法，我们将该域表示为 $(\mathbb F_p, +)$。如果是乘法，我们将其表示为 $(\mathbb F^_p, +)$。`` 告诉我们要排除零元素，以便我们能够满足有限域的所有必要属性，即主要是能够对数字进行除法并找到所有元素的逆。如果我们包含零元素，就无法找到零元素的逆。

在下一部分中，我们将了解如何通过群的生成器使 KZG 承诺方案能够作为一种高效、安全且可验证的多项式承诺方法，这使其成为加密协议的强大工具，尤其是在区块链技术中，这些属性至关重要。

群

群在概念上与有限域相似，尽管有一些小的变化。一个重要的区别在于，在群中，我们对集合只有一种算术运算，通常是加法或乘法，而不是有限域中的加法和乘法。类似于有限域，群的元素必须具有逆元素，并满足所有要求，下面的示例阐明了这一点。

我们用($\mathbb G, +)$ 来表示一个以加法为操作的群， ($\mathbb G^, .)$ 表示一个以乘法为操作的群；`` 告诉我们排除零元素以避免零除。

在下一部分中，我们使用一个示例来定义一个群。这将帮助发展我们在称一个数字集为群时的直觉。

群的生成器

生成器是在群内的一个元素，当与自身重复结合通过群的运算后，可以最终产生群内的其他所有元素。

从数学的角度看，如果你有一个群 ($\mathbb G, .)$ 和一个元素 $g \in \mathbb G$，我们称 $g$ 是生成器， если 所有的幂集合 $(g, g^2, g^3, ...)$ 等于有限群 $\mathbb G$，或者在无限群的情况下，通过这种重复操作覆盖 $\mathbb G$ 的所有元素。

此概念可以通过示例进行更好地解释。

我们将处理 ($\mathbb G_7, +)$ 的群元素 { ${0,1,2,3,4,5,6}$ } 和 ($\mathbb G^*_7, .)$ 的群元素 { ${1,2,3,4,5,6}$ }，采用模 $7$ 来寻找群的生成器。

加法群的生成器

我们的集合 ($\mathbb G_7, +)$ 拥有元素 { ${0,1,2,3,4,5,6}$ } 是一个群，因为它满足群的定义。

• 封闭性： 当你在集合中添加任何两个数字并在除以 $7$ 后取余时，你最终得到的结果仍然在集合内。
• 结合律： 对于集合中的任何数字 $a, b$ 和 $c$，$(a+b)+c$ 始终等于 $a+(b+c)$，即便在模 $7$ 下。
• 单位元素： 数字 $0$ 作为单位元素，因为当你将 $0$ 添加到集合中的任何数字时，你将得到同一个数字。
• 逆元素： 集合中的每个数字都有一个逆元素，使得当它们相加时，会回到单位元素 $0$。例如，$3$ 的逆元素是 $4$，因为 $3 + 4 = 7$，对 $7$ 取模 $7$ 后，即为 $0$。

现在，关于生成器。由于我们的群有质数阶 $7$，排除单位元素 $0$ 的任何元素都是生成器。我们以元素 $1$ 作为我们的生成器，即 $g = 1$。由于我们正处理加法群，在生成器 $g$ 下，我们的群元素将是 ${0, g, 2g, 3g, 4g, 5g, 6g}$。

从 $1$ 开始，通过模 $7$ 不断相加，我们得到：

• $1 + 1 = 2$（这就是模 $7$ 下的 $2*1$）
• $1 + 1 + 1 = 3$（这就是模 $7$ 下的 $3*1$）
• $1 + 1 + 1 + 1 = 4$（这就是模 $7$ 下的 $4*1$）
• $1 + 1 + 1 + 1 + 1 = 5$（这就是模 $7$ 下的 $5*1$）
• $1 + 1 + 1 + 1 + 1 + 1 = 6$（这就是模 $7$ 下的 $6*1$）
• $1 + 1 + 1 + 1 + 1 + 1 + 1 = 7$，（即模 $7$ 下的 $0$，即 $7*1$）

正如你所见，通过不断将 $1$ 相加模 $7$，我们可以生成该群中的其他每个元素。因此，$1$ 是群 ($\mathbb G_7, +)$ 的一个生成器。同样，我们可以选择 $2, 3, 4, 5, 6$ 中的任意数字作为我们的生成器，通过模 $7$ 进行重复添加，仍会生成整个群。这是质数阶群的一个特殊属性。

乘法群的生成器 对于模质数 $p$ 的整数乘法群，群 ($\mathbb G_p, .)$ 由整数 { ${1, 2, 3, \ldots, p-1}$ } 组成，其运算为模 $p$ 下的乘法。我们选择一个小质数来简化，例如 $p=7$。因此，我们的群 ($\mathbb G^_7, .)$ 在模 $7$ 下包含元素 { ${1, 2, 3, 4, 5, 6}$ }。请记住，由于排除了零元素，因此我们在标记中使用 ``。

这里是群的结构：

• 封闭性： 任何两个元素的乘积，经过模 $7$ 归约后，仍然是集合中的元素。
• 结合律： 对于集合中的任何数字 $a, b, c$，$(a \cdot b) \cdot c$ 始终等于 $a \cdot (b \cdot c)$，即使考虑模 $7$。
• 单位元素： 数字 $1$ 作为单位元素，因为当你用 $1$ 乘以集合中的任何数字时，会得到相同的数字。
• 逆元素： 集合中的每个数字都有一个乘法逆元素，使得它们相乘得出单位元素 $1$。例如，$3$ 的乘法逆是 $5$，因为 $3 \cdot 5 = 15$，对此取模 $7$ 后为 $1$。

让我们通过在模 $7$ 下不断乘以每个元素来验证每个元素是否确实是生成器：

• 开始以 $2$ 为例，不断乘以 $2$ 然后模 $7$：

  • $2^1 = 2$
  • $2^2 = 4$
  • $2^3 = 8 \equiv 1 \mod 7$
  • $2^4 = 16 \equiv 2 \mod 7$（在这里再次回到起点，显示 $2$ 不是生成器）

• 接下来试试 $3$：

  • $3^1 = 3$
  • $3^2 = 9 \equiv 2 \mod 7$
  • $3^3 = 27 \equiv 6 \mod 7$
  • $3^4 = 81 \equiv 4 \mod 7$
  • $3^5 = 243 \equiv 5 \mod 7$
  • $3^6 = 729 \equiv 1 \mod 7$（我们经历了所有元素后达到单位元素，因此 $3$ 是一个生成器）

你可以验证 $5$ 也是我们在模 $7$ 下的乘法群 ($\mathbb G^*_7, .)$ 的生成器。

为何在域运算中选择质数模

选择质数作为有限域运算的模数提供了多个优势并简化了域算术的各个方面：

1. 定义明确的除法： 在有限域中，每个非零元素必须具有乘法逆。如果模数是质数，集合 { ${1, 2, 3, \ldots, p-1}$ } 中的每个数字都具有模 $p$ 的乘法逆。这个特性允许在域内定义明确的除法运算，如果模数不是质数（除了特殊情况如 $p^n$ 的伽罗瓦域），则将无法实现。

2. 构造简单： 当模数为质数时，该域的构造比较简单。域的元素仅为整数集合 { ${1, 2, 3, \ldots, p-1}$ }，而进行模 $p$ 的场内操作相对直观。非质数模数构造域则要求更多的复杂结构，如多项式环。

3. 确保域属性： 使用质数模数可确保满足域属性。有限域是元素数量有限的集合。为了称该集合为域，必须满足包括加法和乘法单位元素的存在、每个元素均有加法和乘法逆，以及加法和乘法的交换、结合和分配定律的存在。质数模数确保所有这些属性都得以满足。

4. 非零元素的均匀分布： 在质数模数的有限域中，非零元素在乘法上均匀分布。这意味着，该域的乘法表没有“空缺”，并且每个元素在乘法表的每一行和列中仅出现一次（除了零元素的行和列）。

5. 使算法更简单化： 当涉及质数域时，数论和密码学中的许多算法变得更简单和高效。例如，使用扩展欧几里得算法可以高效的查找乘法逆，而对于非质数域则不再需要此类复杂的多项式运算。

6. 密码学安全性： 在密码学中，某些问题（如离散对数问题）的困难性在质数域中较为明确。这种困难性对加密系统的安全性至关重要。对于合成模数（尤其是未知因子的情况），其结构可能引入漏洞，或者使问题的困难性变得难以预测。

7. 优化计算： 一些质数（如 $31$ 或形式为 $2^n - 1$ 的质数）被 CPU 优化乘法运算，因此可以提供更快的计算时间，这在性能至关重要的应用中尤其有益。

在有限域运算中使用质数作为模数可以简化域算术，确保域属性得到满足，这对于理论和实际应用，尤其是在密码学中，是必不可少的。

加密假设

为了与 KZG 承诺方案协同工作，我们需要两个附加的假设。我们不会深入探讨这些假设为何必要，但我们会提供为什么这些加密假设对于 KZG 变得更安全的直觉。

离散对数

假设我们在群 $\mathbb G^*_p$ 中有一个生成元 $g$，而 $a$ 是有限域 $\mathbb F^_p$ 中的任何一个元素，$g^a$ 是群 $\mathbb G^\_p$ 中的某个元素。离散对数假设称，给定 $g$ 和 $g^a$，几乎不可能找到 $a$。这意味着我们不能轻易找到给我们这些元素的指数 $a$。

发展离散对数问题的直觉

想象你有一个特殊类型的锁，其工作与数字相关（我们称这个锁为“生成元”，命名为 $g$）。这个锁是一个魔法锁和钥匙集合的一部分，所有的东西都生活在一个名为 $\mathbb G^*_p$ 的魔术国度中。现在，你挑选一个秘密的数字 $a$ 并用其旋转你的锁 $g$ 若干次。结果，该锁停在一个新位置，让我们称之为 $g^a$。

如果有人走过并看到你的锁停在 $g^a$，即便他们知道它最初是 $g$，并知道其所属的魔法国度，弄清楚你转动了多少次（查找你的秘密数字 $a$）是极其困难的。

简单而言，离散对数问题告诉我们，尽管知道你拥有的数字是很简单的事情，但如果进行反向推理—看到结果并尝试猜测秘密数字—就像在一堆草垛中找镖箭一样。这种概念在密码学中至关重要，确保某些秘密极难揭示。

强的 Diffie-Hellman

假设我们在群 $\mathbb G^*_p$ 中有一个生成元 $g$，而 $a, b$ 是任意元素有限域 $\mathbb F^_p$ 中的任何元素，$g^a, g^b$ 是群 $\mathbb G^\_p$ 中的某些元素。强的 Diffie-Hellman 假设表明，$g^a$ 和 $g^b$ 是无法区分的，等同于 $g^{ab}$。这意味着我们无法从 $g^a$ 和 $g^b$ 中提取掉关于 $g^{ab}$ 的额外信息。

发展强的 Diffie-Hellman 直觉

想象你正身处于一个以其魔法饼干而闻名的世界，并且有一种神秘成分（我们的“生成元”，$g$）使它们特别。两个大师级的面包师，一个名叫 Alice 另一个叫 Bob，各有自己独特的使用这种成分的技巧，分别用其秘密食谱 $a$ 和 $b$ 表示。

当 Alice 使用她的秘密食谱来烘焙饼干时，她制作了一批特别的 $g^a$。Bob 也用他的食谱制作了一批特殊的 $g^b$。

现在，假设 Alice 和 Bob 决定合作，将他们的秘密食谱结合在一起，创造一个超秘密的饼干批次 $g^{ab}$。强的 Diffie-Hellman 假设表示即便有谁尝过 Alice 和 Bob 两者的批次，他们还是无法推测出结合的超秘密批次的味道。结合食谱的风味与任何其他批次几乎无法区分。

因此，总之，强的 Diffie-Hellman 假设告诉我们，仅仅知道各自的秘密（食谱）的结果并没有帮助任何人揭示组合之后的结果。这是安全通信的基石，确保即便有他人知道分开的部分，但组合的秘密依旧保持安全和不可推测。

配对函数

假设我们在群 $\mathbb G^*_p$ 中有一个生成元 $g$，而 $a, b$ 是任意元素有限域 $\mathbb F^_p$ 中的任何元素， $g^a$ 和 $g^b$ 是组 $\mathbb G^\_p$ 中的某些元素。

配对函数是一个数学函数，接受两个输入并通过将不同输入对映射到一个独特值来生成一个输出。它有两个重要属性：线性性和非退化性。

• 线性性意味我们可以在一个可逆的方式中移动。
• 非退化性 contends 像，如果我们将配对函数应用到相同的元素，结果不会是群的单位元素。

让我们对这些属性做一些更严谨的定义。

一个配对函数 $e:$ $\mathbb G_1 \times \mathbb G_2 \rightarrow \mathbb G_T$，该函数满足，

线性属性：$e(g^a, g^b) = e(g, g^{ab}) = e(g^{ab}, g) = e(g,g)^{ab}$

非退化属性：$e(g,g) \neq 1$，意即输出不是单位元素。

当 $\mathbb G_1$ 和 $\mathbb G_2$ 为同一群时，我们称之为对称配对函数；否则，它就是不对称配对函数。

这里有一些很好的资源，从实际角度了解配对函数^3^9。

发展配对函数的直觉

想象有两个独立的岛屿，各自栖息着独特的魔法生物。第一座岛上生活着独角兽，每种独角兽都有其独特的颜色，而第二岛则栖息着龙类，每种龙都有其独特的火焰颜色。配对函数就像一座魔法桥，将独角兽与龙相连，创造一种独特的新魔法生物，名为 Dracorn，同时具备两者的特征。

以下是你如何思考这个配对函数，而不必被轮廓性的细节困扰：

• 两个群体： 认为独角兽和龙分别属于两个不同的群体（在数学术语中，通常称为 $\mathbb G_1$ 和 $\mathbb G_2$）。
• 配对函数： 魔法桥是影响配对功能的桥。当一只独角兽与一条龙在这座桥上相遇时，配对函数将它们结合成一个多角兽。这个多角兽有着特殊的光芒，独特地对应于特定的独角兽与龙的组合（具备可逆性）。
• 独特结果： 就像每对独角兽和龙都会产生一个特有的光环一样，在数学上，配对函会从每个群体中取一个元素并产生一个独特的输出。

这为何神奇？ 因为尽管有无数可能的独角兽与龙组合，但每种组合（配对）都产生一种独特的 Dracorn。这在密码学中至关重要，因为它允许实现复杂操作，这些操作支撑许多安全协议，确保每个组合都是独特且可追溯至原始组合。

简而言之， 想象你有两组钥匙（独角兽和龙），当你组合每个组中的一个钥匙时，就会获得独特的锁（Dracorn）。其魔力在于这种组合是可预测且安全的，允许安全的交互，依赖于这些独特结果的确定性，而不泄露原始钥匙。

配对函数使得先进的加密技术成为可能，例如那些用于某些类型的数字签名和加密，从而实现这种“跨群体”的安全交互。

承诺的性质

承诺方案就像数字世界中的秘密魔法师。它们允许某人对某个信息（我们称之为秘密消息）做出承诺，以一种将其与承诺绑定的方式，而不让其他人知道秘密的内容。其工作原理如下：

• 做出承诺（承诺）： 你选择一个秘密消息并使用一种特殊的魔法（承诺方案）生成一个魔法印章（承诺）。这个印章证明你拥有一个秘密，但将其隐藏起来。
• 保守秘密（隐藏性）： 尽管你已做出此印章，但其他人无法看到你的秘密信息。就像你将其锁在一个箱子里，并且只有你有钥匙。
• 证明诚信（绑定性）： 此承诺的魔力在于，你无法在不打破印章的情况下后来更改你的秘密消息。这意味着，一旦你做出承诺，你就被约束于此。

随后，当时机成熟要揭示你的秘密时，你可以展示原始消息并证明其与你之前制作的印章一致，从而允许其他人（验证者）检查并确认你的秘密消息确实是最初你承诺的内容，表明你保持了承诺。

绑定和隐藏的性质非常重要，它们与我们在离散对数和强的 Diffie-Hellman 假设所做的上述加密假设密切相关。

不过现在，我们不需要深入探讨技术细节。如果你想了解更多，这里有来自 Dan Boneh 教授的有关 PCS 的精彩资源^4。

通过这些背景知识，我们准备好解释 KZG 协议的流程并理解其构建原理。

KZG 协议流程

让我们重申一下，我们希望通过 KZG 协议解决的问题。

我们要证明我们知道一个函数或多项式在某点$x=a$的特定评估，而不揭示它。

在 KZG 承诺方案中，受信第三方、证明者和验证者的角色对其功能和安全至关重要。以下是每方在该过程中的贡献：

1. 受信第三方（设置机构）： 该实体负责 KZG 方案的初始设置阶段。它们生成将用于承诺和证明的公共参数（PP）或公共引用字符串（CRS），基于只有它们知道的一个秘密。这个秘密对于承诺的构建至关重要，但在设置结束后必须丢弃（或保持极端安全），以确保系统的完整性。人们对该方的信任是至关重要的，因为如果秘密被处理不当或泄露，可能会危及整个系统。该方的角色在它们生成公共引用字符串（CRS）并将其分发给证明者和验证者后便终止。此后，它们不参与协议的进一步步骤，无论是证明还是验证。

2. 证明者： 证明者是希望承诺特定数据（如多项式）而不揭示其内容的一方。使用受信第三方提供的 CRS，证明者计算其数据的承诺。当需要证明其数据某些属性时（如在特定点的多项式评估），证明者可以根据承诺生成证明。该证明表明其数据具有某些属性而不泄露数据本身。

3. 验证者： 验证者是对证明者关于其秘密数据的主张感兴趣的一方。验证者使用证明者提供的证明以及来自受信第三方的 CRS 验证证明者关于其数据的主张是否正确。这是在验证者永远不会直接访问秘密数据的情况下完成的。 KZG 方案的优势确保，如果证明验证正确，验证者可以相当有信心证明者的主张是成立的，前提是受信第三方正确地执行任务且秘密未被泄露。

三方之间的这种交互使得在各种加密应用中，尤其是区块链协议和安全计算中，能够实现安全且高效的数据属性验证，提供了透明度与隐私之间的平衡。

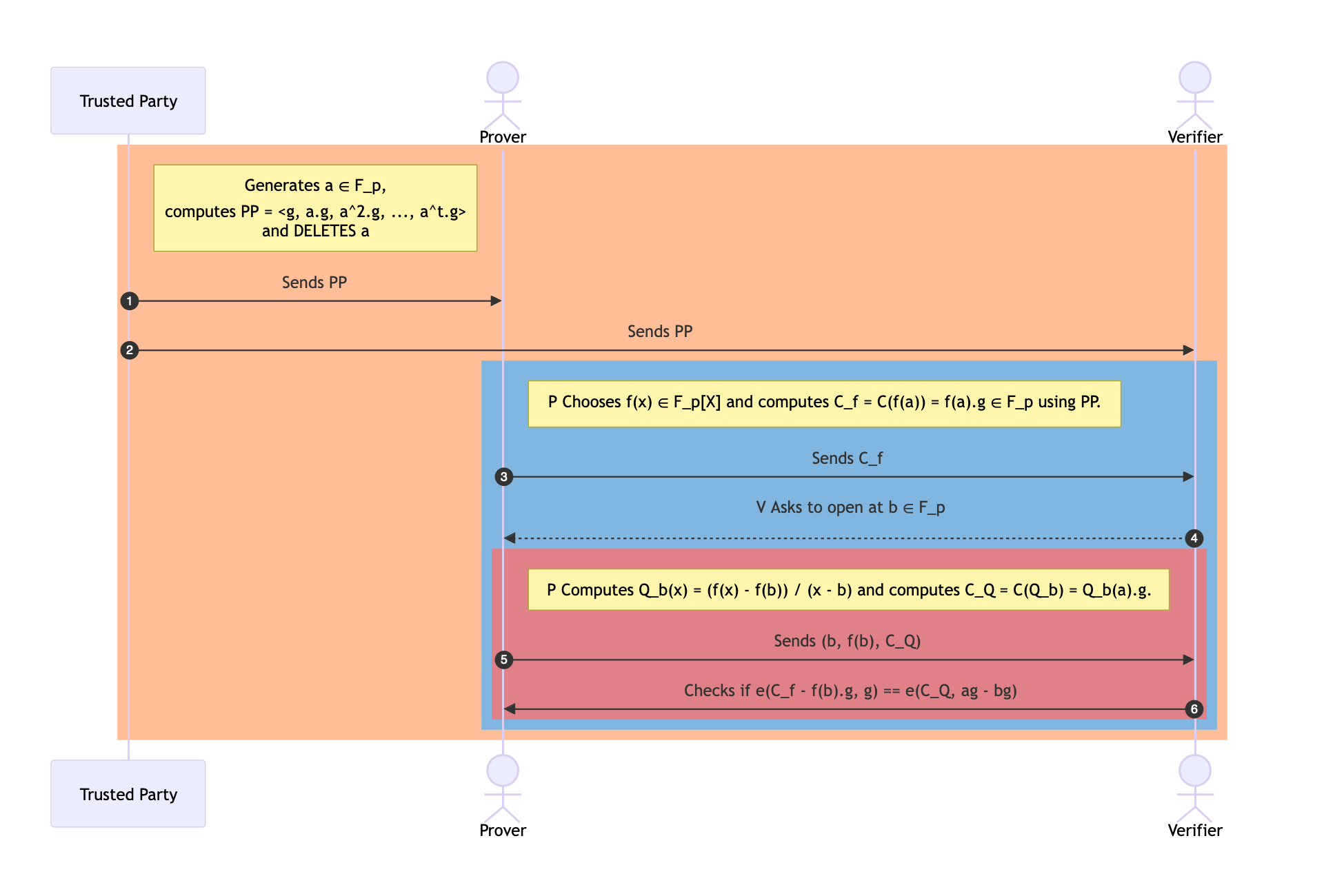
下面是详细的序列图，说明典型 KZG 协议中的流动。

sequenceDiagram
    autonumber
    participant TP as 受信第三方
    Actor P as 证明者 
    Actor V as 验证者

    rect rgb(255, 190, 152)
    note right of TP: 生成 a ∈ F_p， <br /> 计算 PP = <g, a.g, a^2.g, ..., a^t.g> <br /> 并删除 a 
    TP->>P: 发送 PP
    TP->>V: 发送 PP
    rect rgb(128,182,223)
    note right of P: P 选择 f(x) ∈ F_p[X] 并使用 PP 计算 C_f = C(f(a)) = f(a).g ∈ F_p。
    P->>V: 发送 C_f
    V-->>P: V 请求在 b ∈ F_p 处打开。
    rect rgb(224,128,135)
    note right of P: P 计算 Q_b(x) = (f(x) - f(b)) / (x - b) 并计算 C_Q = C(Q_b) = Q_b(a).g。
    P->>V: 发送 (b, f(b), C_Q)
    V->>P: 检查 e(C_f - f(b).g, g) == e(C_Q, ag - bg)
    end
    end
    end

受信设置

受信第三方选择一个随机元素 $a \in \mathbb{F}_p$。然后，它们计算公共参数（PP）或公共引用字符串（CRS），形式为 < $g, {a^1}.g, {a^2}.g, \ldots, {a^t}.g$ >。然后，它们删除 $a$。该步骤的删除 $a$ 对于确保系统的安全性极为重要。

接着，受信方将 CRS 发送给证明者和验证者。

在实践中，这一过程是通过多方计算 (MPC) 封装的，秘密以如此方式生成，即只要至少有一个参与者保持诚实，该秘密的随机性就能得到保障。

受信设置是一个一次性程序，生成该加密协议运作所需的数据。此数据必须在每次运行协议时使用，

但一旦生成且秘密被遗忘后，创建仪式的人员就无需进一步参与。该设置的信任基础在于，生成数据所用的秘密在设置后被安全丢弃，确保数据在未来的使用中保持安全。

现代协议常使用 powers-of-tau 设置，涉及数千个参与者。最终输出的安全性依赖于至少一个未公布其秘密的参与者的诚实。这一方法在实践中被认为“足够接近于无信任”，使其成为需要受信设置的密码协议的实用解决方案。

以太坊详细说明了受信设置仪式，欲了解更多请参考^2。

初始配置

假设证明者有一个在有限域 $\mathbb F_p$ 中定义的函数或多项式 $f(x)$，形式为 $f(x) = f_0 + f_1x + f_2x^2 + \ldots + f_dx^t$。多项式 $f(x)$ 的次数为 $t$，小于有限域 $\mathbb F_p$ 的阶数 $p$。

我们通常将其表示为 $f(x) \in \mathbb{F}_p[x]$。

$\mathbb{G}_p$ 是一个阶数为 $p$ 的椭圆曲线群，具有生成元 $g$。

通常，选择的质数阶 $p$ 为 $p > 2^k$，其中 $k$ 为某个安全参数。实际上，质数 $p$ 是非常大的。

证明者还选择一个满足双线性和非退化属性的配对函数。配对的表示如下：

$e:$ $\mathbb G_1 \times \mathbb G_2 \rightarrow \mathbb G_T$

为了简化此步骤，证明者选择一个多项式 $f(x) \in \mathbb{F}_p[x]$，其中 $f(x)$ 的次数最多为 $t$，小于有限域 $\mathbb{F}_p$ 的阶数。证明者同时选择一个配对函数 $e$，在椭圆曲线群 $\mathbb{G}_p$ 上。

多项式的承诺

设多项式 $f(x)$ 的承诺表示为 $C_f$。承诺就像哈希函数。

因此，$C_f = {f(a)} \cdot g = {(f_0 + f_1a + f_2a^2 + \ldots + f_ta^t)} \cdot g$。此处 $f(a)$ 是在 $x=a$ 处的多项式评估结果。

尽管证明者不知道 $a$，他或她依然可以在 $x=a$ 处计算多项式的承诺。

因此我们有，$C_f = {f(a)} \cdot g = {(f_0 + f_1a + f_2a^2 + \ldots + f_ta^t)} \cdot g$。

$C_f = {f_0} \cdot g + {f_1a} \cdot g + {f_2a^2} \cdot g + \ldots + {f_ta^t} \cdot g $。

$C_f = {f_0} \cdot g + {f_1} \cdot (ag) + {f_2} \cdot ({a^2}g) + \ldots + {f_t} \cdot ({a^t}g)$。

从 CRS 中，证明者 знает这些值 < $g, {a^1}.g, {a^2}.g, \ldots, {a^t}.g$ >，他或她可以计算这个值作为多项式的承诺 $C_f$，然后发送给验证者。

多项式的打开

在收到来自证明者的多项式承诺 $C_f$ 后，验证者在协议中采取下一步，选择一个来自有限域 $\mathbb F_p$ 的随机点，我们将其称为 $b$。然后，验证者要求证明者打开或揭示该多项式在此特定点的值。

“打开多项式”是什么意思？ 在 $x=b$ 的多项式打开涉及在该点计算多项式的值，数理上表示为 $f(b)$。这是通过使用所选点 $b$ 来评估该多项式来完成的：

$f(b) = f_0 + f_1b + f_2b^2 + \ldots + f_tb^t$。让我们假设该计算的结果为$f(b) = d$。证明者现在的任务是向验证者提供一个评估证明，这证据证明$f(b)$确实等于$d$。

让我们一步一步来拆解。

计算评估证明：
证明者确定商多项式，我们将其称为$Q(x)$，并计算其承诺。这一步对于创建可验证的证明至关重要。由于我们知道$f(b) = d$，多项式$(f(x)−d)$将在$x=b$处具有一个根，这意味着$(f(x)−d)$可以被$x−b$整除，没有余数——这是Little Bezout定理的结果^1。

用数学术语表达，商多项式为： $Q(x) = \frac{f(x) - f(b)}{x - b} = \frac{f(x) - d}{x - b}$

商多项式$Q(x)$的承诺用$C_Q$表示。使用在可信设定中提供的公共参考字符串（CRS），证明者计算$C_Q$： $C_Q = {Q(a)} \cdot g$。

只要$(f(x) - f(b))$可以被$(x−b)$整除，证明者就能够计算$C_Q$。如果不是这样，则$Q(x)$就不是一个适当的多项式，即商多项式将有一个分母和一些负指数，证明者将无法仅仅使用CRS计算评估证明$C_Q$。

最后，证明者向验证者发送元组< $b, f(b), C_Q$ >，完成协议的此步骤。

验证证明

首先让我们总结一下验证者在协议中目前掌握了哪些数据。

掌握的数据：验证者知道：

• 多项式的承诺$C_f$。
• 开放点$b$。
• 多项式在$b$处的值，记为$f(b)$。
• $b$处的商多项式的承诺，记为$C_Q = {Q(a)} \cdot g$。

承诺方案的性质：

• 完整性： 如果任何事情是真的，那么一个承诺方案是完整的。
• 健壮性： 如果任何可证明的事情都是真的，即错误的事情不能通过该方案证明，那么称其为健壮的。

商多项式和验证：

回想一下商多项式为： $Q(x) = \frac{f(x) - f(b)}{x - b} = \frac{f(x) - d}{x - b}$。

因此，$(x - b) \cdot Q(x) = f(x) - d$

在$x=a$处评估，我们得到： $(a - b) \cdot Q(a) = f(a) - d$

两边乘以生成元$g$，我们得到：

$(a−b) \cdot Q(a) \cdot g = f(a) \cdot g − d \cdot g$

现在，验证者知道$C_Q = Q(a) \cdot g$和$C_f = f(a) \cdot g$。

替换后，我们得到：

$(a−b) \cdot C_Q = C_f − d \cdot g$

如果验证者可以确认上述等式的有效性，则表示承诺已通过验证。然而，由于验证者不知道$a$的值，他们无法直接验证该等式的真实性。

但是，验证者可以使用上面概述的椭圆曲线配对来验证即使不知道$a$的等式约束。请记住，配对函数被表示为：

$e:$ $\mathbb G_1 \times \mathbb G_2 \rightarrow \mathbb G_T$ 满足以下条件，

双线性特性：$e(g^a, g^b) = e(g, g^{ab}) = e(g^{ab}, g) = e(g,g)^{ab}$

非退化特性：$e(g,g) \neq 1$，意味着输出不是单位元素。

现在我们暂时使用一个对称配对函数$e:$ $\mathbb G \times \mathbb G \rightarrow \mathbb G_T$。

证明者必须检查等式$(a−b) \cdot C_Q = C_f − d \cdot g$。

配对函数从群$\mathbb G$中的任何两个元素映射到$\mathbb G_T$中的一个元素。

• 像$C_f$或$C_Q$这样的承诺是通过将一个数字（标量）乘以群的生成元$g$而得到的。
• 由于$C_f$和$C_Q$都是此操作的结果，因此它们属于群$\mathbb G$。
• 当我们将$C_Q$乘以两个数字$a$和$b$的差作为标量时，结果$(a−b) \cdot C_Q$保持在群$\mathbb G$中。
• 同样，$C_f$是一个群元素，$d \cdot g$也是如此，因为它是生成元乘以一个标量。
• 从$C_f$中减去$d \cdot g$给我们另一个在群中的元素$C_f − d \cdot g$。
• 所有这些结果元素 جزء 都是$\mathbb G$的一部分，并可以在配对函数中使用。

因此，在两边应用配对函数，使用生成元$g$作为第二个参数，等式约束变为：

$e((a−b) \cdot C_Q, g) = e(C_f − d \cdot g, g)$

我们仍然无法计算$a-b$，因为没有人知道$a$。但我们可以利用配对函数的双线性特性：

$e(g^a, g^b) = e(g, g^{ab}) = e(g^{ab}, g) = e(g,g)^{ab}$

我们可以将等式约束重写为：

$e(C_Q, (a−b) \cdot g) = e(C_f − d \cdot g, g)$

$e(C_Q, a \cdot g − b \cdot g) = e(C_f − d \cdot g, g)$

尽管验证者不知道$a$，但他或她可以从公共参考字符串中知道$a \cdot g$。因此，验证者现在可以检查上述等式是否成立。这结束了对评估证明的验证。

多项式的完全开启与部分开启

• 完全开启过程：

  • 证明者向验证者发送完整的多项式。
  • 使用CRS，验证者独立计算多项式的承诺。
  • 验证者然后检查独立计算的承诺是否与证明者最初发送的承诺匹配。

• KZG中的部分开启过程：

  • 证明者可以选择部分开启，而不是开启整个多项式。
  • 这意味着证明者在一个特定点上揭示多项式的值。
  • 这种部分揭示称为评估证明。

KZG手动演示

现在，让我们通过一个小的有限域手动推导KZG协议的步骤。我们可以手动计算所有有限域运算和配对运算，以感受KZG协议的流程和验证多项式承诺。

KZG手动演示 - 初始配置

• 我们将使用有限域$(\mathbb F_{11}, + )$。因此，素数$p = 11$。这意味着所有有限域运算都将在模11下进行。
• 有限域集合是{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}。
• 生成元$g = 2$在$(\mathbb G_{11}, +)$中。
• 这意味着群运算使用加法，模11。
• 证明者选择多项式$f(x) = 3x^2 + 5x + 7$。
• 因此，多项式$f(x)$的度为$t = 2$。
• 配对函数为$e(x, y) = xy$，在$(\mathbb G_{11}, +)$上。

KZG手动演示 - 可信设定

• 可信方随机选择一个秘密数字。假设$ a = 3 $是秘密数字。
• 他们生成公共参数或公共参考字符串（CRS）< $g, {a^1}.g, {a^2}.g, \ldots, {a^t}.g$ >。
• 这个值等于< $2, 3 \cdot 2, {3^2} \cdot 2$ >，经过模11运算后结果为< $2, 6, 7$ >。
• 可信方删除秘密数字$a$。
• 可信方将CRS发送给证明者和验证者。

KZG手动演示 - 多项式的承诺

• 证明者计算多项式的承诺$C_f$。
• $C_f = f(a) \cdot g = {f_0} \cdot g + {f_1} \cdot (ag) + {f_2} \cdot ({a^2}g) $。
• $C_f = 7 \cdot g + 5 \cdot (ag) + 3 \cdot a^2g = 7.2 + 5.6 + 3.7 = 65 = 10$ (mod 11)。
• 证明者将多项式的承诺$C_f = 10$发送给验证者。

KZG手动演示 - 多项式的开启

• 验证者要求证明者在$x = 1$处打开多项式。
• 证明者计算商多项式$Q(x) = \frac{f(x) - f(1)}{x - 1} = \frac{f(x) - d}{x - b}$。
• 计算$f(1) = d = 3.1^2 + 5.1 + 7 = 4$ (mod $11$)。
• $Q(x) = \frac{3x^2 + 5x + 7 - 4}{x - 1} = \frac{3x^2 + 5x + 3}{x - 1}$。
• 除以首项：$3x^2$除以$x$得到$3x$。我们在除法条上写下$3x$。
• 将除数乘以商的首项：将$x - 1$乘以$3x$得到$3x^2 - 3x$。
• 从多项式中减去：从$3x^2 + 5x$中减去$3x^2 - 3x$得到$8x$。
• 除下一个项：将$+3$带下，得到$8x + 3$。
• 除以下一个项：$8x$除以$x$得到$8$。在$3x$旁边写下$+8$。
• 再次乘法：将$x - 1$乘以$8$得到$8x - 8$。
• 再次减去：从$8x + 3$中减去$8x - 8$得到$11$。
• 应用模$11$：我们对每一项进行模$11$运算。由于$11$在模$11$下为$0$，余数为$0$。
• 证明者计算$C_Q$的承诺$C_Q = Q(a) \cdot g = 3 \cdot ag + 8 \cdot g = 3.6 + 8.2 = 34 = 1$ (mod 11)。
• 证明者发送给验证者< $1, f(1), C_Q$ > = < $1, 4, 1$ >。

KZG手动演示 - 验证

• 验证者必须检查配对约束$e(C_Q, a \cdot g − b \cdot g) = e(C_f − d \cdot g, g)$。
• 左边（L.H.S）：$e(1, 6 - 1.2) = e(1, 4) = 1.4 = 4$ (mod 11)。
• 右边（R.H.S）：$e(10 - 4.2, 2) = e(2, 2) = 2.2 = 4$ (mod 11)。
• 这证明了等式约束为真，因此验证了评估证明。

KZG的安全性 - 删除毒性废物

• 想象一下证明者不小心找到了秘密数字$a$，或者可信方向恶意证明者泄露了$a$。
• 证明者在$x=3$计算$f_1(x) = 3x^2 + 5x + 7$。我们得到$f_1(2) = 3.3^2 + 5.3 + 7 = 49 = 5$ (mod 11)。
• 证明者在$x=3$计算$f_2(x) = 2x^2 + 7x + 10$。我们得到$f_2(2) = 2.3^2 + 7.3 + 10 = 49 = 5$ (mod 11)。
• 这破坏了承诺机制的绑定特性，导致恶意证明者伪造证明。
• 因此，可信方在生成CRS后删除秘密数字$a$非常重要。

KZG使用非对称配对函数

一个非对称配对函数表示为：

$e:$ $\mathbb G_1 \times \mathbb G_2 \rightarrow \mathbb G_T$。

设$\mathbb G_1$的生成元为$g_1$，$\mathbb G_2$的生成元为$g_2$。

证明者必须检查等式$(a−b) \cdot Q(a) = f(a) − d$。

两边乘以$g_1$，我们得到：

$(a−b) \cdot Q(a) \cdot g_1 = f(a) \cdot g_1 − d \cdot g_1$

$(a−b) \cdot C_Q = C_f − d \cdot g_1$

在两边应用非对称配对函数，我们得到：

$e((a−b) \cdot C_Q, g_2) = e(C_f − d \cdot g_1, g_2)$

使用双线性特性，我们得到：

$e(C_Q, (a−b) \cdot g_2) = e(C_f − d \cdot g_1, g_2)$

$e(C_Q, a \cdot g_2 − b \cdot g_2 ) = e(C_f − d \cdot g_1, g_2)$

这里的$a \cdot g_2$将是$\mathbb G_2$的CRS的一部分，而其他的一切可以由计算或是$\mathbb G_1$的CRS部分产生。

不动的紧凑性

KZG多项式承诺方案确保无论多项式的长度如何，承诺和评估证明的大小都是固定的，提供了一致和空间高效的加密操作^5^7。

KZG多项式承诺方案的一个关键好处是其高效的空间使用。不管我们所处理的多项式的长度或复杂性如何，该多项式的承诺——本质上是其加密“ footprint ”——始终是一个在数学群$\mathbb G$中固定大小的元素。这意味着随着多项式度数的增加，承诺的大小不会增加。此原则同样适用于评估证明，这是我们提供的证据，以证明我们的承诺是准确的。无论我们是在一次验证一个值还是多次（批处理模式），证明的大小始终是一致的。这种大小上的一致性转化为可预测和高效的存储需求，对于加密实践中的应用是一个重要特性。

KZG批处理模式

KZG承诺也可以在多个点上或使用多个多项式或其组合进行开启和验证。这在实践中称为批处理模式。

批处理模式单个多项式，多点

在批处理模式中，验证者要求证明者验证一组点$B =$ { $b_1, b_2, b_3, \ldots, b_n$ }，其中$n < t$，$t$为多项式$f(x)$的度。对于这些点，证明者计算值$f(b_1) = d_1, f(b_2) = d_2, \ldots, f(b_n) = d_n$并形成集合$D =$ { $d_1, d_2, d_3, \ldots, d_n$ }。

然后，证明者创建一个多项式$P(x) = (x - b_1)(x - b_2)\ldots(x - b_n)$。由于$n < t$，可以将$f(x)$除以$P(x)$，得到$f(x) = P(x)Q(x) + R(x)$，其中$Q(x)$是商多项式，$R(x)$是余数。这个除法暗示了$f(x)$可以如此表示，而并不意味着$f(x)$直接被$Q(x)$整除。

商多项式$Q(x)$的承诺，记为$C_Q$，连同集合$B$，由证明者发送给验证者。可选择性地，证明者也可以将余数多项式$R(x)$发送给验证者。尽管如此，验证者具备独立计算$R(x)$的能力，考虑到对每个$ b_i $在$ B $中，$ P(x) $评估为零，这会导致$ f(x) = R(x) $对$ B $中的所有$ b_i $成立。

由于$ Q(x) $的次数为$n$，而$R(x)$的次数小于$n$，因此，验证者知道$R(x)$在$n$个点的评估值，可以通过拉格朗日插值来确定$R(x)$^10。

验证者还计算多项式$P(x)$和$R(x)$，以及它们的承诺$C_P = P(a) \cdot g$和$C_R = R(a) \cdot g$。他们继续通过确保$ f(b_i) = R(b_i) $对$ B $中的所有$ b_i $成立，并且在$x = a$处等式$ f(x) = P(x)Q(x) + R(x) $成立以验证批量评估。

验证者需要评估上述约束以验证证明。然而，由于$x = a$的秘密开启未知，因此他们无法直接评估。但是，就像以前一样，验证者可以通过配对解决这个问题。

要进行验证，验证者检查：

• $f(b_i) = R(b_i)$对于$B$中的每个$b_i$，将提供的$D$值与它们在每个$b_i$处对$R(x)$的计算结果进行比较。

• 等式$ f(x) \cdot g - R(x) \cdot g = P(x)Q(x) \cdot g $在$x = a$处被评估，简化为$ C_f - C_R = P(a) \cdot C_Q $，使用已知的承诺和秘密$a$。

尽管不知道$a$，验证者利用配对对证明进行评估：

• 由于$ C_f $和$ C_R $均属于$\mathbb G$，它们的差也一样。
• 鉴于$ C_Q $属于$\mathbb G$且$ P(a) $作为标量，$ P(a) \cdot C_Q $仍然在$\mathbb G$中。

应用配对函数得到：

$e(C_f − C_R, g) = e(P(a) \cdot C_Q, g)$

根据双线性特性，我们得到：

$e(C_f - C_R, g) = e(C_Q, C_P)$

其中$C_P = P(a) \cdot g$。鉴于此，验证者可以确认等式的真实性，从而验证证明。

参考文献

• 原文链接： github.com/thogiti/thogi...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～