针对全同态加密的新型密钥恢复攻击

全面同态加密（FHE）是一个快速发展的领域，能够实现一些有趣的隐私保护应用。这些方案允许在加密数据上执行任何计算，而不透露数据本身的信息，同时在解密时能产生准确的计算结果。

最近，关于FHE的安全定义发表了两篇论文。这些论文表明，通过在合理假设下稍微增强攻击者的能力，可以构造出切实可行的密钥恢复攻击。这些攻击适用于各种已建立的库，例如SEAL、OpenFHE、Lattigo、TFHE-rs和TFHELib。

在这篇文章中，我们将首先总结有噪声学习（Learning With Error, LWE）问题，以理解这些攻击的基础。为阐明本文概念，提供了一个玩具实现。然后，我们将简要介绍适用于FHE的一般特性和安全模型。文中将介绍新的攻击及其对知名实现的实际结果。最后，我们将讨论这些论文如何帮助理解FHE方案的安全性和潜在的陷阱。

有噪声学习

如今，大多数FHE方案都是基于有噪声学习↗（LWE）问题或其变体。除了FHE外，LWE在密码学中也具有重要性，并用于构建一些后量子签名算法。为了理解后续的攻击，首先我们需要介绍LWE的一些特性。

在LWE加密系统中，秘密密钥 ( s=(s0,…,s{n-1}) \in \mathbb{Z}_q^n ) 是一个随机生成的向量，其中 ( q \geq 2 ) 是正整数，( n \geq 1 ) 是大小参数。为方便起见，我们假设消息 ( m \in {0,1} ) 为单比特。消息的加密 ( c=(a,b) ) 由以下公式给出：

[ b = \langle a,s \rangle + \lfloor \frac{q}{2} \rfloor m + e ]

其中 ( a \in \mathbb{Z}_q^n ) 随机生成，( e \in \mathbb{Z}_q ) 为一个随机生成的小噪声。运算符 ( \langle , \rangle ) 是标准内积。密文 ( c=(a,b) ) 解密的方式为：

[ m = \lceil \frac{2}{q} (\langle a,s \rangle - b) \rceil \mod 2 ]

其中 ( \lceil \cdot \rceil ) 是取整函数。由于加密是线性的，容易看出LWE具有同态加密特性。实际上，将两个密文 ( (a_1,b_1) ) 和 ( (a_2,b_2) ) 相加得到以下结果：

[ (a_1+a_2,b_1+b_2) = \left(a_1+a_2, \langle a_1,s \rangle + \langle a_2,s \rangle + \lfloor \frac{q}{2} \rfloor (m_1+m_2) + e_1 + e_2\right) = \left(a_1+a_2, \langle a_1 + a_2 ,s \rangle + \lfloor \frac{q}{2} \rfloor (m_1 + m_2) + e_1 + e_2\right) ]

这种新密文在解密时的结果为 ( m_1 + m_2 \mod 2 )。需要注意的是，这个新密文的噪声为 ( e = e_1 + e_2 )。

我们在Sage中创建了一个玩具示例，能够可视化实践中的工作原理：

sage: from lwe_binary import LWE
sage: lwe = LWE()
sage: s = lwe.keygen()
sage: c1 = lwe.encrypt(1,s)
sage: c1
((19331, 40593, 16415, 19987, 16358, 18642, 47726, 28920, 19322, 60414, 12111, 17241, 18520, 8379, 53280, 10978, 19388, 16743, 45284, 21682, 47339, 39674, 8962, 54166, 47172, 45000, 63534, 34439, 64653, 55681, 4290, 9750, 26215, 7889, 63029, 48475, 24295, 16684, 985, 30639, 61753, 46423, 18752, 33102, 50675, 30985, 23307, 42284, 46957, 19790, 59442, 60157, 59752, 23379, 16232, 12181, 15445, 807, 23396, 50120, 3860, 4103, 40049, 60981),
 96783)
sage: c2 = lwe.encrypt(1,s)
sage: c2
((13517, 22342, 34502, 10213, 59358, 36523, 19179, 41645, 54456, 24418, 52899, 60503, 39366, 8134, 40786, 44523, 9776, 26754, 28382, 24096, 43228, 35122, 41908, 7829, 31890, 45217, 28184, 34849, 53646, 53793, 8464, 4813, 52526, 39710, 20416, 31007, 20280, 47836, 34965, 15035, 48543, 36918, 20897, 21437, 20349, 48825, 5235, 20126, 43955, 15241, 15094, 63494, 15495, 25602, 37324, 5314, 55223, 41252, 54368, 28510, 39219, 9133, 7663, 15206),
 60423)
sage: c = lwe.enc_add(c1, c2)
sage: lwe.decrypt(c, s)
0

在这里，我们对值1进行两次加密，然后执行同态加法，最后解密结果。我们验证了LWE的加性同态特性，因为 ( 1 + 1 = 0 \mod 2 )，而仅处理加密数据。前面的实现使用了非常小的参数用于实验，但不应用于敏感应用。

我们已经看到LWE具有加性同态加密特性，或可视为XOR门。大多数当前FHE构造基于LWE。然而，从LWE构建一种全面同态加密同样需要具备乘法同态特性，即AND门。为LWE建造AND门更具挑战性且针对每种方案构造具体，我们在此不作详述。关于更多细节，Zama的深度报道文章↗是非常好的资料。

全同态加密

在这一部分，我们将从更高层次解释满足FHE的属性。这些属性是FHE方案特有的，使得安全定义更难验证，正如我们将看到的那样。

基本上，一个FHE方案是由加密和解密算法 ( \mathrm{Enc} ) 和 ( \mathrm{Dec} ) 以及评估算法 ( \mathrm{Eval} ) 组成，以便对于任何函数 ( f ) 和任何明文 ( m_i )，

[ \mathrm{Dec}(\mathrm{Eval}(f, \mathrm{Enc}(m_1, \dots, m_n))) = f(m_1, \dots, m_n) ]

粗略地讲，这意味着FHE方案允许对加密数据进行计算，而不需要知道其明文值。在前面的例子中，函数 ( f ) 为模2加法。需要注意的重要一点是FHE方案不依赖于函数 ( f )，这意味着任何函数都可以在加密数据上进行评估。

迄今为止，所有FHE方案的密文中都含有噪声，正如在LWE中提到的，经过一些对密文的操作后，需要引入引导（bootstrapping）操作以降低噪声。否则，解密的明文可能不正确。引导操作高度依赖于FHE方案，但基本上是对密文执行同态解密操作以降低噪声，同时仍然保持数据加密。由于解密去除了消息中的误差项，噪声得以降低。然而，解密本身也会引入一些噪声；因此，必须确保解密的结果是正确的。这通常是FHE中最耗时的部分。在后续的发展中，提出了较少消耗的引导操作以实现实际性能。

FHE的安全模型

在转到攻击之前，我们还需要覆盖的最后一件事是如何定义FHE安全模型。

IND-CPA

大多数FHE方案仅实现了在选择明文攻击下的不可区分性（ IND-CPA）安全。在这种情况下，攻击者能够选择一些明文 ( m_0 ) 和 ( m_1 ) 来请求它们的加密。挑战者选择一个随机位 ( b ) 并将 ( c_b ) （即 ( m_b ) 的加密）发送给攻击者。然后，如果攻击者能够区分密文 ( c_b ) （即猜出 ( b )），攻击就被认为是成功的。该安全模型对某些场景可能足够，但一旦攻击者获得了他们选择的一些密文的解密访问权限，就可能不安全。

IND-CCA2

对于更强的安全模型，通常希望实现自适应选择密文攻击下的不可区分性（ IND-CCA2）。在这种情况下，攻击者获得可以在任何时间使用的解密oracle，他们的目标是在先前一样区分密文。在这种情况下，攻击者可以提交密文并获得解密的明文。显然，攻击者不能请求解密他们需要区分的明文。该模型通常用于评估密码系统的安全性。例如，NIST选择的后量子密码的新标准↗的公钥加密Kyber达到了 IND-CCA2。

IND-CPAD

在FHE的情况下，情况更复杂。在 IND-CPAD 中，攻击者可以请求解密 ( c_b + c_b ) 并检查返回值是否等于两倍的明文值（即 ( m_0 + m_0 ) 或 ( m_1 + m_1 )）。因此，他们可以分辨先前接收到的密文 ( c_b ) 是哪个明文的加密。因此，如果一个加密方案具有同态属性，它就无法实现 IND-CCA2 安全性。这意味着，只要攻击者处于可以获得一些密文解密的情况下，他们就可能破坏加密的安全性。这个特性引发了一些研究，以定义FHE可达到的最大安全性和可能存在的弱点。这个问题是已知的；例如，由微软开发的SEAL库↗对用户发出强烈警告↗，关于在实际使用这些方案时可能的陷阱。

理解FHE方案的安全性无疑是一个主要关切，这就是为什么提出了 IND-CPAD 的概念，以仔细研究FHE安全性。在这个模型中，最初由Li和Micciancio↗在2021年提出，攻击者相比于 IND-CPA 具有更大的权力。D 代表攻击者观察一些解密结果的能力。像往常一样，攻击者的目标是以高概率猜测挑战者随机生成的一个位。攻击者可以请求任何明文 ( m_0, m_1 ) 的加密，并获得与挑战者选择的位 ( b ) 对应的加密。攻击者还可以请求之前加密查询的函数评估，函数由他们选择。挑战者在他们一侧存储这些查询。最后，攻击者可以请求解密，但只能针对与挑战位无关的之前查询；否则不发送输出。这意味着只有当前查询中的两个对应消息相等时，才会发送解密结果。IND-CPAD 的完整描述在李和Micciancio的论文中给出。

如果任何在上述游戏中参与的攻击者在猜测位 ( b ) 时没有统计优势，则给定方案满足 IND-CPAD 安全性。与 IND-CPA 模型相比，这个方案似乎并没有帮助攻击者。相反，当这个模型被引入时，证明一种FHE方案，即CKKS↗，并未抵抗这种模型。这篇文章中提出的两个新攻击表明这一模型并不适用于此前被假定满足 IND-CPAD 安全性的大多数当前FHE方案。

这些攻击表明 IND-CPAD 并不适合FHE方案。为FHE schema找到一个良好的安全模型仍然是一个开放问题，也是一个持续的研究领域。

针对FHE的新攻击

第一项攻击↗是由来自法国原子能委员会（CEA）的团队提出的，而第二项攻击↗则来自于公司CryptoLab↗。这两篇论文在2024年2月的Cryptology ePrint Archive上发表。

这两篇论文中的攻击利用了基于LWE的方案在加密后含有噪声这一事实。对密文进行迭代操作可能会放大噪声，直到解密后的明文本身不再正确。让我们来看一下如果我们反复将0的加密加到自身会发生什么：

sage: m = 0
sage: c = lwe.encrypt(m,s)
sage: while m == 0:
....:     c = lwe.enc_add(c,c)
....:     m = lwe.decrypt(c,s)
....:
sage: m
1

在一些迭代后，密文原本应该始终解密为0，但错误地解密为1。在这种情况下，我们仅遵循 IND-CPAD 游戏的规则，因为明文的评估始终输出零。这意味着，建立在此属性上的成功攻击将破坏FHE方案的 IND-CPAD 安全性。

让我们看看内部发生了什么。我们添加了一个详细模式，以打印以二进制形式解密出错的值：

sage: c = lwe.encrypt(0, s, verbose=True)
e = 3 (0000000000000011)
sage: c = lwe.enc_add(c,c)
sage: m = lwe.decrypt(c, s, verbose=True)
e = 6 (0000000000000110)
sage: c = lwe.enc_add(c,c)
sage: m = lwe.decrypt(c, s, verbose=True)
e = 12 (0000000000001100)
sage: m
0

我们看到，错误项在每次加法操作后都翻了一倍，这与之前看到的密文相加的公式是一致的。这种情况持续，直到消息本身被错误项损坏。现在我们有了一种恢复错误项的方式，我们将零的密文加到自身，直到解密消息变为1。然后，通过二分查找↗，可以恢复错误的绝对值 ( |e| )。CEA提出的攻击使用此方法恢复多个值 ( |e_i| )。然而，该攻击实施未提供，因此我们在仓库的脚本binary_attack.sage中实现了二分查找：

sage: attach("binary_attack.sage")
sage: c = lwe.encrypt(0, s, verbose=True)
e = -2 (-000000000000010)
sage: e, last_c = recover_abs_e(c, s)
sage: e
2

我们需要将秘密密钥 ( s ) 传递给函数，因为它需要请求解密明文，这符合 IND-CPAD 模型。正如预期的那样，该函数返回错误的正确绝对值 ( e )。

然后，该攻击使用一个技巧来确保所有恢复的值 ( e_i ) 具有相同的符号，并丢弃其他与之相反符号的值。最初，得到足够多具有相同符号的 ( e_i ) 后，依赖解密公式关系建立线性系统：

[ \langle a_i,s \rangle = b_i + |e_i| ]

线性系统可以被解以恢复秘密密钥 ( s )。由于错误项知道其符号， ( s ) 的值有两种可能性。我们的脚本在函数 binary_attack 中实现了这些步骤：

sage: s_recovered = binary_attack(s)
sage: s_recovered == s
True

我们在脚本中稍微改进了攻击，未丢弃b正负号不同的错误项，但我们应该相应地调整线性系统。当错误符号相同时，保持线性方程与之前相同：

[ \langle a_i,s \rangle = b_i + |e_i| ]

当它们不同的时候，向线性系统中添加以下方程：

[ \langle a_i,s \rangle = b_i - |e_i| ]

这使得减少攻击所需操作数量一半。

然后，在CEA的论文中，攻击针对环LWE（RLWE）方案。在这种LWE的变体中，消息位 ( m0,…,m{n-1} \in \mathbb{Z}_2^n ) 被视为在环 ( R_q = \mathbb{Z}_q [X] / (X^n + 1) ) 上定义的多项式的系数。该攻击是在上述针对LWE方案攻击的直接改编。它旨在一个消息系数上，采用之前相同方法进行。另一项攻击↗（CryptoLab团队提出）使用类似的方法针对RLWE进行攻击。如论文中附图所示，当噪声放大到某一程度时，消息解密会发生变化。

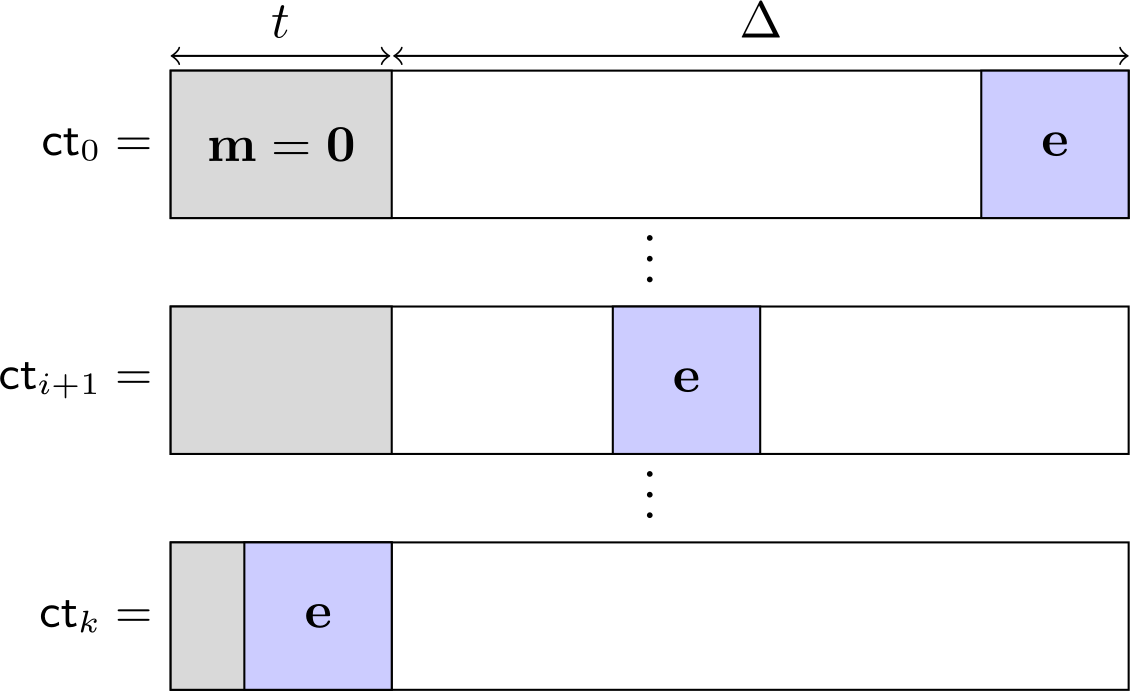
当误差过高时，结果可能错误，从而能够用类似于之前为LWE所示的方法恢复错误值。

实际结果

一些基于RLWE构建的实际FHE方案包括Brakerski/Fan-Vercauteren↗（BFV）、Brakerski、Gentry和Vaikuntanathan↗（BGV）和在圆周上快速全同态加密↗（TFHE）密码系统。它们在明文和密文编码的选择及执行功能评估方面有所不同。

对BFV的结果

第一项攻击的作者声称成功攻击了SEAL的BFV密码系统实现、OpenFHE↗和Lattigo↗库，安全参数在217位到256位之间。据报告，这些攻击在标准机器上完全恢复密钥的时间从几分钟到几个小时不等。第二篇论文的攻击也成功应用于OpenFHE的BFV实现，作者在其GitHub仓库↗中提供了概念验证实现。这使得能够轻松测试针对库的攻击。

对BGV的结果

第一篇论文还报告了对SEAL和OpenFHE的BGV密码系统实现的成功攻击，结果与BFV类似。作者还尝试用相同的方法攻击HElib↗，但未能成功。HElib实施了一种监控噪声水平的对策，禁止解密噪声级别过高的密文。

对TFHE的结果

最后，两个攻击都针对了TFHE。在第一篇论文中，作者对TFHElib↗施加了攻击，该库允许在没有引导的情况下添加密文，发现攻击成功，耗时不到一秒。

为了快速概述每个方案的攻击需求，我们将CEA论文中的结果表复制到此：

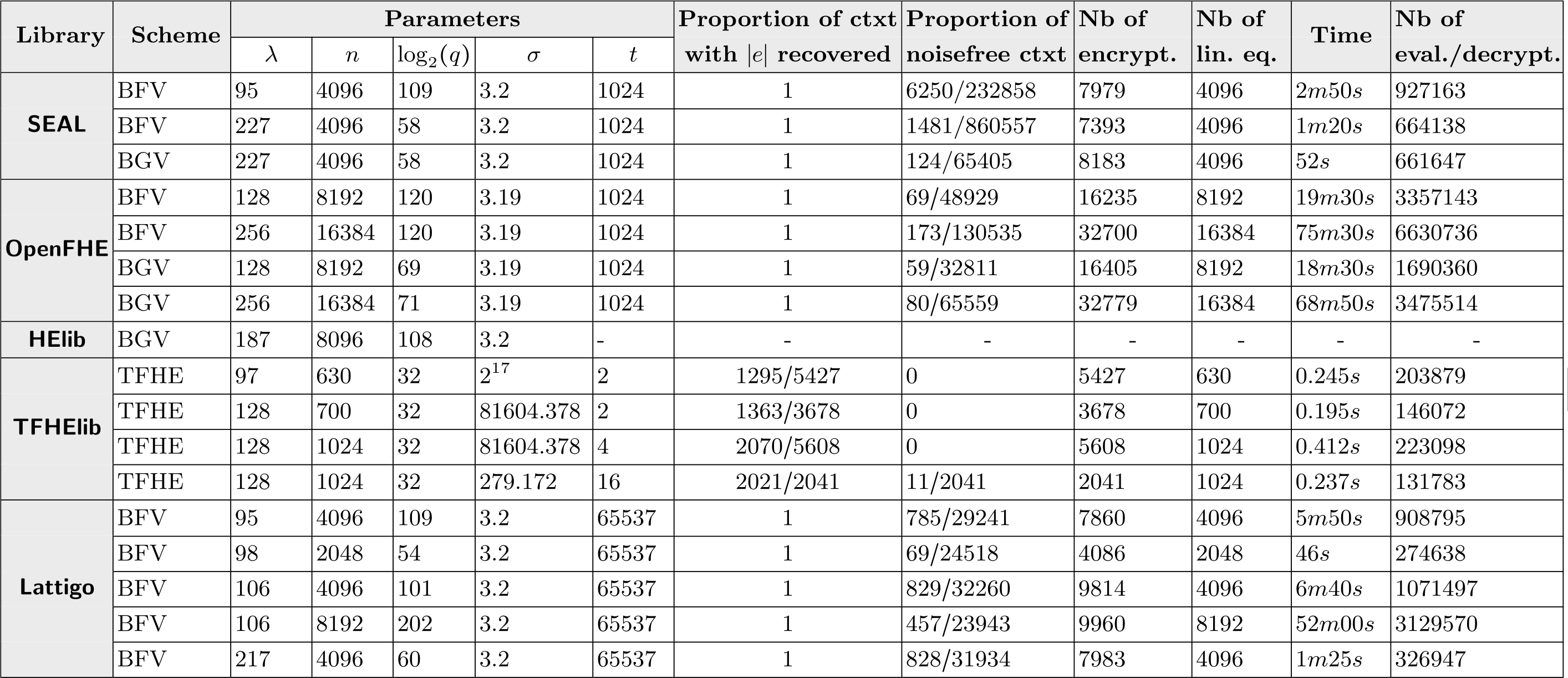
这显示出攻击在常见安全参数下确实是可行的。它还表明，向攻击者开放FHE密文的解密会导致密钥恢复攻击，这些攻击非常实际。

对TFHE-rs的概念验证

第二篇论文目标是Zama开发的Rust库TFHE-rs↗。这里的攻击与之前稍有不同，因为该库在每次操作后执行门引导以降低噪声。仅在两次AND评估之后，才利用解密失败。当解密失败时，返回的错误项具有与密钥位值相关的统计分布，因此可以恢复。第二篇论文的作者还提供了针对TFHE-rs版本0.5.4的攻击实现。

执行攻击的主要代码如下：

// --- 评估oracle ---
// 同态评估
// 获得引导后发生错误的密文
let ct_bts: Vec<_> = ct_arr.par_iter().map(|x| server_key.and(x, x)).collect();

// 对同一密文再次应用AND门
let ct_out: Vec<_> = ct_bts.par_iter().map(|x| server_key.and(x, x)).collect();

// --- 解密oracle ---
let res: Vec<_> = ct_out.par_iter().map(|x| client_key.decrypt(x)).collect();

// 输出解密失败密文的系数
for r in 0..ARRAY_SIZE {
    if res[r] == false {
        nb_failures += 1;
        let ct = &ct_bts[r];
        match ct {
            Ciphertext::Trivial(_b) => { println!("triv;");},
            Ciphertext::Encrypted(lwe_ciphertext) => {
                let (mask, body) = lwe_ciphertext.get_mask_and_body();
                println!("Mask {:#?}", mask);
                println!("body {:#?}", body);
            }
        }
    }
}

这个想法是对密文进行两次AND评估，并在发生解密失败时收集这些失败。攻击实现使用非默认参数，目标仍然是128位安全级别。在我们的仓库的tfhe文件夹中，我们创建了原始论文实现的副本，并进行了小幅修改，以简化解密失败的收集。收集阶段可以通过以下命令运行：

cargo run --release > ../failures.out

完整收集失败的过程不到四小时，标准笔记本即可恢复近20,000次解密失败。然后，使用Python脚本main.py执行对恢复秘密密钥位的统计。脚本mainplot.py展示结果：

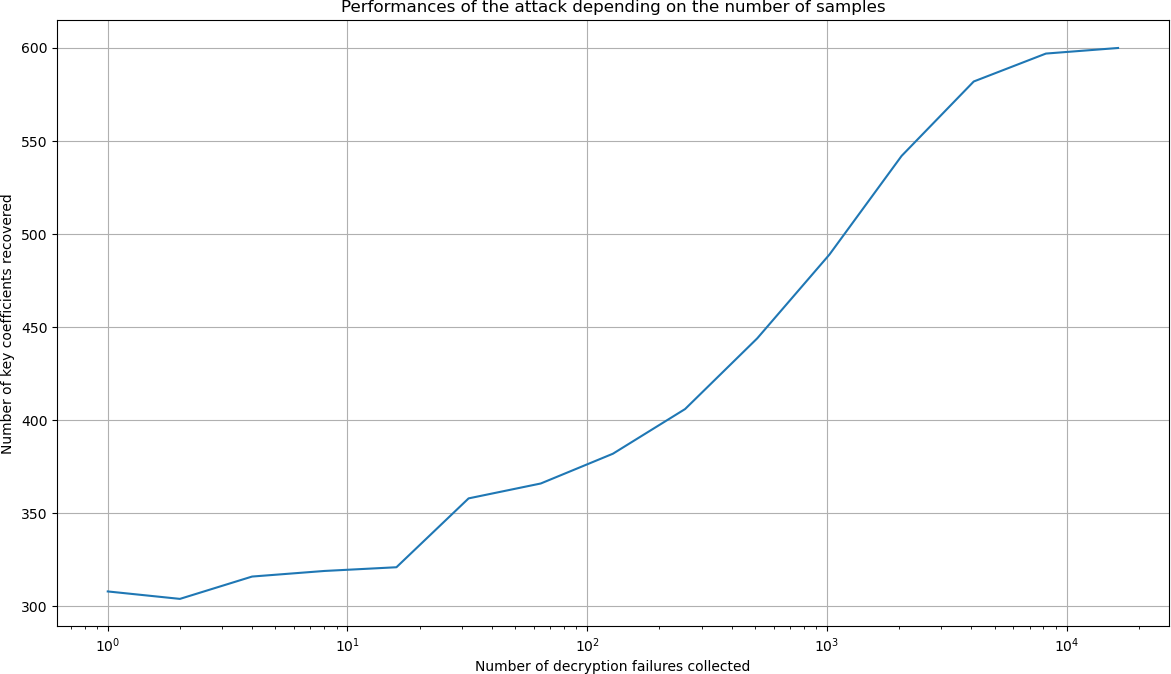
它绘制了恢复的密钥系数数量与获得的解密失败次数的关系。对于先前选择的参数，经过获得约20,000次解密失败后，所有600个密钥系数都已恢复。这证明了对于此参数选择的攻击的可行性。对于默认参数，作者解释道，攻击将需要超过300年。因此，在这种情况下，它可能不那么关键，但仍取决于攻击者可用的力量而受到关注。

关于门限同态加密的影响

在FHE之上，可以构建一种门限解密方案。门限解密意味着在n位用户中，密文仅在至少t位用户合作并遵循协议步骤的情况下才能解密，从而解密密文。然而，少于t个用户的子集将无法解密密文。例如，Zama的fhEVM↗使用一组拥有秘密份额的验证器，一旦t个验证器同意解密数据，他们一起运行门限解密，从而获得明文数据。然而，未经任何验证器访问的秘密解密密钥。如果没有这样的方案，节点可能独自决定通过解密数据来破解智能合约的机密性。

在门限解密设置中，密文使用解密秘密密钥进行解密，而该密钥对所有用户都是未知的。在协作解密协议结束时，每个用户获得解密结果。就在这种情况下，前面描述的攻击可能适用以恢复全局秘密密钥。尽管应用前的攻击所需的解密数量巨大，但它们可能在该配置下构成威胁，并需要实施一些对策。CEA论文表明，在Lattigo实现上应用需要大量解密的攻击可能性以及应对策略。CryptoLab论文则讨论了基于TFHE的门限加密↗可能面临攻击。这些攻击需在实际部署此类方案时加以考虑。

结论

这篇文章回顾了用于FHE构建的通用概念和主要安全模型。我们也看到了FHE的安全模型尚未完全解 understood。尽管现代FHE已证明为 IND-CPA，但向攻击者开放的解密访问可能会导致灾难，正如最近针对 IND-CPAD 安全模型的攻击所示。这些攻击适用于大多数广泛可用的实现。

通过在Sage中简单的玩具实现，我们展示了这些攻击的内部工作原理。本文示例的完整实现可在GitHub↗上找到。我们希望这有助于理解披露FHE解密的风险，并在实践中提高此类方案的安全性。FHE领域发展迅速，我们期待关于其安全性的最新进展。

关于我们

Zellic专注于保护新兴技术。我们的安全研究人员揭示了在财富500强和DeFi巨头等最有价值目标中的脆弱性。

开发者、创始人和投资者信任我们的安全评估，以快速、自信地发布产品，同时没有关键漏洞。凭借我们在实际攻击性安全研究中的背景，我们发现其他人遗漏的内容。

‍ 联系我们↗，进行比其他竞争对手更好的审计。真正的审计，而非走过场的审核。

• 原文链接： zellic.io/blog/fhe-secur...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～