多方计算解读：安全数据协作

多方计算 (MPC)：安全、私密的协作

了解多方计算 (MPC) 如何在不暴露私人数据的情况下实现安全协作。学习它的历史、安全模型和应用。

什么是多方计算 (MPC)？

多方计算 (MPC) 是 加密技术 的一个子领域，专注于安全计算，使多个参与者在保密各自数据的情况下进行计算。每个参与者只会看到最终结果，而不会看到其他人的输入。MPC 结合了计算、验证（以检测作弊）和隐私保护的加密协议。

想象三家公司被指派计算各自的平均收入，而不向对方透露实际数字。MPC 允许他们计算平均值，每家公司只看到最终结果，而不会看到其他公司的收入。

虽然零知识证明（ ZKPs）和多方计算 (MPC) 都属于隐私保护加密，但它们的目标不同。ZKPs 允许一方证明对秘密的知识而不揭示它（例如，通过在不透露任何敏感凭据的情况下证明身份），甚至在多方环境中也是如此。然而，MPC 使多个方能够共同计算其私有输入上的函数，而不会暴露输入本身。

多方计算的关键突破是，参与方可以在不向任何人揭露其数据的情况下协作进行计算。

历史

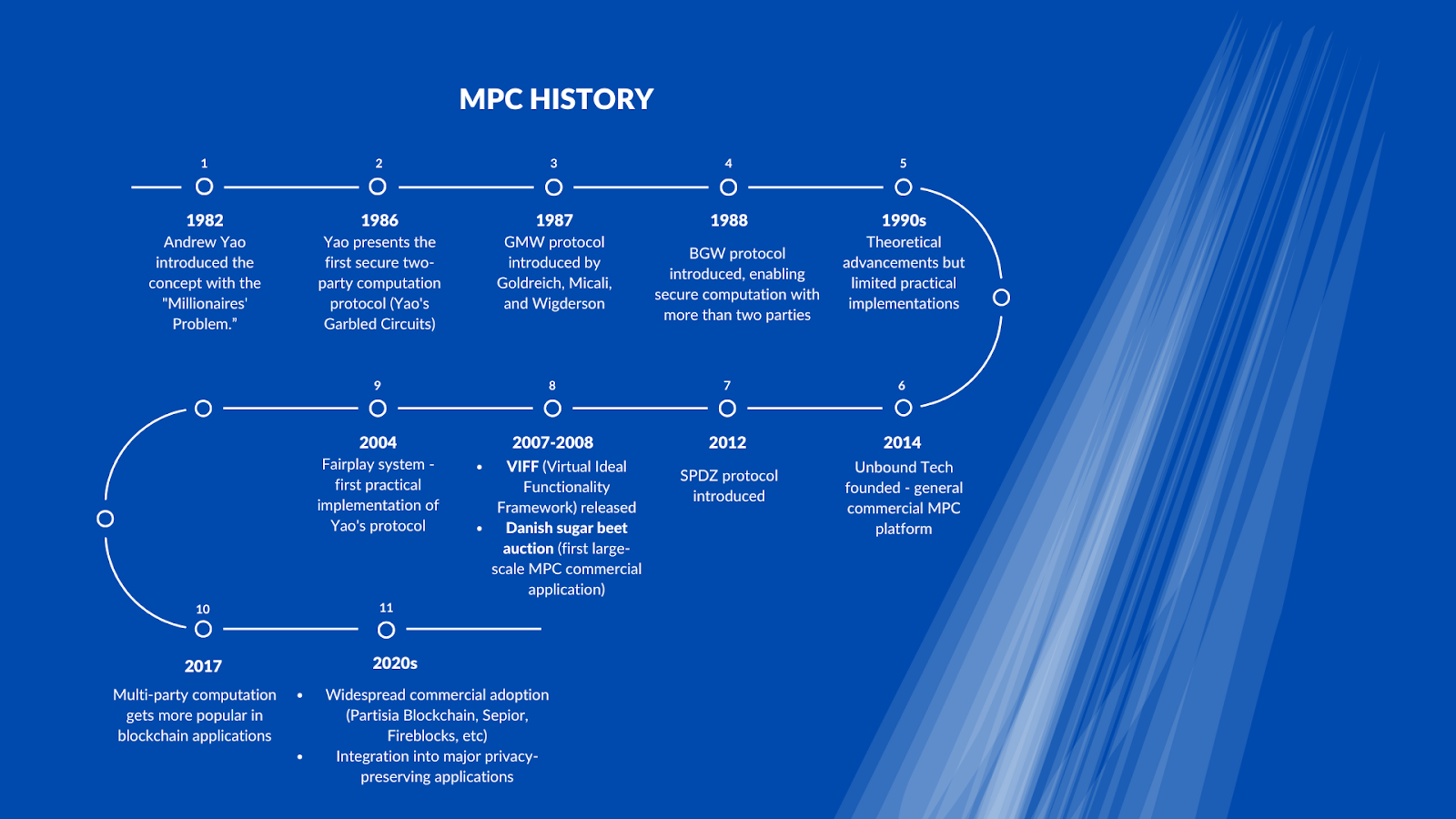
多方计算在1980年代作为一个理论概念在加密学中出现，但其实际应用花了数十年才得以实现。以下是其发展过程中的关键里程碑——从早期协议如 姚期智的误导电路 到现代 区块链 集成。这个时间线突出了 MPC 如何从学术研究过渡到实际的隐私解决方案。

核心概念

隐私保护

多方计算通过数学保证确保输入隐私。该协议在数学上防止参与者学习其他人的输入，同时仍允许对这些输入进行计算。

分布式信任

没有单一方持有所有数据或控制计算。多方计算的安全性来自于将信任分布在多个参与者之间，从而使其对个别妥协具有抗击打能力。

那么，这一切重要吗？让我们探索一下为什么 MPC 对今天的隐私需求至关重要。

MPC 的重要性

MPC 解决了数据隐私的一个特定问题：如何在不暴露敏感数据的情况下进行计算。这很重要，原因有几个：

1. 数据隐私法律：组织必须在遵守如《通用数据保护条例》（ GDPR）和《加利福尼亚消费者隐私法》（ CCPA）等法规的同时分析数据。

2. 跨组织协作：公司可以在不共享机密信息的情况下合作。

3. 单点故障：传统系统在单一位置收集和集中数据，导致安全风险。

4. 信任最小化：MPC 消除了对单一受信第三方的依赖。例如，组织可以在不共享原始数据的情况下进行协作，而加密系统（如 ZKP 受信设置）能够在没有中央权威的情况下安全地生成公共参数。

但 MPC 如何防范潜在威胁呢？让我们看看其安全模型。

理解 MPC 安全模型

MPC 中的对手是什么？

在 MPC 协议中，“ 对手”是指试图破坏协议安全性的参与者（或参与者组）。对手是系统中的坏行为者。他们可能是：

• 外部攻击者，试图获取私人信息
• 在协议中不遵循规则的参与者
• 被妥协的各方（如被黑客攻击的服务器）

因此，MPC 协议围绕两个基本问题进行设计：

1. 对抗设置：在协议的安全保证失败之前，可以有多少个参与者被败坏？ _( 备注 : 通常在学术论文中被称为 " 设置 "。) 示例：一个设计用于不诚实多数设置的协议（ 下面会解释）数学上被保证即使在 5 个参与者中有 4 个被败坏的情况下仍然保持安全。

2. 对抗行为：各方可以使用什么策略来攻击系统？ 示例：被动观察者可能能够推断出私有数据，而主动攻击者则可能伪造输入或串通。

这些问题定义了协议对串通（例如，多个被妥协的方秘密地共享数据以侵犯隐私）的抵抗能力，以及应对对抗性行为如窃听（拦截消息以推断私有输入）或破坏（故意中断计算）的能力。

安全模型描述了这些对手可能的行为以及协议对其保护的方法。多方计算中的一些主要安全模型包括：

半诚实安全模型（被动 / 诚实但好奇）

意思：

半诚实安全模型假设对手遵循协议规则，但试图从交换消息中推断私有信息。一个对半诚实对手安全的协议（称为 半诚实安全 协议）确保各方 不能 推断私有输入，即使他们被动地分析协议交互。

它是如何工作的：

半诚实安全协议使用 误导电路 和秘密分享方案（ 后面讨论）等加密原语，确保没有单一方能够在没有协作的情况下重构私有数据（例如，获得足够的秘密份额）。

用例：

1. 银行使用 MPC 进行欺诈检测：半诚实安全使多家银行可以协作分析交易数据并识别欺诈模式，而无需暴露客户记录。半诚实协议为被动对手提供了安全，同时保持了处理大规模数据集所需的计算效率。

2. 医学研究合作：半诚实协议允许医院共同分析患者基因组，同时保持隐私。这些协议通过最小化计算开销，仍然适用于数据密集型任务，如基因组研究。

半诚实安全的好处：

• 效率：通常比恶意安全协议需要更少的加密验证步骤（例如，不需要零知识证明或 切换选择）。

• 较低的开销：相较于主动对手模型，计算成本降低。

• 可扩展性：理想于参与者被激励合作的应用（例如，互利的数据分析）。

恶意（主动）安全模型

意思：

恶意安全模型假设对手可能随意偏离协议：发送虚假输入，篡改计算，或提前终止以破坏结果。一个 恶意安全 协议在某些参与者作弊的情况下保证隐私和准确性，确保输出有效且输入保持机密。

它是如何工作的：

恶意安全协议包括额外的加密验证步骤（例如，零知识证明、切换选择、认证秘密分享 MAC），能够数学上检测并防止作弊。它强制各方在每个步骤都证明他们正确遵循协议，确保输入隐私和计算完整性，即使面临主动攻击者。

用例：

1. 投票系统：恶意安全确保没有方可以提交无效选票（例如，投票给不存在的候选人）或操控计票。例如，ZK 证明可证明投票是有效的（例如，为注册候选人）而不透露个人选择。

2. 加密货币：门限签名要求恶意安全以防止对手在密钥生成或窃取资金过程中施加偏见。检查保证 私钥 从未在单一地点重构。

恶意安全的好处：

• 更强的安全性：即使对手干扰协议，隐私和准确性也得到保证。

• 威慑效果：作弊要么被检测到（例如，如果检测到无效的 ZK 证明，诚实的一方会终止协议），要么在加密上变得不可能。

• 高风险适用性：这对金融清算等应用至关重要，因为错误或泄露可能导致严重后果。

其他安全模型，例如 隐蔽安全，在半诚实和恶意安全之间提供一个中间地带，但这两种是使用最广泛的。

这些安全模型定义了协议如何处理对手。让我们检查决定其实施的设置：

MPC 设置

1. 不诚实多数：

• 即使只有一个参与者是诚实的，安全保证仍然有效；在 5 方系统中，即使 4 方被腐败，协议仍然保持安全。

• 与诚实多数相比，这是最保守的安全假设，因为它假设大多数参与者是恶意的。

• 被 SPDZ 等协议使用。

• 不诚实多数协议由于额外的安全措施的要求，通常会有更高的计算和通信开销。

2. 诚实多数：

• 当大多数参与者是诚实时，安全保证有效；在 7 方系统中，至少 4 方必须诚实。

• BGW 协议是一种特殊情况，要求更多的诚实参与者：对于恶意安全，少于三分之一的参与者可以被腐败（例如，在 7 方系统中至少需要 5 个诚实参与者）。

• 与不诚实多数相比，通常实现更高的效率和较低的通信复杂性。

3. 基于门限：

• 安全性依赖于一个门限（例如，在 4 方系统中，50% 诚实的参与者）。

• 在安全与效率之间提供灵活性的方法。

流行的 MPC 协议

1. BGW：BGW （Ben-Or, Goldwasser 和 Wigderson）协议于 1988 年推出，是多方计算的基础。它是一个安全的 MPC 协议，允许一组方共同计算一个函数，同时保持输入的私密性。它扩展了香农秘密分享（请参见下述解释）并结合加密技术，使得在私有输入上进行安全的多方计算成为可能。 BGW 对于半诚实对手安全（如果少于一半的参与者被腐败）和恶意对手安全（如果少于三分之一的参与者被腐败）。

2. GMW：GMW （Goldreich, Micali 和 Wigderson）协议于 1987 年推出，是一种经典的 MPC 协议，使用布尔电路表示法。当计算一个函数时，它将计算分解为逻辑运算（如 AND、OR、NOT 门），并逐步处理加密数据。它主要针对忠于协议却试图从接收到的消息中学习额外信息的半诚实对手是安全的。GMW 协议使用 无关转移 等技术，确保每方只学习从计算中应该学习的内容。

3. SPDZ：SPDZ （Smart, Pastro, Damgård 和 Zakarias）协议于 2012 年开发，代表了实用 MPC 的重大进展。SPDZ 采用加法秘密分享（将秘密分割成随机数，让其和等于原始秘密）并结合 基于 MAC 的检查（用于确保数据完整性的加密标签），以确认参与者正确遵循协议。SPDZ 需要一个预处理阶段（提前准备加密材料），并在在线计算阶段（实时执行）中实现了高性能。它对恶意对手保持安全，这意味着即使参与者积极试图作弊，仍然保持安全。

现在，让我们探讨如何通过秘密共享实现安全计算。

多方计算中的秘密共享

秘密共享允许将一个秘密分成多个部分，称为份额，其中：

• 每个参与者接收一个份额
• 单个份额对秘密毫无透露
• 组合足够的份额即可重构秘密

在门限秘密共享方案中：

• n：将秘密分割成的总份额数（例如，5）。
• t：门限 - 重构秘密所需的最低份额数（例如，3）。

例如，请参见以下香农秘密共享的例子。

常见的秘密共享方案：

1. 香农的秘密共享

• 使用有限域上的多项式将秘密分割成份额。在重构时使用 拉格朗日插值法：份额的门限唯一地确定多项式（从而确定秘密）。较少的份额无法透露任何信息——就像需要足够的点来定义一条曲线。

• 灵活的门限方案：经过任何 t 份额（总份额为 n）即可重构秘密，其中多项式是 t-1 次，从而在少于 t 份额的情况下确保安全性。

例如，在 3-out-of-5 方案中：

• 秘密被分为五个总份额
• 任何三个份额都可以重构秘密
• 两个或更少的份额不会透露任何信息

这类似于一个拼图：你需要足够数量的拼块（"门限"）来解决它，但单独的拼块没有用。

2. 加法秘密共享

• 将秘密分割成与秘密和相等的随机份额。
• 需要所有份额进行重构（如果分为 n 份额，则门限 t 等于 n）。
• 用于 SPDZ 等协议。
• 对于线性计算（例如加法、平均）比非线性计算更高效。

示例：如果秘密是 10，份额可以是 3、5 和 2（3 + 5 + 2 = 10）。必须组合所有份额才能恢复秘密。

区块链中的 MPC 钱包

与传统加密货币钱包（存储单一私钥）不同，MPC 钱包将密钥生成和签名分散到多个独立方之间。当用户签署交易时，这些方借助加密协议协作创建签名，而无需访问完整的密钥。

这种方法消除了传统钱包存在的单点故障。在某个位置没有一个可以被盗或丢失的单一私钥。如果一个设备被妥协，资金仍然保持安全，因为攻击者必须同时妥协多个方。这一安全模型还通过允许用户添加或移除设备、设定多个审批要求等方式，实现了更灵活的密钥管理。

MPC 钱包的例子包括：

• ZenGo: 使用多方计算进行私钥管理的无钥加密钱包。

• Fireblocks: 一个企业级数字资产平台，使用 MPC。它为像 Revolut 这样的机构提供数字资产安全。

MPC 钱包中的门限签名

MPC 钱包使用门限签名，其中：

• 私钥被分割成份额。
• 必须满足特定数量的份额（门限）才能签字。
• 签名在数学上与常规签名相同。
• 验证者无法辨别是否通过 MPC 创建。

示例：在 2-of-3 门限方案中，必须有两个方协作签署——一个方无法单独操作。

多方计算与多签名钱包的区别

多签名钱包 需要多把私钥；每个方持有自己的完整密钥并独立签名。相比之下，MPC 钱包通过秘密共享将单一私钥分割成份额。没有一个方持有完整密钥，必须协作才能生成单一签名。结果是一个标准数字签名，在区块链上与其他签名没有区别。

在讨论完 MPC 钱包的工作原理后，接下来让我们探索它们更广泛的应用——今天和未来。

MPC 用例

数字资产保管

MPC 使得加密货币在区块链钱包中的安全密钥管理成为可能：

• 私钥被分成多个份额
• 没有任何单一方可以单独访问或使用这些密钥
• 交易需要合作
• 如果有一方被妥协，攻击者无法访问完整密钥，从而保护了资产。

隐私保护分析

MPC 使组织能够从共享数据中获取见解而不暴露个别输入。例如：

• 波士顿女性劳动力委员会: 与大学合作使用 MPC 分析性别薪酬差距，同时保持个人薪资数据私密。

• 丹麦甜菜拍卖（2008 年）: 第一个大规模商业 MPC 应用，农民在不揭示出价的情况下计算公平价格。

隐私保护机器学习

MPC 能够实现协作 AI 训练，而无需共享原始数据：

• Meta（Facebook）：Meta 的研究团队正在 探索 MPC 框架，以在保留用户隐私的同时，在去中心化数据集上训练机器学习模型。

零知识证明受信设置仪式

MPC 安全生成加密系统的参数（例如 ZKP 受信设置），确保没有单一方能够学习敏感参数：

• Zcash Sapling 仪式: 使用 MPC 生成零知识证明的公共参数，防止任何单个参与者破坏系统。

MPC 的未来

多方计算的核心优势——在不暴露数据的情况下实现协作——可以满足需要保密的领域中的复杂需求。例如：

• 医疗：医院可以针对跨院研究（例如癌症研究）进行协作，保持基因隐私而不共享记录。

• 金融：银行可以共同筛选交易以防止洗钱，并在不透露客户细节的情况下评估信用风险。

• 供应链：公司可以全球审计供应商，同时保护商业机密。

结论

多方计算从1980年代的理论概念演变为如今解决实际隐私挑战的实用技术。它处理敏感数据而不暴露，提高了跨行业的新可能性，从帮助医院协作进行医学研究到实现更安全的加密货币钱包。

虽然 MPC 并不是解决每个隐私问题的魔法解决方案，但它使得多个方能够在不直接共享数据的情况下进行协作。随着隐私问题的加剧和法规的日益严格，MPC 在实现金融上的安全协作的角色可能会变得更加关键。

• 原文链接： cyfrin.io/blog/multi-par...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～