什么是零知识证明 | 给程序员的实用指南
- Cyfrin
- 发布于 2024-10-10 22:39
- 阅读 2105
零知识证明(ZKPs)是一种加密技术,允许一方在不暴露具体信息的情况下证明其对该信息的知识。文章深入探讨了ZKPs的工作原理、种类及其在区块链应用中的作用,旨在帮助程序员理解如何实际实现这一技术,并涵盖了交互式和非交互式证明、关键组件以及信任设置等重要概念。
零知识证明(ZKP)是什么,它是如何工作的?探索零知识证明,调查数学零知识证明,并了解程序员需要知道的实现内容。
区块链的设计是透明的。但在我们需要数据保密的情况下怎么办?例如,我想证明我的年龄而不透露我的生日?或者证明我确实是我所说的人,而不透露我的身份。或者证明我拥有贷款所需的担保。这里就涉及到零知识证明。
零知识证明使实体能够证明其知道某个信息,而不透露该信息本身。
本文探讨零知识证明(ZKP)的概念,解释其工作原理,并提供示例以说明你需要了解的知识,所有内容均在区块链技术的背景下进行。它针对希望理解数学零知识证明高层概述以及实际如何工作的程序员。
对于那些不感兴趣详细分析而更喜欢高层解释的人,Jarrod Watts在这篇出色的文章中提供了使用实践非数学示例的零知识证明的高层描述。
零知识证明是什么?
零知识证明(ZKP)是加密证明,允许你证明对某事物的知识,而不透露该事物本身。为了做到这一点,算法零知识系统使用一些数据作为 输入,并返回输入是否满足 特定要求。例如,证明我拥有解锁保险箱的秘密密码,而不透露密码。
参与零知识证明有 两个角色:
- prover:想要证明其知道一个秘密,而不透露秘密本身的实体。他们根据这个知识生成一个证明,验证者可以检查。在我们的保险箱示例中,这将是证明他们知道密码的人(或实体)。
- 验证者 是负责验证证明的实体。验证者在不了解秘密的情况下注确认证明的有效性。同样,在我们的保险箱示例中,这将是验证证明者密码是解锁保险箱所需的密码的人(或实体)。
交互式和非交互式 ZKPs
零知识证明有两种主要类型:交互式和非交互式 ZKP:
交互式零知识证明:
- 需要 prover 和验证者之间的多轮通信,以交换信息并验证证明。
- 验证者通过向 prover 发送挑战并接收响应来积极参与过程。
- 不适合区块链应用,因为需要重复的交互是不切实际的。
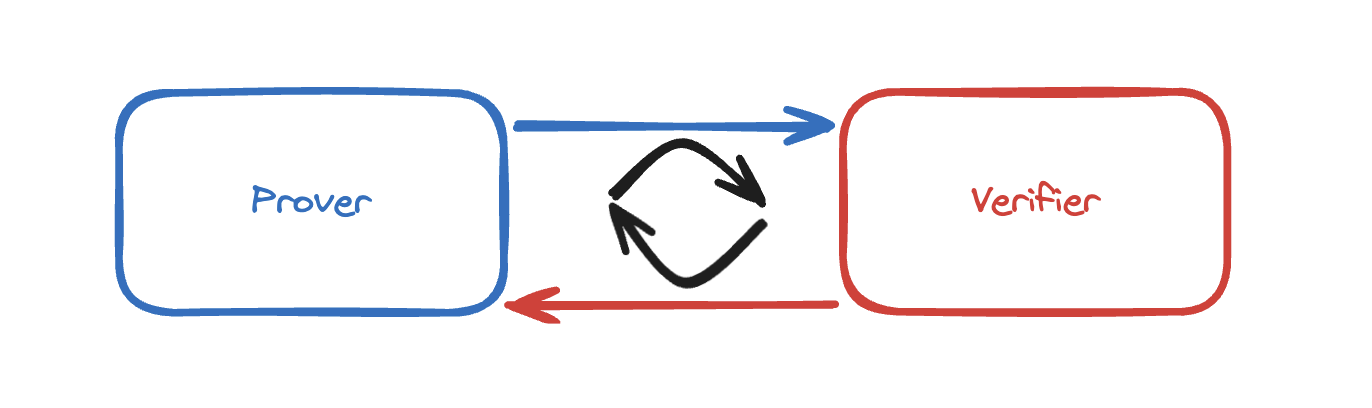
在交互式零知识证明中 prover 和验证者之间如何互动。
非交互式零知识证明:
- 涉及从 prover 到验证者的 单条消息,其中包含所有必要的证明信息。
- 不需要验证者和 prover 之间进一步的交互;验证者可以独立检查证明。
- 非交互式零知识证明非常适合区块链应用,因为它们减少了通信需求,提高了效率,并且可以被网络上的任何参与者验证。因此,它们支持无信任验证,便于智能合约和去中心化协议的集成。
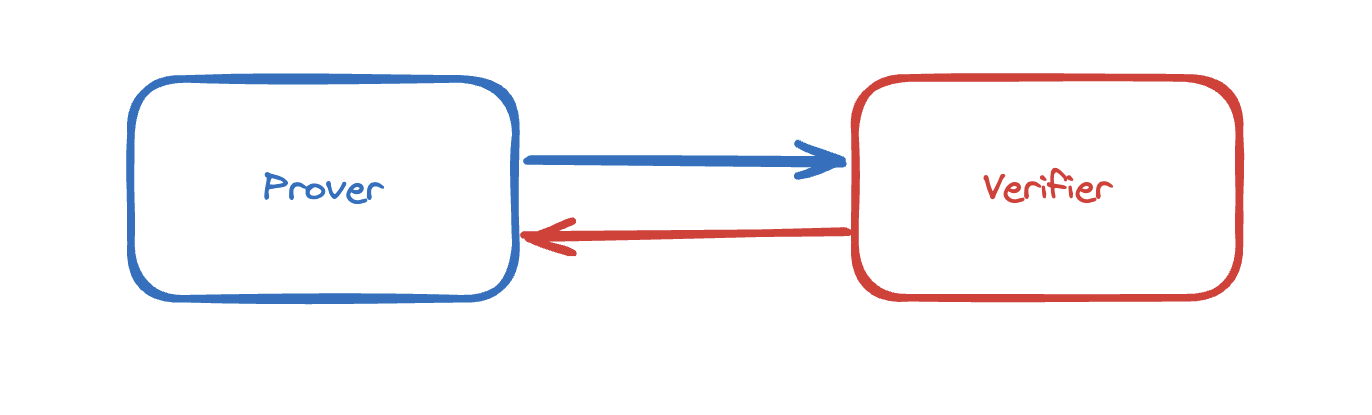
在非交互式零知识证明中 prover 和验证者之间如何互动。
零知识证明的要求
一个 ZK 证明必须满足以下标准:
- 完整性:如果输入是有效的,证明必须始终使验证者信服。
- 健全性:对于 prover 来说,使用无效输入欺骗验证者在实际操作中必须是不可能的(好吧,99.999999% 不可能)。
- 零知识性:验证者(或任何观察者)对秘密一无所知,只知道输入满足证明。
零知识证明包含三个元素:
- 见证:证人所知道并用来证明某个声明为真的秘密信息或数据。例如,在方程 x+2=3 中,见证将是 x=1。通常,这是一个输入数组,供电路使用。
- 声明/主张:证明者关于见证的声明。例如,“我知道一个满足条件的 x,x+2=3。” 单个要求被称为约束。约束的集合构成了证明者所做的声明的电路。
- 证明:由证明者生成的实际加密证明,验证者检查以确认声明,而无需透露见证本身。
零知识证明系统的类型
SNARK(简洁非交互式知识论证)是一类广泛的零知识证明系统,属于非交互式(即 prover 和验证者之间没有往来互动)。它们在证明大小和验证时间方面效率高,无论问题大小如何。
- SNARKs 需要一个 可信设置 (稍后将定义),在此过程中,使用秘密生成一组初始参数,以将见证和电路保密。如果该秘密被泄露,所有使用该设置生成的证明的安全性将遭到破坏。
- 许多 SNARK 使用 椭圆曲线密码学(ECC) 来创建证明,这依赖于离散对数问题(DLP)的难度。椭圆曲线(EC)本质上是用于密码学的复杂曲线,因为数学运算更高效,但现在不必过于担心这一点。这种对椭圆曲线的依赖使它们对未来量子计算的发展有所敏感,因为量子计算机能够解决 DLP。
- ZK SNARK 证明系统的示例:
STARKs(可扩展透明知识论证)使用一个设置过程,不依赖于秘密参数。相反,它利用哈希函数和公开的随机性来构建证明,使得设置“透明”且无需信任。由于 ZK STARKs 依赖哈希函数而不是椭圆曲线,因此它们具有抗量子计算的特性。
SNARKs 与 STARKs
在特定实现中选择 SNARKs 或 STARKs 取决于应用。比较二者:
| 验证时间 | 证明大小 | 量子抗性 | 可信设置 | 证明生成时间 | |
|---|---|---|---|---|---|
| SNARKS | 由于证明大小较小,因此计算负担更轻,验证更快。 | 在带宽和存储效率方面更小且更高效。 | 依赖于 ECC,这取决于 DLP,因此在量子计算上不具抗性。 | 需要一个可信设置,这可能会受到损害。 | 由于需要可信设置,证明生成更具计算成本,因此在需要多次证明时扩展性更差,具体取决于实现。 |
| STARKS | 由于证明大小与计算大小成对数关系,通常更慢。 | 由于使用哈希函数而不是椭圆曲线,因此更大。 | 依赖于哈希函数和随机性,使其具备量子抗性。 | 不需要可信设置。相反,它们使用一种依赖于公共随机性和哈希函数的透明设置。没有需要保护的秘密。 | 由于透明设置和所使用的更简单密码原语,证明生成更加高效和可扩展。 |
在本文的其余部分,我们将重点关注 SNARKs,因为它们在区块链生态系统中最常用。
零知识证明的关键组件
让我们来了解一些与 ZKP 相关的关键术语,以便你在看到它们时能理解它们的含义。
- 约束是描述各种输入和输出之间关系的数学规则或条件。所有约束都必须为真,以便证明有效。例如,一个约束可以指定特定输入的平方等于给定输出(如 x²=y)。必须对零知识证明系统所需的特定约束系统给予高度关注;因此,电路必须以特定格式编写。例如,Circom 针对 Groth16,需要基于 R1CS 的电路。
- 电路是将计算问题结构化表示为一系列方程或算术运算。在零知识证明系统中,证明者利用电路证明他们知道符合所有约束的一组输入,而不透露输入本身。
- 约束系统
- Rank 1 约束系统(R1CS):一种用于 Groth16 的约束系统,能够将代数电路表示为向量和矩阵的集合,然后转换为多项式。
- PLONKish:用于 PLONK 协议的约束系统,使得能根据一个矩形矩阵来定义一个代数电路。
- 算术化 是将计算问题转换为使用的约束系统所规定的电路形式的过程。例如,对于 R1CS 系统,问题需要转换为最大度数为二的多项式系统。
可信设置
可信设置是创建 ZKP 的初始阶段,其中生成一组参数。此设置要求信任,因为如果这些参数被破坏或操纵,整个系统的安全性可能面临风险。
- 有毒废物:在可信设置阶段生成的随机值,如果被破坏,则允许伪造无效证明。它们使用后必须安全地销毁。
- 通用参考字符串(CRS):这些是证明者和验证者可用的公共参数,用于创建和验证证明。
- 结构参考字符串(SRS):这是一种包含结构化数据的 CRS。例如,从秘密值(τ)幂中导出的椭圆曲线点(更多内容随即深度讨论)。
- 多方计算(MPC):在 ZKP 和可信设置的背景下,MPC 指在设置仪式中多个方共同贡献某些随机性(有毒废物的实例!)。这通过减少所有参与者不诚实的可能性来增强安全性,因为仪式只需要一个诚实的参与者即可确保安全设置。这是因为,如果一个参与者销毁他们的随机值,则组合秘密无法被重建。
- Powers of Tau:这些用于 SNARKs,如 Groth16 和 PLONK,通过 MPC 过程提供 SRS。
- Powers of Tau 的概念是生成一个隐藏在加密组中的秘密值 τ(tau)一系列幂的序列(如 g, gτ, gτ²,…, gτᵈ),其中 g 是该组的生成元,d 是参数,表示度数。这些值也是 SRS 的一种,可以在不同电路间重用!
- 多项式承诺:多项式被承诺,以确保其系数被隐藏。承诺是利用 Powers of Tau 仪式中的 SRS 导出的加密对象,并在由验证者随机选择的特定点进行评估——这就是所谓的 挑战。
可信设置的示例:
Groth16 信任设置:
Groth16 使用一个两阶段的设置过程:
- Powers of Tau 阶段:创建一个给定大小电路的通用 SRS。该阶段不是针对特定电路。它基于随机值 τ 生成一组椭圆曲线点。该阶段的输出可以重用于符合一定大小限制的多个电路,限制由τ的最高幂的度数确定。
- 电路特定: 第一阶段生成的参数与电路的 R1CS 表示中的多项式相结合,生成电路特定的密钥:
- 证明密钥(PK):由证明者用于生成证明。
- 验证密钥(VK):由验证者用于验证证明。
- 此设置涉及创建某些与电路约束对应的群元素(椭圆曲线上的点)。每个电路需要新的可信设置,因为生成的参数编码了该电路的确切计算。
PLONK 可信设置:
- PLONK 使用一个 通用且可更新的 SRS,该 SRS 是通过 Powers of Tau 仪式生成的。这允许多个电路共享相同的设置,提供电路在最大必需条件的限制之内的情况下。PLONK 中的 多项式承诺使用 Powers of Tau 对电路约束进行承诺和验证。最常见的多项式承诺方案是 KZG 承诺方案。 这通过将多项式与 tau 的屈指相结合来工作,然后承诺在特定点进行评估。
零知识证明如何在实践中工作
创建零知识证明
实际的 ZKP 系统由前端和后端组成。前端是用于数学上表示问题的约束系统。后端是生成和验证基于电路的证明的证明系统。
要创建一个零知识证明,请从计算问题开始。然后按照以下步骤创建和验证零知识证明:
- 算术化:将计算问题转换为 数学形式(例如,一个约束系统),以便证明系统可以使用。这个算术化问题的形式被称为电路:电路是一组数学表达式(例如,x>5),称为克制,与见证必须满足。
- 证明创建:利用电路生成证明。证明者将他们的知识(见证)编码到证明中而不透露它。这使得证明者能够证明其对已算术化问题的解决方案的知识,而不透露实际值。
- 验证:验证者检查证明以确保有效性,并确认证明者必须知道正确的值。
特定领域语言(DSL)(例如 Noir、Cairo、Circom):
- 为了简化电路编写和验证过程,开发者使用 Noir、Cairo 或 Circom 等语言编写电路。
中间表示(例如 ACIR)和约束系统(例如 R1CS):
- 对于 Noir 或 Cairo 等语言,高级代码编译为中间表示,如 ACIR(算术电路中间表示),将电路逻辑抽象为标准格式,以便后续由各种 ZK 证明后端进行处理。
- 然而,在 Circom 的情况下,电路直接编译为 R1CS,表示需要满足的约束。
证明后端:
证明后端处理电路表示,无论是 ACIR、R1CS 还是其他,并生成加密证明。后端还验证证明(或创建一个智能合约来在链上验证证明),证明计算已正确执行而不泄露任何潜在数据。
- 电路处理:
- 证明后端根据其实现的具体约束系统的规则解释电路。
- 证明生成:
- 后端根据电路和提供的输入生成一个零知识证明。该证明表明某些计算已正确执行而无需泄露潜在数据。
- 证明验证:
- 后端还包括验证给定证明是否有效的机制。
- 验证涉及检查证明是否符合电路规则。
部署:
- 验证者(这只是一个可以验证证明的智能合约)可以在链上部署,这意味着证明可以在链上进行验证。
总结
零知识证明(ZKP)使一个方可以证明对信息的了解,而不泄露信息本身,从而增强区块链应用中的隐私和安全性,并提供构建隐私应用的工具。本文探讨了 ZKP 的工作原理,包括证明者和验证者的角色。它提供了一份简明概述,以帮助开发者了解 ZKP 的概念以及它们在实际应用中的工作原理。
- 原文链接: cyfrin.io/blog/what-is-a...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- ZK编年史:哈希登场 78 浏览
- Layer Zero 发布 Zero 链:去中心化的多核世界计算机 307 浏览
- “Jolt Inside” - 构建者需要了解的全新武器 256 浏览
- 以太坊的下一个重大转变:从重新执行每笔交易到验证 ZK 证明 335 浏览
- Zcash:比特币遗忘的隐私 410 浏览
- ZK编年史:计算模型 284 浏览
- lambdaworks 2026 年更新路线图和优先级 339 浏览
- Lean 4 工程化入门:Elan 工具链配置与 Lake 包管理实战 551 浏览
- 2026年构建机构级DeFi平台真正需要什么 831 浏览
- zkMesh:2026年1月回顾 428 浏览
- 如果它能编译,那它就是正确的(几乎):Lean 4 在 ZK 系统和工程中的介绍 609 浏览
- Zcash 的时代到来了 724 浏览

