Stwo中的递归证明：第一部分

在本文中，我们讨论如何在StarkWare的新零知识证明系统Stwo中实现递归证明验证。通过添加递归证明验证，Stwo可以验证“无限”计算，并为开发人员提供了提供者和验证者效率之间灵活选择的机会。我们的最终目标是使验证者的效率足够高，以便Bitcoin可以使用OP_CAT进行验证，从而将STARK验证引入比特币。该工作是与我们的联营伙伴StarkWare合作完成的。

递归证明

在定义递归证明之前，我们想先介绍在生产中部署零知识证明的三个挑战。

第一个挑战是大型计算证明生成的内存限制。 在生成零知识证明时，计算越大，所需的内存量也越大，可能高达256GB或512GB，这使得在大多数消费者机器上或甚至一些云实例中都无法实现。

当涉及到zkRollup时，这成为一个严重的问题，因为它通常运行一个处理几个区块的zkVM。由于每个区块可能有很多交易，而每个交易可能消耗大量Gas，从而变得计算密集，整体计算会迅速累计并可以达到几个TB。很难找到具有如此大内存的机器来一次性生成zkVM证明。

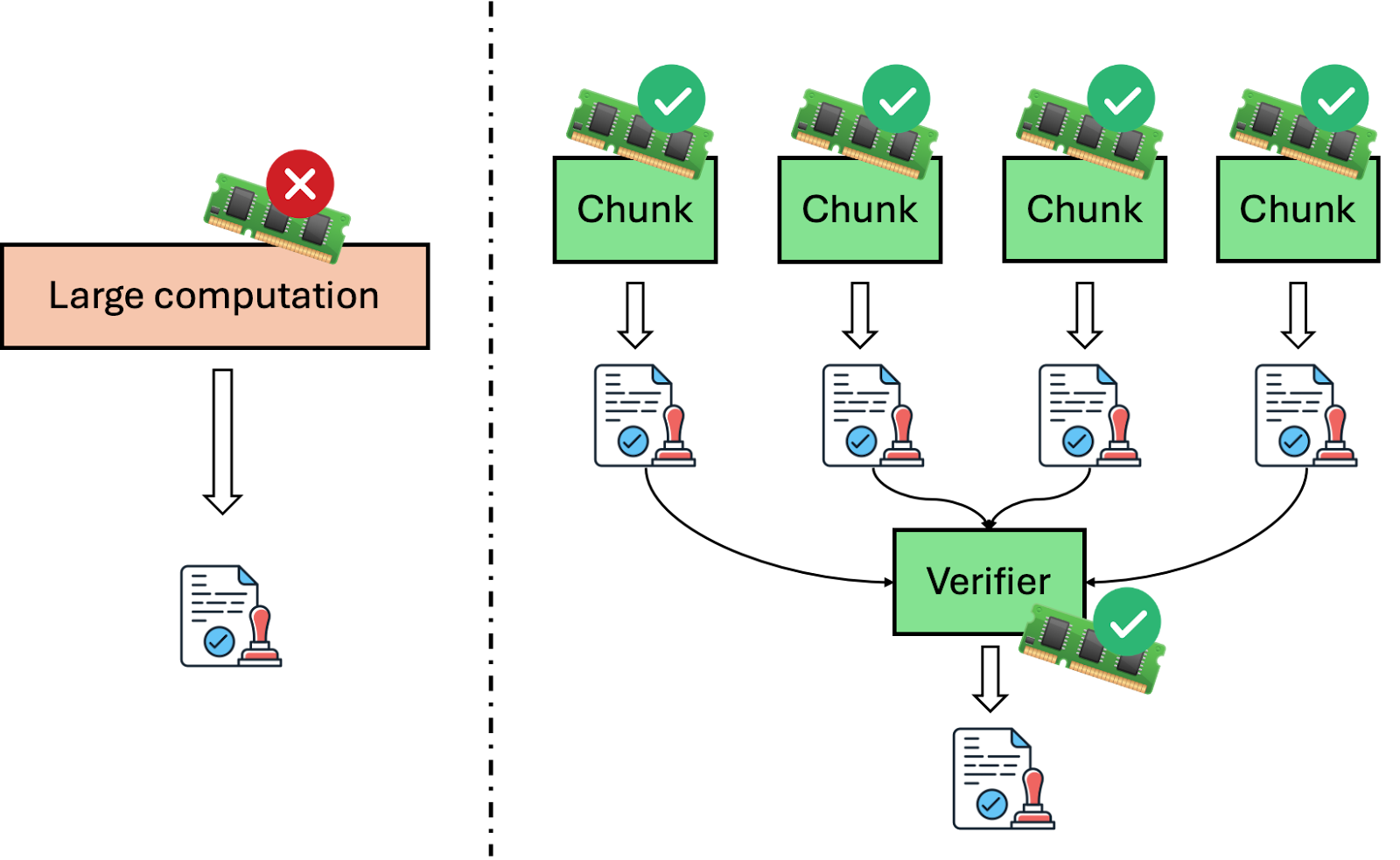
递归证明可以通过将计算切割成可以符合内存限制的小块来帮助解决此问题，并为计算的每一部分生成证明。在上面的示例中，我们将计算切割成四个块，并创建四个独立的证明。

验证者可以选择单独验证这四个证明，并检查计算是否正确切分，但这意味着验证者需要接收更多数据并进行更多工作来验证这些证明。

对于像以太坊或比特币的OP_CAT这种链上证明验证，我们希望最小化验证者的开销，因此我们有另一步骤创建一个证明，目的是将这四个证明合并在一起。具体来说，它证明：

我知道四个证明，每个证明都是有效的，它们是更大计算的正确切片。

这使得验证者只需验证一个证明，而这个证明可以比每个四个证明都要小且更容易被验证，前提是我们正确配置证明系统（这里指Stwo）。更重要的是，尽管进行递归验证意味着需要生成额外的证明，但它们往往是小证明，仅占整体证明生成时间的一小部分。

总之，有些情况下，单次和单个证明中证明非常大的计算是不可行的。将计算切割成小块并使用递归证明验证将它们组合在一起可以解决这个挑战。

第二个挑战是并行和分布式证明生成。 这对zkRollup尤其有用，因为即便在AWS中可用的最大机器也只有192个vCPU，即使拥有一个高效的证明系统，生成证明仍可能需要很多时间，而对于zkRollup，这将导致结算延迟。

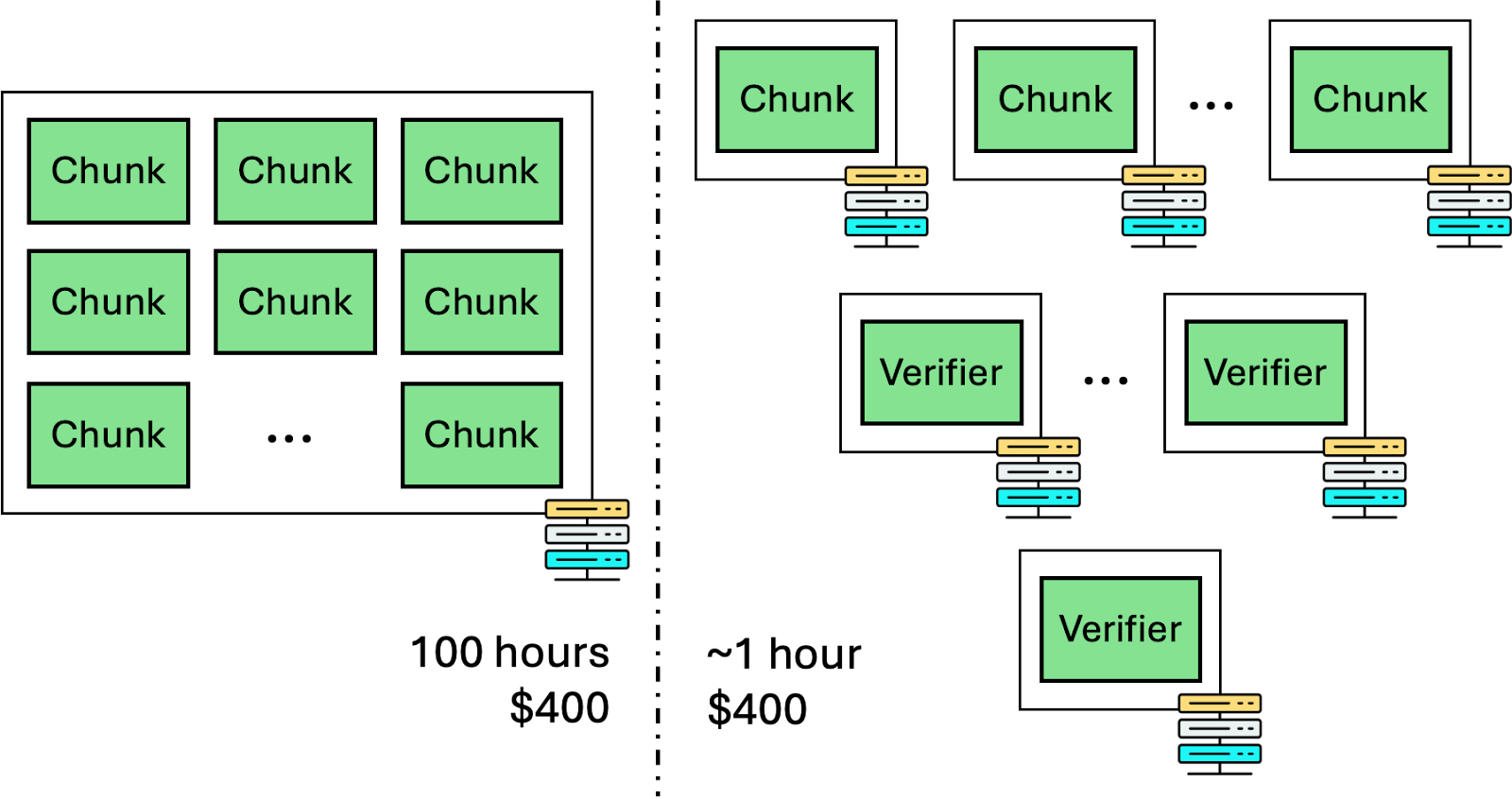
然而，通过递归证明验证，可以大大缩短延迟。假设我有一些计算，预计一个机器需要100小时。我可以将其切分为100个块，预计每个块耗时一小时。现在，如果我有100台机器，我可以在它们之间分配证明生成，如下所示：

• 让这100台机器中的每一台证明一个块。这需要一小时完成。

• 现在，关闭90台机器，仅用10台机器。每台机器使用递归验证将10个证明合并为一个。这大约需要1分钟。

• 关闭9台机器，保持1台机器。该机器使用递归验证将这10个证明合并为一个，青再需要一分钟。

通过这种方式，我们在一小时加两分钟内生成了证明，而不是100小时，这得益于能够在多台机器之间分配递归证明生成的能力。使用云服务器的好处在于可以几乎任意地进行横向扩展和缩减。数学的魔力在于租用云实例进行100小时的计算费用与租用100个云实例每个进行一小时的费用相似，因此使用递归证明并不会增加成本。

第三个挑战是证明者效率与验证者效率之间的斗争。 这对zkVM和zkEVM尤其是一个问题，因为为了使证明生成有效，VM具有许多特定于应用的组件。例如，zkEVM通常在证明系统中为Keccak256和椭圆曲线拥有定制的组件。这些特殊组件是必不可少的，但它们会导致链上验证开销（需要支付$ETH）。

CairoVM及其“builtins”是一个例子，这些是在证明系统中负责某些计算的特殊定制组件。作为行业内第一个zkVM，这些在CairoVM中的设计被许多后来的zkVM或zkEVM所继承。StarkWare在文章"Builtins and Dynamic Layouts"中分享了一些关于builtins如何提高证明者效率的基准数据。

• 使用builtins，Pedersen证明的速度是100倍。

• 使用builtins，Poseidon证明的速度是54倍。

• 使用builtins，Keccak证明的速度是7倍。

• 使用builtins，EC_OP证明的速度是83倍。

然而，使用builtins也有一个代价，即验证者效率会降低。要理解为什么现代证明系统会出现这种情况，我们需要更深入地了解证明者效率和验证者效率的样子。

在现代证明系统中，待证明的计算通常被组织/翻译成一个包含行和列的表格，基本上是一个电子表格。列通常被组织为组，并负责不同的功能。builtins通常实现为一组新列。

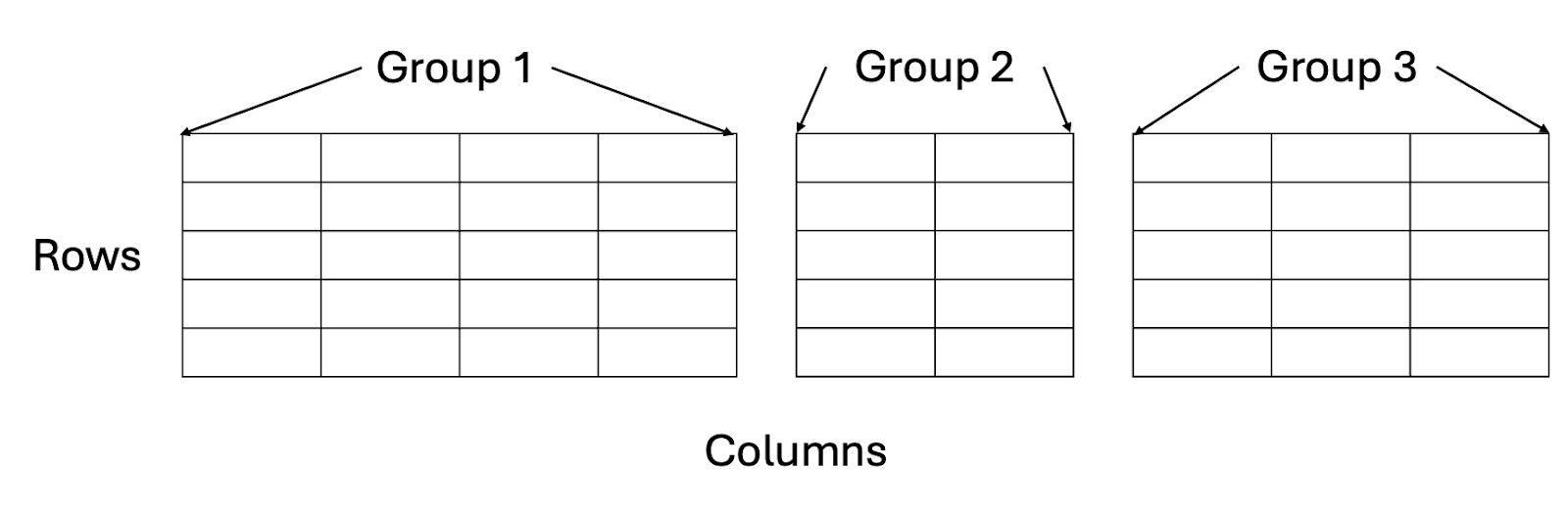
证明系统定义表中单元格之间的一些关系。例如，

• 我们可以强制每行的第一个列（比如说列A）为0或1。

  • 对于每一行i，Ai = 0或1。即Aa * (Ai - 1) = 0

• 我们可以强制第三列（假设是列C）等于第一列和第二列（即加法）（例如列A和B）的和。

  • 对于每一行i，Ci = Ai + Bi

• 我们可以强制第四列（假设是列D）等于前一行的第三列（假设是列C）。

  • 对于每一行i，Di = C{i-1}

这些只是简单的关系。当我们处理像Keccak256或SHA256这样的哈希函数时，它可能由数百列和一长列这样的算术关系组成。

这个表是如何与证明者效率和验证者效率相关的呢？假设该表有X行和Y列。

• 生成证明时证明者的工作主要与表中单元格的数量相关，即X * Y，行数乘以列数。

• 验证者验证证明时所需的工作与列数线性相关，但仅与行数的对数相关，即Y * log(X)。具体来说，验证者的工作与所有需要检查的算术关系的复杂性相关。

buildins对证明者效率有效，因为虽然它们增加了列数，但单元格的净总数量显著减少。然而，这通常会导致验证者开销的增加，仅仅是因为有更多的列并且列之间的关系变得更加复杂。

递归证明验证帮助解决了这个问题。其想法是，对于足够大的计算，如果我们使用两种证明系统的混合，总是“更好”：

• 第一个证明系统针对证明者效率进行了优化，具有适度的验证者效率。第一套证明系统的证明不会在链上进行验证。

• 第二个证明系统针对验证者效率进行了优化，并专门为验证第一套证明系统的证明而设计。该第二套证明系统的证明将在链上进行验证。

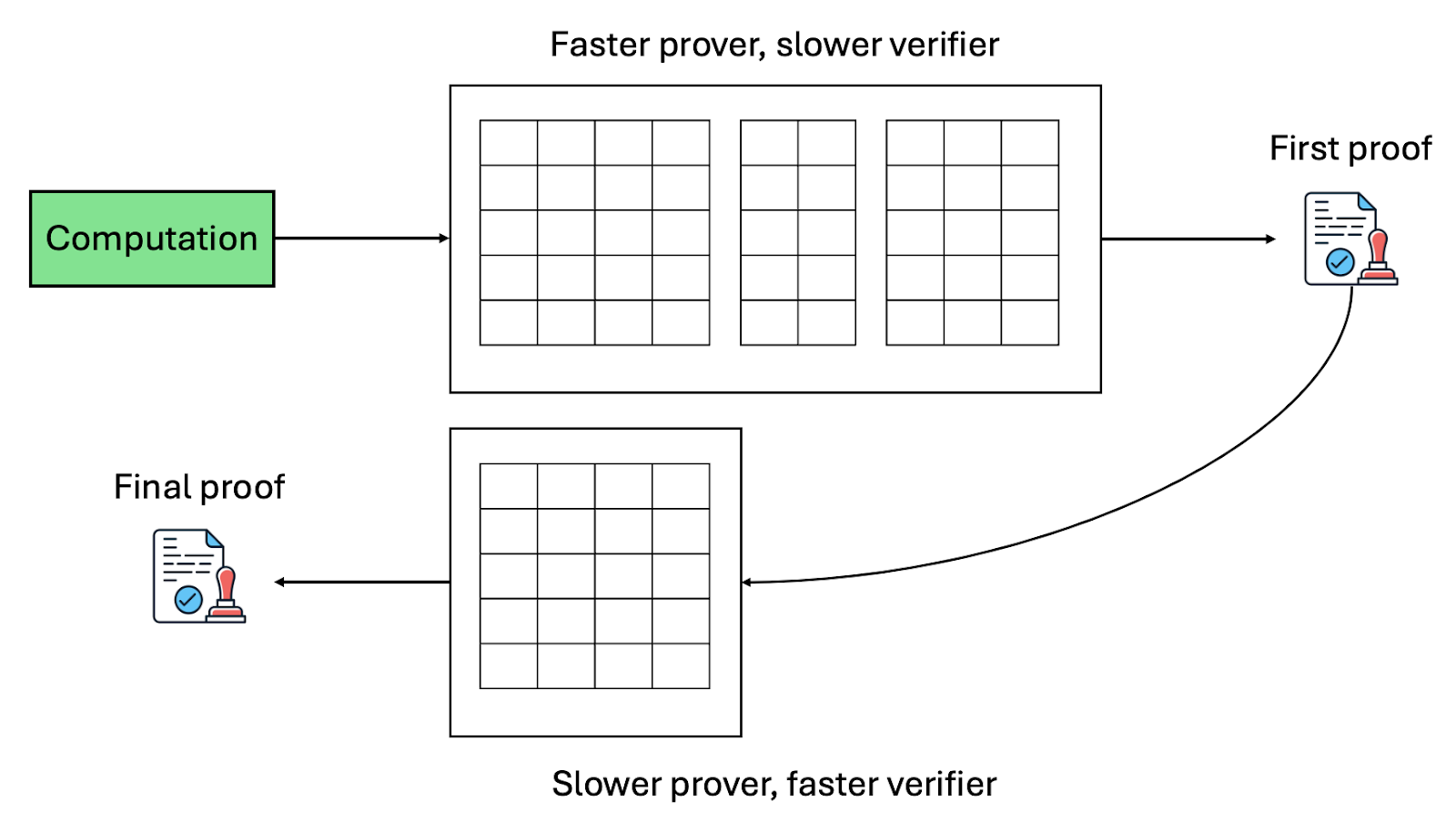
请注意，除了需要设计两个证明系统以满足此目的外，实际上不会从使用两个证明系统中获得任何缺点。这样可以同时改善证明者效率和验证者效率。这一思想最初出自麻省理工学院的Madars Virza，称为zk-SHARKs，自2019年起演变为一种标准做法。

在Stwo中设计递归证明

在递归证明中，核心任务是构建一个用于验证Stwo证明的证明系统（即运行Stwo验证者的计算）。

设计这个专用证明系统并不是一件简单的事情，因为一个粗略的实现很容易得出递归证明的大于原始证明的结果，从而使最终证明“更难被验证”。这在基于哈希的证明系统中尤其如此，因为哈希函数在ZK证明中往往验证成本很高。

在选择哈希函数时有灵活性。Stwo可以与许多哈希函数一起工作：Blake2s、Blake3、Poseidon2和SHA-256。在这些哈希函数中，Poseidon2是最容易验证的，但在一个没有Poseidon2内置功能的粗糙证明系统中运行Poseidon2会显得低效。

因此，我们在Stwo上构建了一个专用的证明系统，专门用于验证Stwo证明。它由两个组件组成：（1）Plonk和（2）Poseidon。Stwo验证者的大部分逻辑是在Plonk中实现的，但每当验证者需要计算Poseidon2哈希时，它会将其委派给Poseidon组件。这两个组件通过Ulrich Haböck的LogUp校验和相互连接。

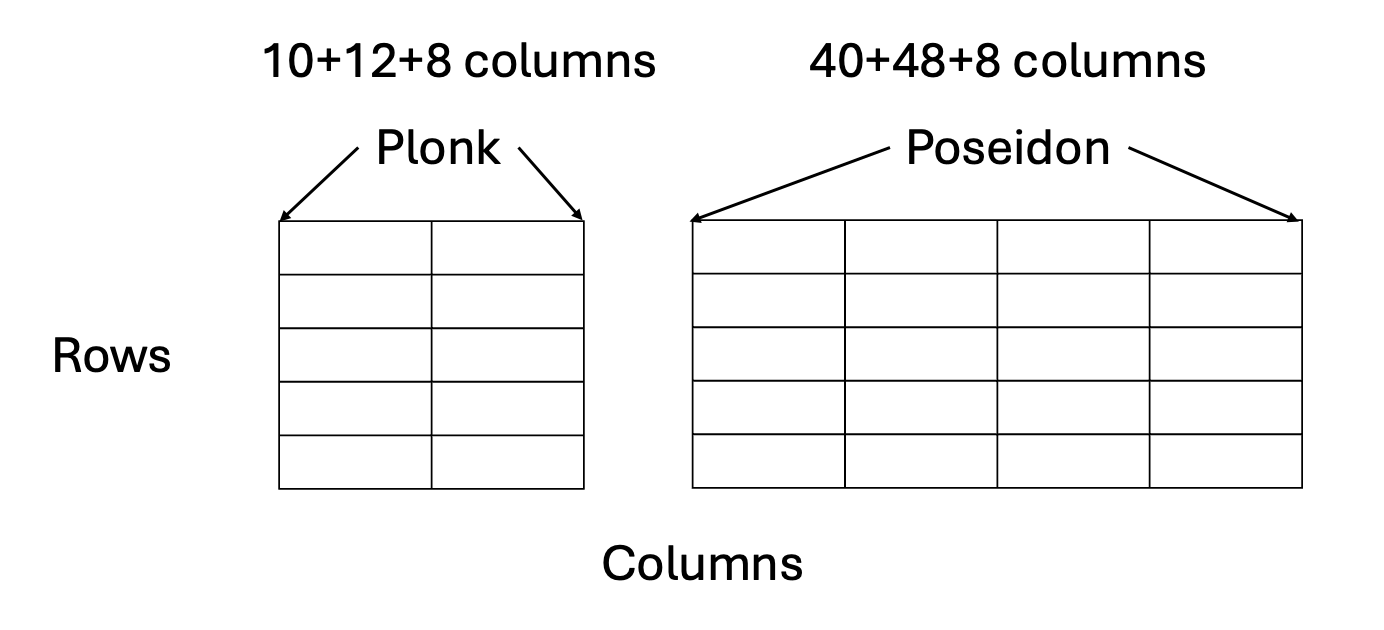
我们相信这是一个相当整洁且制作良好的设计，我们将在后面展示它提供了良好的性能。在这系列文章中，我们旨在为你提供这些组件的详细信息。让我们开始吧！

Plonk组件有10 + 12 + 8列：

• 前10列称为“预处理”列。这些是Stwo验证者的描述，不依赖于证明，因此证明者只需计算一次，而无需再次计算。它们的列表如下：“a_wire”、“b_wire”、“c_wire”、“op”、“mult_a”、“mult_b”、“mult_c”、“poseidon_wire”、“mult_poseidon”、“enforce_c_m31”。我们很快会解释它们的含义。

• 接下来的12列称为“迹”列。每4列代表M31域元素的度-4扩展，其中M31指的是模梅森素数2^31 - 1的数字。这是Stwo验证者中的基本计算单元。因此，这12列代表三个这样的数字，称为“a_val”、“b_val”、“c_val”。我们随后会讨论它们的含义，但Stwo验证者的计算是基于该度-4扩展的。

• 最后8列用于LogUp校验和，将Plonk组件中的不同行连接在一起，并将Plonk组件与Poseidon组件连接起来。

Poseidon组件有40 + 48 + 8列：

• 前40列也是“预处理”列。它们与哈希函数的输入和输出无关，而是提供一些描述。

  • 其开头有四列“is_first_round”、“is_last_round”、“is_full_round”、“round_id”，描述这一行是否对应Poseidon2哈希函数中的第一轮、最后一轮和/或完整一轮，以及轮次数标识。

  • 后面是32列用于Poseidon2哈希函数的轮常数。

  • 最后有四列“external_idx_1”、“external_idx_2”、“is_external_idx_1_nonzero”、“is_external_idx_2_nonzero”，指示Plonk组件中的哪一行应对应这一行——将两个组件连接在一起。

• 接下来的48列为“迹”列。它包含三个Poseidon2状态（每个状态有16个元素），一个作为输入状态，一个作为中间状态，一个作为输出状态。

• 最后8列同样用于LogUp校验和。

在本文中，我们将重点关注Plonk组件，并讨论它是如何工作的，以及我们为什么以这种方式设计它。在第二部分文章中，我们将更详细地讨论Poseidon组件。在第三部分文章中，我们将专注于如何构建一个兼容比特币验证者的证明系统，这涉及一些仅对比特币相关的详细内容。

A、B、C之间的算术关系

我们从Plonk组件中最直观的部分开始。这涉及到一个预处理列“op”和12个追踪列，形成度-4扩展“a_val”、“b_val”和“c_val”。

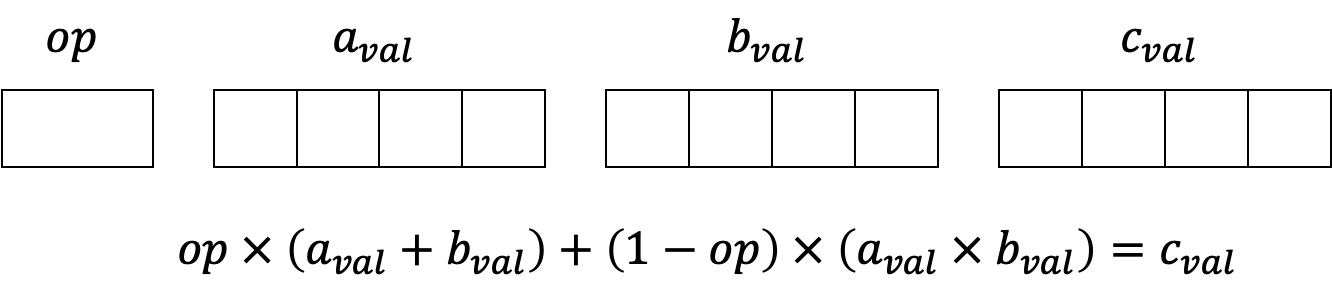
然后可以用来定义这些值之间的加法和乘法关系。

• 当op = 1时，我们有C = A + B

• 当op = 0时，我们有C = A * B

• 当B = 0时，我们有C = op * A，这可以看作是将A乘以一个与证明无关的常量op

通过加法和乘法，可以执行其余的算术运算。

• 像A - B的减法可以通过先将被减数B乘以-1再将A和(-B)相加来实现。

• 在素数域A / B的除法通常定义为A * (B^-1)，其中B^-1是B的乘法逆元素，例如B * (B^-1) = 1。这是通过提供模逆，使用B * (B^-1) = 1来检查它是否是正确的模逆，然后与A相乘来完成的。

但是，这个简单关系存在两个问题。

我们首先从较简单的问题开始。请注意，A、B、C都是M31域的度-4扩展，称为QM31。QM31中的一个元素可以类似于复数写为：

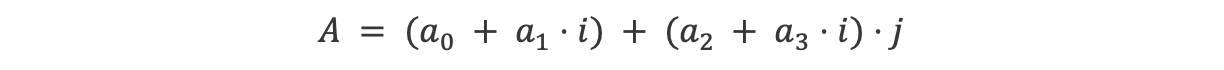
其中i和j是单位。A也可以视为向量[a0、a1、a2、a3]。

尽管我们可以对QM31执行各种运算，但几乎没有办法强制QM31元素也是M31元素（即a1 = a2 = a3 = 0）。然而，在Stwo验证器中，这是必要的，因为某些元素应该是M31而不是QM31。

为此，我们有另一列“enforce_m31”，该列强制C为M31，这意味着代表“c_val”的第二、第三和第四列应该为零。

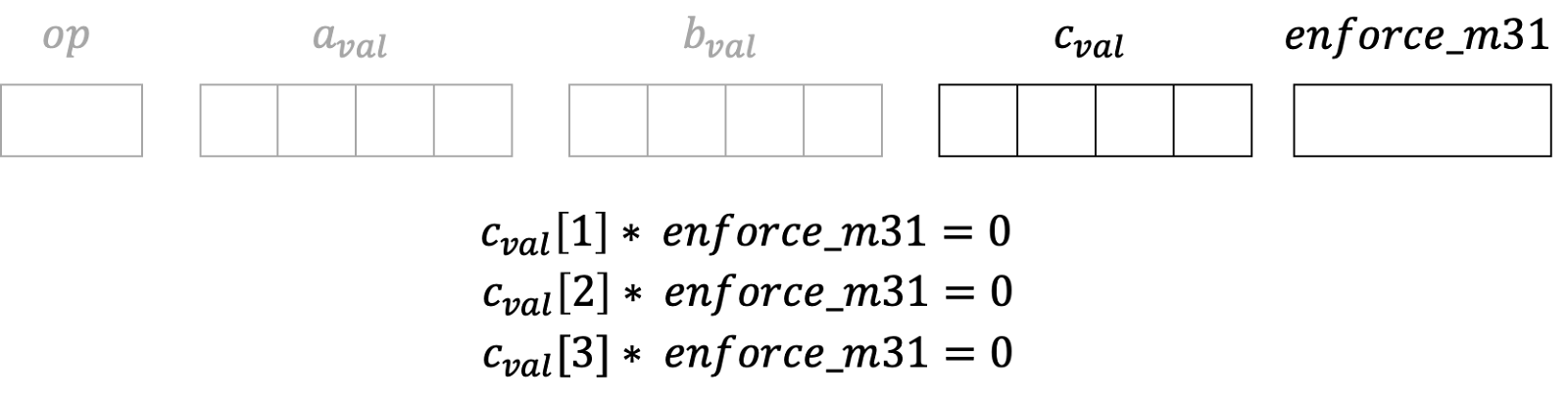
尽管“enforce_m31”仅强制C，但我们很快会展示如何以间接方式强制A和B为M31元素。这正是另一个问题。

如你所见，虽然我们可以在一行中执行单个加法或单个乘法，但为了能够容纳更复杂的计算，即使是减法和除法，我们将需要多于一行，其中一行中的结果C可能成为另一行的输入A。

但此时，我们没有办法强制该行中的C成为另一行中的A。这对于减法是必要的，因为被减数乘以-1需要出现在另一行中才能计算差值。

这就是“wire IDs”发挥作用的地方，对于每一个值，我们分配一个ID。来自同一ID的值，无论是在同一行还是不同的行中，都必须保持相同。通过这种方式，不同的行可以连接在一起。

因此，如下图所示，在每行中，现在有三列预处理列“a_wire”、“b_wire”、“c_wire”。它们是A、B和C的相应wire ID。

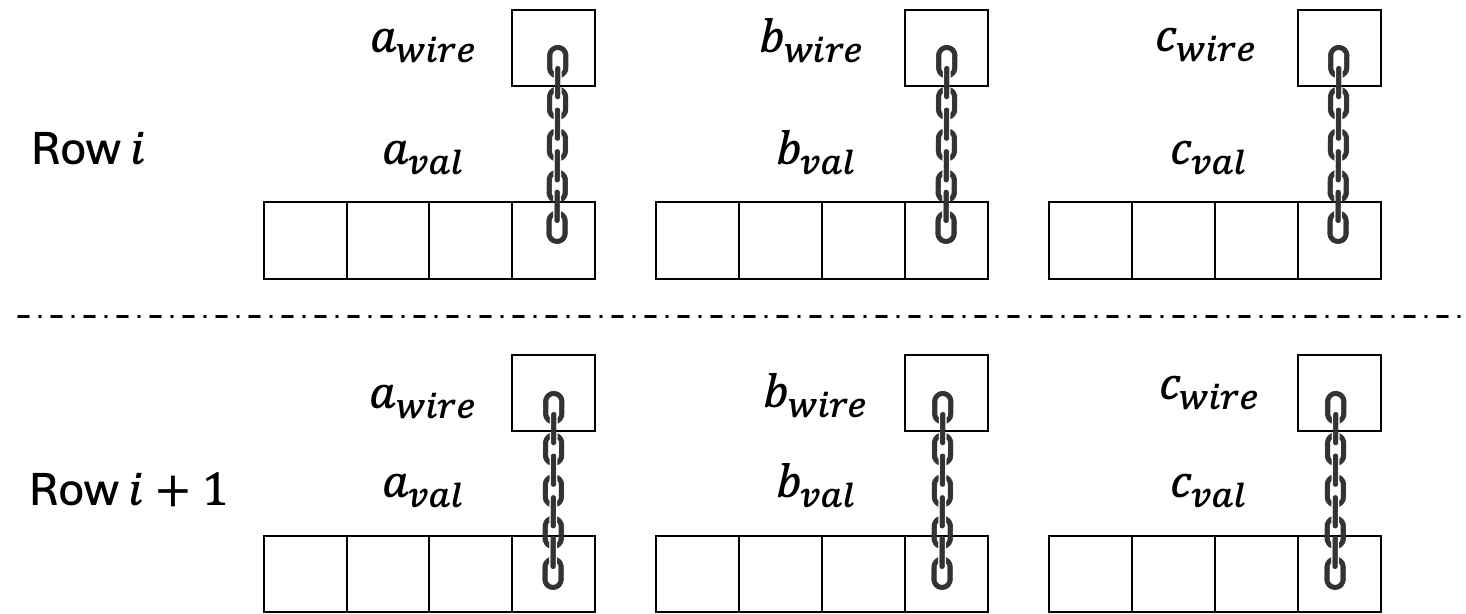
具有相同ID的值，它们可以在同一行或不同的行中，必须具有相同的值，因此现在一行可以“继续”另一行未完成的计算。确保相同ID的值必须相同是通过LogUp技术来强制执行的如下。

使用LogUp连接跨行的值

LogUp是Ulrich Haböck在2022年提出的一种技术，可以用来连接表中不同行的值（及其ID）。

其思路是，如果所有值和ID一致，我们可以为每行推导出“mult_a”、“mult_b”、“mult_c”，使其满足以下方程。

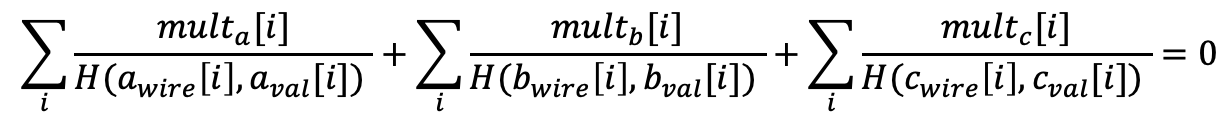
在这个方程中，H是由验证者选定的随机且不可预测的哈希函数。基本上，如果两个输入wire ID和value相同，则该哈希函数将输出相同的数字，但这个数字将是随机的并不能被证明者预测。也就是说，如果两个输入具有相同的wire ID但不同的值，则通过该哈希函数输出的结果将不同，并且证明者无法预测输出之间的差异。

“mult_a”、“mult_b”、“mult_c”可以仅基于“a_wire”、“b_wire”和“c_wire”进行设置。例如，如果一个特定的wire ID在整个表中使用了16次（可能出现在位置A、B或C），我们可以将该wire ID的第一个“mult_X”值设置为“-15”，并将所有其他与该wire ID相关的“mult_X”值设置为“1”。这样一来，在整个表中，所有与此wire ID相关的分数将相加为零。

如果以这种方式正确配置了所有wire ID，则上述的总和也将为零。

现在，如果有任何输入使得wire ID和value不一致，LogUp论文证明，基于哈希函数的不可预测性，和相应的分数将不会为零，这种概率是压倒性的。这种哈希函数可以由两个随机变量“α”和“z”具体构造，这两个变量在证明者提交所有迹列后由验证者选择。

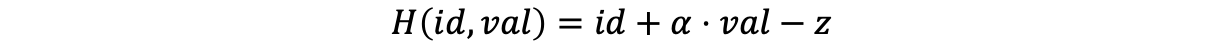
为了计算整个表的校验和，还使用了8更多的列来聚合总和，每4列代表中间聚合结果。我们将它们称为“sum_1”和“sum_2”。

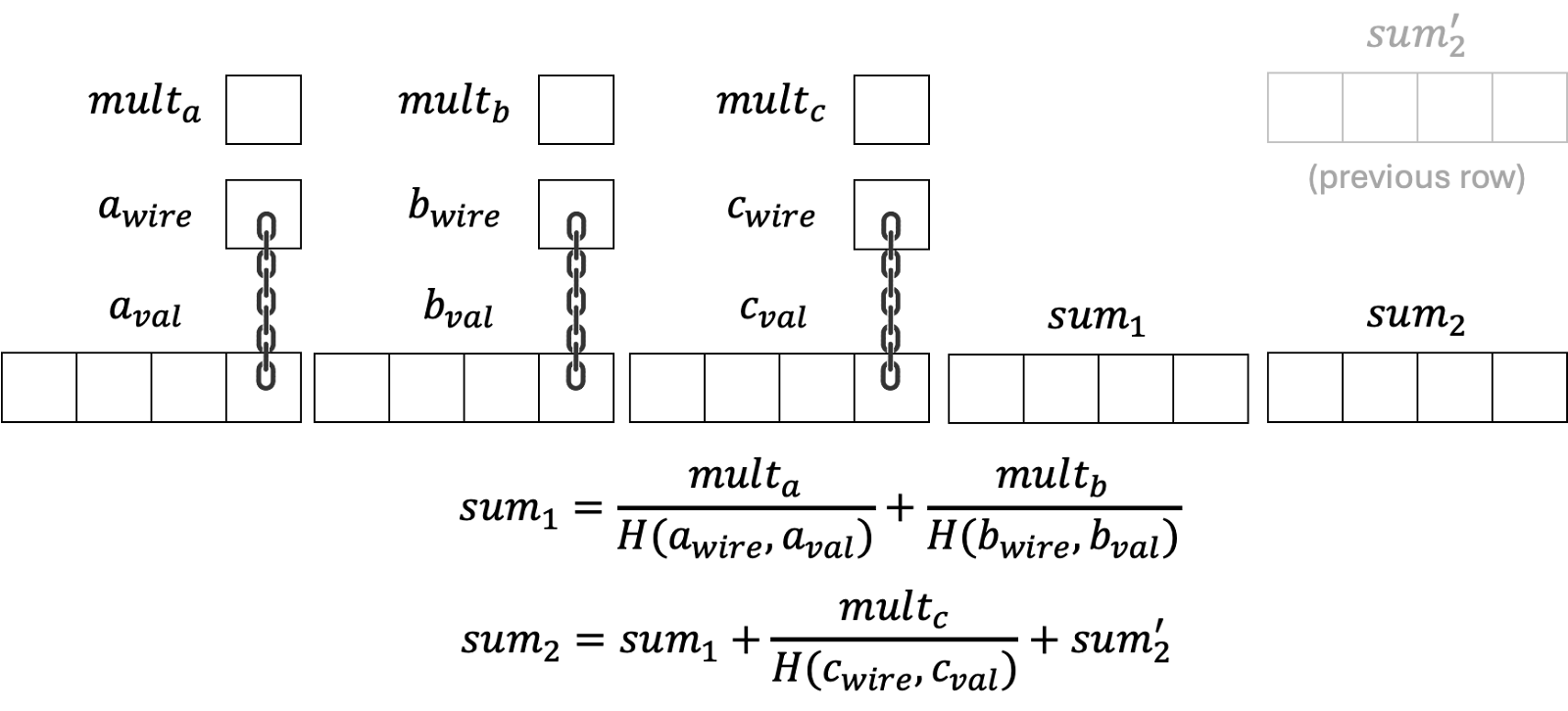
如图所示，“sum_1”只是A和B的分数之和，而“sum_2”将C的分数和上一行的“sum_2”相加到“sum_1”中。LogUp技术巧妙地利用了一个技巧，在Circle STARK中，第一个表的每一行的上一行被“定义”为该表的最后一行，因此第一行也将添加该表最后一行的“sum_2”。可以证明，如果“sum_2”关系即使以这种循环方式也能得到满足，那么所有行中A、B、C的分数之和为零。以下是一个例子，其中第一行有sum_2[0]，最后一行有sum_2[7]。sum_2[0]的计算将涉及sum_2[7]，但sum_2[7]也取决于sum_2[0]。只有在总和为零时，这才会发生。

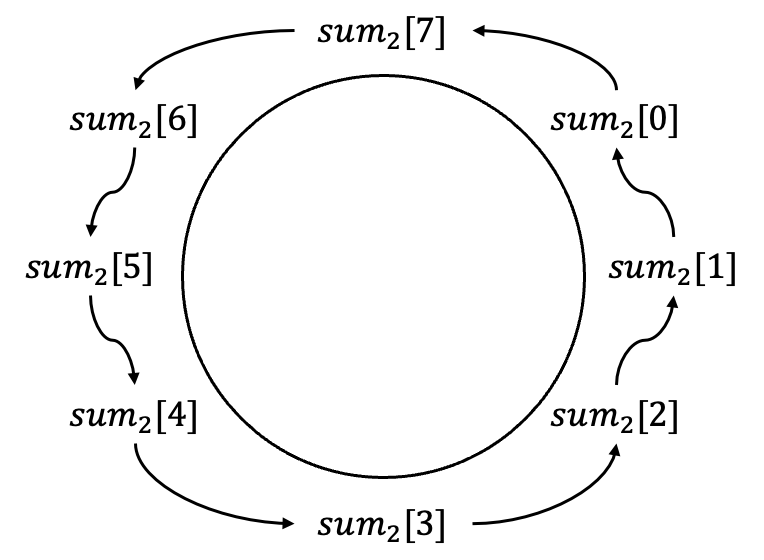
请注意，还有“poseidon_wire”和“mult_poseidon”将在“sum_2”中涉及，我们此处暂时省略。它们用于确保Plonk组件与Poseidon组件之间共享值的一致性，我们将在第二部分讨论该内容。

下一步

在本文中，我们介绍了Plonk组件的设计细节，其设计可以总结为两个部分。一部分处理三值A、B和C在一行内的基本算术运算（加法和乘法），另一部分利用LogUp技术维护跨行保持相同ID值之间的一致性。

在下一篇文章中，我们将深入讨论Poseidon组件的设计以及它如何与Plonk组件交互。在介绍完这两个组件后，我们将展示如何在这两个组件内实现递归验证者。

在l2iterative.com和推特@l2iterative找到L2IV。

• 原文链接： l2ivresearch.substack.co...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～