区块链中的数学-SM2的签名和验证过程

写在前面

上一节说了sm2与KDF密钥导出函数并且整理20-30篇目录。KDF在密码学中用途很多，当然不局限sm2.

本文详细说说sm2的签名和验证过程。

sm2签名过程

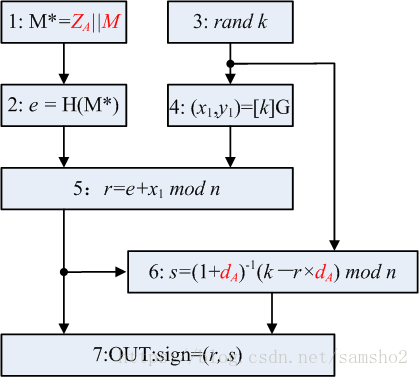
假设用户A作为签名者，拥有长度为$entlen_A$比特的可辨别标识$ID_A$，私钥$d_A$, 公钥$P_A=(x_A,y_A)$ , 待签名的消息为M 。

预计算出 $Z_A=H_{256}(entlen_A \| ID_A \|a \|b \|G_x \|G_y \|x_A \| y_A)$

1. 计算 $M^*=Z_A \|M$
2. 计算 $e=H_v(M^*)$，按规则将e的数据类型转换为整数；
3. 产生随机数$k \in [1,n-1]$
4. 计算椭圆曲线点$(x_1,y_1)=KG$，按规则将$x_1$的数据类型转换为整数；
5. 计算 $r=(e+x_1)\ mod\ n$，若r = 0或 r + k = n则返回3；
6. 计算 $s=((1+d_A)^{-1} * (k-r * d_A))\ mod\ n$，若 s = 0则返回3；
7. 按规则将r、s的数据类型转换为字节串，得到消息M的签名为(r,s)。
   [注：按sm2的曲线参数，则r和s分别为32字节，即签名值为64字节]

在签名的时候，如果不指定用户身份标识ID参数，该参数是有默认值的。默认值为

0x31 0x32 0x33 0x34 0x35 0x36 0x37 0x38 0x31 0x32 0x33 0x34 0x35 0x36 0x37 0x38

流程图可表示如下：

sm2验证签名

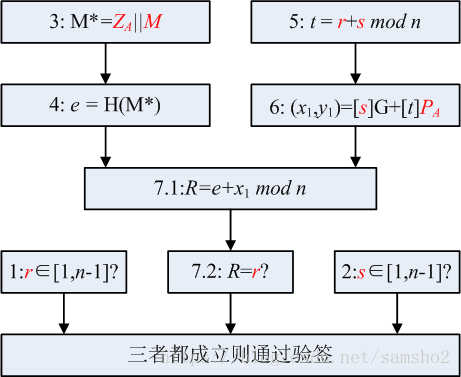
作为验证者的用户B，为了检验收到的消息M及其数字签名(r, s)，执行以下步骤：

1. 检验 $r \in [1,n-1]$，若不成立则验证不通过；
2. 检验 $s \in [1,n-1]$是否成立，不成立当然也不通过
3. 计算 $M^* =Z_A \| M$；
4. 计算$e = H_v(M^∗)$，按规则将e的数据类型转换为整数；
5. 计算$t = (r + s) mod\ n$，若t = 0，则验证不通过；
6. 计算椭圆曲线点$(x_1,y_1)= [s]G +[t]P_A$
7. 按规则将$x_1$的数据类型转换为整数，计算$R = (e + x_1) mod\ n$，检验 R = r 是否成立，若成立则验证通过；否则验证不通过。

[注：$H_v$表示消息摘要长度为v比特的杂凑算法或者哈希算法，没什么特别之处]
流程图可表示如下：

凡事多问个为什么总是好习惯，为什么可以这样来验证？

验签原理

验证的关键是验签步骤计算的点$(x_1,y_1)$ 等于签名步骤中产生的点 $(x_1,y_1)$
看下具体推导：
$sG +tP_A=sG+sP_A+rP_A$
$=sG +sd_AG +r * d_AG$
$=(1+d_A) \times sG +r * d_AG$
$=(k-r * d_A)G +r * d_AG$
$=KG=(x_1,y_1)$

所以R == r

可以看到整个过程与secp256k1签名和验证过程较为相似，关于后者可在本文最后相关阅读中找到。

小结

本节讲了SM2签名算法，总体过程与secp256k1签名过程类似，不难理解，没有举例子说明，感兴趣的朋友自己选取数据实际操练一下。

本文内容主要参照 《《GBT 32918.2-2016 信息安全技术 SM2椭圆曲线公钥密码算法 第2部分：数字签名算法》GM/T0009-2012《SM2密码算法使用规范》

好了，下一篇继续说sm2的密钥协商过程。

欢迎关注公众号：blocksight