区块链中的数学 - RSA的选择密文攻击
- blocksight
- 更新于 2020-07-05 21:39
- 阅读 6980
本节主要介绍了RSA的两种攻击方法，重点说了选择密文攻击，并说明了对应的解决方案--最优随机填充（OAEP）。
写在前面
上一节介绍了RSA签名和安全分析，重点说了计时攻击及其防范方法。
本节继续分析后两种攻击方法。
4. 基于硬件故障攻击
5. 选择密文攻击
基于硬件故障分析
该种类型攻击非本文重点，这里只是简单介绍一下此种攻击方法。
“这种攻击的目标是对产生签名的处理器，通过减少处理器的输入电功率，以在签名计算中引入故障。 故障导致软件产生无效签名，然后攻击者通过分析恢复出私钥。 这种攻击并未对RSA造成严重威胁，因为它需要攻击者能够物理接触到目标机器并且能够控制处理器的输入电功耗。”
选择密文攻击
重点说一下选择密文攻击CCA（Chosen Ciphertext Attack）[注：与之对应的有选择明文攻击]：
通常来说，攻击者选择一个明文，用目标对象公钥加密，然后用目标对象解密取回明文，攻击者获得不到什么有用的信息。
但是攻击者可以刻意选取一些数据，利用目标对象解密时获取密码分析的有用信息，这里用到了RSA性质。
利用RSA的性质：
E（PU,M1）* E（PU,M2）=E（PU,[M1M2]）
利用CCA攻击，可以用如下方式解密：
假定一攻击者截获密文 C =$M^e$ mod n，此时无法解密M，但可以执行如下计算：
（1）计算X = C * $2^e$ mod n
（2）将X作为选择明文提交，并收到 Y =$X^d$ mod n
看下面等式： X = C $ 2^e $ mod n = $M^e$ $ 2^e$ mod n = $(2M)^e$ mod n
因此 Y = 2M mod n ，所以可得到消息M
这种攻击利用RSA性质：
<1> E(PU,M1) E(PU,M2) = E(PU,M1M2)
PU是公钥，M是待加密内容。
即:
$(M1)^e$ mod n $(M2)^e$ * mod n = $(M1M2)^e$ mod n
解决办法是在明文加密前先对明文进行随机填充，让密文随机化,从而 式不再成立。 事实证明简单的填充依然具有较低的安全性，下面介绍RSA数据公司推荐的最优非对称加密填充。
最优非对称加密填充
最优非对称加密填充（Optimal Asymmetric Encrypt Padding）简称OAEP。 这个详细过程说来比较复杂，具体实现也可能略有不同。网上有幅流程图对主要过程说的较为清楚，这里引用下：
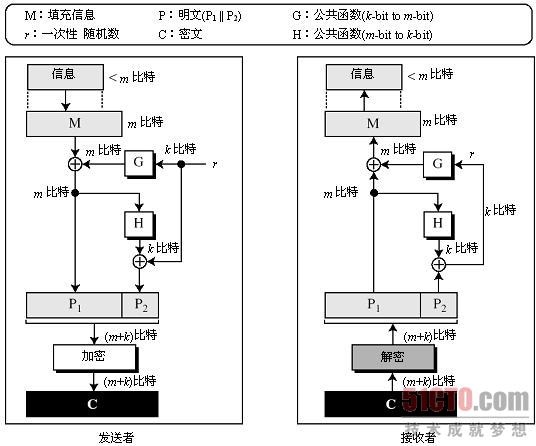
发送者A执行加密过程，接收B执行解密过程。
加密过程：
- 由于RSA是按块来加密的，不足块长度的需要填充特定字符（比如0）.A选择将原始消息填充成一个m比特的信息，称为M。
- 选择一个k位比特长度的随机数r【注：r只用一次】
- 用公共单向函数G【将r比特长度转m比特整数】生成掩模信息：$P1=M\bigoplus G(r)$
- 创建明文 $P2=H(P1)\bigoplus r$ 的第二部分。H是一个加密的散列函数，用一个m比特的输入产生k比特的输出。
- 令P = P1 || P2，A正常加密 $C =P^e mod n =(P1|P2)^e\ mod\ n$ 发送C。
解密过程：
- B正常解密$P = C^d\ mod\ n = P1 | P2$ 。
- 计算$H(P1)\bigoplus P2 = H(P1)\bigoplus H(P1)\bigoplus r = r$ 得到随机数r 。
- 计算 $G(r)P1\bigoplus P1 = G(r)\bigoplus M\bigoplus G(r) = M$, 得到块数据M。
- 从M当中取消填充后，得到原始信息。 具体代码实现可参考OpenSSL 或Java Bouncy Castle 实现。
这样的处理使得明文加上了掩码信息，加强了安全性，同时容易证明解密能够得到加密前的消息M。
小结
本节主要介绍了RSA的两种攻击方法，重点说了选择密文攻击，并说明了对应的解决方案--最优随机填充（OAEP）。 可以看出安全问题就像矛与盾，有了新的矛就得研发新的盾，盾增强了，就会有人发展更强的矛（不一定是攻击者，也可能是安全研究人员）。
关于安全分析，还没有说完，还有一种常见的共模攻击，这种攻击方式本质上属于数学攻击的一种，所以在RSA攻击方式一文中没有单独列出。
另外，本节提到了填充方式，在PKCS（Public-Key Cryptography Standards） 公钥密码学标准中制定了相应的规范，以后找机会单独说明。
好了，下一篇继续说RSA的共模攻击。
欢迎关注公众号：blocksight
